大錨片螺旋錨在粉質黏土中的下壓承載性能

屈訟昭，郭詠華，王儀，張斌，張建明，孫清

(1.河南城建學院 土木與交通工程學院，河南 平頂山 467036；2.中國電建集團河南省電力勘測設計院有限公司，鄭州 450000；3.西安交通大學 人居環境與建筑工程學院，西安 710049)

螺旋錨基礎是一種由螺旋錨和上部承臺等構件組成，主要利用深層土體抵抗上部結構作用的錨固結構體。該基礎以鋼構件為主，施工工序少、施工簡單，可顯著減少或避免使用混凝土材料，從而極大程度上縮短施工周期。同時，螺旋錨施工時不必大范圍開挖，地表破壞范圍相對較小，環保效益明顯，尤其對生態脆弱地區。此外，螺旋錨對土體的擾動小，能充分發揮原狀土體固有強度，實現基礎材料節省。鑒于螺旋錨基礎的上述優點，工程中對其進行了一定的探索性應用[1-2]。2016年，巴西某500 kV雙回線路工程中，針對軟土地基采用單腿7根螺旋錨傾斜布置基礎。在該項工程中，螺旋錨基礎應用300余基，應用率超過50%。2017年，淄博齊林電力設計院有限公司在濟青高鐵朱臺牽引站供電工程(吳磨—朱臺牽引站220 kV線路部分)對3基雙回路直線塔采用螺旋錨基礎，土質以粉質黏土和粉土為主。為了加速推進該基礎在輸電線路工程中的應用，國家電網公司于2018年設定了關于螺旋錨基礎的多個試點工程，包括：平原黏性土地區，山東濰坊官亭(高密)500 kV變電站220 kV送出工程和淄博千乘至蘆湖(至高清)220 kV線路工程；祁連山地草原環境地區，青海海北默勒至祁連110 kV線路工程。

為了對該基礎類型提供理論支撐，較多學者對其受力性能等方面進行了一定的研究。目前，關于螺旋錨基礎承載力的研究主要集中在抗拔性能方面，Demir等[3]對在黏土中的單錨進行室內拉拔試驗，并且基于數值模擬對比分析不同埋深比對多錨片螺旋錨抗拔性能的影響規律。胡偉等[4]通過對處于中砂內的單葉片螺旋錨上拔試驗研究，初步揭示了錨片表面土壓力的分布規律。Wang等[5-7]對處于凍土中的螺旋錨基礎上拔承載力進行了試驗研究和數值分析，闡明螺旋錨幾何尺寸對其抗拔性能的影響規律。張昕[8]詳細歸納螺旋錨基礎在上拔性能方面的研究成果，發現巖土的性質對螺旋錨上拔性能及破壞模式影響很大，并基于對螺旋錨上拔受力過程中周邊土體(砂土)變形場的研究，闡明了螺旋錨上拔破壞的力學機理，建立了螺旋錨抗拔承載力計算模型，提出砂土中螺旋單錨上拔承載力的計算方法。而在實際工程中，螺旋錨除了承受上拔荷載之外，還要承受較大的豎向荷載。王希云[9]、邵康等[10]對砂質土地區中的三盤螺旋錨進行了豎向抗壓承載力試驗研究和數值模擬分析，論證了確定螺旋錨承載力取值方法的適用性，揭示了在豎向荷載作用下螺旋錨錨桿側阻、錨片端阻以及錨桿端阻所占的比重，闡明了螺旋錨承載力隨錨盤間距改變的變化趨勢。對于其他土質中螺旋錨的抗壓性能研究報道較少。

上述螺旋錨錨片的最大直徑為300 mm。美國喬斯林公司曾生產螺旋錨葉片最大直徑為395 mm，前蘇聯使用的最大錨片直徑為460 mm，日本九州電力公司在TACSR工程中使用的螺旋錨基礎錨片最大直徑為420 mm。中國目前使用的螺旋錨錨片直徑一般都在360 mm以下[11]。大錨片可以更大程度地提高該類型基礎的承載力，但基于常規錨片提出的承載力判別條件，以及螺旋錨基礎的破壞模式和相關參數對極限承載力的影響規律是否適用，需要進一步研究確定。筆者基于黏性土地區的多葉片大直徑螺旋錨基礎靜載試驗，對比討論現有極限承載力判別條件的適用性；建立螺旋錨基礎精細化有限元模型，通過與現場靜載試驗結果對比，驗證有限元模型的合理性，在此基礎上分析大葉片螺旋錨基礎在豎向壓力作用下錨桿側阻、葉片端阻的荷載分擔規律。

1 試驗場地土層評價

試驗場地在河南省駐馬店市上蔡縣蔡溝鄉，該地區處于淮河沖洪積平原地帶，地貌單一，地形平坦，地勢開闊。現場靜力觸探發現，地層土質較均勻，從地表至31.5 m深度處以粉質黏土為主，黏土狀態為可塑～硬塑，具中壓縮性。土質呈褐黃、褐灰、灰黃等色，含鐵錳氧化物，零星見小鈣質結核與蝸牛殼碎片，夾粉土，其中，地表1.0～2.0 m為耕土，深度14.5～16.5 m范圍內局部為粉土。試驗中錨桿的埋深位于9～12 m，在錨桿的埋深范圍內可以把周圍的土質視為均勻分布的粉質黏土，土層物理性質指標以及力學性質指標見表1。

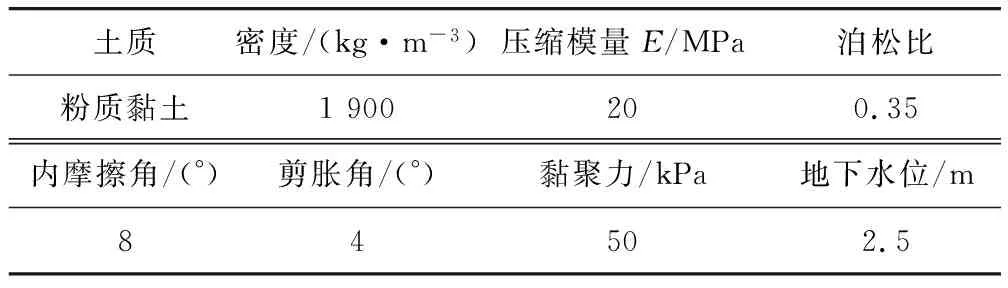
表1 土層物理性質指標以及力學性質指標

2 螺旋錨抗壓靜載試驗與結果分析

2.1 試驗概況

螺旋錨現場原位試驗布置如圖1所示，現場采用塔位處的灌注樁基礎作為反力樁，螺旋錨1、3、5和7分為位于反力樁間約三等分點處。現場將反力梁與灌注樁上的預埋地腳螺栓相連，通過千斤頂向螺旋錨頂部施加壓力，如圖2所示。螺旋錨抗壓靜載試驗采用快速荷載維持法，加載按照每級60 kN依次遞增，每級加載保持10 min，加載至錨桿頂部豎向位移超過40 mm停止，卸載采用相同的方式。試驗中采用壓力表測定千斤頂油壓來換算得到施加的荷載，千斤頂量程為5 000 kN，螺旋錨豎向位移通過安裝在千斤頂下部的位移傳感器測量。

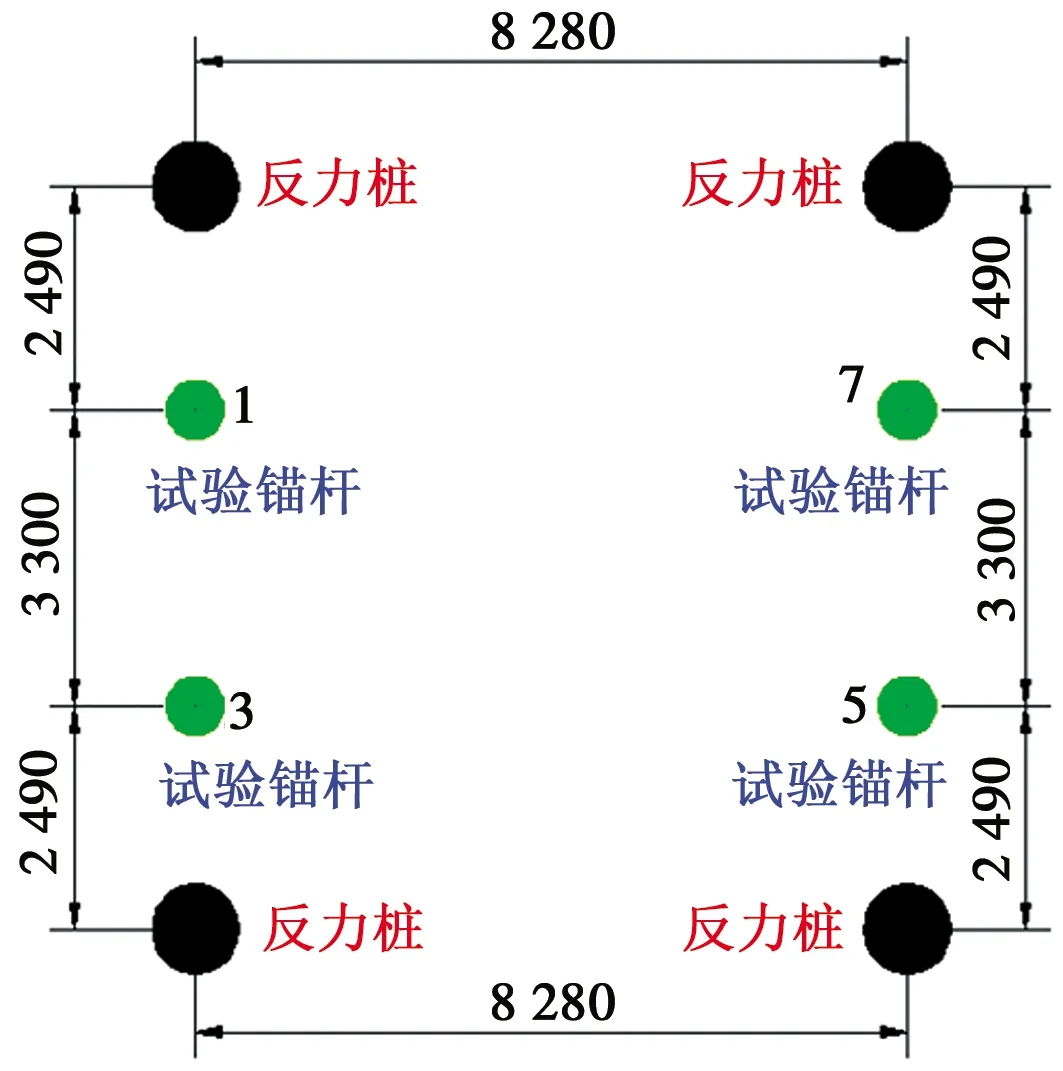
圖1 靜載試驗布置(單位：mm)

圖2 靜載試驗裝置

對4個螺旋錨進行受壓試驗研究，其中1號為埋深9 m的兩盤螺旋錨，具體尺寸如圖3(a)所示。3號為埋深9 m的三盤螺旋錨，具體尺寸如圖3(b)所示。5號為埋深12 m的兩盤螺旋錨，加工尺寸同1號螺旋錨。7號初始設計為埋深12 m的3盤螺旋錨，但在鉆入施工時由于土質較硬，當鉆入約9 m時發現施工困難，現場臨時改為埋深為9 m的三盤螺旋錨。螺旋錨錨盤和錨桿均采用Q345B級鋼材。

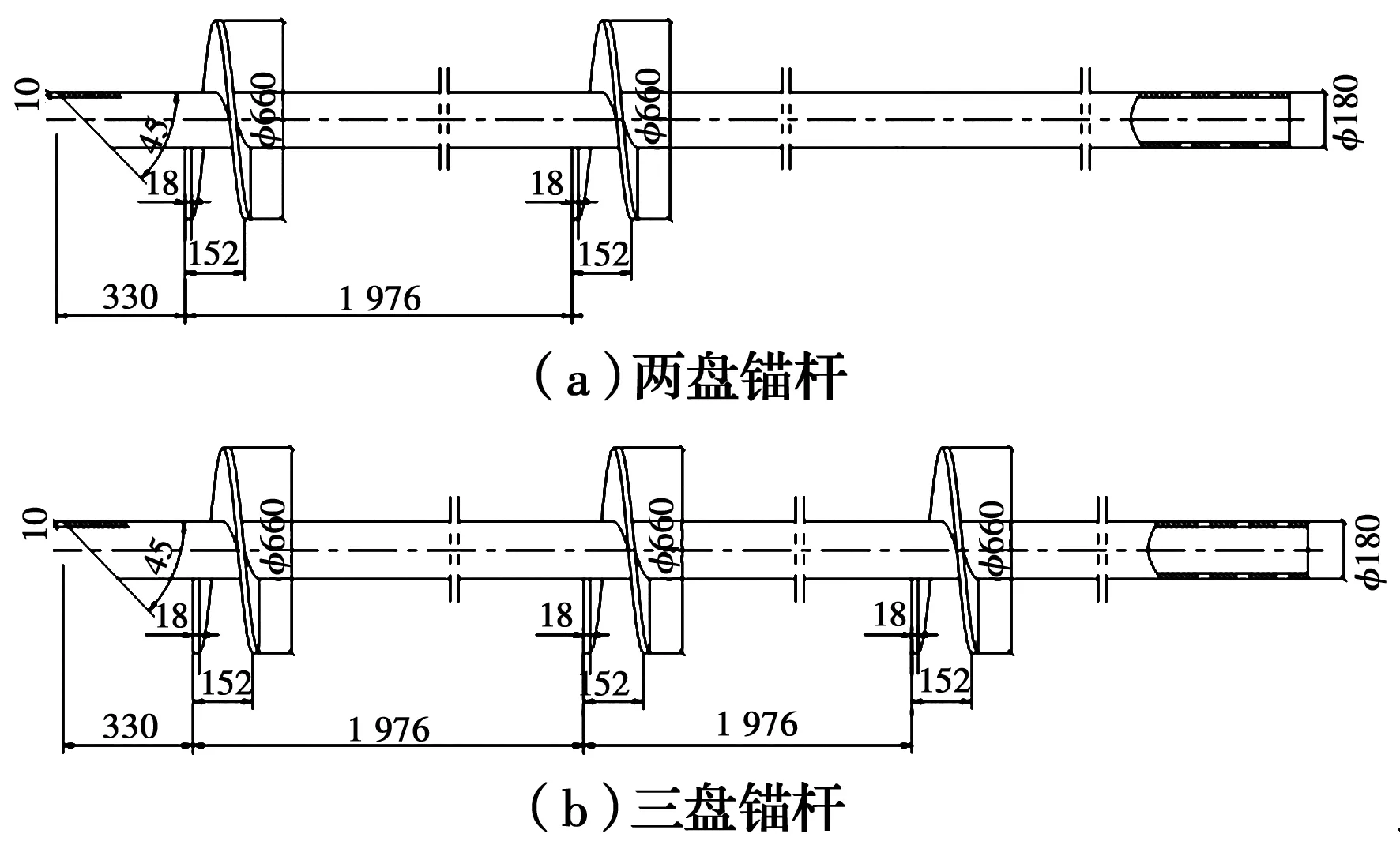
圖3 螺旋錨加工尺寸(單位：mm)

2.2 試驗結果

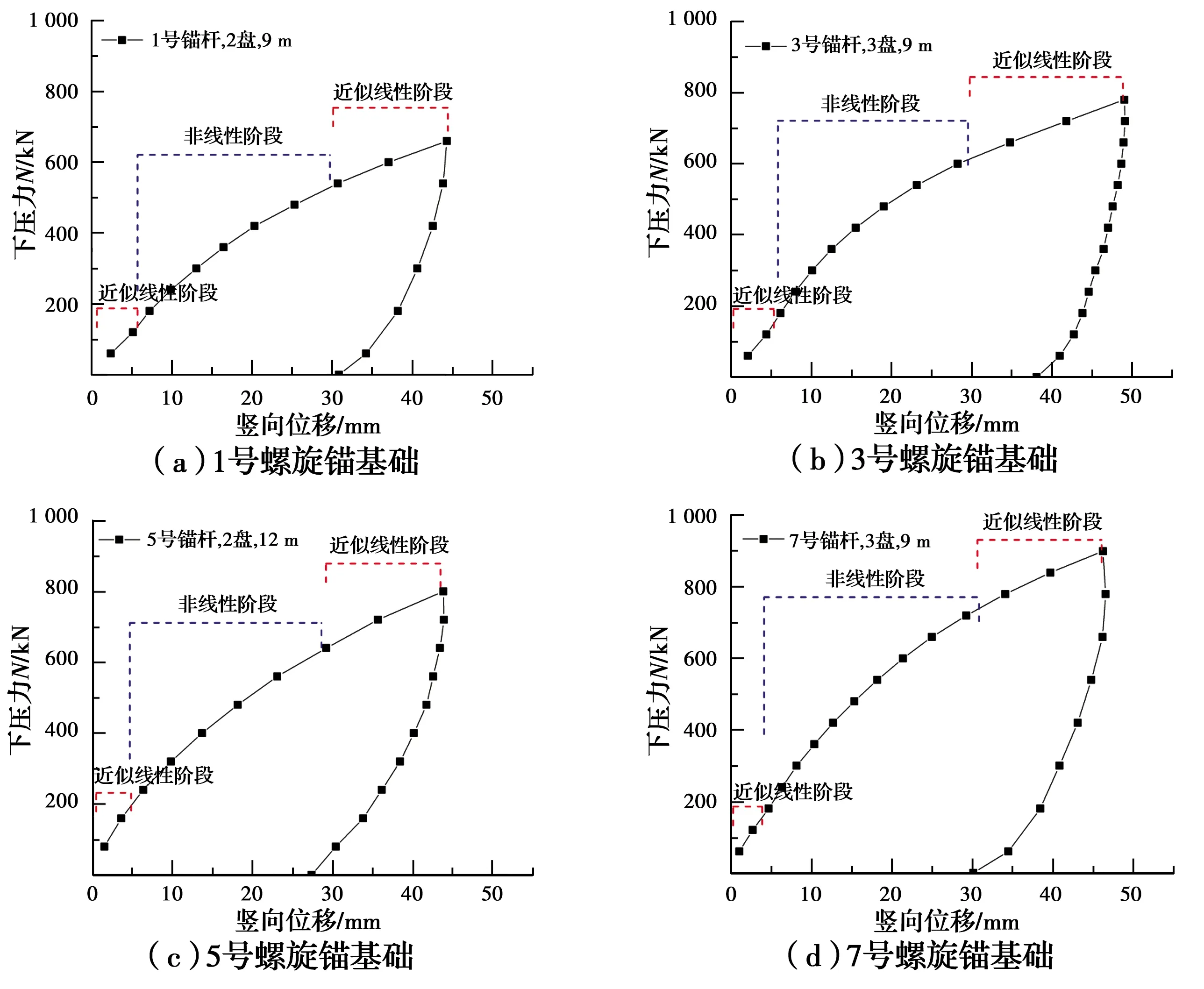
圖4 靜載試驗結果

7號與3號均為3錨盤螺旋錨基礎，埋深均為9 m。根據試驗結果，7號承載力為3號承載力的1.15倍，而5號承載力位于兩者之間，三者均大于1號螺旋錨。可見，單錨抗壓承載力隨錨盤數量的增加而增大，隨埋深的增加而增大，3盤9 m的單螺旋錨基礎抗壓承載力與2盤12 m的單螺旋錨基礎承載力相當。

2.3 極限承載力確定方法對比

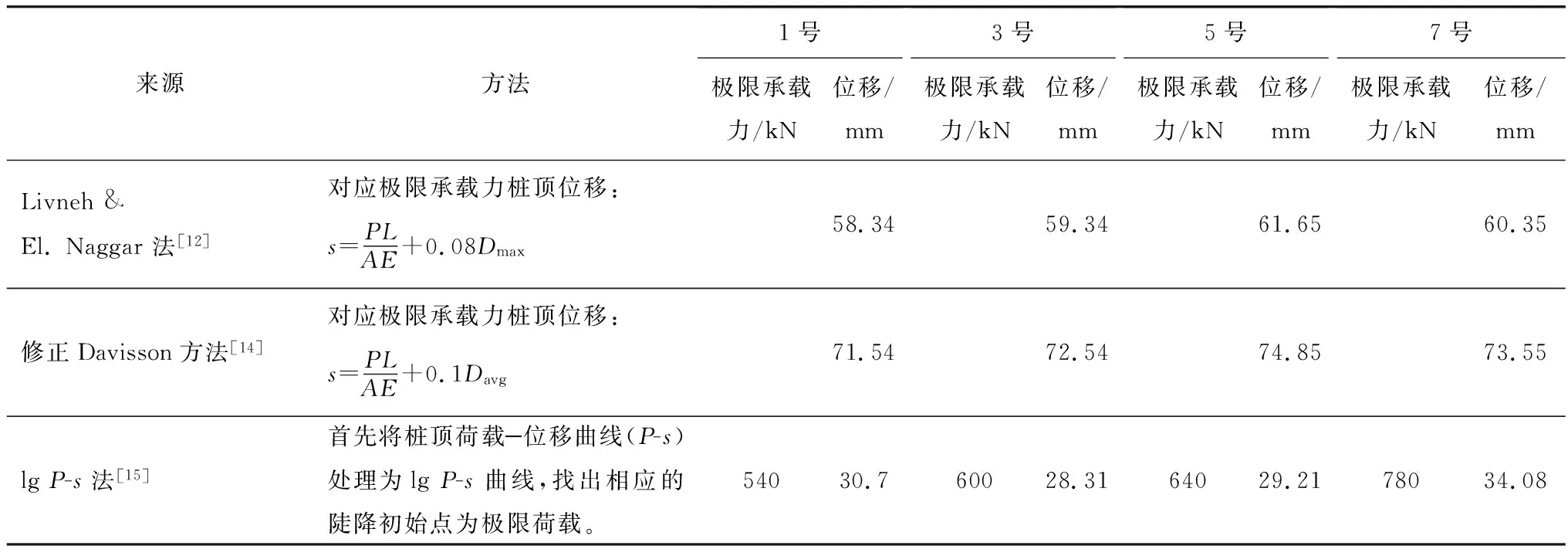
表2 不同方法確定螺旋錨承載力

2.4 極限承載力確定方法討論與建議

通過上述針對極限承載力確定方法的對比發現，軸向壓力作用下，由于錨片直徑較大，基礎錨桿側摩阻力完全發揮時對應的位移與錨片直徑的比值較小。如果仍然按照常規螺旋錨基礎極限承載力判別條件，通過錨盤直徑一定比例的位移對應的荷載作為承載力，則此時承載力會偏大甚至無法得到。可見，前兩種方法不適用于大葉片螺旋錨基礎。第3種方法通過對處理后的曲線做切線，找到陡降段的起始點，如圖5所示。該方法能夠較合理地找到螺旋錨基礎對應的極限狀態，說明該方法適用于黏土地層中的大錨片螺旋錨基礎。

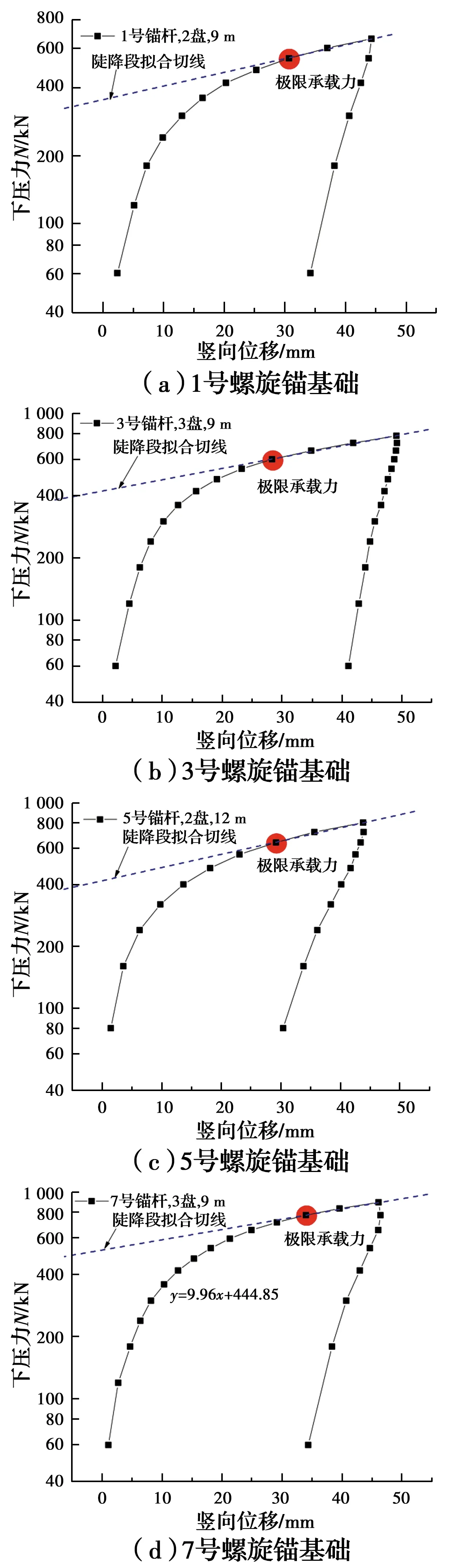
圖5 lg P-s法確定螺旋錨桿承載力

3 靜載試驗數值模擬與結果分析

3.1 計算模型

利用有限元軟件ABAQUS對螺旋錨進行豎向加載數值模擬，為了消除邊界條件對計算結果的影響，計算模型中，土體水平范圍取為錨盤直徑的10倍，土體豎向范圍取為螺旋錨埋入深度的2倍，如圖6所示。根據實際試驗條件，對土體底部約束3個方向的平移自由度，土體側面約束水平兩個方向的平移自由度。螺旋錨基礎與土體建立接觸，接觸面的本構關系即為相互作用的力學模型，其中包括兩個部分，分別是：接觸面的切向作用和法向作用[16]。在模擬接觸作用中法向使用硬接觸模塊“Hard Contact”，這種接觸對于兩個物體來說只有在壓緊的狀態下才會傳遞法向壓力，并且保證限制住了穿透現象的發生；切向作用使用的是“Penalty”罰函數，允許發生彈性滑移變形，并且設定摩擦系數為0.14。

圖6 有限元模型

在對螺旋錨基礎數值分析中，通常為了提高計算收斂效果，將螺旋盤簡化成平盤進行計算[17-20]。為了充分驗證錨盤形式對基礎承載力的影響，在同樣的邊界條件和荷載作用下，分別對錨盤為螺旋狀和平盤狀的基礎進行數值分析，對比壓力荷載下計算結果的差異性，如圖7所示。其中，在對螺旋錨盤與錨桿連接部分劃分網格時，先對錨桿壁沿螺旋線進行切割，以繪制出高質量的網格。

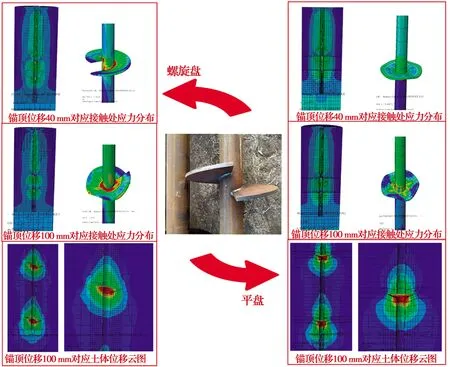
圖7 不同錨盤形式數值分析結果對比

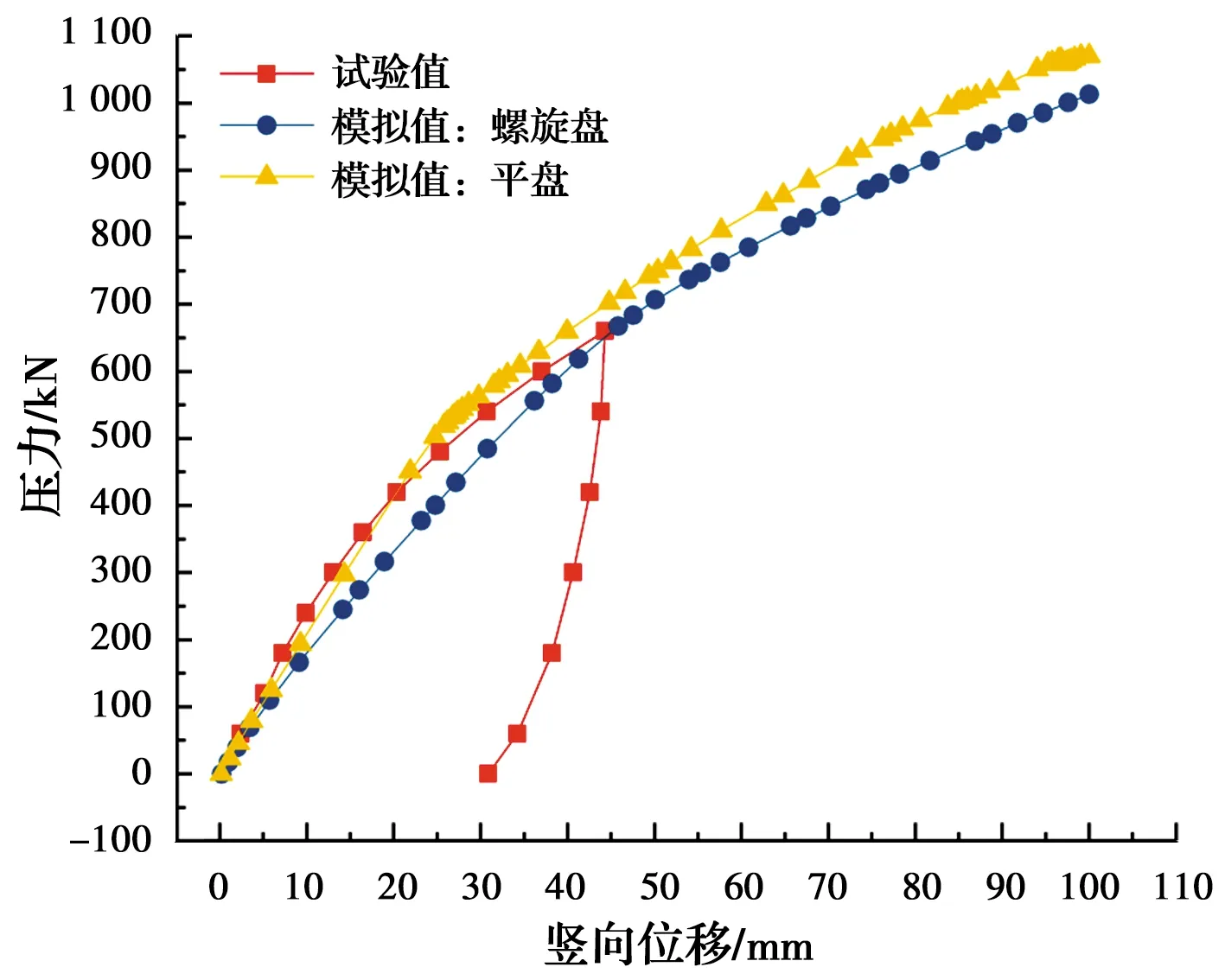
圖8 1號螺旋錨基礎下壓荷載位移曲線

3.2 參數選取

表3 金屬本構的相關參數

3.3 有限元模型驗證

為了能夠較準確地模擬螺旋錨基礎在土中的受力情況，數值分析的第一步是進行地應力平衡。由于初始狀態的土單元在重力作用下會發生較大的豎向壓縮變形，在土與錨桿接觸面上，由于相對滑動過大而造成計算難以收斂。為了提高計算效率，在地應力平衡計算中不激活接觸面，以便較快且準確地得到初始地應力場。

為了能夠較真實地模擬錨桿周邊土體對其摩阻力，需要考慮螺旋錨鉆入土的過程中對周邊土體的擠壓效應。地應力平衡分析完成之后，激活螺旋錨與土之間的接觸面，但在此狀態下錨桿與周圍土的相互擠壓力很小，此時，螺旋錨在豎向荷載作用下，其錨頂壓力主要由錨盤承擔，而錨桿上的側摩阻力近似為0，顯然不符合基礎的實際受力狀態。為了更加真實地模擬壓力作用下的螺旋錨在土中受力情況，需要在接觸面上設置初始擠壓力。初始擠壓力的施加通過螺旋錨與土接觸面之間的過盈分析來實現，過盈量取錨軸的半徑。

圖9 下壓分析初始地應力場

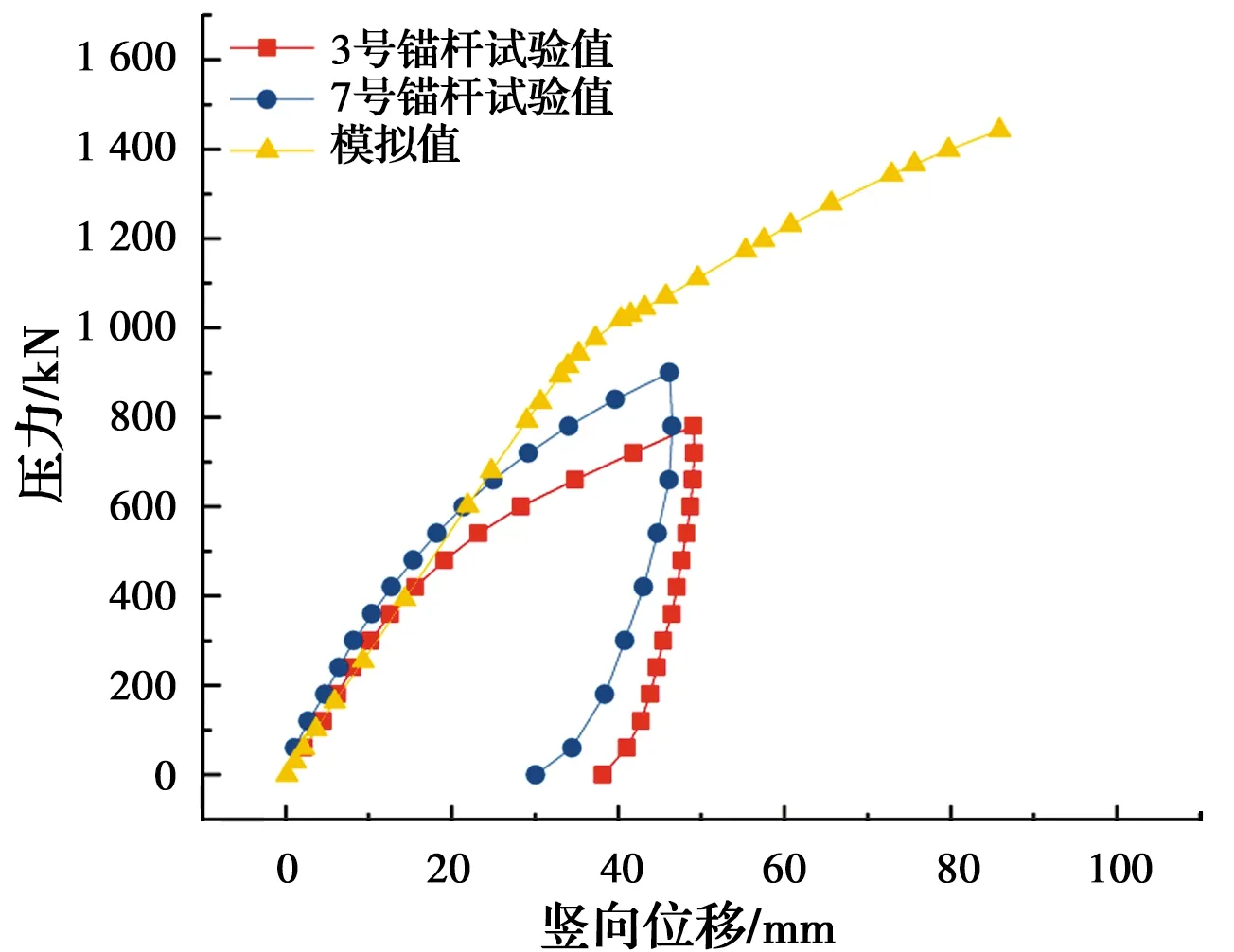
圖10 3號、7號螺旋錨基礎數值模擬與現場實測對比

圖11 5號螺旋錨基礎數值模擬與現場實測對比

4 豎向荷載下螺旋錨受力性能

數值分析結果與試驗結果的對比驗證了有限元模型的可靠性。采用數值分析方法分析不同等級荷載下螺旋錨軸力、側摩阻力分布和荷載分擔規律。

4.1 內力變化規律

基于有限元計算結果，提取錨桿沿縱向的軸力、剪力和彎矩，如圖12～圖14所示。通過對比分析可知，螺旋錨在軸向壓力作用下，錨桿上的剪力和彎矩非常小，可忽略不計。

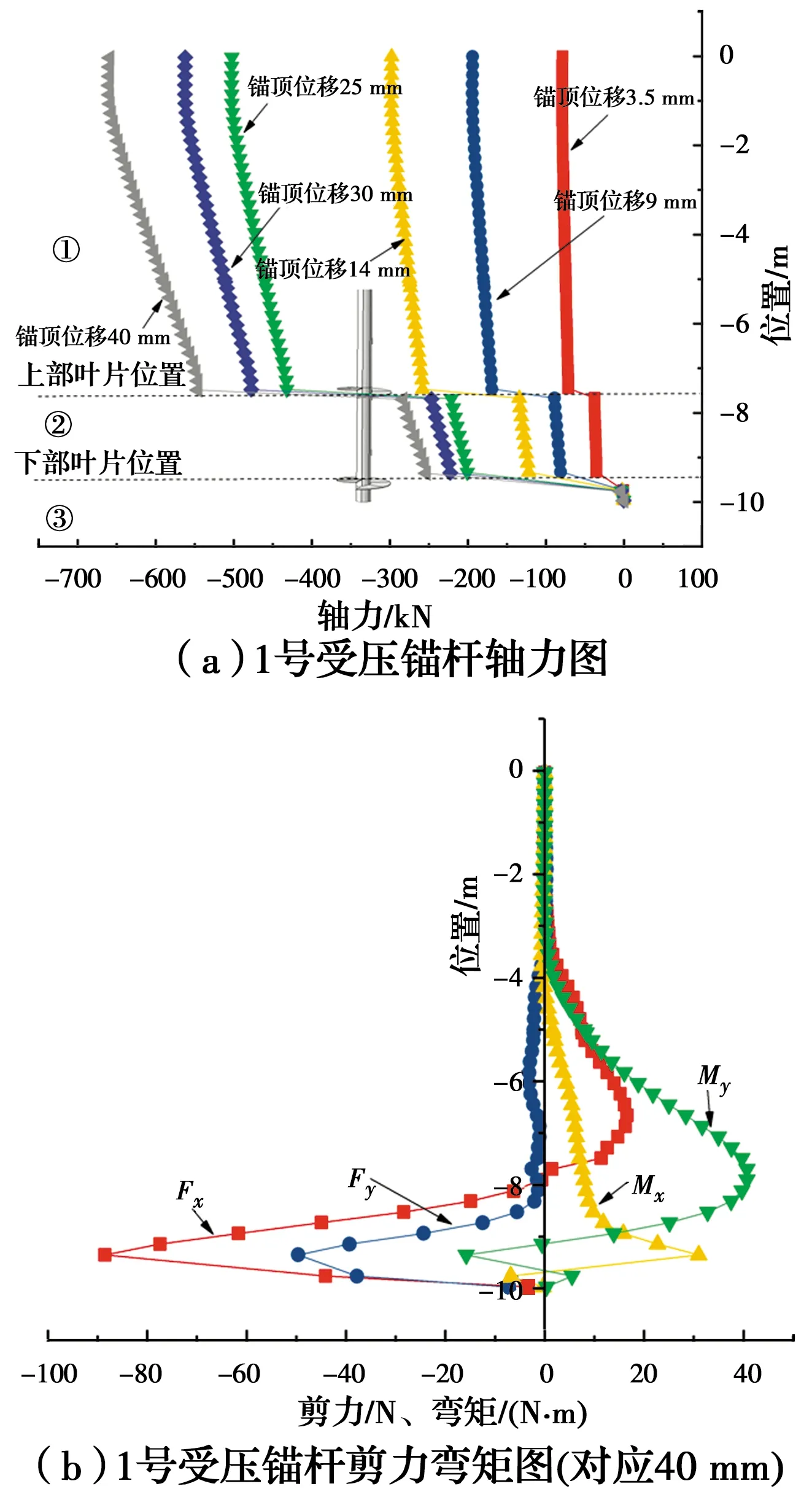
圖12 1號螺旋錨基礎的錨桿內力圖

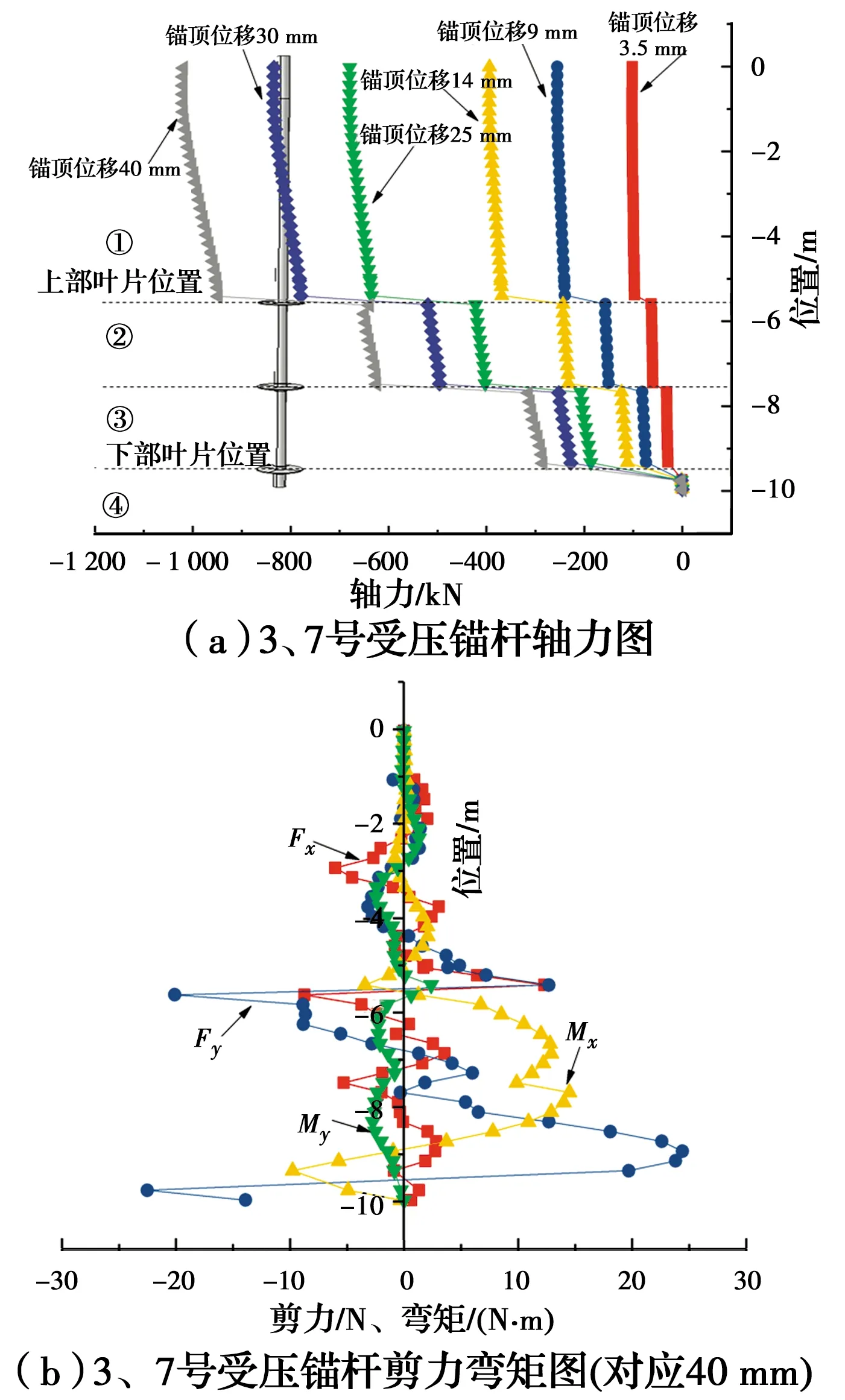
圖13 3、7號螺旋錨基礎的錨桿內力圖

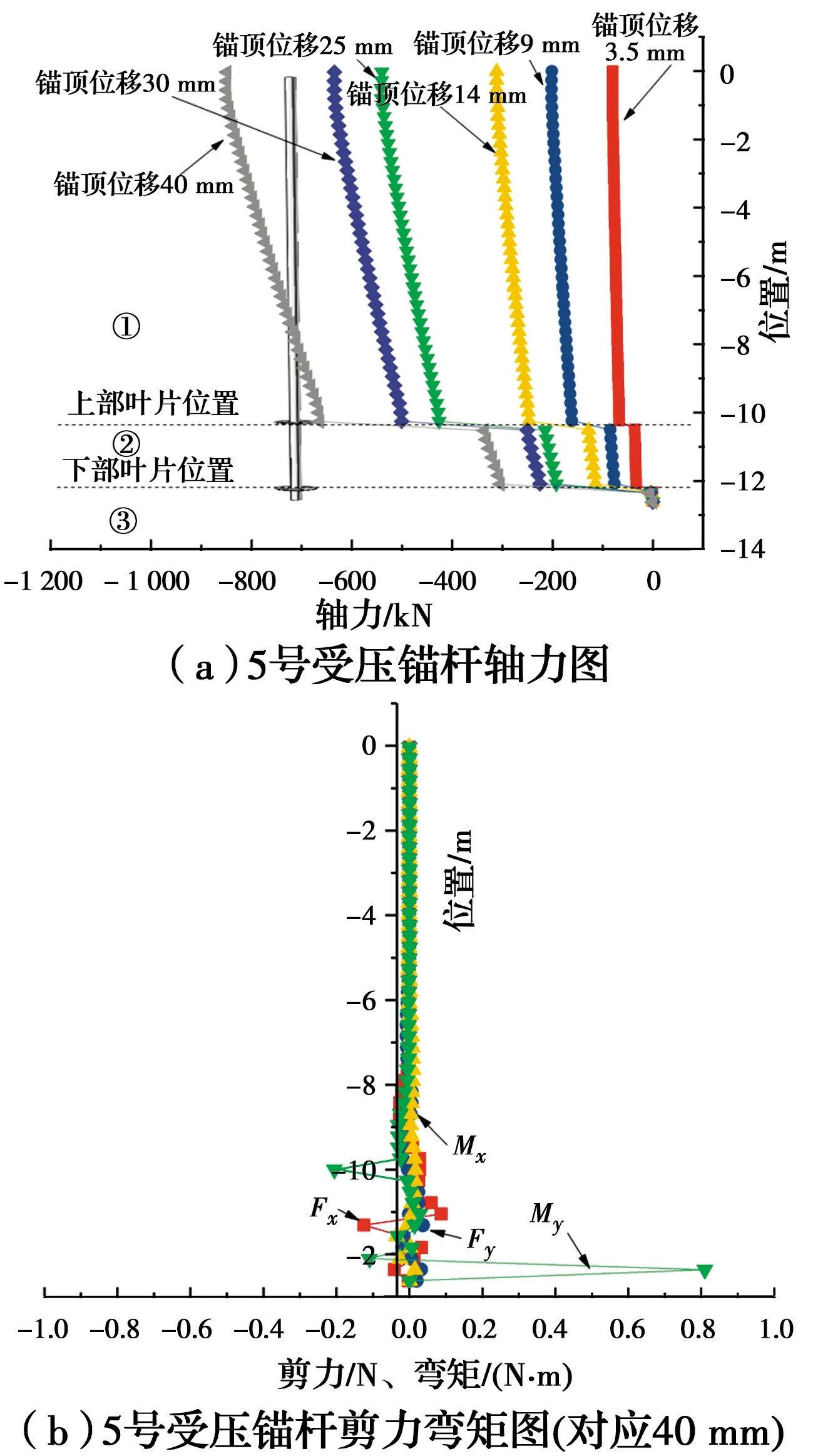
圖14 5號螺旋錨基礎的錨桿內力圖

對于錨桿軸力，隨著錨頂位移的增加，軸力圖中的①區段斜率逐漸增大，說明隨著施加荷載增加，錨桿側摩阻力逐漸增大。同時，在不同錨頂位移對應下的螺旋錨基礎的錨桿軸力在錨片附近均發生突變，說明錨片在螺旋錨基礎的整個受力過程中均參與分擔，即使初始加載時荷載和位移都很小。

如圖12(a)中的區段②、13(a)中的區段②和③以及14(a)中的區段②所示，隨著錨頂位移的增加該區段內的軸力圖斜率也逐漸增加，說明錨片之間的錨桿側阻對抵抗外部壓力是有貢獻的，并且與區段①保持著同樣的規律，但是該區段軸力圖的斜率要小于區段①。

如圖12(a)中的區段③、13(a)中的區段④以及14(a)中的區段③所示，該部分的軸力在0附近，說明該區段以上的錨盤端阻力和錨桿側摩阻基本上已經全都抵消掉了外部壓力的作用，同時也說明了錨桿底部端阻在整個受力過程中幾乎不發揮作用。

4.2 側向摩阻力變化規律

通過對錨桿內力的分析可知，錨桿側摩阻在螺旋錨基礎的整個受力過程中發揮著重要作用，如圖15～圖17所示，隨著錨頂位移的增加，錨桿側摩阻逐漸增大。這是由于螺旋錨在軸向壓力作用下會發生向下的整體位移，土體與螺旋錨的接觸面存在摩擦力，螺旋錨周邊的土體會隨著基礎一同發生向下的壓縮變形。隨著壓力的增大，土體的豎向壓縮也隨之增大，土體越來越密實并且對螺旋錨基礎的擠壓力也越來越大，錨桿的側摩阻也隨之增大。

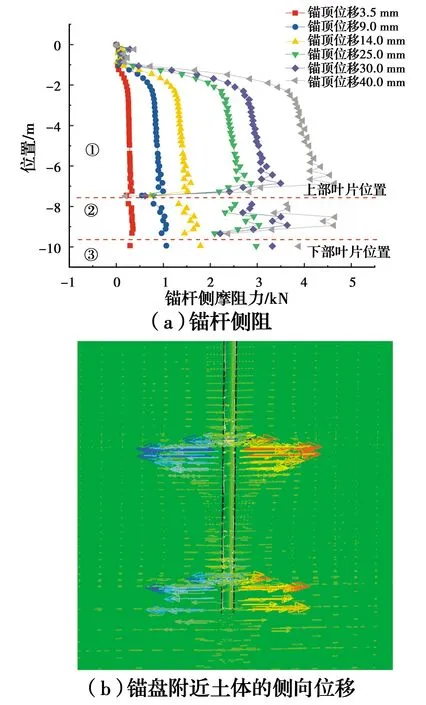
圖15 1號螺旋錨基礎的錨桿側向摩阻力

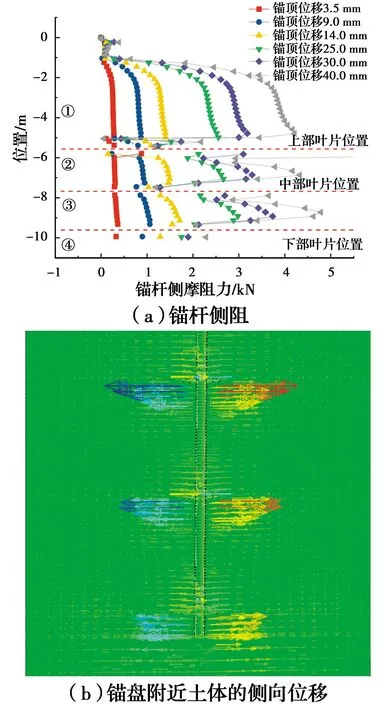
圖16 3、7號螺旋錨基礎的錨桿側向摩阻力

如圖15～圖17所示，螺旋錨基礎葉片附近的錨桿側阻會突變減小。對葉片附件的土體變形分析可知，螺旋錨葉片在壓力作用下會發生下凸變形，變形后的葉片會對周圍土體產生側向外推，從而使葉片附近的土體與錨桿脫離，如圖15～圖17中的(b)所示，脫離部分的摩阻力為0，未脫離部分仍然保持著原有的摩阻力，但葉片之間的錨桿側摩阻整體來說還是削弱了。

4.3 荷載分擔規律

通過分析可知，螺旋錨基礎在軸向壓力的作用下，其抵抗力主要由錨桿側摩阻和錨片端阻來提供，錨桿端阻基本上不發揮作用，螺旋錨基礎的荷載分擔如圖18所示。對于小葉片砂土中的螺旋錨基礎，在豎向受荷過程中，首先是錨桿側摩阻發揮作用，其次各個葉片由上至下相繼發揮端承作用，最后下部葉片和錨桿底部發揮端承作用繼續承擔上部荷載[10]。但是，對于大錨片黏土中的螺旋錨卻顯示出不一樣的分擔規律，見表4～表6，在荷載施加過程中，不同錨片之間分擔的荷載基本相等，且錨片端阻分擔的荷載占螺旋錨基礎上總荷載的75%～90%，可見大葉片螺旋錨基礎可以視為端承摩擦型樁。

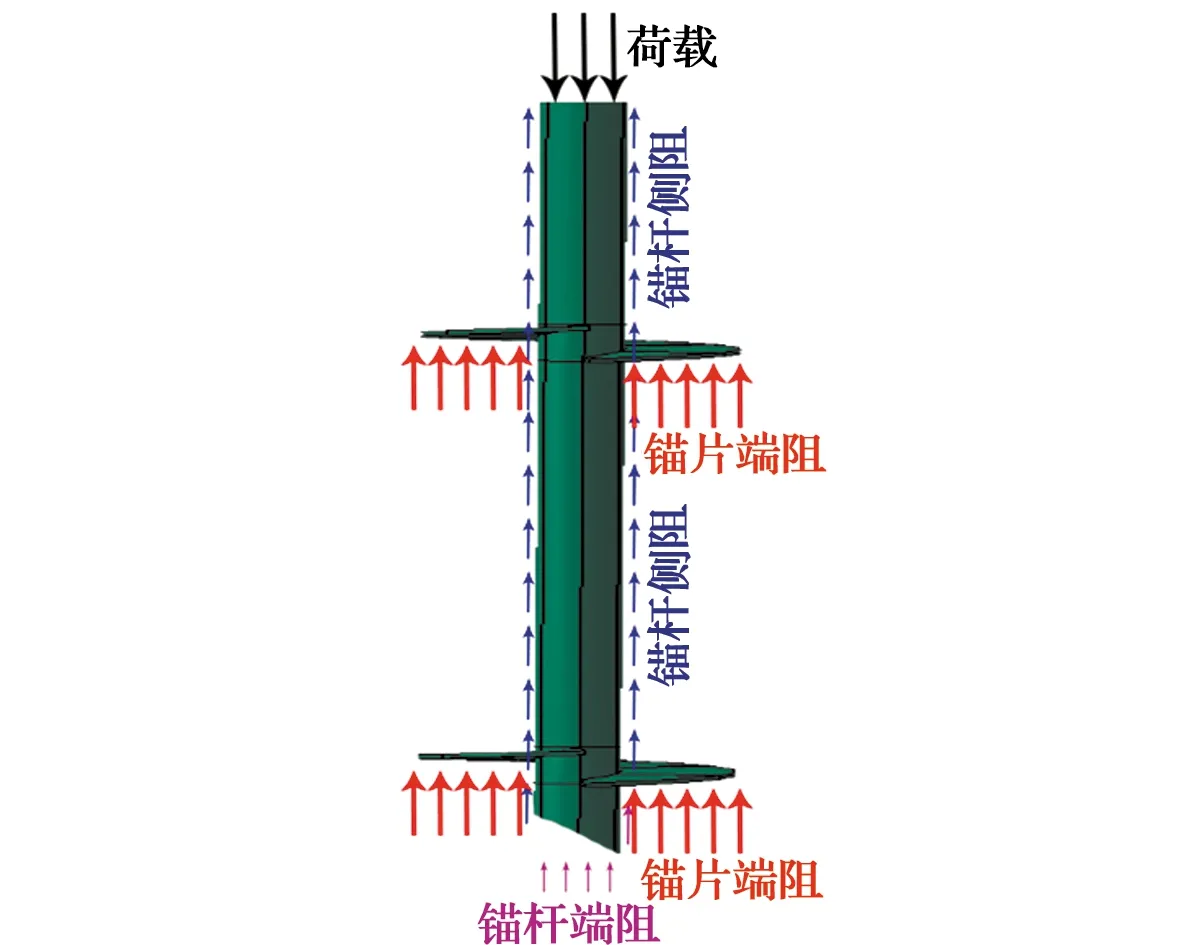
圖18 螺旋錨基礎的荷載分擔示意圖

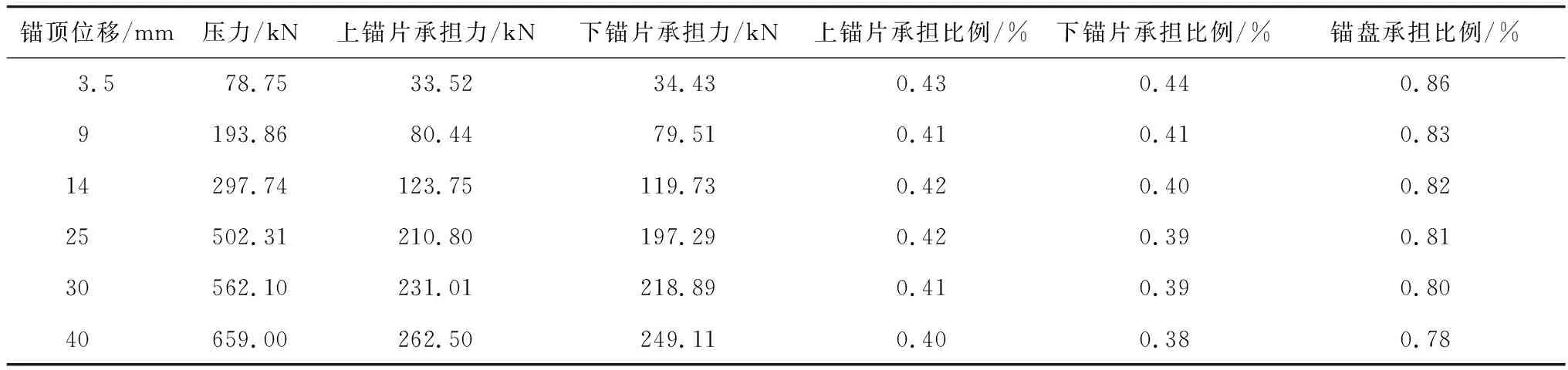
表4 1號螺旋錨基礎荷載分擔比例

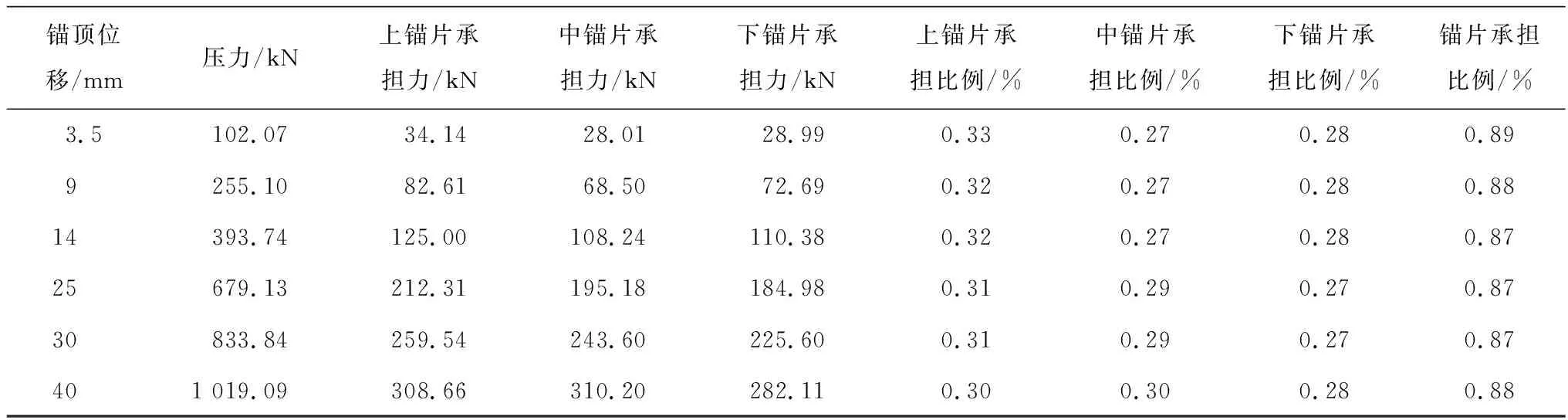
表5 3、7號螺旋錨基礎荷載分擔比例

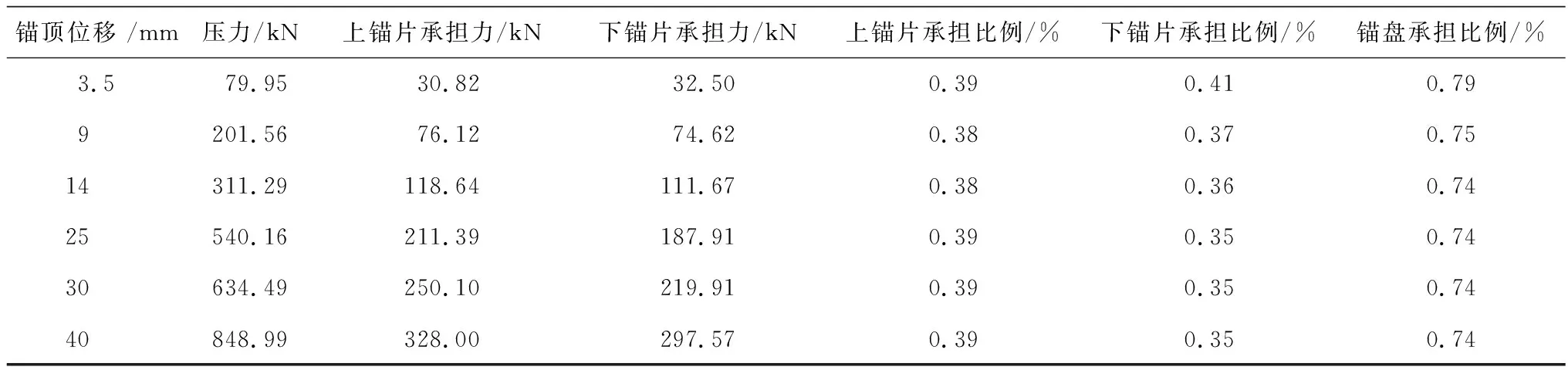
表6 5號受壓錨荷載分擔比例

對比表4和表6可知，對于大葉片螺旋錨基礎，當葉片數量不變時，隨著埋深的增加錨桿側摩阻所占的比重增加。對比表4和表5可知，螺旋錨基礎埋深不變時，隨著錨片數量的增加，錨桿側摩阻所占的比重降低。

隨著施加荷載的增大(表4)，螺旋錨基礎最上部錨片和最下部錨片承擔荷載的比例都有所降低。其主要原因是，錨片彎曲變形降低了與土體的有效接觸面，從而減少了錨片的承擔荷載比例，且上部錨片承擔的荷載比例基本上均略大于下部錨片。

隨著施加荷載的增大(表5)，螺旋錨基礎最上部錨片承擔荷載的比例隨之降低，中部錨片承擔的比例同步增加，下部錨片承擔荷載比例基本不變。說明隨著荷載的增大，上部錨片的變形要大于中部錨片，隨著變形的不斷加大，上部錨片承擔的部分荷載傳遞到中部錨片。在螺旋錨受力過程中，上部錨片承受荷載的比例最大，中部錨片隨著施加荷載的增加，承擔荷載的比例逐漸增大，并且在錨頂位移大于25 mm時，其承擔比例大于下部錨片。

隨著施加荷載的增大(表6)，螺旋錨基礎最上部錨片承擔荷載的比例基本不變，而下部錨片承擔的荷載比例逐漸減小。

綜上所述，大葉片螺旋錨基礎隨著施加荷載的增加，在不同錨片個數以及不同埋深的條件下，各個錨片端阻和錨桿側摩阻分擔荷載的比例發生不同規律的變化，最大變化幅值約為8%。錨片分擔荷載的比例占據螺旋錨基礎受荷過程的總荷載75%以上，各個錨片分擔荷載比例最大差異約為6%。

5 結論

基于粉質黏土場地的大錨片螺旋錨基礎的現場靜載試驗和數值模擬，分析基礎在豎向壓力作用下極限承載力的確定方法和荷載傳遞特性，得到以下結論：

1)對于大錨片螺旋錨基礎，采用lgP-s方法確定極限承載力較Livneh & EL.Naggar法與修正的Davisson法更合理。

2)螺旋錨在軸向壓力作用下，錨桿上的剪力和彎矩與軸力相比非常小，可忽略不計。隨著施加荷載增加，錨桿側摩阻力逐漸增大。在不同錨頂位移對應下的螺旋錨基礎的錨桿軸力在錨片處均發生突變，錨片在螺旋錨基礎的整個受力過程中均參與承擔外部壓力。

3)大錨片螺旋錨基礎隨著施加荷載的增大，在不同錨片個數以及不同埋深的條件下，各個錨片端阻和錨桿側摩阻分擔荷載的比例發生不同規律的變化，最大變化幅值約為8%。錨片分擔的荷載占據螺旋錨基礎受荷過程的主要部分(75%以上)，各個錨片分擔荷載比例最大差異約為6%。建議在實際工程中盡可能將葉片布置在承載力較高的土層中，并且各個錨片可近似認為對基礎的承載力貢獻相同。

未來的研究工作中需進一步對大錨片螺旋錨基礎在不同的錨片數量和間距下進行參數分析，以揭示大錨片螺旋錨基礎在壓力荷載作用下的內力傳遞機理和不同錨片之間的分配機制，為該類型基礎承載力計算理論研究提供支撐。