基于新型流形法的三維應力強度因子求解
祁勇峰,蘇海東,龔亞琦
(長江科學院 材料與結構研究所;水利部水工程安全和病害防治工程技術研究中心,武漢 430010)
應力強度因子準則[1]是目前最常用的結構裂縫擴展準則之一,基于線彈性斷裂力學的應力強度因子(Stress Intensity Factor,簡稱SIF)是用來表征裂紋尖端附近應力場和應變場強度,是控制裂紋尖端應力場和應變場強度的關鍵參數,在裂紋擴展分析中有著極其重要的地位。由于應力強度因子取決于外力的大小和分布、結構的幾何條件以及裂縫的形狀和位置,實際上只有少數問題存在解析解,對于復雜幾何形狀和加載條件的問題,只能通過數值方法來計算。目前裂縫擴展分析的主流數值計算方法有有限元法、擴展有限元法、數值流形法等。
有限元法[2-4]是目前分析裂縫等不連續問題的主要方法,為體現裂紋尖端(下簡稱裂尖)周圍的應力集中和奇異性,往往需要在裂尖附近的復雜應力區布置高密度的單元網格,導致單元數目非常龐大;另外,在模擬裂縫擴展過程時,需不斷重構網格,因此,有限元法對網格的要求和依賴性極大地影響了計算效率。擴展有限元法[5-7]通過在單元插值函數中引入能夠反映裂縫面特性的不連續階躍函數及反映裂尖局部特性的裂尖漸進位移場函數,裂縫可以穿過單元內部,裂縫擴展以后無需重新劃分單元網格,采用同一網格就可以分析任意位置的裂縫問題,克服了常規有限元進行裂縫擴展分析的缺點,極大地簡化了前處理工作。數值流形方法[8-11]引入不連續覆蓋模擬裂縫,裂縫可以在網格內部穿過,巧妙地解決了常規有限元法裂縫面必須與單元邊一致、裂縫擴展后需要重新劃分網格的問題。相對于擴展有限元法設立不連續階躍函數的方式而言,這種方式效果更好,在裂縫非常靠近單元邊界時不會產生后者容易出現的數值誤差。但無論是常規有限元法在裂尖布置細密網格的方式,還是擴展有限元法引入裂尖漸近位移場的方式,其主要目的都是為了提高裂尖附近的求解精度,從而提高應力強度因子的計算精度,這些方法都有改進的余地。即使是目前認為最適合于裂縫擴展分析的擴展有限元法,由于其只是使用了裂尖漸近位移場的部分特征函數,嚴格地說,還不能構成對裂尖位移場的最佳逼近。文獻[12]提出的新型數值流形方法,實現了裂紋尖端的解析解與其周邊數值解聯合應用以求解應力強度因子,能夠采用裂尖真實位移場的最佳逼近,并直接得到應力強度因子,計算精度高,但僅限于平面問題的Ⅰ型和Ⅱ型裂紋。
在上述研究的基礎上,沿用解析解與數值解聯合應用的思路,在裂紋尖端直接引入Williams解析解作為數學覆蓋,應用裂紋尖端的解析解與周邊數值解的三維流形覆蓋聯系技術,可直接得出裂紋尖端的三維應力強度因子,精度高且計算收斂快。
1 裂紋尖端位移場的Williams級數解
如圖1所示的裂紋尖端區域,Williams位移級數解
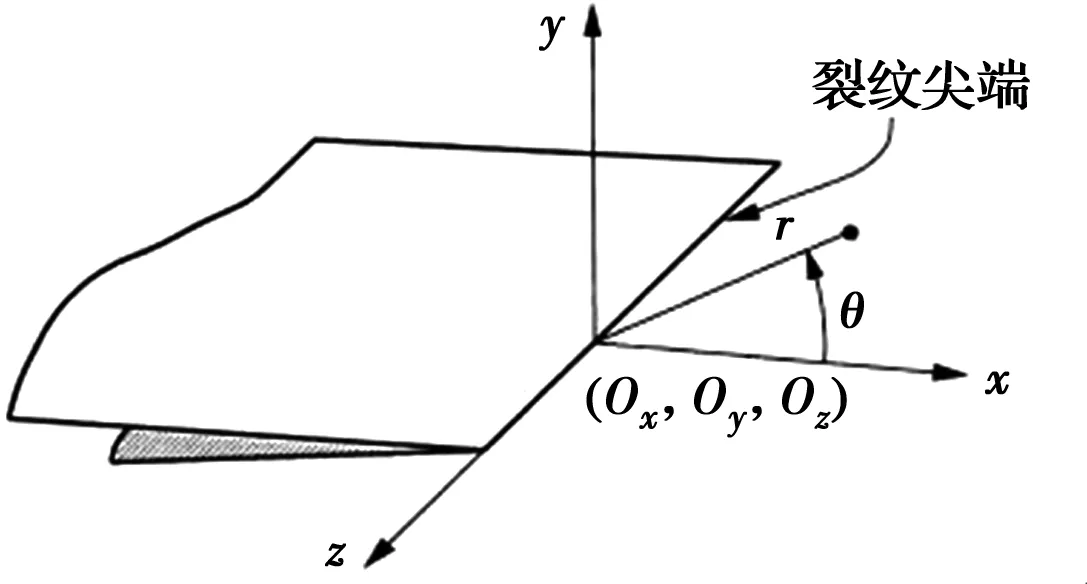
圖1 裂紋尖端坐標系
(1)
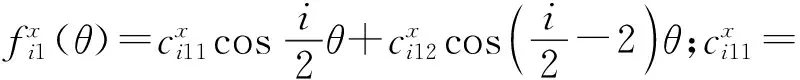
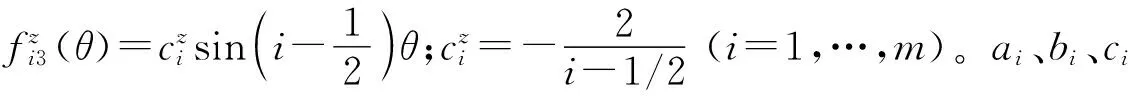
(2)
2 裂紋尖端位移場的解析解覆蓋
在六面體網格內,將式(1)寫成矩陣形式。
對于i=0:
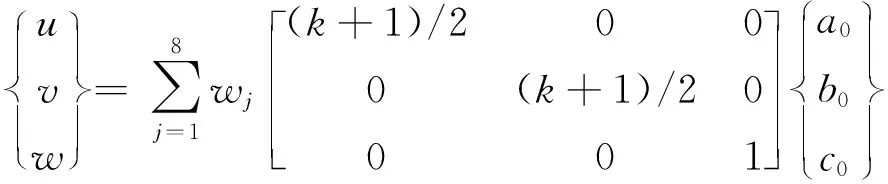
(3)
對于i≥1:
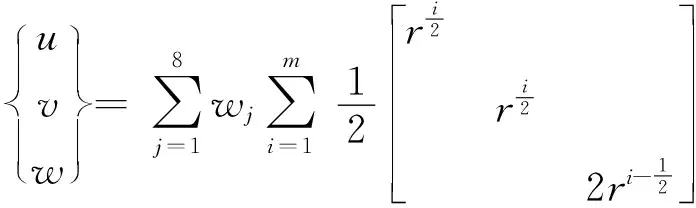
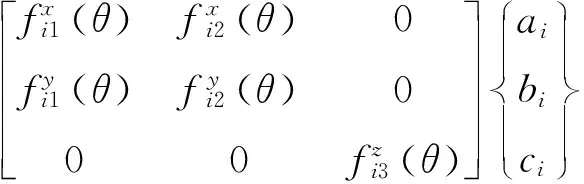
(4)
將二維數值覆蓋強制約束方法[13]推至三維,形成獨立的三維解析覆蓋,權函數wj均為結點1的權函數w1。其中,m為覆蓋函數項數,下同。
對于第i項(i≥1),其應變子矩陣為
(5)
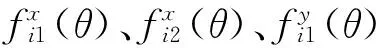
(6)
將各項偏導數展開
(7)
式中:
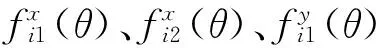
另外,
剛度子矩陣
(8)
式中:D為彈性矩陣;V為流形元體積。
3 裂紋周邊網格的解析解與數值解覆蓋
在裂紋周邊的各網格內,位移統一表示為式(9),其中i≥1。
(9)
式中:dnkl、enkl、fnkl為待求的多項式系數;n、k、l為多項式階次(p為多項式的最高階次);wj1、wj2為相應于各結點的權函數;J和L的個數根據網格而定,但保持J+L=8。顯然,取L=0則退化到解析解覆蓋式(4)。
如圖2所示(圖中窄條為部分重疊區域,長方體區域為獨立覆蓋,陰影為裂紋),采用強制約束的方法,將網格結點28、40、39、33、34、45、46約束到結點27,即令
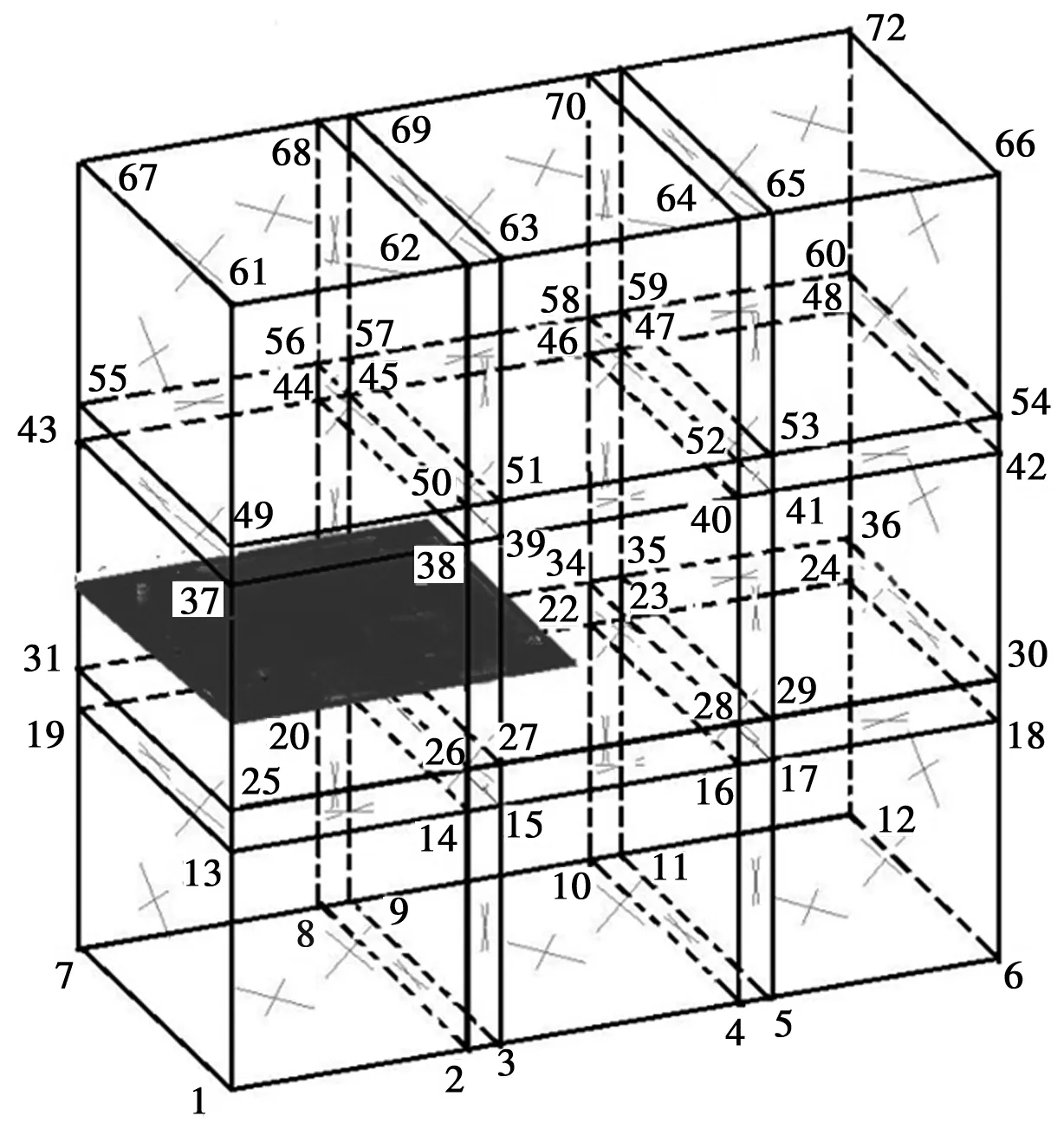
圖2 六面體數學網格中的解析解覆蓋和數值解覆蓋
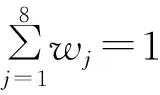
對于周邊的其他網格,比如:網格1-2-14-13-7-8-20-19中的結點均為數值解的獨立覆蓋;解析覆蓋的相鄰網格39-40-52-51-45-46-58-57中的結點39、40、45、46為解析結點,其他4個結點為數值結點;而裂紋自由端所在網格25-26-38-37-31-32-44-43在豎直方向采用了兩個獨立覆蓋,實現裂紋兩邊的獨立運動。
對于解析覆蓋結點j處的第i項,其應變矩陣為
(10)

(11)
令f(x,y,z)=xn-k-lylzk,則式(11)可寫為
(12)
解析覆蓋與數值覆蓋相關的剛度子矩陣為
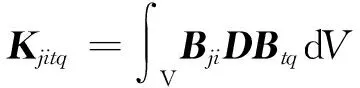
(13)
由式(10)和式(12)可見,剛度矩陣積分中具有非多項式的函數,基于多形式函數的單純形積分公式無法應用,必須采用數值積分。因此,采用四面體區域的Hammer積分[14],將流形元邊界上的三角片與其形心相連形成四面體,然后再進行積分計算。
4 算例分析
以含邊界裂紋的無限長柱體為例,考慮兩種不同類型荷載。
4.1 兩端受均布拉力
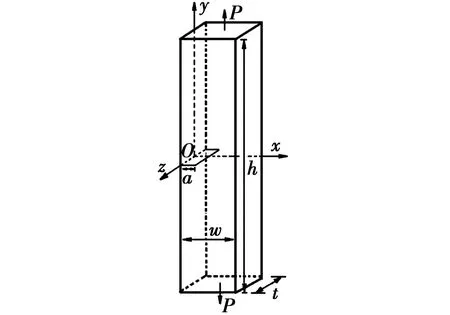
圖3 兩端受均布拉力的無限長柱體內的邊界裂縫
整體的流形元網格如圖4所示,共劃分6個獨立覆蓋和9個部分重疊覆蓋(窄條區域),每個獨立覆蓋的大小基本相同。裂紋所在的獨立覆蓋區域大小為0.65 m×0.2 m×1 m(長×寬×厚),柱體底面施加法向約束。
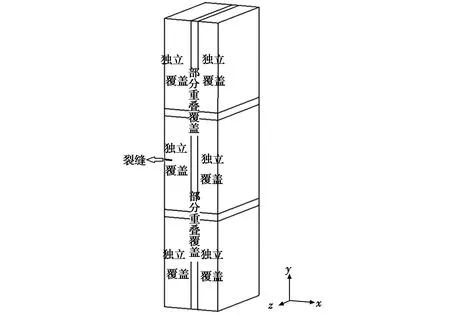
圖4 部分重疊覆蓋的流形元網格
應力強度因子的計算結果見表1,考慮了裂紋尖端所在的獨立覆蓋取Williams級數的不同項數,獨立覆蓋周邊的數值解覆蓋可取多項式的不同階數。
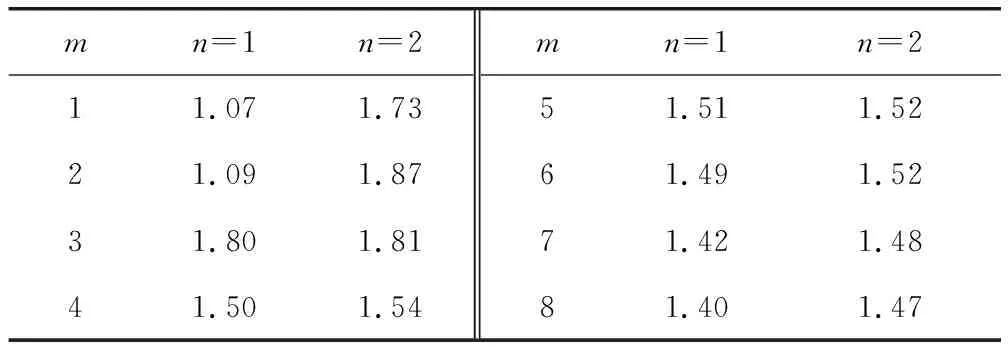
表1 應力強度因子
隨著覆蓋函數階數的增加,三維應力強度因子計算值基本接近理論值。Williams級數的階數以及周邊數值覆蓋階數對計算值有較大影響。
1)Williams級數的階數(m)影響最大。當m≤3,則KI與理論值相差較大;當m≥4時,KI接近理論值。
2)周邊數值覆蓋階數升高有利于提高解的精度。當周邊數值解取1階時,KI的計算值普遍小于取2階的情況,當m≥4時,KI與理論值接近,但仍有差距,僅當m取為7時才達到1.42,與理論值1.45最為接近。而當周邊數值覆蓋取2階,m≥7時,計算值與理論值基本一致。
前期平面問題研究表明,在大的覆蓋中單純依靠提高覆蓋函數階次的方法往往會帶來計算結果的振蕩跳躍。反之,如果采用較小的覆蓋而用相對簡單的低階多項式,則可以更好地逼近實際復雜的分布情況。表2的計算結果也說明,三維問題中,基于大覆蓋,僅僅采用提高級數解及相鄰覆蓋函數的階數的做法來提高計算精度,計算也表現出一定的不穩定性,要取得滿意的計算精度,裂紋尖端及其周邊的覆蓋函數的階數不小于7階。
考慮到裂紋所在的獨立覆蓋區域較大,因此,將裂紋所在的獨立覆蓋進行局部加密,將裂紋尖端覆蓋分別加密1倍及2倍,采用局部覆蓋加密技術[16],重新計算應力強度因子,如表2所示。
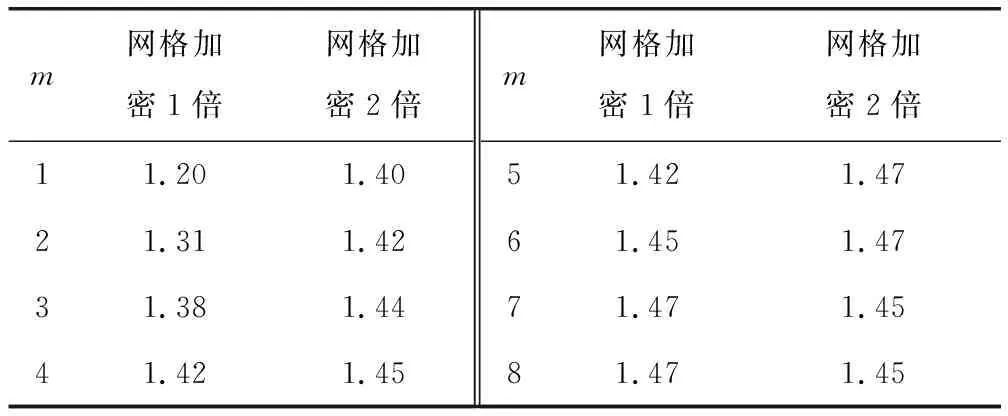
表2 應力強度因子(n=2)
表2結果表明,當裂紋尖端獨立覆蓋加密1倍后、Williams級數的階數≥4或當裂紋尖端獨立覆蓋加密2倍后,Williams級數的階數≥3時,KI與理論解十分接近,且隨著Williams級數階數的提高,計算結果趨于穩定。
4.2 兩端受剪切荷載作用
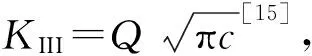

圖5 兩端受剪力的無限長柱體內的邊界裂縫
流形元網格如圖6所示,共劃分18個獨立覆蓋(方塊區域)和25個部分重疊覆蓋(窄條區域),每個獨立覆蓋的大小基本相同。裂紋所在的獨立覆蓋區域大小為0.2 m×0.2 m×1 m(長×寬×厚),柱體底面施加法向約束。應力強度因子的計算結果見表3。
圖6 部分重疊覆蓋的流形元網格
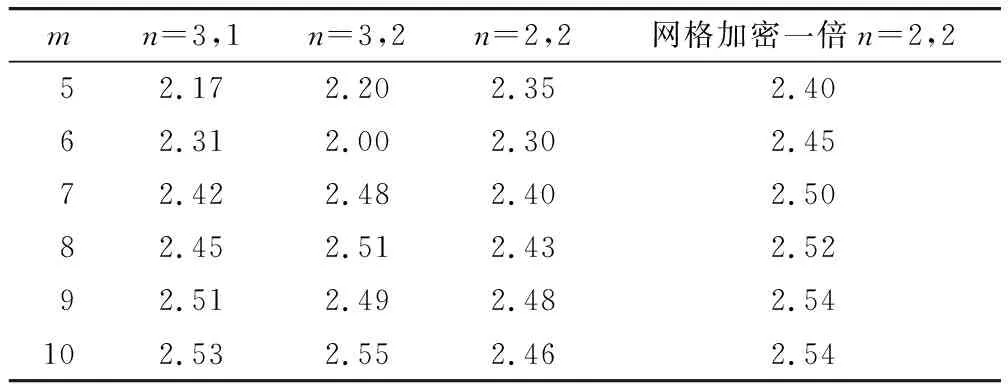
表3 應力強度因子
表3計算結果表明:采用圖6所示計算網格,當m≥7時,周邊數值覆蓋階數取2、3的多項式階數時,計算結果與理論值比較符合。當m≤7,計算結果與理論值有一定差別,局部數值出現跳躍,表明裂紋附近的網格還沒有達到足夠的密度。當網格加密一倍后,周邊數值覆蓋階數均取2階,當m≥7時,計算值與理論值十分接近,且隨著階數的提高,計算結果趨于穩定。
以上算例驗證了三維裂縫計算公式和程序的正確性,表明裂紋尖端解析解覆蓋和周邊數值解覆蓋聯合應用求解三維線彈性斷裂力學問題可行。與常規有限元方法相比,無需在裂紋尖端布置細密的網格,計算精度高,收斂相對較快。
裂紋尖端獨立覆蓋的密度、解析覆蓋的級數以及相鄰數值覆蓋的階數是影響應力強度因子計算精度的重要因素,但在保證獨立覆蓋有一定密度的情況下,提高與獨立覆蓋相鄰數值覆蓋的階數可以得到應力強度因子的精確解。
裂紋尖端獨立覆蓋的合理布置對應力強度因子的計算精度及穩定性有一定的影響,因此,下一步要重點研究裂紋尖端附近的覆蓋自動布置及密度問題,以保證方法的收斂性,便于開展三維裂縫擴展的動態模擬研究。
5 結論
將裂紋尖端解析解覆蓋和周邊數值解覆蓋聯合應用,分析三維線彈性斷裂力學問題,得到以下主要結論:
1)在包含裂紋尖端的解析覆蓋中,應用裂紋尖端附近的Williams位移解析解作為覆蓋函數,并采用高階多項式三維覆蓋函數與解析覆蓋的條形連接技術,實現了在解析覆蓋中直接求得裂紋尖端的三維應力強度因子。
2)典型的張開型和撕開型的裂紋算例表明,應力強度因子的計算精度較高。鑒于三維裂縫擴展問題的復雜性,裂紋尖端周邊數值覆蓋階數以及獨立覆蓋網格密度對應力強度因子計算精度的影響較二維問題更大。因此,協調獨立覆蓋密度、階數與周邊三維數值覆蓋階數的關系,來保證高精度求解收斂性的快速、穩定是下一步研究的重點。
考慮到解析級數是裂尖附近真實位移場的最佳逼近,相比其他方法而言,可以認為該方法在應力強度因子求解方面逼近效果更好、收斂更快,同時,由于網格布置根據不同區域的精度要求,只在裂尖附近進行覆蓋加密,因此,相比采用均勻網格的擴展有限元而言,計算效率將有所提高,可以實現大規模計算。另外,應力強度因子SIF本身就是裂尖解析級數的未知數,在求解系統方程組時一并得到,而不需要像其它方法那樣通過所謂的“直接”法或“間接”法來推求,不僅方便,而且不會引入額外誤差,這也是該方法的優勢所在。
該方法可以同時求解Ⅰ型、Ⅱ型、Ⅲ型(撕開型)裂紋的應力強度因子,應用復合型裂紋擴展準則就可以判斷其是否繼續開裂,因此,該方法在三維裂縫擴展的動態模擬方面極具應用前景。

