涵道式垂直起降固定翼無人機縱向穩定性研究

王春陽, 周洲, 王睿, 王科雷

(西北工業大學 航空學院, 陜西 西安 710072)

涵道式垂直起降固定翼無人機是一種復合型無人機，它既有直升機的垂直起降、空中懸停、低空低速飛行性能，又有固定翼飛機的高度巡航性能，它兼具了直升機和固定翼飛機的優點，是無人機發展的一個方向。它優異的性能和良好的經濟性在軍事領域和民用領域都有重要作用，具有廣闊的發展前景[1]。

涵道式垂直起降無人機有3種飛行狀態：起降懸停狀態、水平飛行狀態和過渡飛行狀態。為了滿足垂直起降和水平飛行，又能在兩者之間進行過渡飛行的要求，其自身過渡的穩定性問題就必須解決。由于過渡過程中飛行器構型不斷變化，為實現平穩過渡，各種動力單元共同參與，此時必須考慮過渡轉換過程中合理的動力分配、合理的速度范圍，保證無人機升力滿足飛行需求，以及過渡過程中動力單元和飛行姿態是連續變化的，因此過渡飛行狀態是垂直起降無人機最復雜的飛行狀態。為保證過渡飛行安全就必須確定飛機的過渡飛行走廊和飛行穩定性，使得飛行器在過渡走廊內安全過渡飛行。此外，建立這種涵道式飛行器動力部件的數學模型和整機的動力學模型時，如何準確地描述其過渡飛行運動，也是該類飛行器研究的重點。

涵道式飛行器有著特殊的構型，由于設計方案普遍動力配置充足，在過渡穩定性方面有較少的研究。在垂直起降方面，諸多學者進行了研究，包括氣動特性計算、動力學建模、飛行性能等方面。Leishman和Ananthan對共軸雙旋翼升力風扇進行了理論計算模型研究，運用葉素動量理論建立了共軸對轉雙旋翼的氣動力計算模型，通過理論模型研究了共軸對轉風扇的上下轉子的最佳葉片匹配[2]。鄭志成等參考涵道風扇動量理論模型, 建立了針對垂直起降飛機總體設計中關于升力風扇的估算模型，并通過具體算例對其進行驗證[3]。Yuksek等建立了升力風扇式垂直起降無人機六自由度非線性方程，并根據建立的數學模型進行了仿真計算模擬[4]。史小明以傾轉旋翼飛行器為研究對象，對其進行了縱向的飛行器建模，建立了飛行器氣動部件的氣動模型，并根據建立的縱向模型進行了配平和過渡階段穩定性分析[5]。曹蕓蕓以傾轉旋翼飛行器為對象，研究了傾轉走廊包線的確定方法，建立了動力學模型，根據模型對案例進行了分析計算，并根據飛行器特點研究了傾轉旋翼的操縱策略以滿足懸停和小速度飛行和過渡飛行模式[6]。萬華芳建立了傾轉旋翼飛行器的動力學理論模型，對過渡走廊進行了仿真研究[7]。高陽等對垂直/短距起降飛機進行了非線性動力學模型的建模[8]。符大偉等對升力風扇系統進行了較為詳細的實時數學模型建模[9]。此類研究注重傾轉旋翼類飛行器和升力風扇類飛行器的動力學建模和過渡走廊研究，本文將針對涵道式垂直起降無人機進行動力部件基于實驗數據的動力建模和全機動力學建模以及縱向穩定性研究。

1 涵道式垂直起降固定翼無人機

此類垂直起降無人機動力系統由共軸對轉升力風扇和推力涵道組成，升力風扇位于機體重心之前，推力涵道位于機翼后緣。垂直起降無人機主要氣動部件包括對轉升力風扇、左右增升涵道、左右控制 翼面和主機翼。文中整機的氣動力建模采用機體軸系OXbYbZb,如圖1所示,該軸系的原點位于飛行器的重心,x軸沿機體構造對稱面指向前,y軸垂直于x軸向右,z軸由右手法則確定向下,x軸與z軸構成了機體的對稱面[10]。氣動部件建模以氣動部件體軸系為基準。

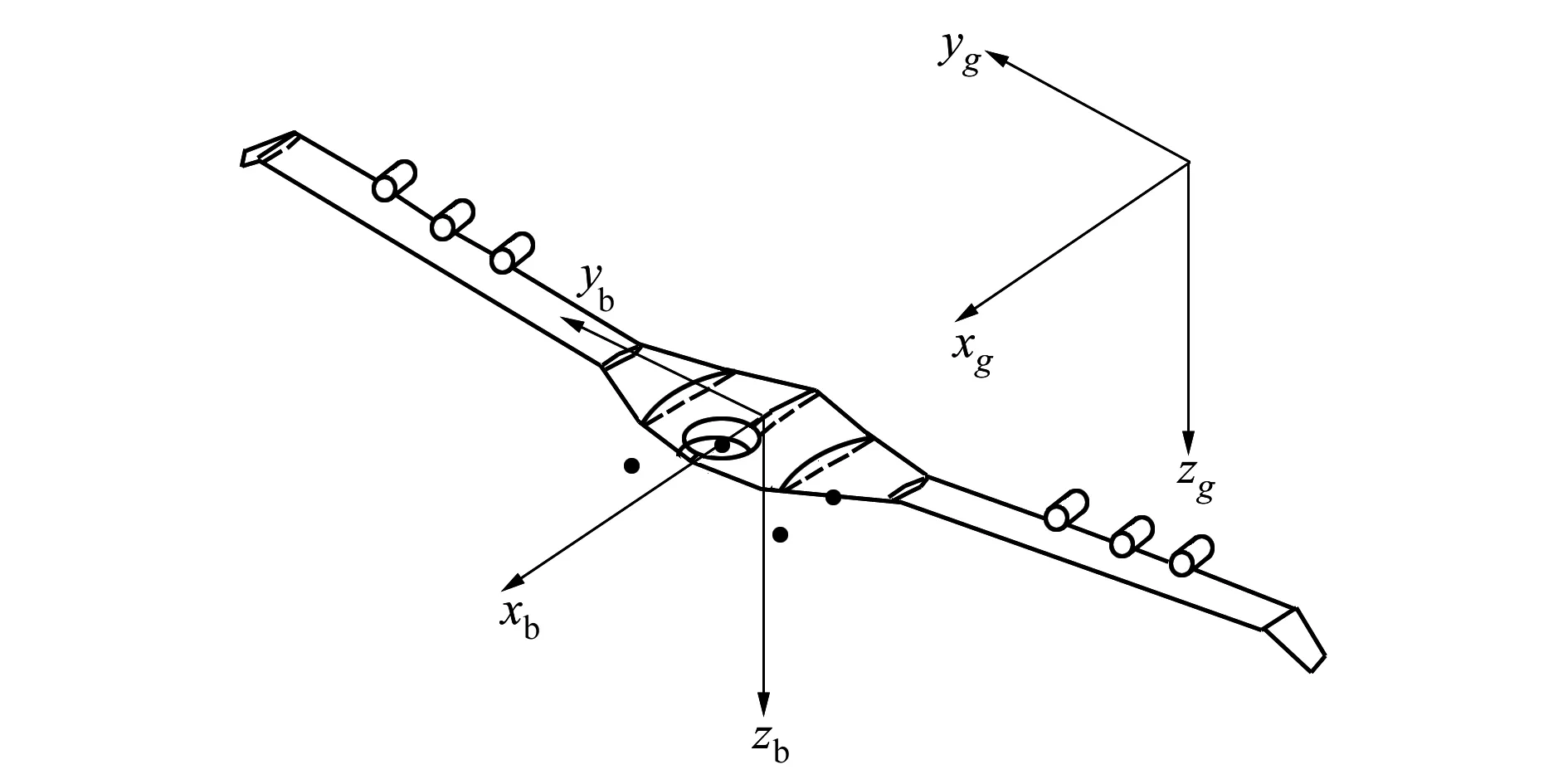
圖1 涵道式無人機坐標系

方案無人機從起飛懸停到過渡飛行過程如圖2所示,其中垂直起降時通過涵道偏轉提供向上的推力與前方的升力風扇一同產生推力使得無人機能夠垂直起降;過渡過程中通過偏轉涵道傾角來獲得前飛的推力,在一定的控制策略下能過完成從垂直起飛到水平飛行的過渡;在水平飛行時,涵道偏轉至水平,通過控制舵面的偏轉來控制飛行姿態。

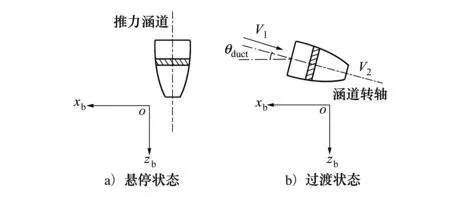
圖2 不同飛行狀態的涵道偏轉

2 氣動部件建模

涵道螺旋槳與孤立螺旋槳相比,在相同功率下,相同槳盤直徑時，可產生較大的拉力,即在相同功率下,產生相同拉力所需直徑更小。涵道螺旋槳產生這種差異的機理是:

1) 涵道的存在改變了螺旋槳下游的滑流狀態,增大了滑流面積,減小了滑流速度和滑流動能損失,從而較多地將螺旋槳槳盤后的動能轉化為壓力能。

2) 涵道壁面改善了螺旋槳槳尖區域的擾流特性,減少了擾流損失。

3) 涵道的入口前緣形成較大的負壓區,產生附加拉力。

共軸對轉升力風扇是由一對螺旋槳組成,上下分布,繞同一根軸轉動,但是旋轉方向相反。共軸對轉槳有以下優點:

1) 共軸對轉,使得發動機傳給飛機的反作用力矩減小到零。

2) 在最大飛行速度Vmax狀態下,共軸螺旋槳的總效率要比其總葉數目相等、飛行條件(來流速度V0,螺距H,轉數n,槳葉數N和槳半徑D)相同的非共軸螺旋槳效率高。

3) 高速飛行時,共軸螺旋槳的效率比具有相同任務的2個孤立螺旋槳效率高。

4) 共軸螺旋槳的起飛性能(在原地的拉力)要比單獨螺旋槳要好[11]。

目前尚無帶涵道的共軸雙旋翼空氣動力理論可供參考,本文基于共軸雙旋翼數學模型的計算數據和實驗數據,通過引入涵道唇口拉力修正系數η的方式,給出共軸雙旋翼涵道風扇的動力學模型。

2.1 升力風扇氣動力模型

本文采用葉素動量理論(blade-element moment theory,BEMT)[12]計算共軸雙旋翼的升力、功率以及力矩,由于文中飛行穩定性側重于升力和力矩,而對轉槳升力風扇力矩基本可以相互抵消,所以氣動力部件建模重點為升力的建模。計算公式采用NASA提出的無量綱形式[11]:

T=ρA(ΩR)2CT

(1)

共軸對轉雙旋翼系統的流動模型如圖3所示。基本假設是下旋翼部分槳盤面積工作在上旋翼的尾流區域,并且上旋翼尾流在進入下旋翼槳盤之前滑流速度在頸縮截面處有一個大的改變。尾流的收縮基于理想流體流動假設,或者通過特定的實驗數據支持。

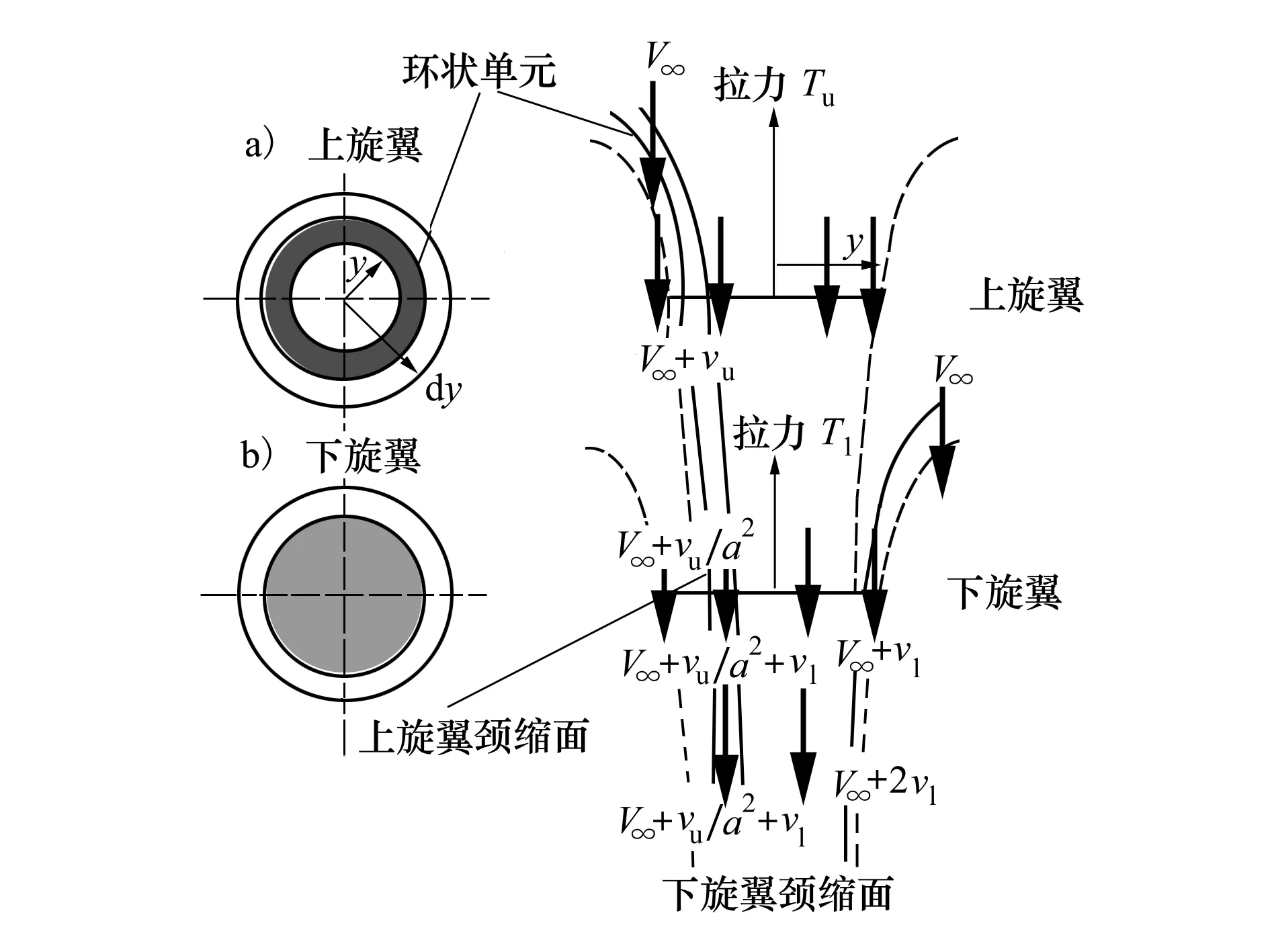
圖3 共軸對轉旋翼葉素動量理論分析模型

BEMT模型假設是上旋翼的滑流(流出)影響了下旋翼的滑流(流入),而下旋翼不會對上旋翼產生誘導影響。葉素動量理論可以用軸向自由來流速度進行一般性地推廣,自由來流速度一般記為V∞。

首先考慮共軸對轉系統的上旋翼,動量理論可以較好地解釋通過旋翼環狀面積的質量流量和誘導速度導致的推力增加。通過旋翼環狀面積的質量流量速度表示為[13]

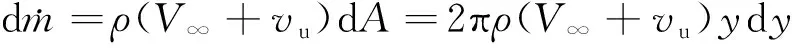
(2)

式中,dA=2πydy,那么環狀面積上增加的推力為

dTu=2ρ(V∞+vu)vudA=4πρ(V∞+vu)vuydy

(3)

將推力轉化為編撰的無量綱形式,上述方程可寫為

(4)

式中,λ=v/ΩR,λu=vu/ΩR,λ∞=V∞/ΩR,r=y/R代表無量綱的徑向位置。因此環狀面積的拉力系數可以寫為

dCTu=4λλurdr=4λ(λ-λ∞)rdr

(5)

BEMT中的槳尖損失可以通過普朗特槳尖損失方程進行計算,槳尖損失修正因子F的表達式如下

F=(2/π)cos-1(exp(-f))

(6)

式中,f通過葉片數目Nb和葉片單元的徑向位置r給出,表達式如下

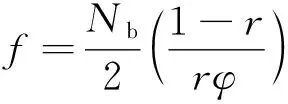
(7)

式中,φ=λ(r)/r是小角度假設下的入流角。那么普朗特槳尖損失方程修正的環狀面積拉力系數表示為

dCT=4Fλλurdr

(8)

運用經典葉素理論,槳盤上相同環狀面積的所產生的拉力表示為

(9)

式中:θu是指上旋翼的葉片扭轉角,可能包含了葉片截面的零升力迎角;σu為槳盤實度。將經典葉素理論與葉素動量理論所獲得的拉力系數進行聯立求λ的方程,可得

(10)

式中,λu=λ-λ∞。上式在槳盤一系列離散單元上可以得到數值解。

同樣的數學原理可以應用于下旋翼的分析。根據前面的假設,下旋翼一部分工作在上旋翼的滑流區域,在理想狀態下,根據流管收縮可以求得頸縮面積Ac=πa2R2,其中a=0.707,Ac/A=0.5。可求得下旋翼上方的頸縮截面流速為V∞+vu/a2。

與上旋翼的計算方法類似,受上旋翼滑流影響區域(r≤a)的下旋翼流速可求得

(11)

式中:θl是指下旋翼的葉片扭轉角,λl=λ-λ∞。

對于沒有受到上旋翼滑流影響的區域(r>a),流速計算如下

(12)

方程(10)～(12)給出了上下旋翼各個離散徑向位置在任何葉片槳距、葉片扭轉以及翼型截面情況下的流速近似計算方法。

根據上述拉力系數計算公式以及流速計算公式,旋翼的拉力、功率和扭矩就可以對每個槳盤進行數值積分來獲得。上旋翼、下旋翼和總拉力系數表達式如下

本文在上文中BEMT理論建立的共軸雙旋翼氣動力模型基礎上，提出了基于CFD數據與實驗數據的共軸雙旋翼涵道升力風扇空氣動力學模型。涵道和唇口的存在,一定程度上影響了上旋翼的誘導速度,而對下旋翼的氣動力幾乎沒有影響,因此對上旋翼的誘導速度λ通過CFD數據和實驗數據進行了修正,修正系數為η。氣動部件的氣動力是通過BEMT進行積分計算得到的,在數值計算方面有較好的應用,但是對于升力風扇氣動力的解析式是相當復雜的,因此文中提出了運用特征截面的氣動數據來表達整體氣動數據的方法。同樣根據CFD數據和實驗數據進行了數據修正,以螺旋槳r/R=0.6處的截面參數為升力風扇計算的特征截面參數。

圖4 升力風扇

升力風扇在飛行器運動過程中其遠場速度與飛行器的飛行參數密切相關,具體可表達為

V∞=-Vz+qLfanG

式中：Vz為飛行器z向速度；q為俯仰角速率；LfanG為升力風扇中心到飛行器重心的水平距離。由公式(10)結合實驗數據加以修正得出上旋翼的無量綱誘導速度

(16)

其中特定涵道唇口的修正系數為η=f(V∞)。特征截面處的上旋翼拉力系數為

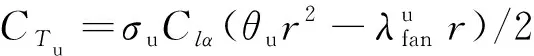
(17)

對于下旋翼無槳尖修正的無量綱誘導速度,由于涵道壁的影響,下旋翼基本不存在頸縮現象,即公式(11)頸縮系數a=1,由此計算下旋翼無量綱誘導速度

(18)

特征截面處的下旋翼拉力系數為

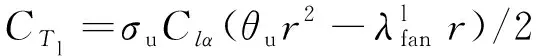
(19)

2.2 推力涵道氣動力模型

與升力風扇類似,運用BEMT理論,建立推力涵道的氣動力模型,其中推力涵道屬于多葉片高轉速涵道,其葉片弦長從根部到尖部基本保持不變,其葉片槳尖損失較小,這一點與升力風扇建模有所區別。并且,涵道存在轉子葉片和定子葉片,即下葉片不轉動,模型的等效拉力由上旋翼轉子產生,同樣運用CFD數據和實驗數據進行模型修正,其計算方法如下。

圖5 推力涵道

推力涵道上旋翼轉子誘導速度計算為(20)式,式中計算方法是在公式(16)的基礎上去掉了槳尖修正系數F得來,其推力涵道對應的遠場速度可表示為V∞=-(Vz+qLductG)sinθd+Vxcosθd。

(20)

特征截面處的上旋翼拉力系數計算為

城市旅游效率時空格局會受到資源、經濟市場結構以及政策等各種因素的影響，這些因素會推動空間格局不斷變化、演化。不同區域的作用機制就是時空格局發展的內在驅動力。根據研究以及理論分析，綜合分析變量的代表性以及數據的可獲取性，其主要的影響因素主要有旅游資源稟賦(RES)、旅游接待設施規模(TF)、城市基礎設施條件(PTlJ)、產業結構(STR)、外貿依存度(TRA)、政府規模(GOV)等幾點因素。

(21)

3 飛行動力學建模

對于存在涵道偏轉的剛性無人機,六自由度方程可以較好地描述其飛行運動,其動力學模型滿足方程(22)～(23)。合外力F由飛行器各部件的空氣動力和重力組成,用Fx,Fy,Fz表示空氣動力在機體軸系下的三分量,∑M為外力對機體坐標系原點的力矩之和。將機體軸系下的全量方程在基礎運動的條件下進行線化處理,可以得到飛行器線化運動方程[14]

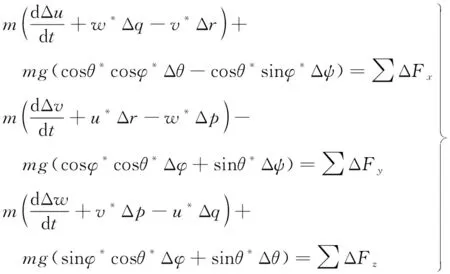
(22)

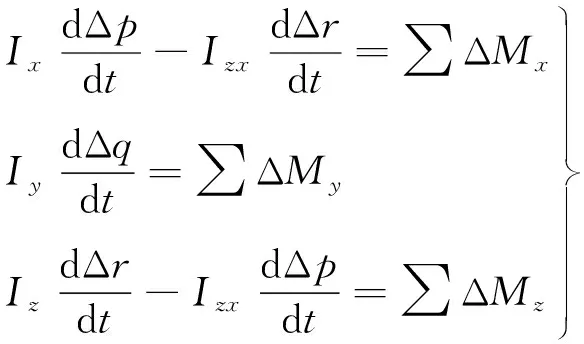
(23)

(22)～(23)式中等號右邊為擾動引起的空氣動力和力矩的變化,除了前面提到的運動參數擾動外,操縱人員的操縱也是引起無人機空氣動力和力矩變化的擾動因素,但文中重點研究無人機的自身穩定性,認為飛行器在研究范圍內無操縱穩定飛行,那么空氣動力和力矩的小擾動表達式為

式中,?Fx/?u,…,?Fx/?r為氣動導數,其值按照基準飛行狀態的飛行參數來確定,與擾動運動中的參數變化無關,同樣∑ΔFx,…,∑ΔMz的小擾動表達式與之類似。

根據機體軸系形成過程可以求得機體旋轉角速度在機體軸系上的投影,進而可以求解出姿態角與角速度之間的運動學關系方程,最終按小擾動條件進行線化處理,可以得到飛行器的小擾動線化運動學方程組[15]

(24)

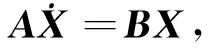
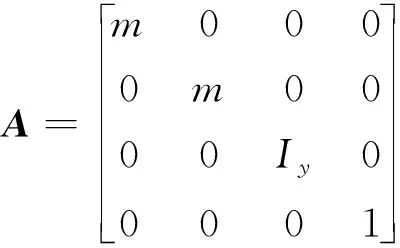
(25)

(26)

4 案例無人機縱向穩定性分析

4.1 平衡方程及求解

4.1.1 懸停平衡

垂直起降無人機在懸停階段,作用在其上的力和力矩如圖6所示。在懸停過程中,只有升力風扇和增升涵道作為動力,機翼不提供氣動力,在機體軸系下建立無人機力和力矩縱向平衡方程。

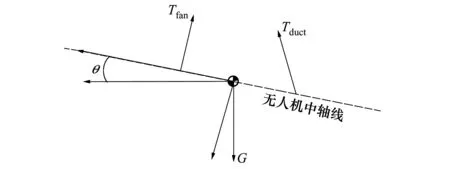
圖6 無人機懸停受力分析

(27)

式中：m為全機質量；l為作用力臂長度；θ為俯仰姿態角。

在一定俯仰姿態角θ下求解方程組(27)可得在懸停平衡狀態下的升力風扇推力Tfan,推力涵道推力Tduct和推力涵道偏轉角θduct。

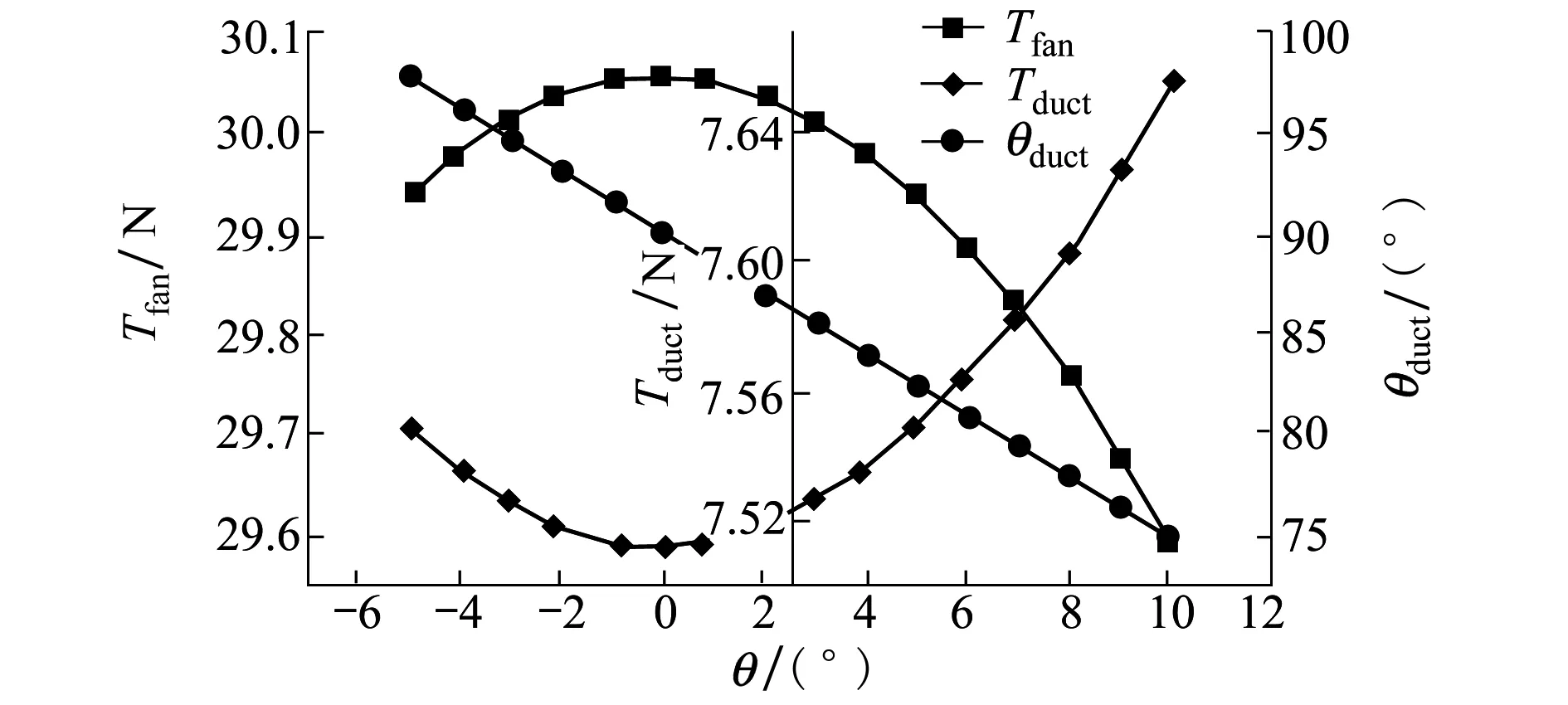
圖7 懸停配平結果

4.1.2 過渡平衡

在過渡平衡狀態下,力學方程較懸停平衡狀態多了自由來流在機體上產生的氣動力和力矩,懸停受力示意如圖8所示。

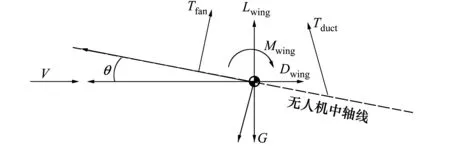
圖8 無人機過渡受力分析

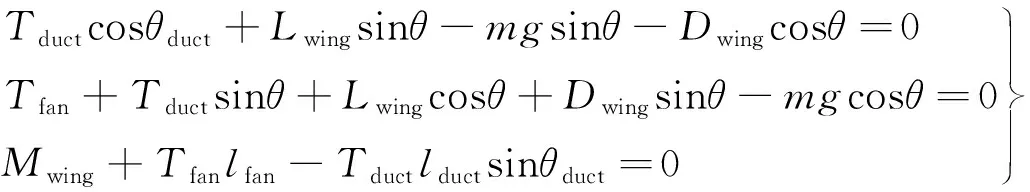
(28)

式中：L為升力；D為阻力；M為力矩。

方程組(28)在一定過渡姿態俯仰角下,求得不同速度下的過渡平衡的升力風扇推力Tfan,推力涵道推力Tduct和推力涵道偏轉角θduct,如圖9所示。

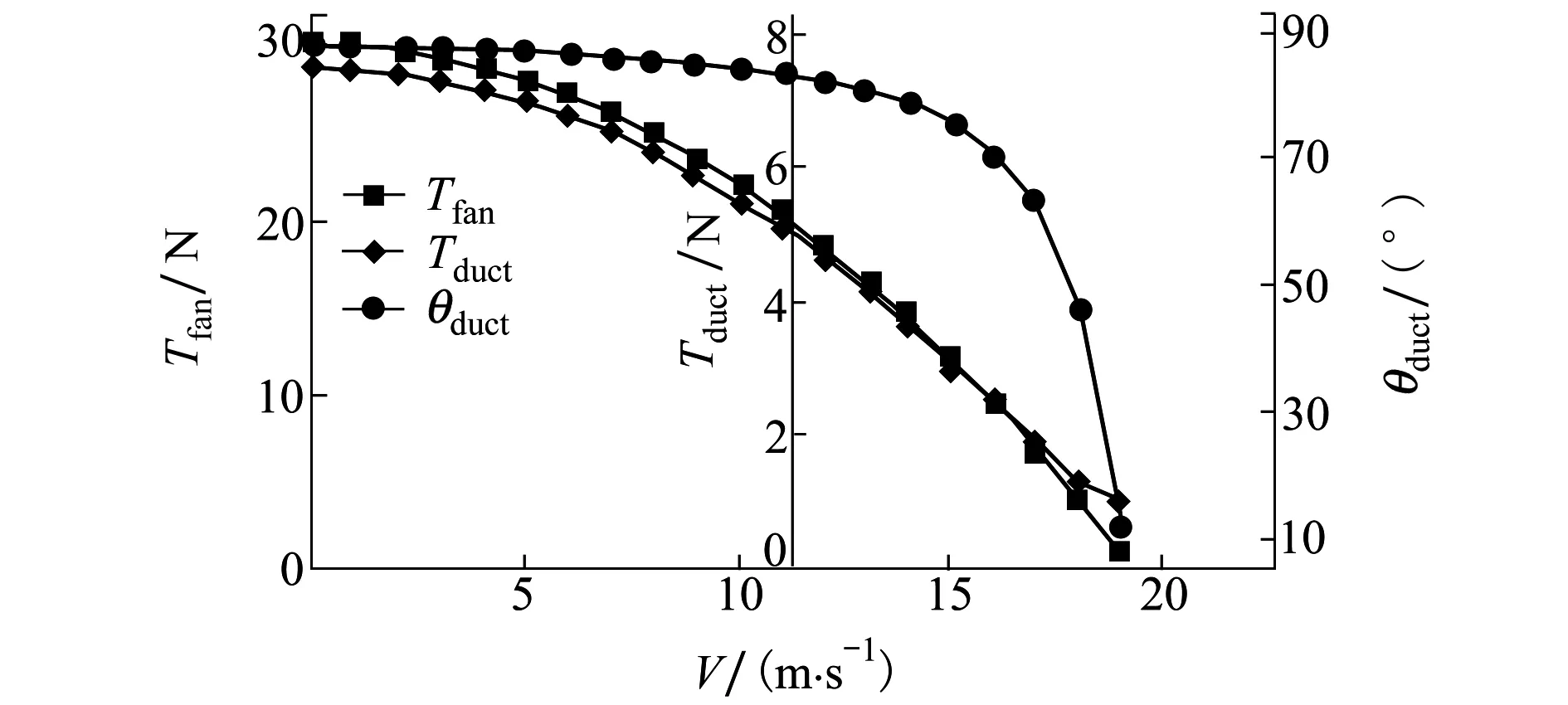
圖9 過渡配平結果

4.2 縱向穩定性

通過本文升力風扇計算模型和推力涵道計算模型,可以在不同轉速下、不同來流速度的推力。模型計算與CFD計算和實驗數據比較接近,誤差在5%以內,將3種數據集中在圖10中,能直觀地看出數據吻合度,證明了文中建立模型的準確性。

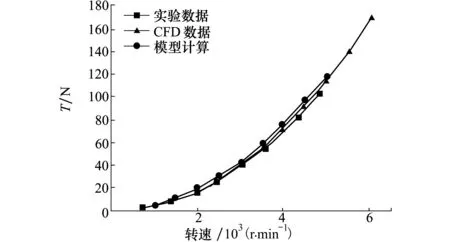
圖10 升力風扇數據對比

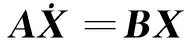
由懸停特征根分布圖11可以看出,只有在俯仰姿態角為0°的時候,其縱向穩定性表現出2個零根和2個不同的負實根,其縱向穩定性表現為中立穩定模態和單調收斂模態;當無人機懸停姿態角小于零時,其存在一對實部為正的共軛復根,振蕩發散,同時存在一正實根和一負實根,致使系統處于發散狀態;同樣當懸停俯仰角大于零的時候,存在一對實部為負的共軛復根和2個正實根,存在振蕩收斂長周期模態和單調發散運動。在整個懸停姿態角范圍內,根據四次特征方程的Routh-Huewitz穩定性準則判定,其在懸停過程中縱向表現為不穩定。

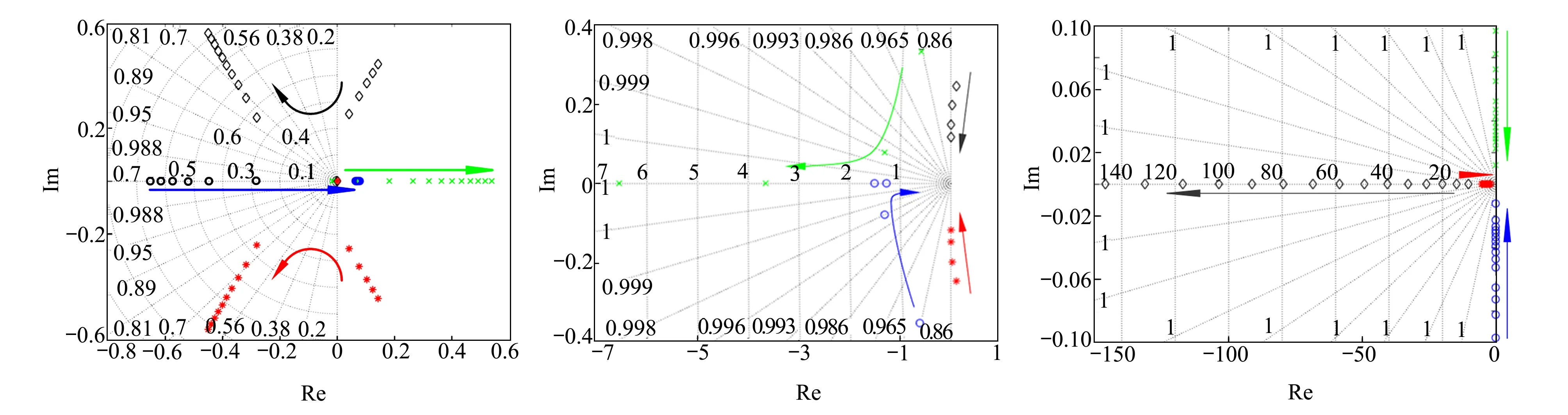
圖11 懸停根軌跡變化 圖12 速度1～4 m/s縱向根軌跡圖13 速度5～20 m/s縱向根軌跡

過渡過程中總的氣動力比懸停過程中多了機身氣動部件產生的氣動力,其氣動導數可以通過CFD計算軟件求得,在固定姿態角的過渡過程中,隨著過渡速度的增大其縱向特征根變化如圖12～13所示。圖12為過渡速度從1～4 m/s時的縱向特征根變化趨勢,根據特征根表現和勞斯判據可知在這個過渡速度期間,其縱向穩定性為不穩定狀態。當速度大于5 m/s時,其特征根表現為圖13,其特征根表現為2個實部為負的復根和2個負實根,表現為長周期模態和過阻尼模態特征,根據Routh-Huewitz判據可以知道在此過渡速度下其縱向穩定性為穩定狀態。

在懸停狀態下,根據飛行器吊掛試驗,在懸停狀態下,無控制參與的情況下,保持飛行器懸停,并給予初始縱向擾動,通過飛行控制器記錄反饋數據,如圖14所示,可以驗證俯仰擾動下的振蕩模態與本節懸停穩定性計算結果吻合。根據本節懸停特征根可計算得懸停狀態下其縱向振蕩收斂模態特征周期為100～101量級,在吊掛實驗飛行控制器采集數據端能夠較好地觀測其振蕩周期數據如圖15所示。在俯仰擾動中俯仰姿態角曲線振蕩周期可以計算得出,其收斂平均振蕩周期為7 s,與文中縱向穩定性計算結果中的振蕩模態特征結果基本保持一致,從而驗證文中穩定性計算方法在表述此飛行器縱向運動時的準確性。

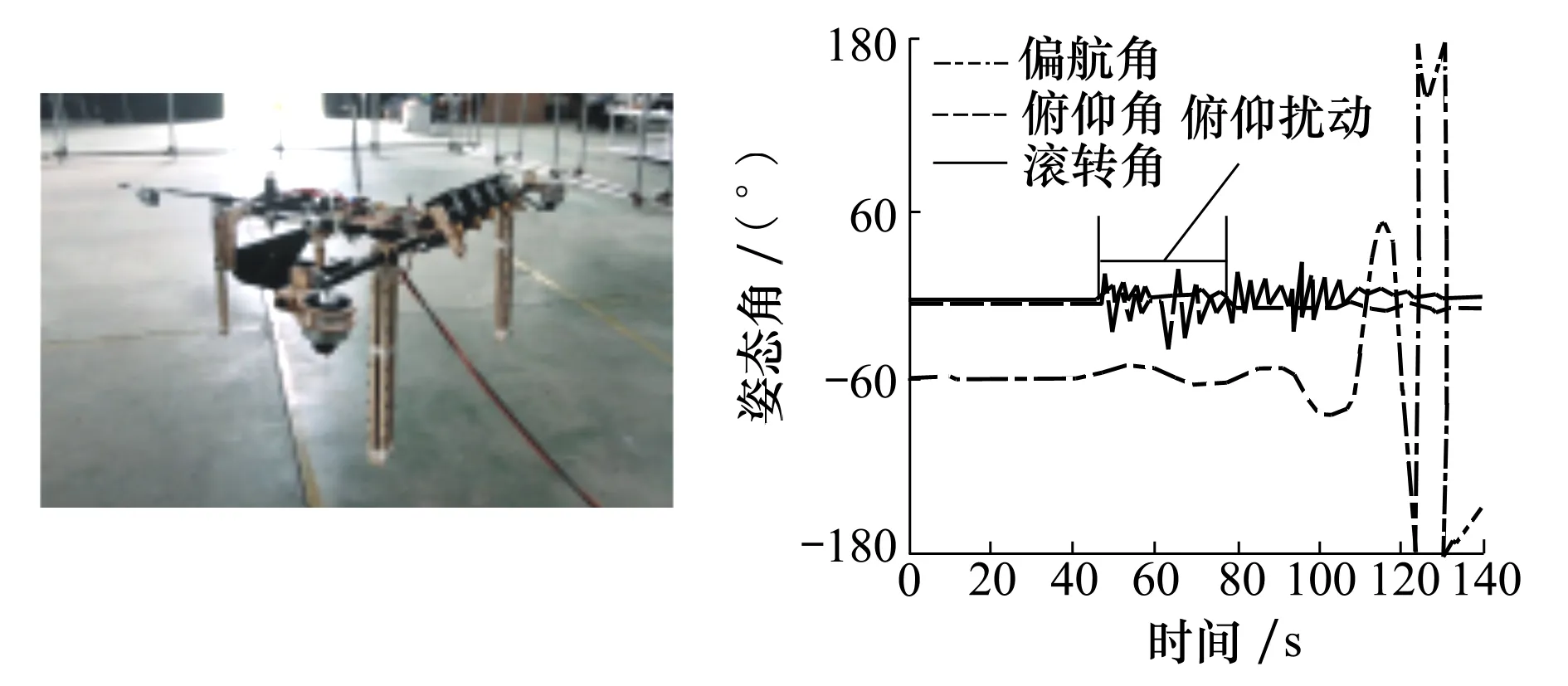
圖14 懸停吊掛實驗 圖15 懸停吊掛實驗曲線

5 結 論

本文通過葉素動量理論、實驗數據參數辨識方法、帶質量偏轉的六自由度方程和模態特征分析方法對涵道式垂直起降固定翼無人機進行了研究,可以得出以下結論:

1) 文中基于BEMT理論改善了帶唇口的共軸雙旋翼涵道的氣動力模型和推力涵道模型,基于特征截面計算的模型,解析式修正參數根據實驗數據辨識而來,此模型能夠較準確地描述升力風扇的動力,誤差在5%以內。

2) 以剛體六自由度方程為基礎建立了帶涵道質量偏轉的飛行動力學模型,推力涵道質量偏轉直接影響無人機的慣量,此模型能夠較完整地描述此類無人機縱向運動狀態。

3) 運用文中建模方法,基于模態特征,對案例無人機進行了縱向穩定性分析。在懸停狀態下,只有0°俯仰姿態角時,無人機存在中立穩定和單調收斂模態,其他姿態角懸停縱向擾動運動均為不穩定狀態。在過渡飛行時,在一定俯仰角下過渡,初始小速度1～4 m/s階段,由其縱向根軌跡和勞斯判據可知其為不穩定狀態;當速度大于5 m/s時,根軌跡表現為長周期模態和過阻尼模態,根據勞斯判據可知,在此狀態下無人機縱向擾動運動是穩定的。

文中圍繞此類涵道式固定翼無人機縱向穩定性進行了研究,下一步將在橫航向穩定性和全機操縱性方面展開研究。