基于多面體單元的三維ES-FEM理論研究

楊建, 謝偉, 張志偉

(1.西北工業大學 航空學院, 陜西 西安 710072; 2.液體火箭發動機技術國防科技重點實驗室, 陜西 西安 710100)

有限單元法(FEM)是一種通過將無限自由度問題離散為有限自由度，從而得到近似結果的高效數值算法，該方法自問世以來就在很多領域內得到了廣泛應用。目前對于三維有限元問題，四面體和六面體單元具有原理簡單、網格生成算法成熟等優點，被絕大多數商業軟件所采用。然而在面對大型復雜結構時，四面體網格計算精度差，六面體網格難以劃分等缺點也逐漸突出。

近年來，多面體單元由于其單元面的形狀和數量都具有任意性，為網格生成提供了巨大的靈活性等特點而受到廣泛關注[1-9]。然而因為難以構造滿足單元協調性的多項式形式的形函數以及網格生成算法不夠成熟，與常規有限元相比其發展仍然處于起步階段。

劉桂榮教授和Nguyen-Thoi創立了一系列的光滑有限元法(S-FEM)[10]，由最初的光滑子單元域有限元法(CS-FEM)[11]，之后推廣到光滑節點域有限元法(NS-FEM)[12]、光滑面域有限元法(FS-FEM)[13]和光滑邊域有限元法(ES-FEM)[14]。這些方法都具有一個共同的特點，即不需要對形函數求導，降低了形函數必須連續的要求，這一特點可以有效地解決使用多面體網格遇到的問題。

在以上這些S-FEM算法中，二維光滑邊域有限元法被證明具有最佳的穩定性和精度[14]。所以本文在二維ES-FEM基礎上，建立了基于多面體單元的三維光滑邊域有限元法，劃分了三維ES-FEM在多面體單元中的的光滑域，推導了幾何矩陣和剛度矩陣。通過Matlab軟件編制的計算程序計算了彈性力學典型三維算例，并將結果與常規有限元結果等進行了對比研究，證實了基于多面體單元的三維ES-FEM方法的可行性與可靠性。

1 ES-FEM-Poly的基本理論

在多面體網格中,ES-FEM-Poly以多面體單元的邊為基準,在與該邊相鄰的n個單元中劃分n個光滑子域,n個光滑子域組成了一個以該邊為基準的光滑域。本文研究的多面體為包括四面體,六面體在內的任意面體。圖1給出了以五面體單元為例的光滑子域的劃分方法,光滑子域由基準邊的2個端點B、D,鄰接單元面的形心F、G,鄰接單元的體心H組成的五結點六面體。在多面體網格中,一個邊的鄰接單元數量不定,所以組成一個光滑域的光滑子域數量也不定,模型中邊的數量等于光滑域數量。

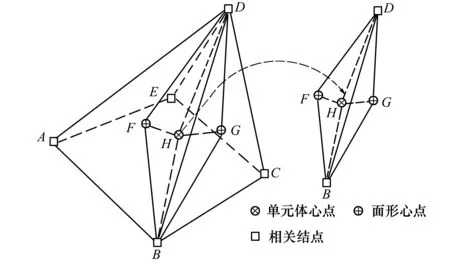
圖1 五面體單元光滑子域劃分方法

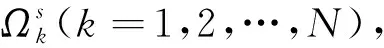
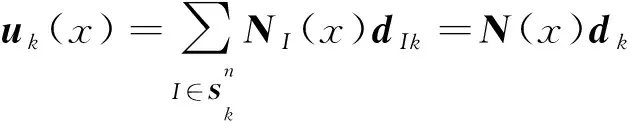
(1)

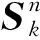
ES-FEM-Poly的形函數并不是關于相關結點位移的連續函數,不需要導數,針對這一特點使用線性插值法[15],直接計算相關結點在積分面上高斯積分點處的形函數值,將高斯積分點取為每個面的形心。以圖1所示的五面體為例,表1給出了對應的形函數值表。表中第i行第j列的值代表第i個結點在第j個相關結點處的形函數值。

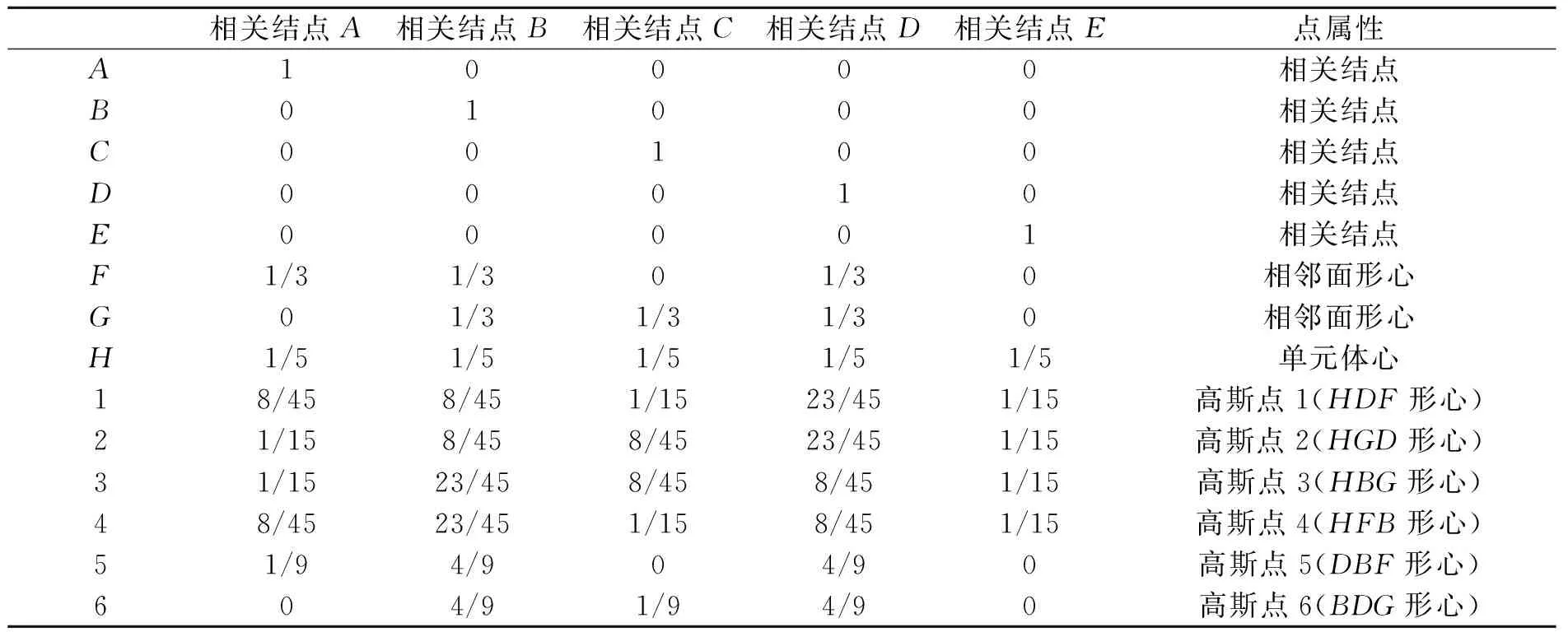
表1 形函數值表

對于一個擁有n個結點的多面體單元,每個結點在體心處的形函數值是1/n,在其他位置計算形函數的方法與五面體單元相同。

(2)

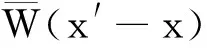
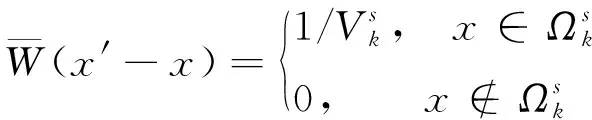
(3)

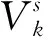
(4)

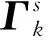
將(1)式代入(4)式中,可得

(5)

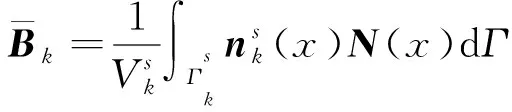
ES-FEM-Poly的總體平衡方程可由光滑Garlerkin弱化形式[13]得到

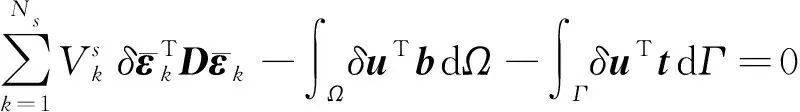
(6)

式中：b為體積力向量；t為邊界牽引力向量；D為彈性系數矩陣。

將(1)式和(5)式代入(6)式并簡化可得

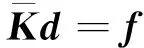
(7)

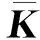
(8)

接下來,將每個光滑域的剛度矩陣按照常規有限元方法組裝成整體剛度矩陣,然后求解平衡方程。

從以上推導過程可以看出,ES-FEM-Poly對光滑域的邊界進行積分而無需對光滑域積分,從而無需像常規有限元那樣對坐標進行映射,它只要求多面體單元任意邊的2個結點與單元形心所組成的三角形面必須位于單元內部,因此大大降低了對網格質量的要求,即使是單元內兩相鄰面內角大于180°的畸形網格也同樣能滿足要求。

2 算例分析

本文利用Matlab軟件編寫了ES-FEM-Poly算法程序,計算了空心球模型和懸臂梁模型,將計算結果與常規有限元四面體單元(FEM-T4)和六面體單元(FEM-H6)所得結果通過應力相對誤差和能量相對誤差進行比較。

應力相對誤差

(9)

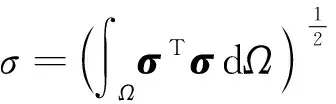
能量相對誤差

(10)

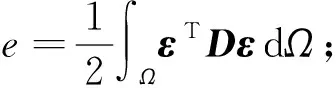
由于本文所用網格類型不同,且形狀不規則,引入單元特征邊長來表征網格疏密程度。

(11)

式中：VΩ,Ne分別為整個模型的體積和單元個數。

2.1 空心球模型

空心球內外半徑分別為a=5 m,b=10 m,彈性模量E=72 GPa,泊松比μ=0.33,因其對稱性,仿真計算時只取1/8模型,在其內表面施加P=100 MPa的壓力,在其3個對稱面上分別施加x,y,z方向的位移約束,如圖2所示。

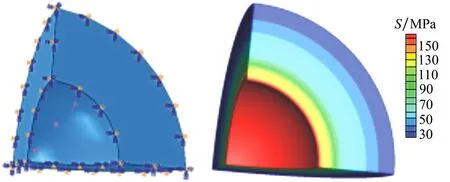
圖2 1/8空心球模型示意圖 圖3 球模型參考應力云圖

選取1 016 379個六面體單元網格計算所得結果為參考解,圖3給出了參考應力云圖,圖4給出了不同數量多面體單元對應的應力云圖。從圖中可以看出,應力分布隨著單元數量的增加越來越接近參考解的應力分布。

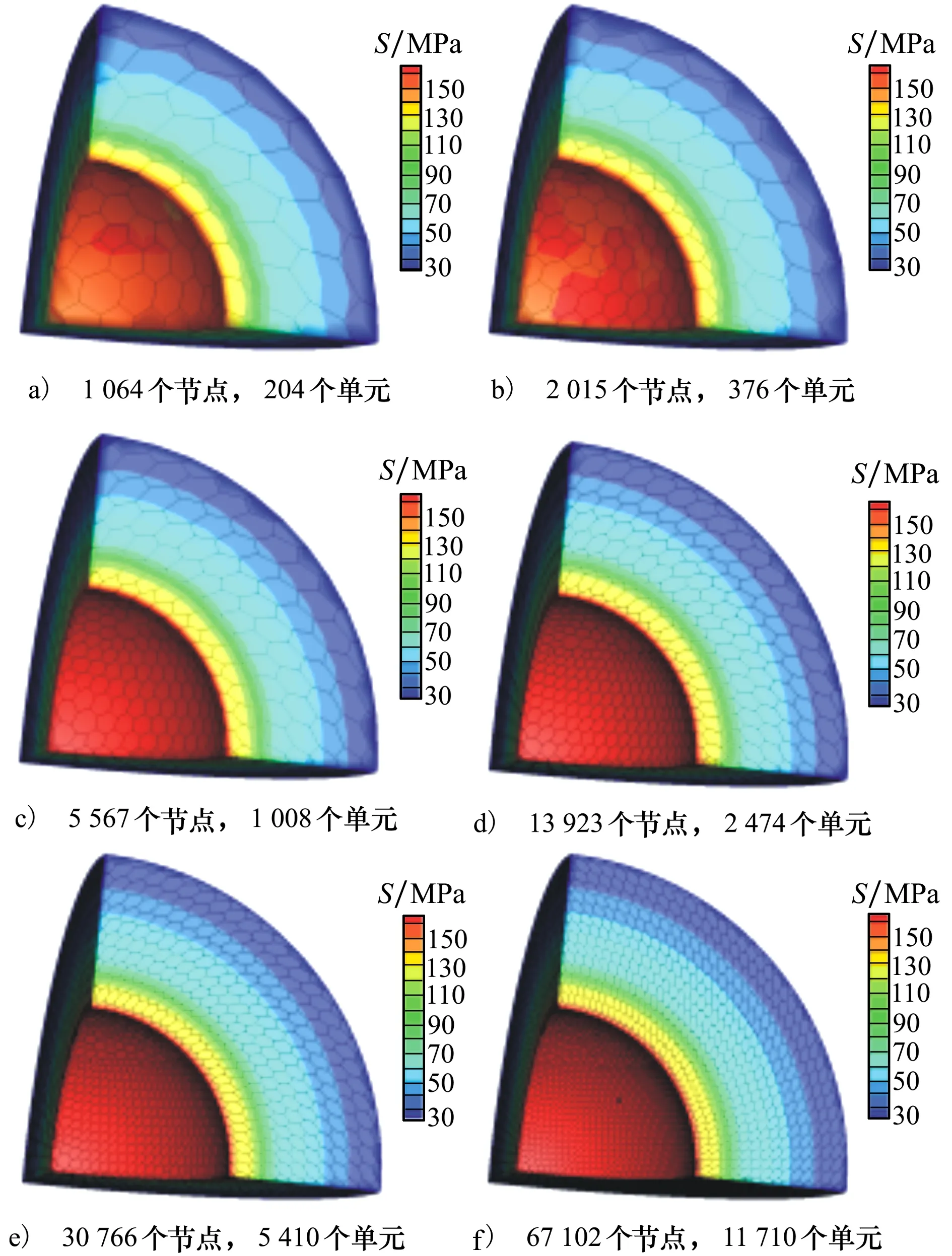
圖4 不同數量多面體單元的應力云圖

圖5給出了不同數值方法下應力相對誤差隨單邊特征邊長的收斂曲線。從圖中可以看出,3條曲線比較接近,表明不同方法應力誤差相差不大,但ES-FEM-Poly曲線的斜率明顯大于FEM-H6和FEM-T4的曲線斜率,表明：隨單元數量增加,lg(h)減小,ES-FEM-Poly計算結果更趨近參考解,表明其有更好的收斂性。當h<0.5 m，即lg(h)<-0.3時,ES-FEM-Poly的精度高于FEM-T4;當h<0.38 m，即lg(h)<-0.42時,ES-FEM-Poly的精度高于FEM-H6。

圖5 各算法的應力相對誤差收斂曲線

圖6給出了不同數值方法下能量相對誤差隨單邊特征邊長的收斂曲線。從圖中可以看出,ES-FEM-Poly和FEM-H6的精度相似,且高于FEM-T4;但ES-FEM-Poly曲線的斜率大于FEM-H6和FEM-T4的曲線斜率,表明ES-FEM-Poly的收斂性要比FEM-H6和FEM-T4好。

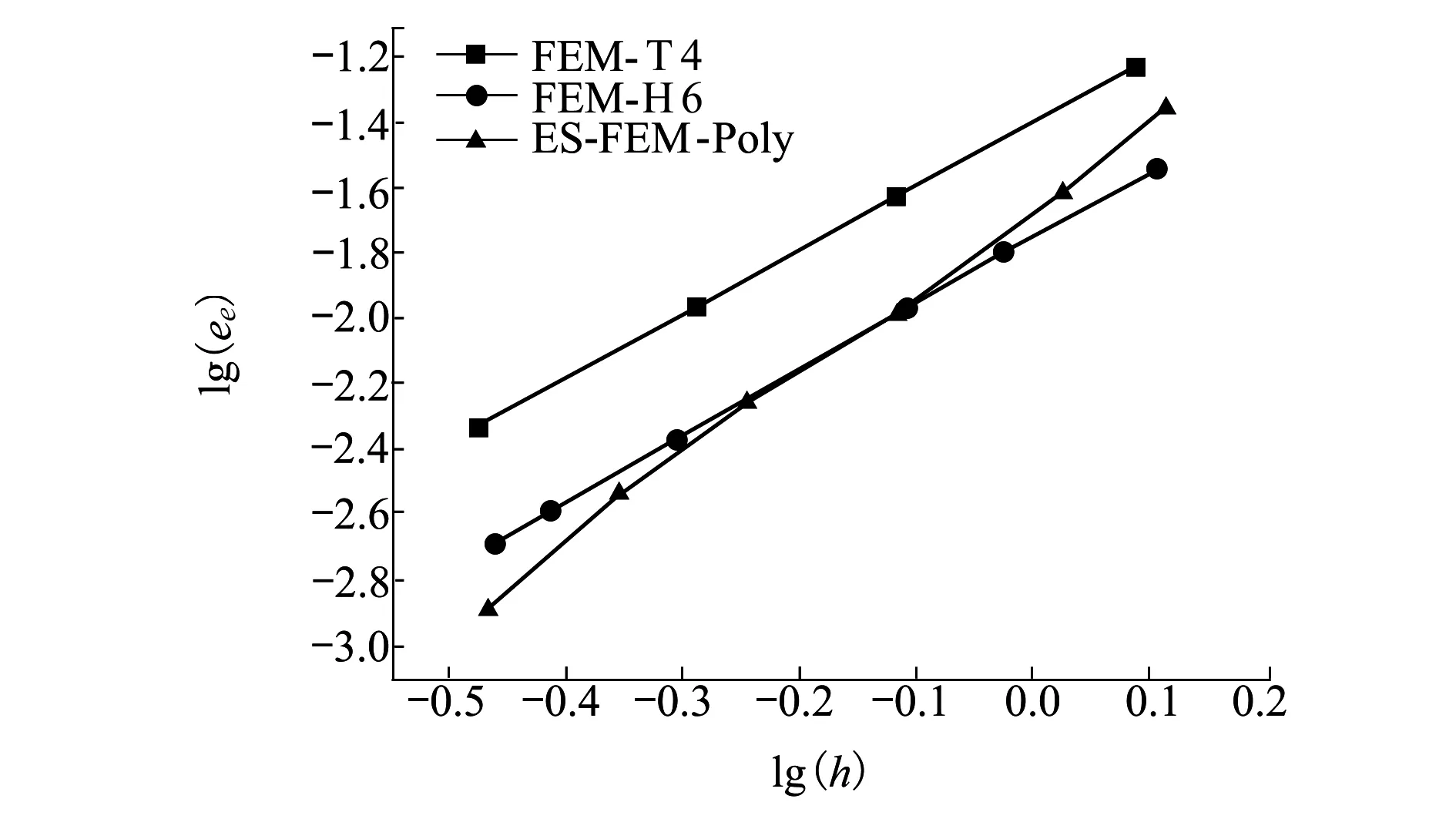
圖6 各算法的能量相對誤差收斂曲線

2.2 梁模型

如圖7所示,長和寬為5 m,高為60 m的三維懸臂梁模型一端固支,另一端受到方向沿Y軸負方向的10 MPa均布剪力。彈性模量E=72 GPa,泊松比μ=0.33。

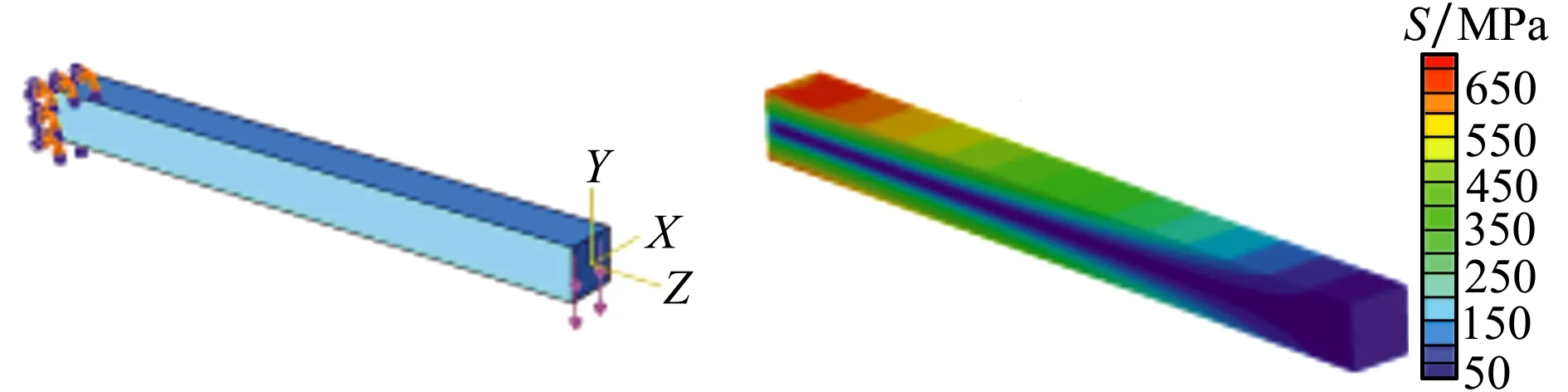
圖7 梁模型示意圖 圖8 梁模型參考應力云圖

選取2 976 750個六面體單元網格計算所得結果為參考解,圖8給出了參考應力云圖,圖9給出了不同數量多面體單元對應的應力云圖。從圖中可以看出,應力分布隨著單元數量的增加越來越接近參考解的應力分布。

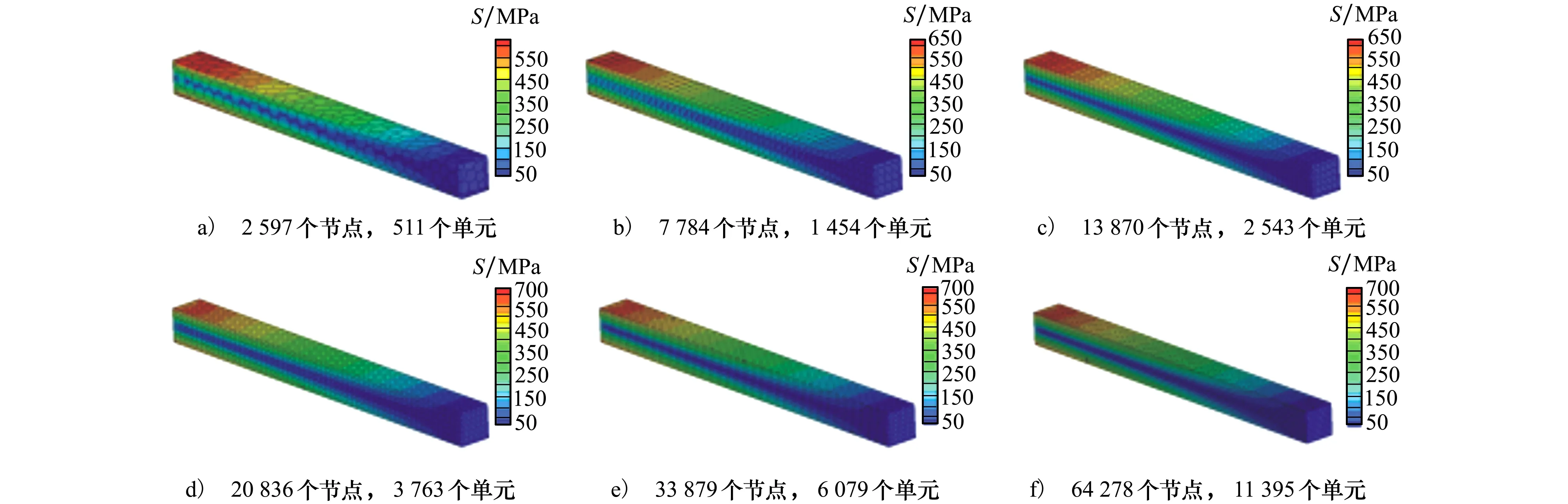
圖9 不同數量多面體單元的應力云圖

圖10給出了梁模型應力相對誤差隨單邊特征邊長的收斂曲線。從圖中可以看出,ES-FEM-Poly的曲線明顯低于FEM-T4和FEM-H6,表明ES-FEM-Poly的計算精度顯著高于FEM-T4和FEM-H6。當h=0.5 m，即lg(h)=-0.3時,ES-FEM-Poly的應力相對誤差是FEM-H6的1/4,是FEM-T4的1/6。

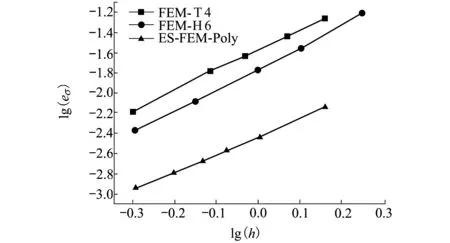
圖10 各算法的應力相對誤差收斂曲線

圖11給出了梁模型能量相對誤差隨單邊特征邊長的收斂曲線。從圖中可以看出,使用多面體單元的ES-FEM-Poly的計算精度與FEM-H6相近,但顯著高于FEM-T4。當h=0.5 m，即lg(h)=-0.3時,ES-FEM-Poly的能量相對誤差是FEM-T4的1/24。

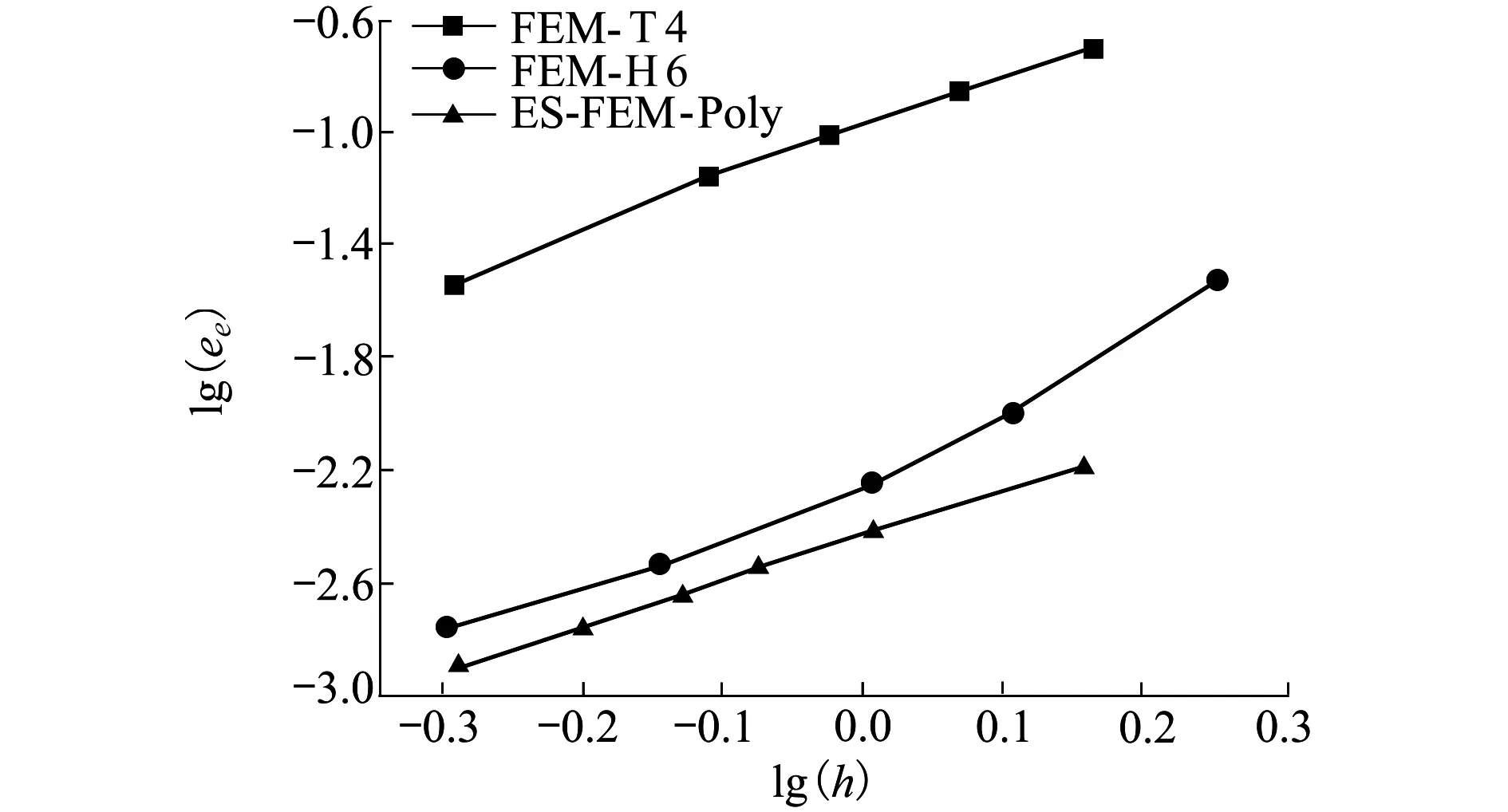
圖11 各算法的能量相對誤差收斂曲線

3 結 論

本文建立了基于多面體網格的光滑邊域有限元法,介紹了多面體單元的光滑域劃分方法、形函數的構造以及幾何矩陣和剛度矩陣的推導,利用Matlab軟件編程計算了空心球模型和梁模型,并將結果與常規有限元結果進行對比研究,可以看出：①ES-FEM-Poly曲線的斜率明顯大于FEM-H6和FEM-T4的曲線斜率,表明隨著單元數量增加,ES-FEM-Poly計算結果更趨近參考解,有更好的收斂性；②ES-FEM-Poly曲線明顯低于FEM-H6和FEM-T4曲線,表明在單元特征邊長一定時,ES-FEM-Poly計算結果更接近參考解,精度更高。

綜上所述，基于多面體網格的三維光滑邊域有限元法,相比于常規有限元方法具有更好的精度和收斂性,可以用該方法對結構復雜的三維彈性力學問題進行分析。