基于表征駕駛風格的駕駛員縱向加速度模型

王雪瑩，張譯芳，袁盛玥，馬世峰Wang Xueying ，Zhang Yifang，Yuan Shengyue，Ma Shifeng

基于表征駕駛風格的駕駛員縱向加速度模型

王雪瑩1，張譯芳1，袁盛玥1，馬世峰2
Wang Xueying1，Zhang Yifang1，Yuan Shengyue1，Ma Shifeng2

（1. 北京新能源汽車股份有限公司，北京 100176；2. 長春孔輝汽車科技股份有限公司，吉林 長春 130012）

駕駛員駕駛風格的差異會引起縱向加速度決策與最優值存在一定程度的偏差。改進了基于最優預瞄的駕駛員縱向加速度模型，以跟隨速度為參考量，提出了多點多目標的二階預瞄決策模型，并以預瞄視野、決策意愿和決策偏差表征駕駛員的駕駛風格進行建模。通過Simulink-Carsim聯合仿真，驗證模型可以反映出不同駕駛風格下的駕駛行為，為研究分析真實駕駛行為提供借鑒。

車輛工程；駕駛員模型；駕駛風格；二階預瞄

0 引 言

在人—車—路閉環系統中，駕駛員兼做道路狀況的感知環節和車輛操作的決策環節，感知處理著各種信息，對車輛安全穩定行駛以及乘坐人員的感受起著重要作用[1]。駕駛員模型是真實駕駛員操縱能力的數學表達，是隨著駕駛員監控、管理、協調、補償等行為的重要性不斷增強以及控制理論的不斷發展而逐漸發展起來的新技術[2]。

駕駛員模型最初廣泛應用于車輛操縱穩定性評價，包括雙移線仿真、轉向輕便性雙移線仿真等。隨著硬件在環技術應用的發展，越來越多的車輛開發及零部件控制器硬件開發開始應用駕駛員模型進行車輛動力學及行駛仿真[3-6]，以此驗證控制器的可靠性及其他性能。智能駕駛技術的發展擴大了駕駛員模型的應用范圍，在主動安全控制系統設計領域有了新的應用[7-9]。同時，駕駛員模型也被應用于智能車控制系統開發[10-11]，可以跟隨目標軌跡和目標速度，決策出相應的轉向盤轉角和加速踏板、制動踏板開度。

硬件在環、控制器在環技術中，不同駕駛員駕駛同一輛車時，車輛響應有所不同，因此以駕駛風格細分的駕駛員模型能夠更全面地測試控制器及車輛特性。以基于最優預瞄的駕駛員縱向加速度模型為基礎，以跟隨速度為參考量，發展得到基于多點多目標的決策模型，同時基于縱向加速度及縱向加速變化率進行2階預瞄決策，并以預瞄視野、決策意愿和決策偏差表征駕駛員的駕駛風格進行建模。通過Simulink-Carsim聯合仿真，驗證模型可以反映出不同駕駛風格下的駕駛行為，豐富了駕駛員縱向加速度模型對不同駕駛風格的模擬。

1 表征預瞄視野的多點預瞄決策建模

縱向駕駛員模型的多點預瞄類似于側向駕駛員模型，由預期軌跡預瞄區間內各點的速度進行加速度決策，如圖1所示，圖中-為大地坐標系，-為車輛坐標系。

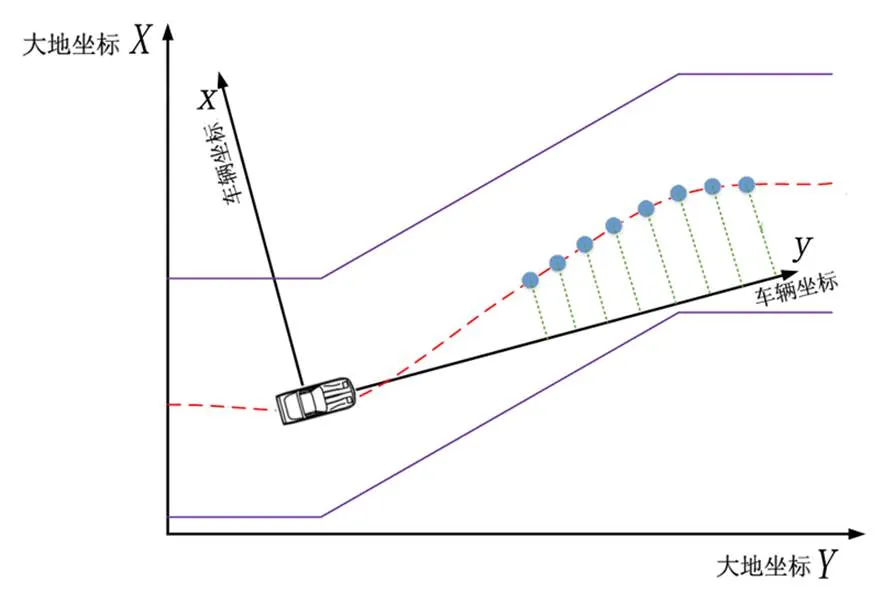
圖1 多點預瞄示意圖

在單點預瞄下，根據最優預瞄理論，車速跟隨誤差e為

e=(+)-(+) （1）

式中：為預瞄時刻；為到達預瞄點所需時間；(+)為軌跡上預瞄點處的目標車速，表示駕駛員駕駛車輛到達預瞄點處時希望的目標車速；(+)為駕駛員駕駛車輛到達預瞄點處時實際的行駛車速。根據單點預瞄最優理論得到

e=(+)-(+)=0 （2）

假設車輛在很短的距離內以勻加速運動行駛，可得

(+)=()+a×（3）

由式（2）與式（3）可得

e=(+)-()- a×=0 （4）

當駕駛員的預瞄視野中有個預瞄點時，得到

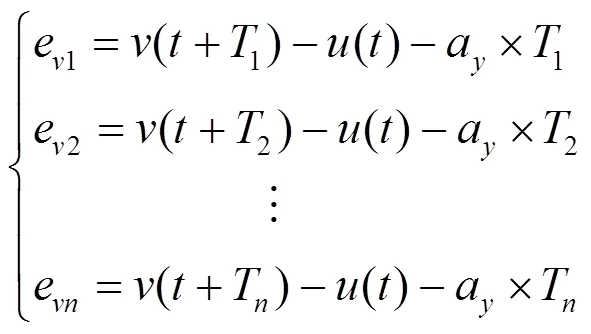
式中：（+T）為每一預瞄點處的目標車速；T為每一預瞄點對應的預瞄時間；a為縱向加速度。

合并每一點的最優預瞄目標，構建多點最優預瞄指標函數為

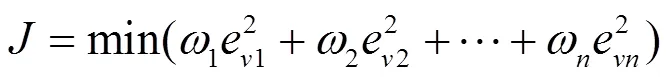
即

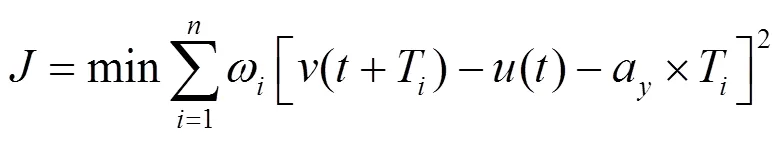
式中：ω為每一預瞄點處速度跟隨誤差的權重系數。為了體現不同預瞄點處權重的不同，定義權重系數ω（T）。駕駛員根據預瞄視野進行決策時，以近處預瞄點為主要決策依據，如圖2所示，則

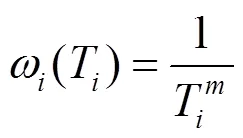
式中：為權重程度系數，值越大，權重程度越高，且相鄰兩個預瞄點之間的權重差距越大。

駕駛員根據預瞄視野進行決策時，以遠處預瞄點為主要決策依據，如圖3所示，則

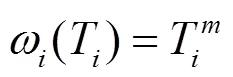
圖3 縱向預瞄窗-遠窗示意圖

駕駛員根據預瞄視野進行決策時，對每個預瞄點一視同仁，如圖4所示，則

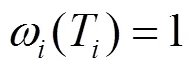
2 表征決策意愿的多目標決策建模

在智能車中，如果乘客希望以較平緩的加速度方式行駛，可以犧牲一些速度跟隨精度，這是一個跟隨精度和乘坐舒適性之間的選擇。據此，建立雙目標決策縱向模型。

目標1：最小速度跟隨誤差，強調跟隨準確性，則

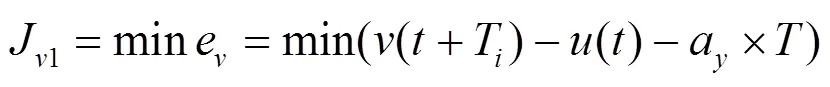
目標2：最小縱向加速度，強調乘坐舒適性，則

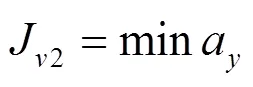
由于J1與J2兩個指標的數量級、量綱均不同，需要進行無量綱化與歸一化，得到

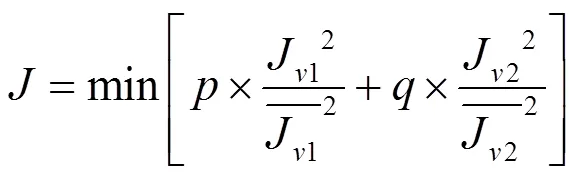
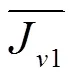
3 表征決策偏差的縱向模型

縱向加速度最優預瞄理論，即預瞄點處車速與車輛行駛速度誤差為0，進行縱向加速度決策。實際決策過程中并不能保證每次決策都得到由式（4）計算所得的準確值，而是在最優縱向加速度附近決策出接近最優值的實際縱向加速度；因此，最優縱向加速度和實際縱向加速度會產生決策偏差

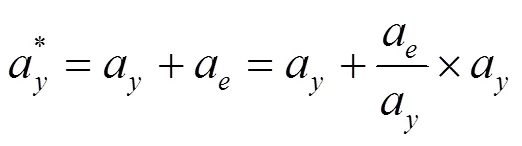
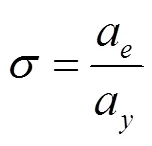
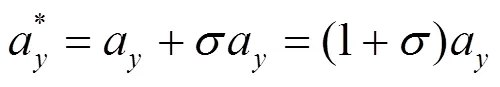
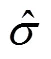
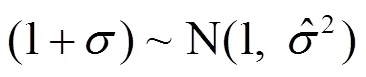
4 基于2階多點預瞄的縱向模型

在速度跟隨中，駕駛員為了駕駛車輛到達預瞄位置，決策出最優縱向加速度，車輛勻加速運動，在到達預瞄點時達到目標車速；對于某些駕駛員，決策行為不只限于縱向加速度，還包括縱向加速度變化率，以此進行車輛操控。

2階預瞄最優指標為

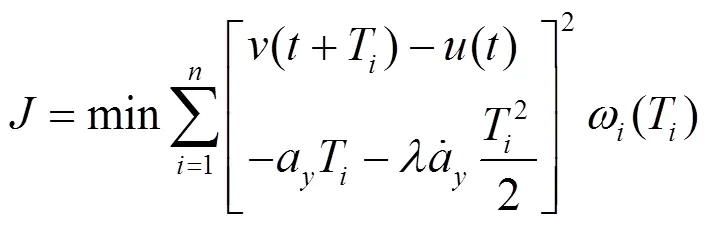
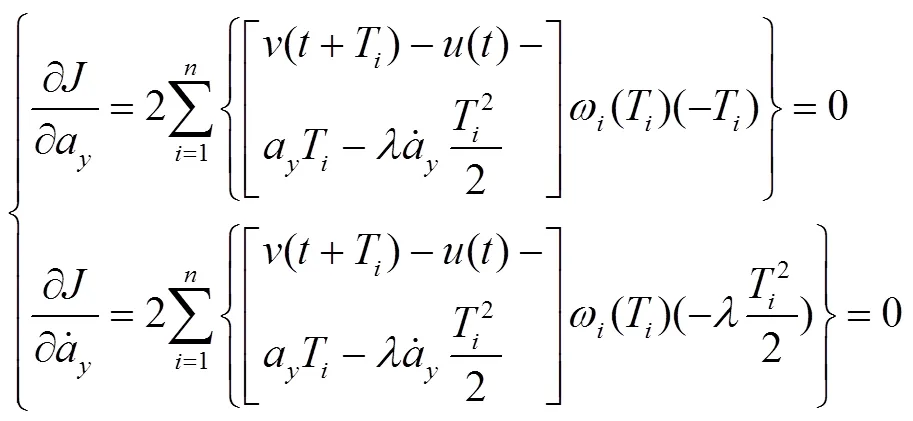
式中：為駕駛員2階預瞄的程度，為了使模型具有一般性，則0≤≤1，當=0時模型退化為1階預瞄模型。

5 仿真結果與分析

利用MATLAB軟件，通過Simulink-Carsim建立聯合仿真平臺，主要從預瞄視野、決策意愿和決策偏差、2階預瞄程度進行驗證。

（1）預瞄視野的仿真分析。

針對預瞄視野，主要從預瞄窗口權重、預瞄區間大小和預瞄點個數3個方面進行仿真。

對于預瞄窗口權重的影響，不同權重下速度跟隨曲線的對比結果如圖5所示。

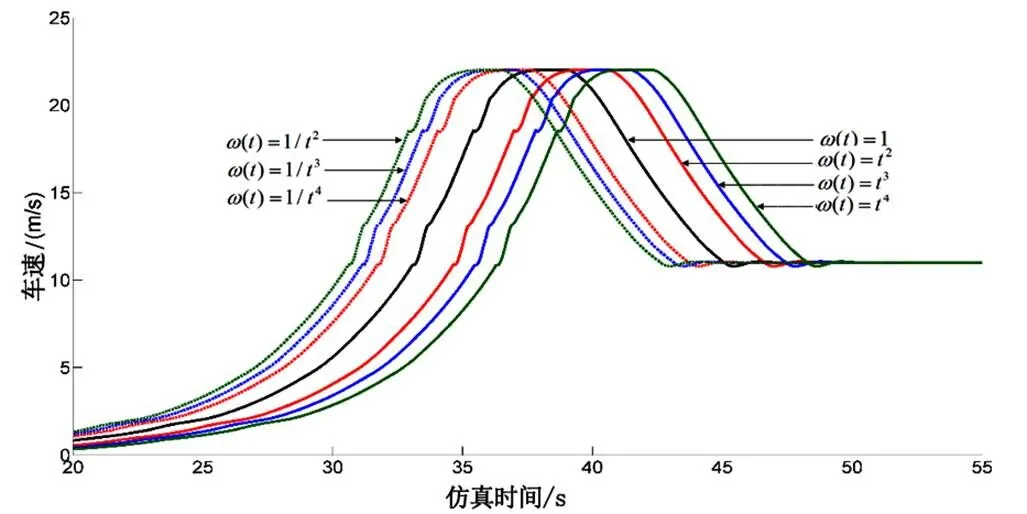
圖5 不同權重下速度跟隨曲線的對比圖

從圖5可以看出，遠處權重高的跟隨方式車輛縱向加速度較小，近處權重高的跟隨方式縱向加速度較大，并且系數越大，這種趨勢越明顯。

對于預瞄區間大小的影響，不同預瞄區間下車速跟隨與加速踏板、制動踏板輸出曲線結果如圖6所示。

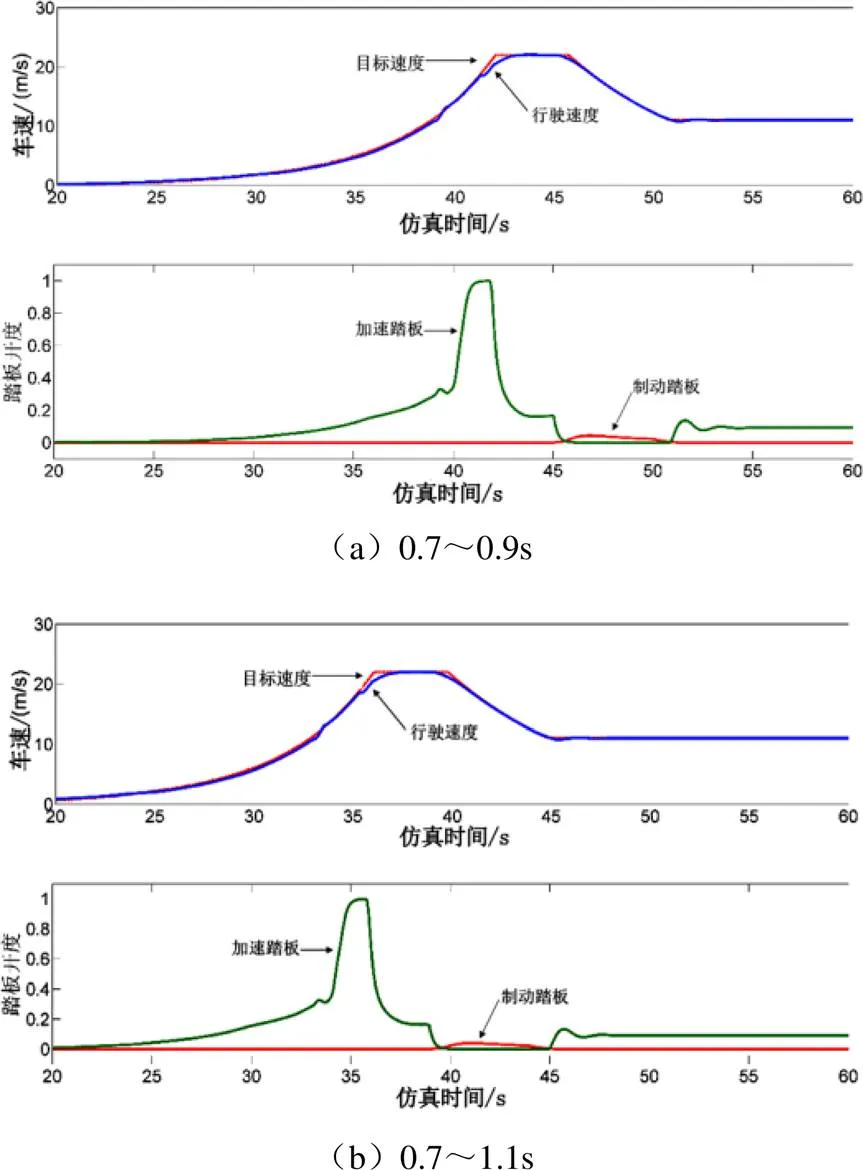
如圖6所示，預瞄區間越大，速度上升越快，縱向加速度越大。這是由于較大的預瞄區間能夠預瞄到軌跡更遠處的速度，利用遠處的速度進行決策會有更高的車速參與，使車速更快上升。

對于預瞄點個數的影響，不同預瞄點個數對車速跟隨影響的曲線如圖7所示。

從預瞄點個數的角度分析，跟隨效果無明顯變化，但在仿真過程中，仿真時間差別較大：預瞄點個數越多，仿真時間越長；反之，仿真時間越短。

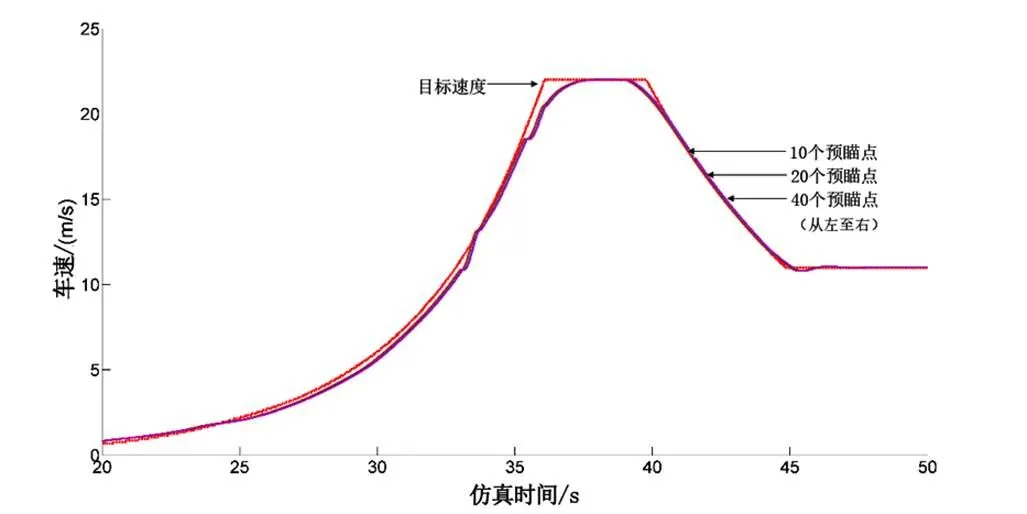
圖7 預瞄點個數對車速跟隨影響曲線圖

（2）決策意愿和偏差的仿真分析。

對于決策意愿，考查跟隨誤差權重和舒適度權重對縱向加速度決策的影響，不同決策權重對車速跟隨效果的影響結果如圖8所示。

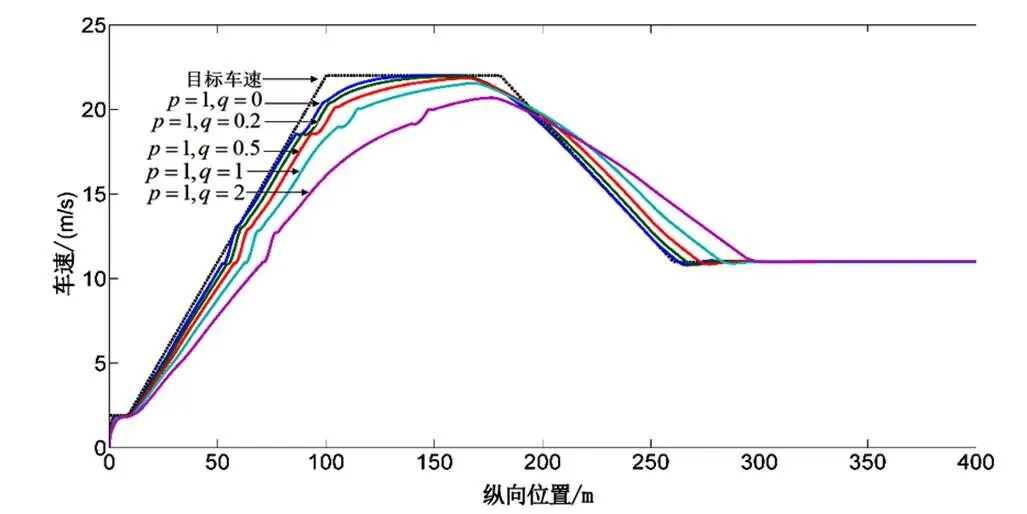
圖8 不同決策權重對車速跟隨效果影響曲線圖

如圖8所示，權重值之比/的值越大，縱向加速度越小，跟隨精度越低；/的值越小，縱向加速度越大，跟隨精度越高。具體跟隨效果及縱向加速度曲線如圖9所示。

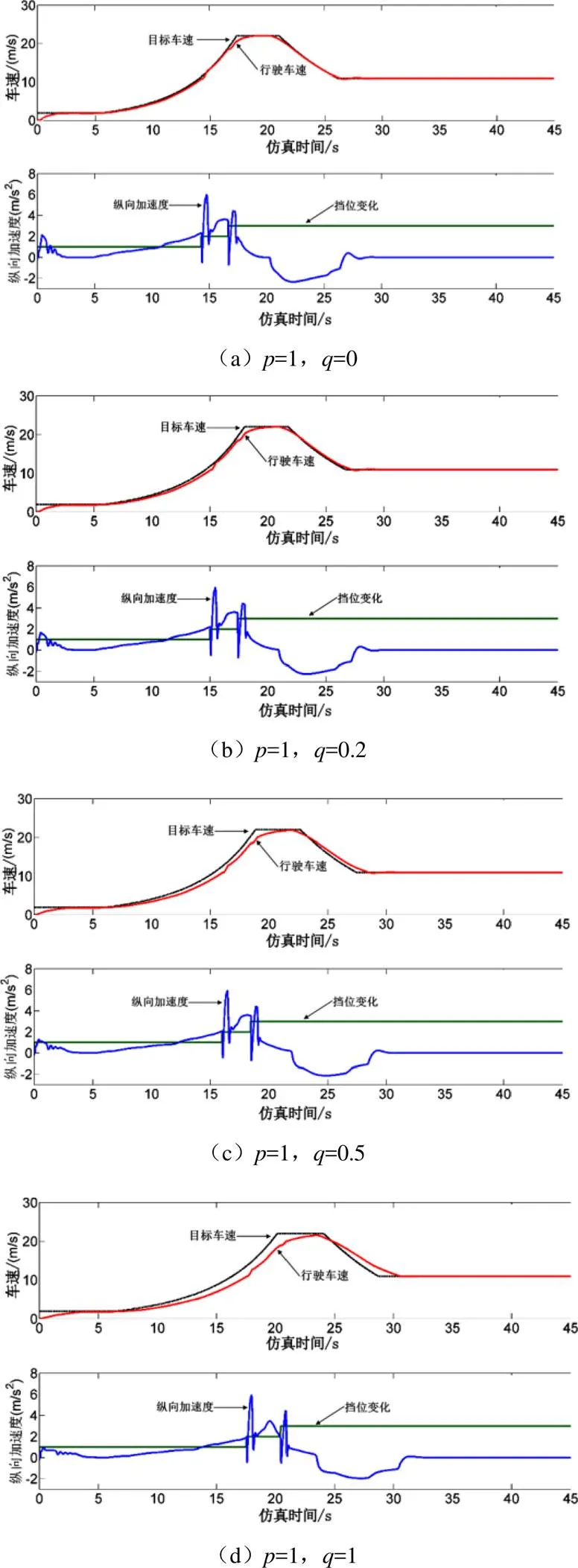
圖9 車速跟隨效果與縱向加速度曲線

從圖9可以看到，雙目標決策對縱向加速度影響明顯，提高加速度權重的比重能夠實現較好的乘坐品質。

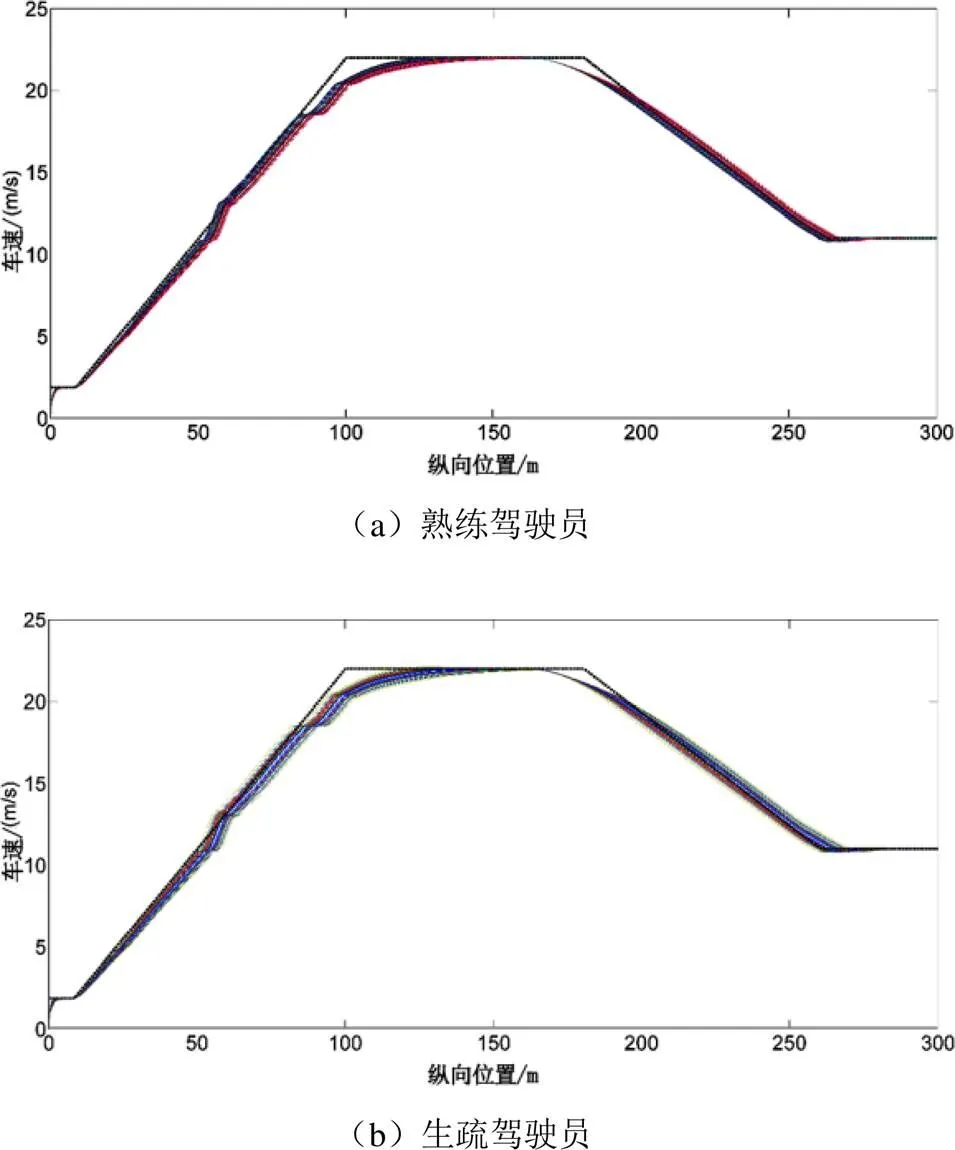
圖10 駕駛員50次仿真跟隨結果曲線

如圖10所示，熟練駕駛員的跟隨誤差總體偏小，生疏駕駛員的跟隨誤差總體偏大。

（3）2階預瞄程度的仿真分析。

針對2階預瞄程度的影響進行仿真分析，不同程度2階預瞄的車速跟隨效果曲線如圖11所示。

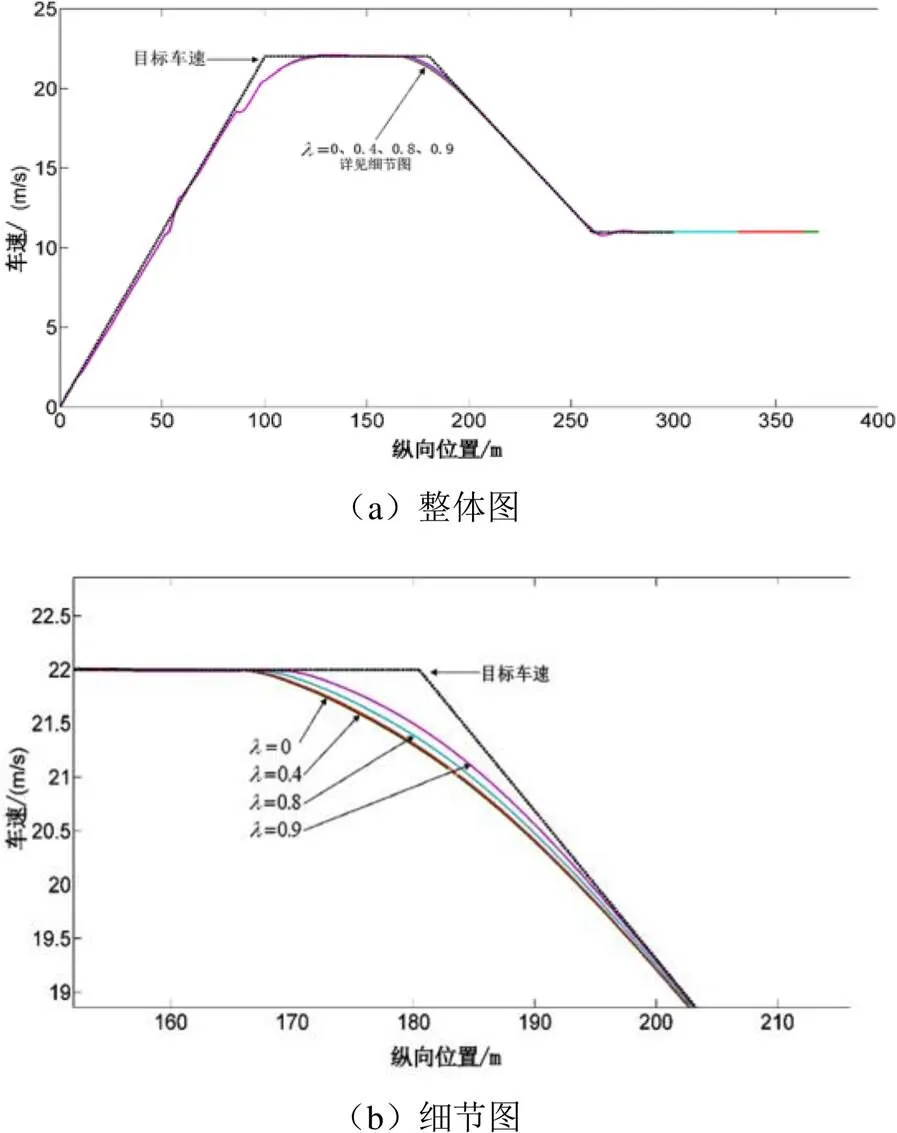
圖11 不同程度2階預瞄的車速跟隨效果曲線

如圖11所示，=0.9的2階預瞄程度速度跟隨精度有一定程度的提高。

6 總 結

改進了基于最優預瞄的駕駛員縱向加速度模型，以跟隨速度為參考量，提出多點多目標的2階預瞄決策模型，并以預瞄視野、決策意愿和決策偏差表征駕駛員的駕駛風格進行建模，通過仿真得到以下結論。

（1）多點預瞄的駕駛員模型，以預瞄窗口權重、預瞄區間大小及預瞄點個數區分駕駛員，研究3種不同參數對駕駛員操作及車輛對目標速度的跟隨效果的影響。結果顯示：預瞄窗口是對遠近重要程度的選擇，近處優先的駕駛方式下，車輛的跟隨效果更好，相對的縱向加速度也越大；預瞄區間越長，駕駛員決策行為越提前，得到的車輛操控方式越平緩，車輛的縱向加速度越小；預瞄點個數對軌跡跟隨及駕駛員操作的影響并不大，對仿真時間影響明顯，預瞄點個數越多，仿真時間越長。

（2）多目標決策駕駛員模型，在跟隨精度與縱向加速度之間進行平衡，體現不同駕駛員的駕駛意愿，表現其駕駛風格。雙目標決策算法，從最優控制的角度描述駕駛風格，具備滾動、預測、尋優的理念，控制效果平順合理。

（3）基于決策偏差精度不同的駕駛員建模方法，將原有最優預瞄決策與決策偏差精度建模相結合，區分不同能力駕駛員的決策效果。利用人類決策誤差符合正態分布的概念進行建模，在50次仿真中，決策偏差精度不同的駕駛員體現出整體上的跟隨差異。

[1]王超，郭孔輝，許男，等.表征駕駛風格和駕駛員能力的駕駛員模型[J].北京理工大學學報，2019，39（1）：41-45.

[2]王藝兵，于培人，王占林.駕駛員模型技術發展研究[J].山東紡織工學院學報，1996，9（2）：78-84.

[3]V?GEL M，VON STRYK O，BULIRSCH R，et al. An Optimal Control Approach to Real-Time Vehicle Guidance[M]. Springer Berlin Heidelberg，2003：84-102.

[4]BUTZ T，VON STRYK O. Optimal Control Based Modeling of Vehicle Driver Properties[C]//SAE World Congress & Exhibition.2005.

[5]FREZZA R，SACCON A，MINEN D. Smart Driver：A Research Project for Closed Loop Vehicle Simulation in MSC. ADAMS[J]. Multi-body Dynamics：Monitoring and Simulation Techniques III，2004：401-413.

[6]FREZZA R，SACCON A，BACCHET D. Smart Driver：A Sensor Based Model of a Car Driver for Virtual Product Development[C]// IEEE/ASME International Conference on Advanced Intelligent Mechatronics.2003（1）:366-370.

[7]GRAY A，GAO Y，HEDRICK J K，et al. Robust Predictive Control for Semi-Autonomous Vehicles with an Uncertain Driver Model[C]//Intelligent Vehicles Symposium（IV）. IEEE，2013：208-213.

[8]CHEN L K，ULSOY A G. Identification of a Driver Steering Model，and Model Uncertainty，from Driving Simulator Data[J]. Journal of Dynamic Systems Measurement and Control，2001，123（4）：623-629.

[9]ZAFEIROPOULOS S，TSIOTRAS P. Design of a Lane-Tracking Driver Steering Assist System and Its Interaction with a Two-Point Visual Driver Model[C]// 2014 American Control Conference（ACC）. IEEE，2014：3911-3917.

[10]LENAIN R，THUILOT B，CARIOU C，et al. High Accuracy Path Tracking for Vehicles in Presence of Sliding：Application to Farm Vehicle Automatic Guidance for Agricultural Tasks[J]. Autonomous Robots，2006，21（1）：79-97.

[11]LENAIN R，THUILOT B，CARIOU C，et al. Model Predictive Control for Vehicle Guidance in Presence of Sliding：Application to Farm Vehicles Path Tracking[C]// 2005 IEEE International Conference on Robotics and Automation. IEEE，2005：885-890.

2021-04-15

U462:TP391.9

A

10.14175/j.issn.1002-4581.2021.04.001

1002-4581（2021）04-0001-06