網型防爆墻防護效果數值模擬

張曉聰

(廣州大學 土木工程學院, 廣東 廣州 510006)

防爆墻通常設置在目標建筑物的周圍，用來為其后方區域的建筑物、人員提供一定的安全防護.作為一種被動防護措施，防爆墻從兩方面來減弱作用在建筑物上的爆炸荷載：①防爆墻可以阻擋恐怖分子接近目標建筑物，從而提供了一定的防護距離；②防爆墻通過改變爆炸波的傳播路徑，使爆炸波的能量得到分散，從而降低了目標建筑物上的爆炸波能量輸入[1-2].此外，由于建造相對容易，防爆墻在軍用和民用領域均得到了大規模應用.因此，不斷改進防爆墻的設計，使其達到安全性、經濟性以及美觀性的統一，就顯得十分必要.

世界各國的學者和工程技術人員開發了各種形式的防爆墻，這些防爆墻按原理可分為實體防爆墻、犧牲層結構以及新型防爆墻3類.其中，實體防爆墻[3]利用其結構的剛性將一部分爆炸波的能量反射回去，犧牲層結構[4-5]利用其柔性來吸收爆炸波能量，而新型防爆墻[6-11]則利用爆炸波本身的傳播特性以及結構與爆炸波的復雜相互作用(不局限于爆炸波的反射和能量吸收)，比如通過不同爆炸波之間的相互作用來實現波能自消耗.

Zong等[8]基于波能自消耗的概念，提出了由一排護欄柱構成的護欄型防爆墻設計，通過相鄰護欄柱繞射波之間的相互作用，在墻后區域發生爆炸波能量的自消耗，從而為墻后人員和建筑物提供防護.通過開展二維的數值模擬，證明了護欄型防爆墻在減小墻后爆炸荷載的有效性.

侯帥波[10]提出了在護欄柱前方增加橫桿的網型防爆墻設計，并通過數值模擬證明了網型防爆墻的防護有效性和安全性，但是未對網型防爆墻的衰減機理作深入分析.此外，該研究中橫桿和縱桿的直徑取值為100 mm，這與網型防爆墻在實際應用時有較大差距.因此，本研究中的橫桿、縱桿全部采用圓形截面，并以20 mm為基本直徑尺寸，以最大程度接近實際應用場景.

本文比較了網型防爆墻與護欄型防爆墻在同一工況下的爆炸荷載衰減率，從而對網型防爆墻的防護效果作出評價，并對其防護原理進行了分析.

1 數值模型的建立

1.1 計算方法介紹

在數值模擬中，通過對比墻后各個測點的超壓峰值與沖量，來研究墻后區域爆炸荷載的分布，從而對防爆墻的防護有效性作出評估.典型的測點超壓時程曲線如圖1所示.

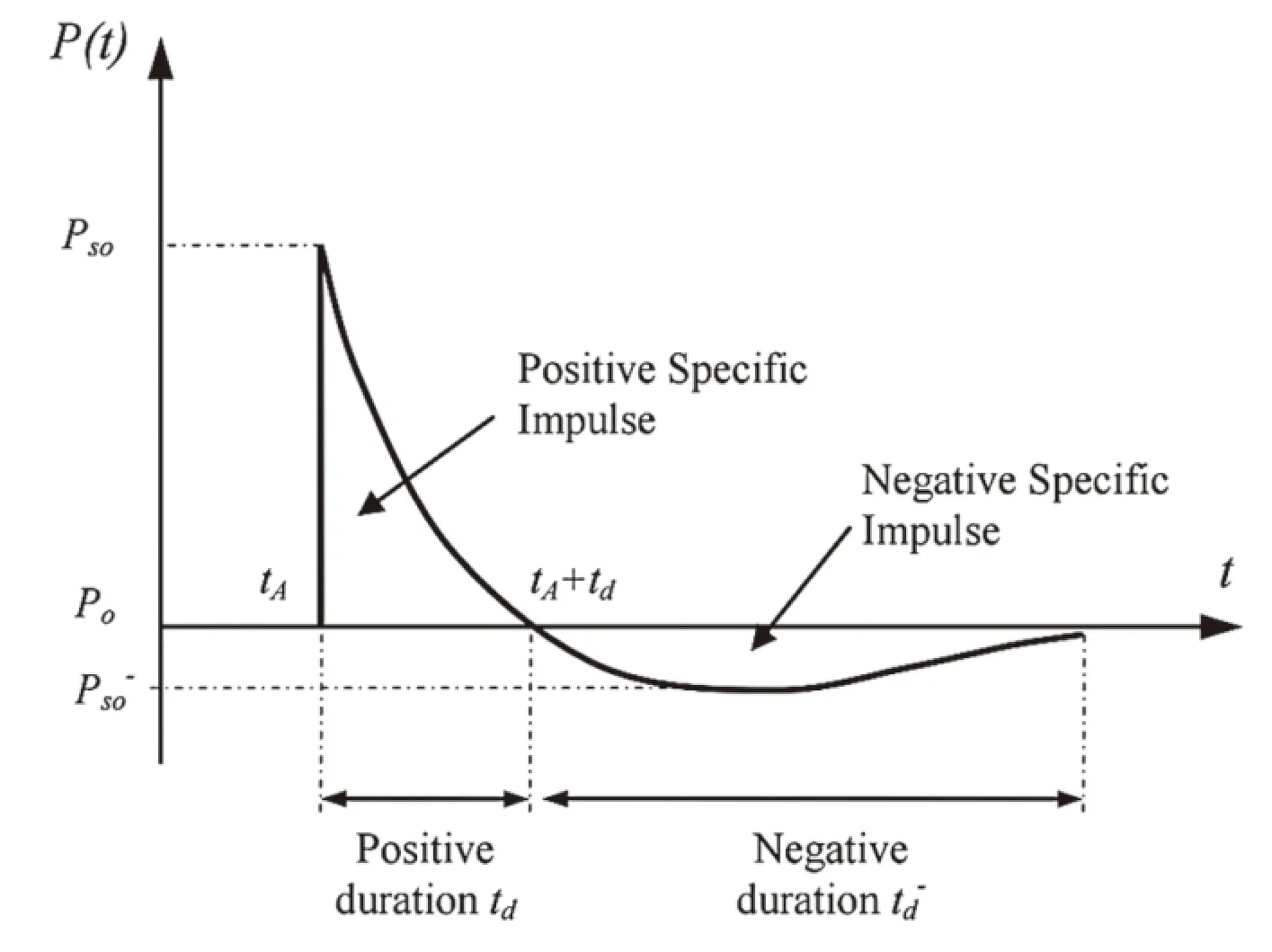
圖1 典型的測點超壓時程曲線[12]Fig.1 Typical blast pressure profile of gauges

采用LS-DYNA軟件的LBE/ALE方法進行數值模擬，其計算過程分為兩個階段：①利用Kingery[13]的經驗公式，計算出空氣域前表面的爆炸超壓分布；②以前一階段的計算結果為初始條件，利用ALE單元模型的多物質選項，對爆炸波在空氣中的傳播、結構與爆炸波的相互作用進行模擬.因此，LBE/ALE方法只需要對結構周圍一定范圍內的空氣進行建模，從而使計算量明顯減小.在LBE/ALE模型中，空氣域模型的前表面被定義為周圍層(Ambient layer)，從而可以接收經驗公式法計算得到的爆炸超壓分布.

利用流固耦合算法(關鍵字*CONSTRAINED_LAGRANGE_IN_SOLID)，可以對結構與爆炸波的相互作用進行建模，從而模擬爆炸波的反射、繞射、透射以及能量吸收現象.流固耦合算法利用ALE空氣單元計算出結構所受的作用力，與此同時，結構為爆炸波的傳播提供了約束條件.

1.2 模型參數的確定

圖2為計算模型示意圖.取1.0 kg TNT炸藥地面起爆的工況進行分析.空氣域的長度、寬度和高度分別為3.1 m、4.0 m和2.0 m.由于模型的對稱性，只需建立1/2寬度，即2.0 m寬的空氣域模型即可.防爆墻的寬度為4.0 m，高度為1.0 m，與炸藥中心的距離均為1.25 m.在防爆墻后方0.25 m、0.75 m、1.25 m、1.75 m及2.25 m分別布置了5個測點，測點高度均為0.25 m.為便于描述測點的位置，引入無量綱量D/H，其中，D為測點的墻后距離，H為防爆墻的高度，5個測點對應D/H分別為0.25、0.75、1.25、1.75和2.25，并用T1-T5代表防爆墻后的5個測點.模型的下表面設為固定邊界，以模擬地面對爆炸波的反射現象；由模型的對稱性，右表面應設為對稱邊界；上表面、后表面、左表面均設為無反射邊界，以達到模擬無限大空氣域的效果.由于結構的剛度對爆炸荷載的計算結果影響不大[14]，因此，將防爆墻視為剛體，從而簡化計算.

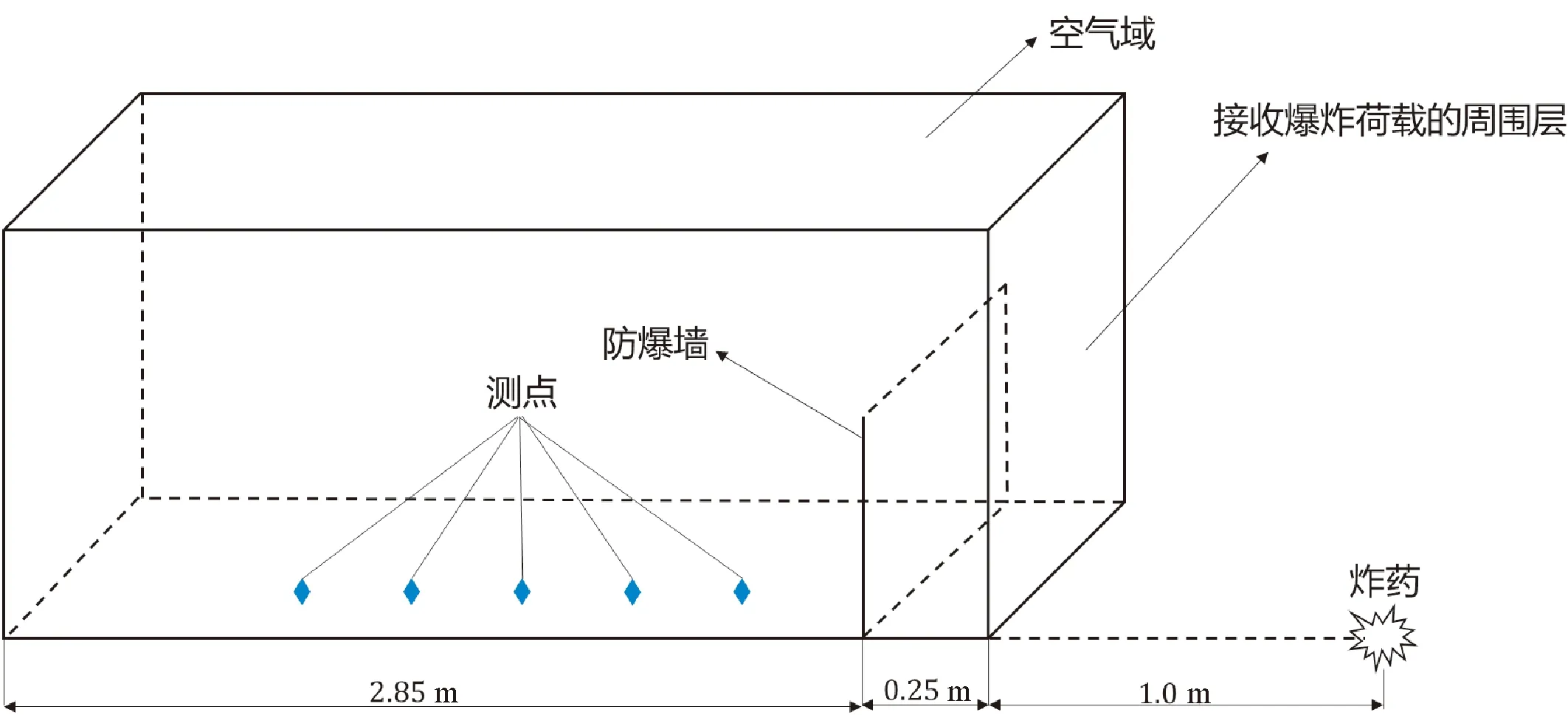
圖2 計算模型示意圖Fig.2 Sketch of numerical model

在本文的模型中，防爆墻的寬度為4.0 m，高度為1.0 m，與炸藥中心的距離均為1.25 m.綜合考慮護欄的防護效果與自身所承受的凈爆炸荷載[8, 15]，以及在城市地區應用的實際情況，將護欄的截面形狀確定為圓形.

空氣采用理想氣體模型，其材料模型通過關鍵字*MAT_NULL定義，狀態方程通過關鍵字*EOS_LINEAR_POLYNOMIAL定義，空氣單元的壓強表達式如(1)所示：

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)e

(1)

式中，μ=ρ/ρ0-1，其中,ρ和ρ0分別為空氣在當前時刻和初始時刻的密度；e為單位體積空氣的內能；常數C0=C1=C2=C3=C6=0，C4=C5=γ-1，其中，絕熱指數γ=1.4.將空氣單元的初始壓強設為101.325 kPa，密度設為1.225 kg/m3，以模擬平均海平面的海拔高度以及15 ℃溫度條件的標準工況.

1.3 網格收斂性測試

為確定合理的網格尺寸，比較了3種不同的空氣網格尺寸，即60 mm、30 mm以及15 mm在自由空氣場的工況下的計算結果，見圖3.取1.0 kg TNT炸藥地面起爆的工況進行分析.空氣域的長度、寬度、高度分別為3.1 m、4.0 m和2.0 m.由于模型的對稱性，只需建立1/2寬度，即2.0 m寬的空氣域模型即可.在距離炸藥中心1.5 m、2.0 m、2.5 m、3.0 m及3.5 m處布置了5個測點，且測點高度均為0.25 m.模型的下表面設為固定邊界，以模擬地面對爆炸波的反射現象；由模型的對稱性，右表面應設為對稱邊界；上表面、后表面和左表面均設為無反射邊界，以達到模擬無限大空氣域的效果.從圖 3可以看出，空氣網格尺寸的變化對沖量值的影響不明顯，沖量在30 mm網格時就已收斂.而超壓峰值對網格尺寸的變化較為敏感.由于計算機的性能有限，選取15 mm為空氣網格尺寸.

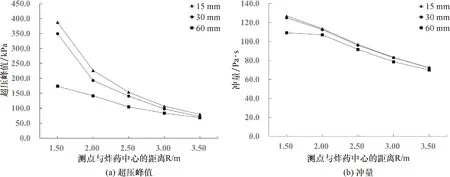
圖3 網格收斂性測試結果Fig.3 Mesh convergence test results

1.4 模型驗證

通過單層圓形護欄柱的現場試驗結果[7]，來驗證數值模型的正確性.按照該試驗的布置方案(圖4)，取1.0 kg TNT炸藥地面起爆的工況進行分析，空氣域的長度、寬度、高度分別為3.1 m、6.0 m和2.0 m.由于模型的對稱性，只需建立1/2寬度，即3.0 m寬的空氣域模型即可.防爆墻的寬度為6.0 m，高度為1.0 m，與炸藥中心的距離為1.25 m.所有護欄柱的直徑均為20 mm，柱間凈距為10 mm.模型的下表面設為固定邊界，以模擬地面對爆炸波的反射現象；由模型的對稱性，右表面應設為對稱邊界；上表面、后表面、左表面均設為無反射邊界，以達到模擬無限大空氣域的效果.由于結構的剛度對爆炸荷載的計算結果影響不大[14]，因此將防爆墻視為剛體，從而簡化計算.分別選取墻后距離為0.8 m、1.8 m和2.8 m的3個測點，測點的超壓峰值與沖量的對比結果如圖 5所示.從圖5可以看出，測點的沖量結果與試驗結果吻合較好，超壓峰值雖與試驗結果相比偏低，但3個測點的誤差均在11.5%以下，從而證明了模型在預測墻后爆炸荷載方面的準確性.

圖4 單層圓形護欄柱的現場試驗[7]

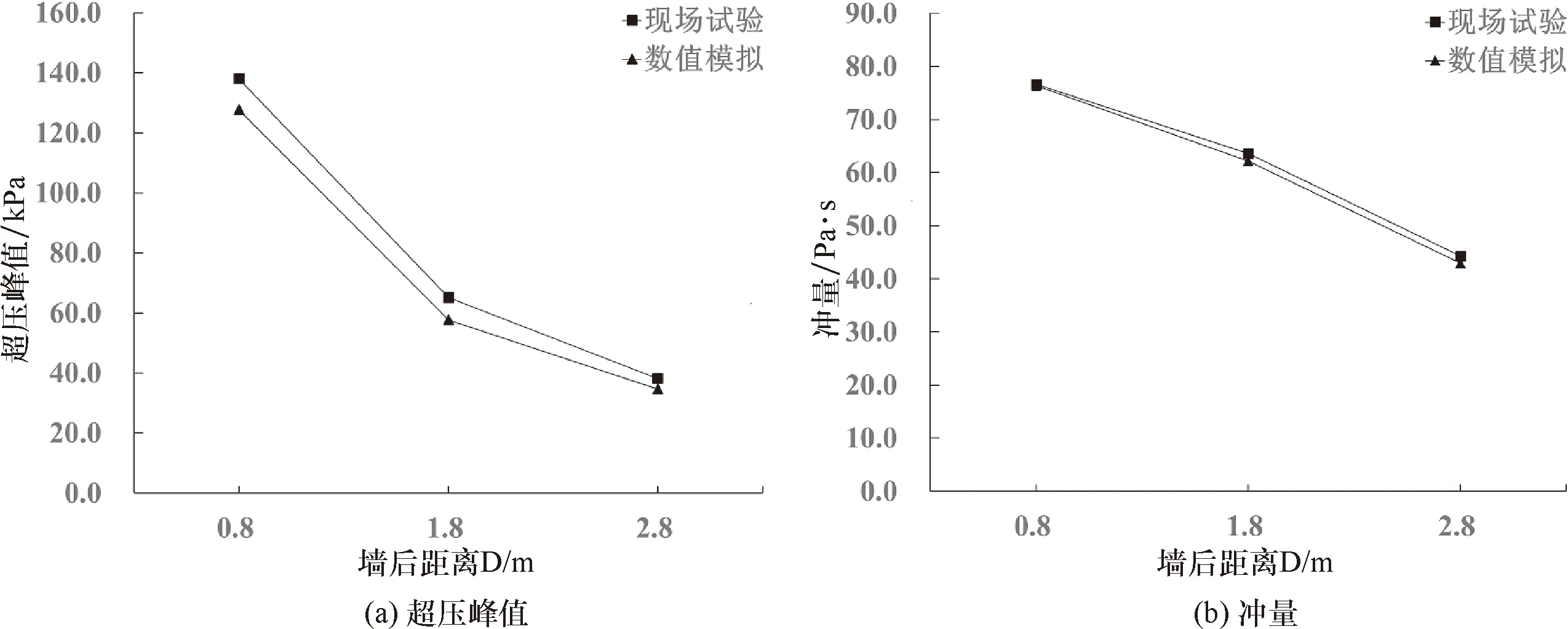
圖5 模型驗證結果Fig.5 Model validation results

2 計算結果

在1.0 kg TNT炸藥地面起爆的工況下，比較了網型防爆墻與護欄型防爆墻對墻后爆炸荷載的衰減比例，從而對網型防爆墻的防護效果做出評價，同時對其防護原理進行分析.空氣域的長度、寬度、高度分別為3.1 m、4.0 m和2.0 m.由于模型的對稱性，只需建立1/2寬度，即2.0 m寬的空氣域模型即可.防爆墻的寬度為4.0 m，高度為1.0 m，與炸藥中心的距離均為1.25 m.在防爆墻后方0.25 m、0.75 m、1.25 m、1.75 m及2.25 m分別布置了5個測點，測點高度均為0.25 m.為了便于描述測點的位置，引入無量綱量D/H，其中，D為測點的墻后距離，H為防爆墻的高度，5個測點分別對應D/H為0.25、0.75、1.25、1.75、2.25，并用T1-T5代表防爆墻后的5個測點.模型的下表面設為固定邊界，以模擬地面對爆炸波的反射現象；由模型的對稱性，右表面應設為對稱邊界；上表面、后表面、左表面均設為無反射邊界，以達到模擬無限大空氣域的效果.其中，護欄型防爆墻的縱桿直徑為20 mm，桿間凈距為10 mm(相對空隙率ROF=33%).對護欄型防爆墻和網型防爆墻而言，由于相對空隙率對其防護效果起著決定性作用[16]，同時考慮實際施工的簡便，將網型防爆墻的橫、縱桿間距比設為1.為保證對比的公平性，網型防爆墻的用鋼量、相對空隙率均與護欄型防爆墻保持一致，經過計算確定其縱桿與橫桿的直徑均為15.8 mm，縱桿間距與橫桿間距均為21.6 mm，如圖6所示.

圖6 護欄型防爆墻與網型防爆墻的模型示意圖Fig.6 Configuration of fence blast wall and net blast wall

2.1 網型防爆墻與護欄型防爆墻的防護效果對比

圖7和圖8分別給出了網型防爆墻與護欄型防爆墻的墻后爆炸荷載對比結果.從圖7、8可以看出：①與自由空氣場工況相比，網型防爆墻與護欄型防爆墻對其后方區域的爆炸荷載均有一定程度的削弱；②網型防爆墻對墻后測點超壓峰值的衰減效果優于護欄型防爆墻，但是這一優勢隨著D/H的增大而逐漸減弱；③整體而言，網型防爆墻對墻后測點沖量值的衰減效果不如護欄型防爆墻.當D/H=0.25時，網型防爆墻后方測點的沖量低于護欄型防爆墻；當D/H=0.75時，網型防爆墻后方測點的沖量與護欄型防爆墻相差不大；當D/H≥1.25時，網型防爆墻后方測點的沖量反而高于護欄型防爆墻.

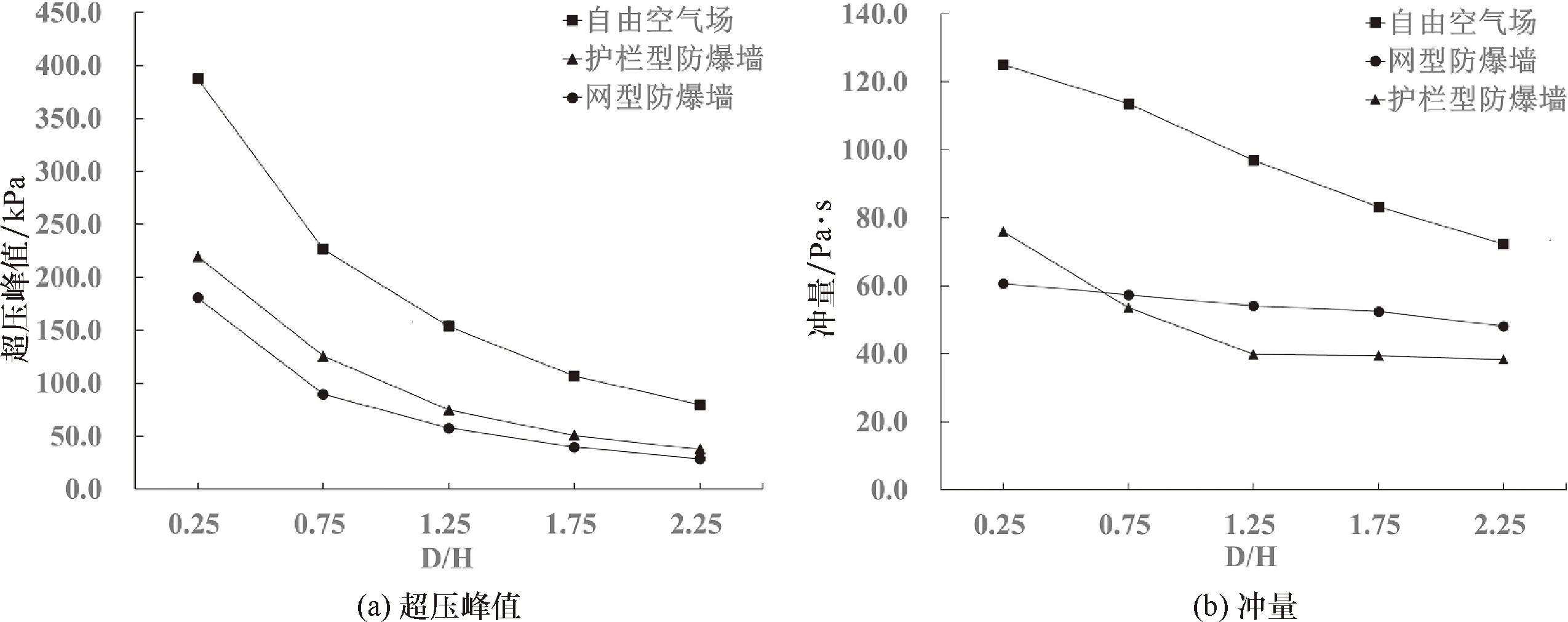
圖7 網型防爆墻與護欄型防爆墻的墻后爆炸荷載對比結果Fig.7 Comparison of peak reflected overpressure and impulse on fence blast wall and net blast wall

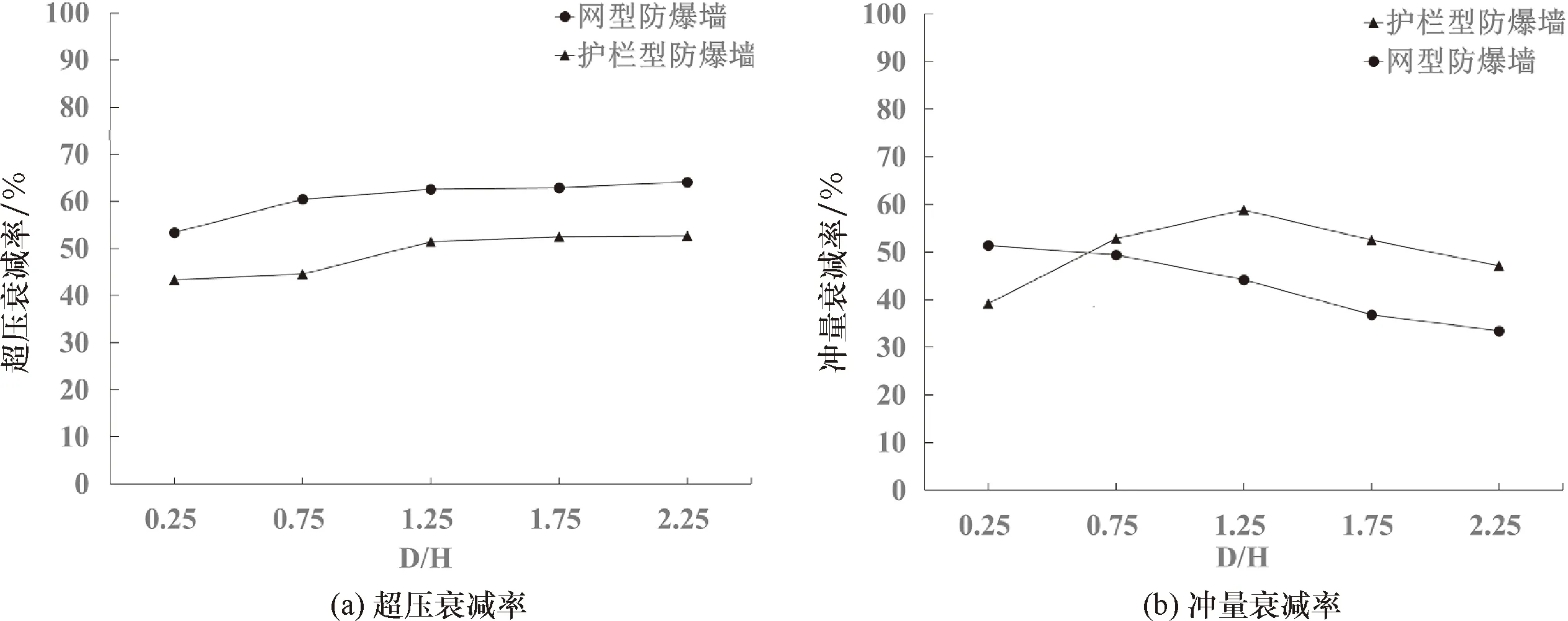
圖8 網型防爆墻與護欄型防爆墻的墻后爆炸荷載衰減率對比結果Fig.8 Comparison of blast load reduction on fence blast wall and net blast wall

2.2 超壓時程曲線分析

圖9給出了護欄型防爆墻在測點T1、T2處的超壓時程曲線.從圖9可以看出，護欄型防爆墻在墻后測點T1和T2處的超壓時程曲線接近于單峰.這說明，護欄型防爆墻在這兩個測點處的超壓主要由透射波組成，即陰影效應占主導.

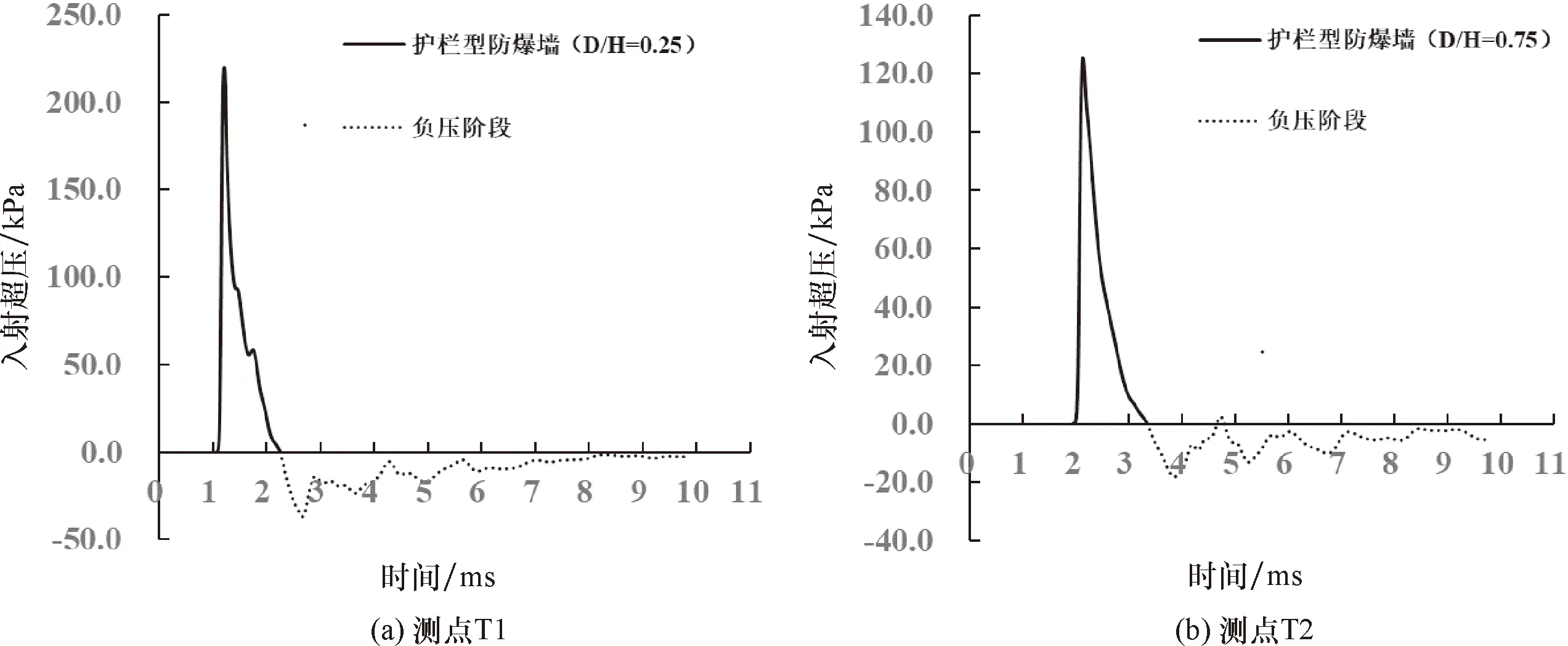
圖9 護欄型防爆墻在測點T1、T2處的超壓時程曲線Fig.9 Overpressure-time histories at T1-T2 of fence blast wall

圖10給出了護欄型防爆墻在測點T3、T4及T5處的超壓時程曲線.從圖10可以看出，雖然護欄型防爆墻在測點T3、T4和T5處的超壓時程曲線出現了雙峰或多峰現象，但是對這些測點的爆炸荷載影響不大.這是因為：①測點的第二個超壓峰值明顯低于第一個超壓峰值，因此對測點的超壓峰值沒有影響；②測點第二次出現正相超壓是在測點經歷了一段負壓之后，加上該正壓的峰值較小，因此對沖量的影響不明顯.

圖10 護欄型防爆墻在測點T3、T4、T5處的超壓時程曲線Fig.10 Overpressure-time histories at T3-T5 of fence blast wall

圖11給出了網型防爆墻在墻后測點T1處的超壓時程曲線.從圖11可以看出，網型防爆墻在測點T1處已有一定的疊加效應.但是，由于測點第二次出現的正相超壓峰值較小，因此對測點的超壓峰值沒有影響，且對測點沖量值的影響較為有限.換言之，網型防爆墻在測點T1處的爆炸荷載仍主要由透射波所決定，即測點T1仍屬于由陰影效應占主導的陰影區域.

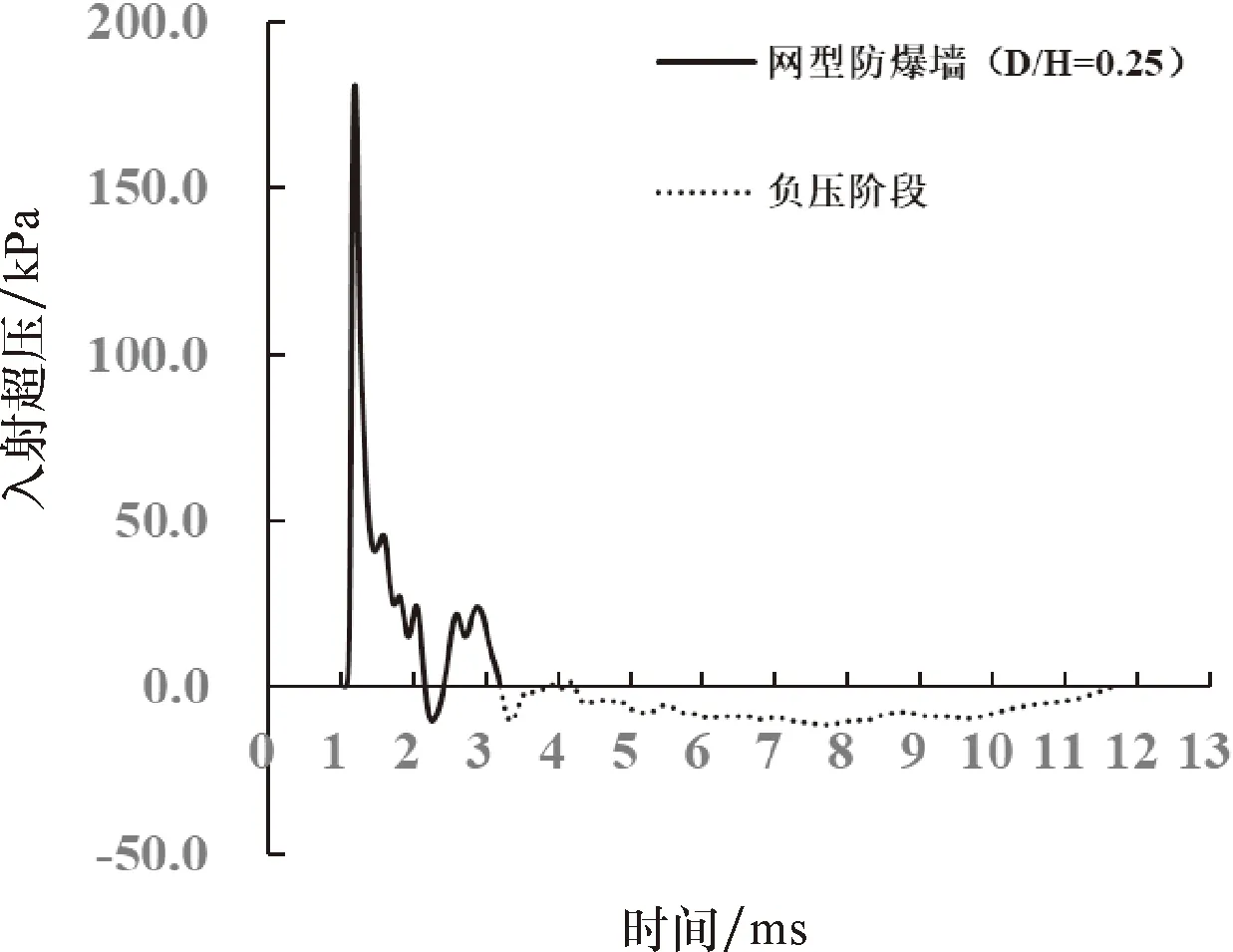
圖11 網型防爆墻在墻后測點T1處的超壓時程曲線Fig.11 Overpressure-time histories at T1 of net blast wall

圖12給出了網型防爆墻在墻后測點T2、T3、T4和T5處的超壓時程曲線.從圖12可以看出，網型防爆墻在測點這幾處的疊加效應較為顯著，且隨著D/H的增大，在第一個超壓峰值之后出現的正相超壓對測點的爆炸荷載影響較為明顯.這說明，隨著D/H的增大，陰影效應對網型防爆墻后方測點爆炸荷載的影響逐漸減弱，而疊加效應逐漸增強，并占據主導地位.

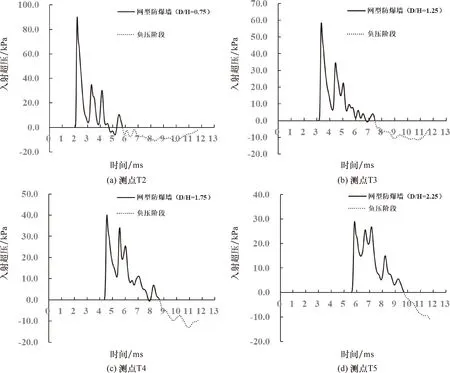
圖12 網型防爆墻在墻后測點T2、T3、T4、T5處的超壓時程曲線Fig.12 Overpressure-time histories at T2-T5 of net blast wall

2.3 超壓峰值分析

圖13和圖14分別給出了護欄型防爆墻和網型防爆墻各測點取得超壓峰值時的壓強云圖.從圖13、14可以看出，無論是護欄型防爆墻，還是網型防爆墻，其墻后測點的超壓第一次達到峰值(也是測點最終的超壓峰值)的時刻都恰好是透射波到達相應測點的時刻.這說明，對于護欄型防爆墻與網型防爆墻來說，墻后測點的超壓峰值僅取決于透射波，而由于透射波的強度主要取決于陰影效應，因此，墻后測點的超壓峰值主要由陰影效應的顯著程度決定.

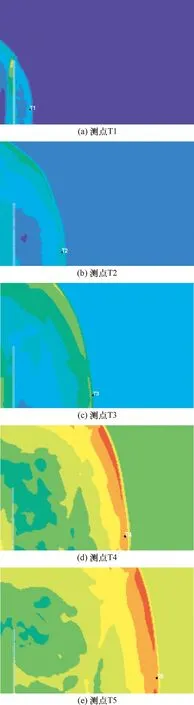
圖13 護欄型防爆墻各測點達到超壓峰值時的壓強云圖Fig.13 Pressure contour of gauges behind the fence blast wall

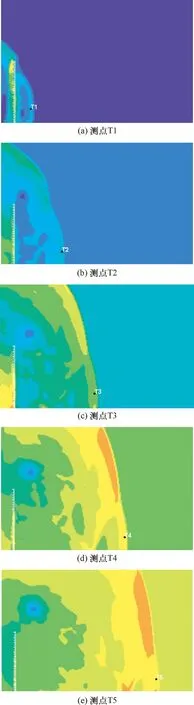
圖14 網型防爆墻各測點達到超壓峰值時的壓強云圖Fig.14 Pressure contour of gauges behind the net blast wall

雖然網型防爆墻與護欄型防爆墻的用鋼量、相對空隙率均保持一致，但是從二者墻后測點的超壓峰值結果(圖7)可以看出，網型防爆墻的陰影效應比護欄型防爆墻更加顯著.這可能是由于雖然二者對爆炸波的反射面積相等，但由于地面起爆的工況使得防爆墻前表面的爆炸荷載并不是均勻分布的，而是越靠近地面的爆炸荷載越大，從而導致對于這兩種防爆墻而言，反射表面越靠近地面，其對爆炸波的反射作用越顯著.

通過觀察網型防爆墻與護欄型防爆墻的反射面積分布(圖6)可以看出，雖然反射表面的總面積相等，但由于網型防爆墻靠近地面的反射面積所占比例更大，因此，即使在用鋼量、相對空隙率均保持一致的情況下，網型防爆墻對爆炸波的反射效果依然優于護欄型防爆墻，即網型防爆墻后方的陰影效應比護欄型防爆墻更加顯著，從而導致網型防爆墻在所有測點處的超壓峰值均低于護欄型防爆墻.

2.4 沖量分析

圖15給出了網型防爆墻與護欄型防爆墻在測點T1處的超壓時程曲線對比結果.從圖15可以看出，與護欄型防爆墻相比，雖然網型防爆墻測點的超壓持續時間更長，但由于網型防爆墻測點的超壓峰值更低，而且隨后出現的正相超壓對測點的總沖量值影響有限，從而導致網型防爆墻在測點T1處的沖量值低于護欄型防爆墻.

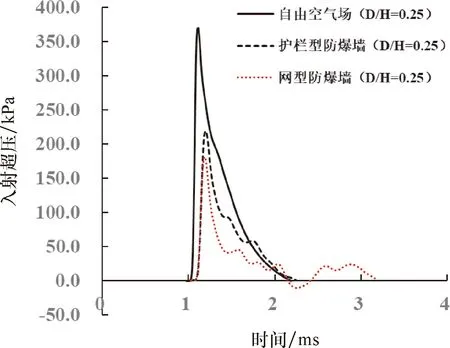
圖15 網型防爆墻與護欄型防爆墻在測點T1處的超壓時程曲線對比結果

圖16給出了網型防爆墻與護欄型防爆墻在測點T2處的超壓時程曲線對比結果.從圖16可以看出：①與護欄型防爆墻相比，網型防爆墻在測點T2處的正壓持續時間更長；②網型防爆墻后方測點T2的超壓峰值低于護欄型防爆墻.這兩方面因素共同作用，使得兩種防爆墻在測點T2處的沖量結果相差不大.

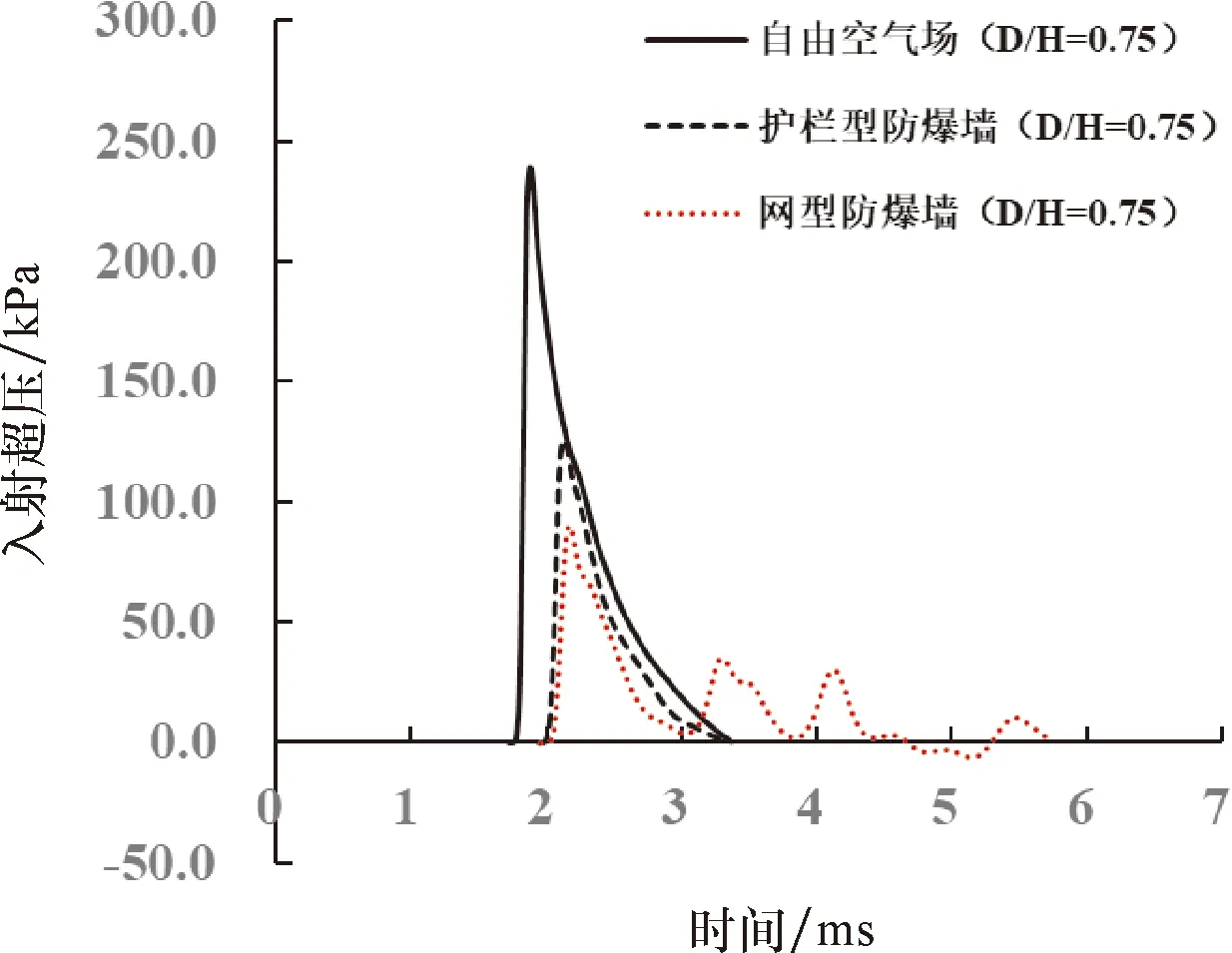
圖16 網型防爆墻與護欄型防爆墻在測點T2處的超壓時程曲線對比結果

圖17給出了網型防爆墻與護欄型防爆墻在測點T3、T4、T5處的超壓時程曲線對比結果.從圖17可以看出，對網型防爆墻而言，當D/H≥1.25時，由于隨后出現的多個超壓峰值與第一個超壓峰值越來越接近，其對測點沖量值的影響較為顯著，從而導致網型防爆墻的疊加效應越來越明顯；而護欄型防爆墻在D/H≥1.25的測點處超壓時程曲線接近于單峰，仍由陰影效應占主導，而疊加效應不明顯.因此，當D/H≥1.25時，網型防爆墻的沖量值反而大于護欄型防爆墻.

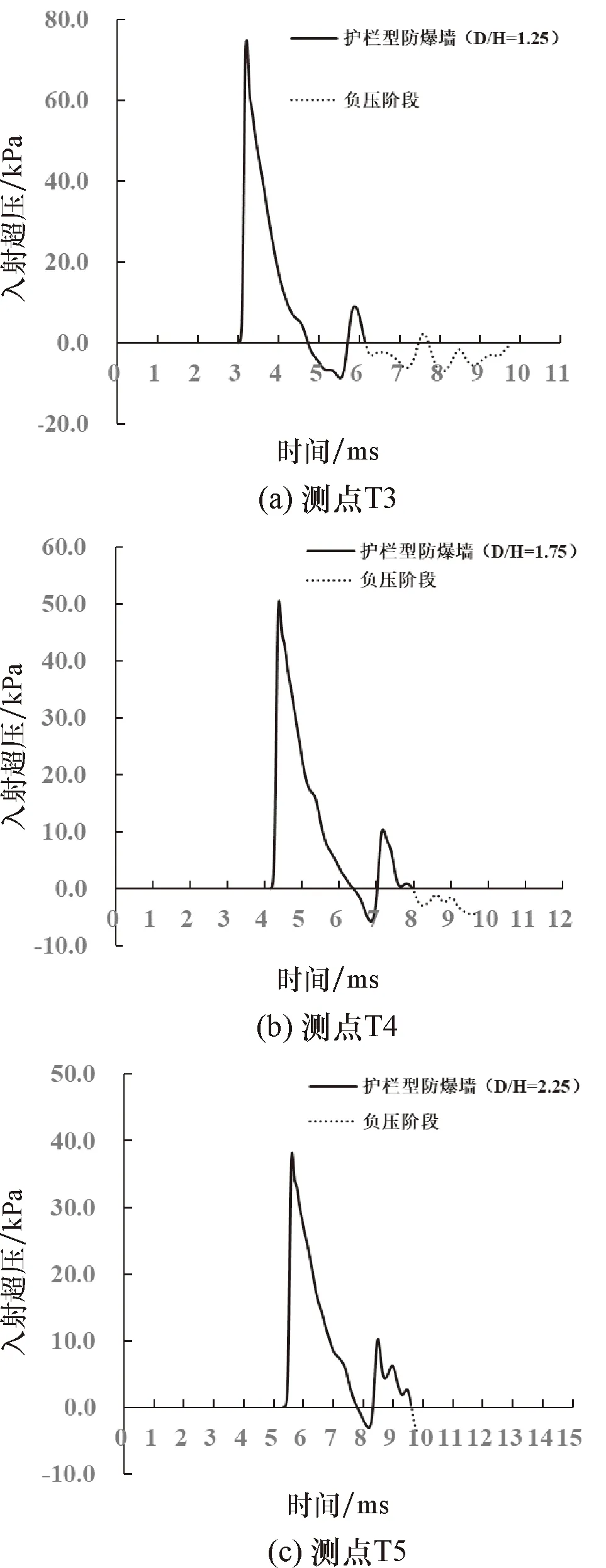
圖17 網型防爆墻與護欄型防爆墻在測點T3、T4、T5處的超壓時程曲線對比結果

3 結 論

本文通過數值模擬研究，對比了網型防爆墻與護欄型防爆墻在1.0 kg TNT炸藥地面起爆、防爆墻與炸藥中心距離為1.25 m工況下的墻后爆炸荷載.結果表明，網型防爆墻在超壓峰值方面的衰減效果優于護欄型防爆墻，但在沖量方面整體不如護欄型防爆墻，這是由于網型防爆墻后方區域的疊加效應較為顯著.因此，在實際應用中，當目標建筑物的墻后距離在0.75倍的墻高范圍內時，宜采用網型防爆墻；當目標建筑物與防爆墻的距離超出0.75倍的墻高范圍后，應采用護欄型防爆墻.