正確畫圖直觀解題

摘 要：在初中數(shù)學(xué)課堂上，畫圖屬于非常有效的解題策略之一，畫圖能夠?qū)㈩}目中一些較為復(fù)雜的數(shù)量關(guān)系直接提取出來，由此化繁為簡(jiǎn)，便于學(xué)生迅速理清解題思路.因此在初中數(shù)學(xué)教學(xué)中，教師應(yīng)當(dāng)恰當(dāng)進(jìn)行畫圖訓(xùn)練，深入淺出的挖掘教材中的圖形資源，使學(xué)生能夠快速且準(zhǔn)確的作圖，通過畫圖來解決數(shù)學(xué)問題，全面提高學(xué)生的綜合能力.

關(guān)鍵詞：初中數(shù)學(xué);畫圖解題;教學(xué)策略

中圖分類號(hào)：G632文獻(xiàn)標(biāo)識(shí)碼：A文章編號(hào)：1008-0333（2021）11-0004-02

作者簡(jiǎn)介：王莉璠（1982.12-），江蘇省無錫人，中學(xué)一級(jí)教師，從事初中數(shù)學(xué)教學(xué)研究.

在初中數(shù)學(xué)教學(xué)中，大部分內(nèi)容都與圖形有關(guān)，如函數(shù)圖像、統(tǒng)計(jì)圖等，空間與圖形部分更是處處有圖.在解答問題時(shí)，除了讀圖外，還需要畫圖.在數(shù)學(xué)課堂上，教師可引導(dǎo)學(xué)生從題目中獲取信息，幫助學(xué)生合理分析問題，采用豐富的教學(xué)方法，合理挖掘題目中的圖形資源，對(duì)圖形進(jìn)行合理“變身”，如此便能夠取得良好的教學(xué)效果.

一、通過畫圖鞏固與掌握基礎(chǔ)知識(shí)

掌握數(shù)學(xué)基礎(chǔ)知識(shí)是運(yùn)用數(shù)學(xué)知識(shí)解決問題的重要前提，學(xué)生錯(cuò)解或無法解答的主要問題在于沒有正確理解并掌握基礎(chǔ)知識(shí).因此在教學(xué)中，教師可引導(dǎo)學(xué)生在畫圖的過程中深入理解基礎(chǔ)知識(shí)，相較于傳統(tǒng)的教學(xué)方說，此種方式更容易被學(xué)生所接受.

例如，在教學(xué)“無理數(shù)概念”時(shí)，教師就可對(duì)學(xué)生進(jìn)行引導(dǎo)，如圖1，先畫出兩個(gè)邊長(zhǎng)為1的正方形，將這些圖形沿著一條對(duì)角線剪開，組成一個(gè)大的正方形.

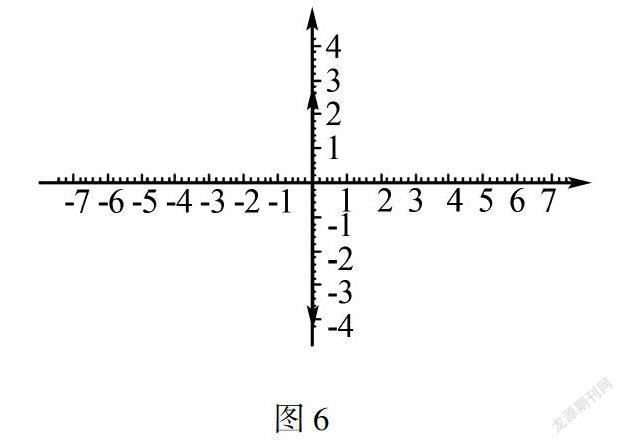
此時(shí)教師就可提出問題，對(duì)學(xué)生進(jìn)行引導(dǎo)：“大正方形面積是多少？”學(xué)生立刻回答：“2”.教師可繼續(xù)提問：“非常正確，那么假如大正方形的邊長(zhǎng)為a，那么a2=2，a是有理數(shù)嗎？”此時(shí)學(xué)生陷入了思考，教師可對(duì)學(xué)生進(jìn)行啟發(fā)：“想要說明a是不是有數(shù)，我們應(yīng)當(dāng)先看a是不是能夠表達(dá)為有限小數(shù)或無限循環(huán)小數(shù)，即分?jǐn)?shù).”經(jīng)過教師的啟發(fā)，學(xué)生紛紛開動(dòng)腦筋，有的學(xué)生說：“因?yàn)?2=1，22=4，因此a是大于1且小于2的數(shù).”有的學(xué)生說：“因?yàn)?2×32=94，因此a不是32.因?yàn)?3×43=169，53×53=259，因此a也不是43、53…”教師可對(duì)學(xué)生進(jìn)行的思路進(jìn)行肯定，同時(shí)繼續(xù)啟發(fā)學(xué)生：“我們可以量一量圖，用量出來的結(jié)果，即近似值來算一下.”學(xué)生得出了如下結(jié)果：“因?yàn)椤?.5×1.5=2.25，1.4×1.4=1.96，因此1.4

教師肯定了學(xué)生的想法后，就可對(duì)問題進(jìn)行拓展：“那么圓周率π也可以借助數(shù)軸上的點(diǎn)來體現(xiàn)嗎？我們是不是可以借助上面的方法來解答問題？”學(xué)生思想考后回答：“我們可先做一個(gè)直徑為1個(gè)單位長(zhǎng)度的圓片，周長(zhǎng)為π，然后將圓片上的點(diǎn)A放在原點(diǎn)，同時(shí)將圓片沿著數(shù)軸的正方向滾動(dòng)一周，點(diǎn)A到達(dá)的位置點(diǎn)A’表示的數(shù)即為π，如圖3.”

最后由教師進(jìn)行總結(jié)：“本堂課我們認(rèn)識(shí)了無理數(shù)，通過計(jì)算我們認(rèn)識(shí)到了其屬于無限不循環(huán)小數(shù)，而通過畫圖，我們發(fā)現(xiàn)了它的存在形式，還掌握了其在數(shù)軸上的表示方法.”無理數(shù)的概念較為抽象，通過畫圖就能夠幫助學(xué)生更好的體會(huì)到它的內(nèi)涵.可見，通過畫圖，學(xué)生就能夠直觀并深入的理解數(shù)學(xué)基礎(chǔ)知識(shí)，因此在課堂上教師應(yīng)當(dāng)把握時(shí)機(jī)，將數(shù)學(xué)知識(shí)與畫圖方法結(jié)合起來，便可提高課堂的教學(xué)質(zhì)量.

二、分析解題思路繪畫圖形鞏固與掌握了基礎(chǔ)知識(shí)后，教師就可帶領(lǐng)學(xué)生進(jìn)行畫圖解題訓(xùn)練.初中數(shù)學(xué)的各個(gè)板塊，都會(huì)涉及到圖形內(nèi)容，因此在課堂上，教師不僅要交給學(xué)生靈活的解題思路，同時(shí)還需提醒學(xué)生通過畫圖來解決問題，可從以下幾方面著手：

第一，帶領(lǐng)學(xué)生熟悉具體的解題步驟與程序.在具體教學(xué)中，教師應(yīng)當(dāng)多挑選一些針對(duì)性的例題進(jìn)行示范講解，重點(diǎn)突出畫圖解題的便捷性，在教學(xué)中，教師可對(duì)具體的解題步驟進(jìn)行分析與總結(jié)，經(jīng)過反復(fù)練習(xí)，學(xué)生自然能夠掌握解題的方法，同時(shí)也能夠體會(huì)到畫圖的作用，從而有效提高學(xué)生的解題效率.教師在課堂上可借助創(chuàng)新作圖的方法來對(duì)學(xué)生進(jìn)行引導(dǎo)，例如在解答與三角形有關(guān)的題目時(shí)，教師就可帶領(lǐng)學(xué)生使用彩筆等工具來作圖.

例如，在△ABC中，已知AB=AC，AD⊥BC于D點(diǎn)，而圖4中P是AB上的任意一點(diǎn)，請(qǐng)你使用無刻度直尺在AC上尋找點(diǎn)P1，使AP=AP1.

解答此類問題的基本思路是將圖中的CP連接起來，相交AD于H，同時(shí)連接BH并延長(zhǎng)交AC于P1，通過說明△ABP1約≌△ACP就能夠證明AP=AP1，見圖5.

第二，遵循循序漸進(jìn)的原則，強(qiáng)化學(xué)生的畫圖解題能力.為了有效提升學(xué)生的畫圖解題能力，教師需結(jié)合學(xué)生的具體情況來調(diào)整教學(xué)策略，遵循循序漸進(jìn)的原則，結(jié)合學(xué)生思維發(fā)展水平來進(jìn)行畫圖教學(xué).對(duì)于七年級(jí)的學(xué)生來講，畫圖解題的目標(biāo)可適當(dāng)放低，讓學(xué)生看懂線段圖，同時(shí)能夠結(jié)合線段圖來列出算式即可;對(duì)于八年級(jí)的學(xué)生來講，則可要求學(xué)生按照?qǐng)D形來分析應(yīng)用題的數(shù)量關(guān)系，學(xué)會(huì)解決一些實(shí)際問題.因?yàn)榘四昙?jí)的學(xué)生已經(jīng)有了一定的知識(shí)儲(chǔ)備，教師可引導(dǎo)學(xué)生結(jié)合題意畫圖解題，例如某水庫(kù)在今年四六月雨季時(shí)，水位升高了3m，而到了七月時(shí)，水位下降了-4m，那么這4個(gè)月以來，水位經(jīng)歷了多少m變化？

圖6在教師的引導(dǎo)下，學(xué)生通過對(duì)數(shù)軸圖中的數(shù)量關(guān)系進(jìn)行分析，順利得出了答案，水庫(kù)經(jīng)歷了7m的變化.可見畫圖解題不僅屬于一種必備技能，同時(shí)也是觀察與實(shí)踐的過程，在打好基礎(chǔ)知識(shí)的條件下，教師應(yīng)當(dāng)恰當(dāng)安排畫圖解題練習(xí)，有效提高學(xué)生的綜合素養(yǎng).

總而言之，畫圖對(duì)于解決數(shù)學(xué)問題來說具有非常重要的作用，學(xué)生通過畫圖能夠?qū)?shù)學(xué)知識(shí)簡(jiǎn)化，使抽象的條件變?yōu)閷W(xué)生更容易理解的形象內(nèi)容.因此在課堂上，教師應(yīng)當(dāng)先幫助學(xué)生鞏固基礎(chǔ)知識(shí)，開展多樣化的教學(xué)活動(dòng)，加強(qiáng)實(shí)踐，由此提高數(shù)學(xué)教學(xué)的有效性.

參考文獻(xiàn)：

[1]明廷軍.關(guān)注圖形平移過程掌握?qǐng)D形變化規(guī)律——微課教學(xué)的實(shí)踐探索[J].中學(xué)數(shù)學(xué)研究（華南師范大學(xué)版），2020（18）：48-50.

[2]許雯.對(duì)初中數(shù)學(xué)圖形等面積拼接問題的教學(xué)反思[J].北京教育學(xué)院學(xué)報(bào)（自然科學(xué)版），2012，7（04）：54-56+68.

[3]陳德燕.數(shù)學(xué)核心素養(yǎng)理念下的立體幾何教學(xué)——以“直線與平面垂直的性質(zhì)”為例[J].數(shù)學(xué)通報(bào)，2017，56（02）：36-38+44.

[4]王一新.初中數(shù)學(xué)反思性學(xué)習(xí)習(xí)慣的培養(yǎng)——以幾何教學(xué)為例[J].科學(xué)咨詢（教育科研），2020（03）：159.

[責(zé)任編輯：李 璟]