數形結合，以形助學

陳子燁

摘 要：數與形是數學中兩個最基本的研究對象，它們在一定條件下可以相互轉化。 教育心理學家皮亞杰所劃分的兒童認知發展階段的第三個階段是具體運算階段 （7～12歲）， 小學期間孩子們的具體運算思維一般還離不開具體事物的支持。本文以五年級數學“植樹問題”一課進行探究，數形結合的思想可以使某些抽象的數學問題直觀化、具體化、生動化，把抽象思維化為具象思維，有助于把握數學問題的本質 ，更好地做到“以數解形”和“以形助數”。

關鍵詞：轉化;認知發展;具體化;數形結合

“植樹問題” 一課是人教版五年級上冊《數學廣角》中的內容。“植樹問題”通常是指沿著一定的路線植樹，這條路線的總長度被樹平均分成若干段（間隔），由于路線的不同、植樹要求的不同，路線被分成的段數（間隔數）和植樹的棵數之間的關系也就不同。像這些課堂上難以讓學生親身去感受的生活實際問題，我們可以借助線段圖等手段讓學生從中發現一些規律，抽取出其中的數學模型，然后再用發現的規律來解決生活中的實際問題。

（一）在學生認知基礎上設計學習活動

學生從小學一開始就會接觸數形結合的方法。一年級學習10以內數相加減，老師就會用小棒或者其他圖案來代替數字，通過數一數擺一擺等方法學習簡單的加減法;二年級學習簡單的乘除法，老師也會借助具體物體來數一數擺一擺分一分輔助教學;三年級認識面積，老師會請來“小方格”幫助學生計算面積;四年級學習條形統計圖，讓學生學會使用圖形的變化表示數據的增減。學生在學齡階段的學習一直貫穿著數形結合的思想方法，因此在設計學習活動時，我們要把幾何直觀作為解決植樹問題的重要手段。“植樹問題”中的“公共汽車站”“架設電線桿”“敲鐘問題”“設置飲水點”“鋸木頭”“項鏈上的水晶”等問題，可以引導學生借助線段圖或示意圖進行直觀理解。

（二）認知沖突，引發思考

書本例題1是“同學們在全場100m的小路一遍植樹，每隔5m栽一棵（兩端要栽），一共要栽多少棵樹？”很多同學看題后的第一想法就是“每隔5m栽一棵，也就是栽100÷5=20（棵）”，這時老師提出疑問“這個想法對嗎？我們檢驗一下。”學生帶著問題和想法去驗證，可以先用比較簡單的例子來驗證，由淺入深。

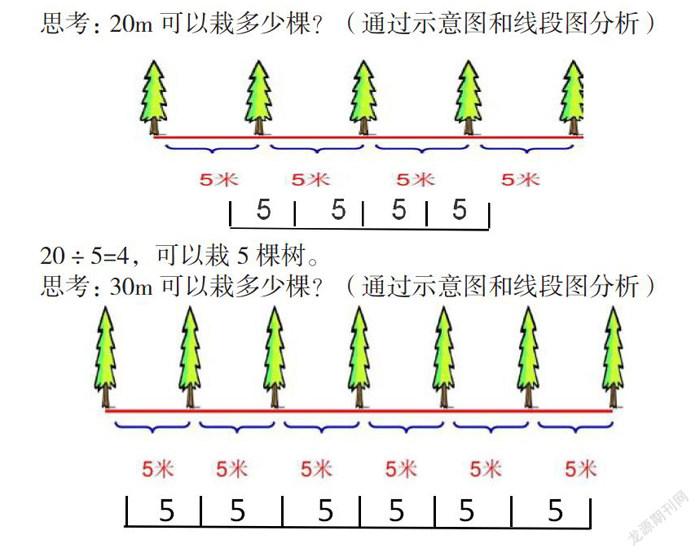
思考：20m可以栽多少棵？（通過示意圖和線段圖分析）

20÷5=4，可以栽5棵樹。

思考：30m可以栽多少棵？（通過示意圖和線段圖分析）

30÷5=6，可以栽6棵樹。

通過以上兩個例子，發現了什么？開始的想法是否正確？通過觀察和計算不難發現， 20÷5=4這里的4不代表4棵，而是代表4個間隔或者4份。因此原題100÷5=20中的20不代表20棵，而是代表20個間隔或者20份。通過兩個簡單的例子加以驗證，可以發現如果兩端都要栽樹，栽樹的棵數比間隔數要多1，從而建立起一條線段兩端都栽這類植樹問題的數學模型。

（三）逆向應用，知識遷移

學生明確題目信息“100m”是全長，“5m”是間隔長，“20”是間隔數，“21”是要栽的棵數。當題目變式為“園林工人沿一條筆直的公路一側植樹，每隔6m種一棵，一共種了36棵，從第一棵到最后一棵的距離有多遠？”學生讀題時明確這一題是已知樹的棵數求路線長度， 36棵樹也就是有35個間隔，因此總長度應該用35×6=210米。

書本例題2是“大象館和猴山相距60m。綠化隊要在兩館間的小路兩旁栽樹（兩端不栽），相鄰兩棵樹之間的距離是3m。一共要栽多少棵樹？”例2是在例1的基礎上進行教學的。學生可以利用例1發現的規律和化歸的思想進行思考，猜測兩端不栽應該是用間隔數減1。

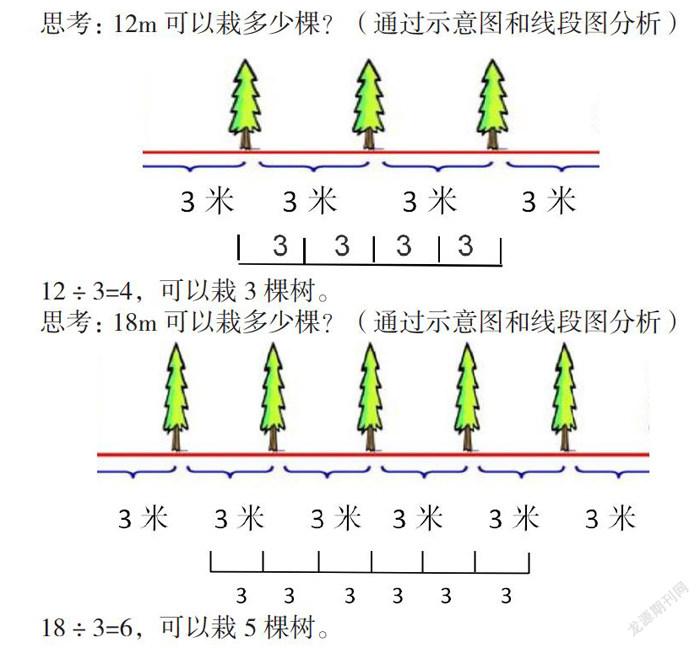
思考：12m可以栽多少棵？（通過示意圖和線段圖分析）

12÷3=4，可以栽3棵樹。

思考：18m可以栽多少棵？（通過示意圖和線段圖分析）

18÷3=6，可以栽5棵樹。

通過以上兩個例子，可以驗證最初的猜想。通過示意圖和線段圖，更加直觀地呈現出當兩端不栽時，要栽的棵數比間隔數少1。教師可根據教學情況，鼓勵學生用自己的方法探索規律，讓學生在知識遷移和轉化中學習解決問題的方法。

（四）數形結合，化曲為直

書本例題3是“張伯伯準備在圓形池塘周圍栽樹。池塘的周長是120m，如果每隔10m栽一棵，一共要栽多少棵樹？”區別于例1例2在筆直的線段上植樹，這是一條首尾封閉的曲線上植樹的問題。通過前兩個例題，學生已經有了解決這類問題的一般方法和建立數學模型的能力，引導學生先從簡單情況入手。

通過數形結合，化曲為直的方法，學生聯系已有的知識可以發現這種“封閉曲線”的規律，即栽樹的棵數正好等于間隔數，相當于一端栽，一端不栽，從中滲透了轉化的數學思想。學習了3個例題后，教師可引導學生借助示意圖或者線段圖將三種情況進行對比和分析，方便學生理解和記憶。教學中要強調畫圖的策略，充分運用數形結合的方法進行理解和總結。讓學生意識到養成畫圖的習慣是非常重要的，他們平時在解決數學問題遇到困難時，可以借助畫圖幫助理解。

（五）教學思考

新課標中強調“以學生為主體”，體現學生的主體性。如果教師一下子把三種情況直接總結出規律，學生可以快速區分植樹問題的是三種情況，但學生在碰到問題是只會對號入座，照葫蘆畫瓢，無法發展數學思維和解決問題的能力。生生間的合作交流是課堂的推動力，數形結合是學生構建知識的一個拐杖，讓學生從“發現規律”到“運用規律”，做到思維方法的真正滲透。植樹問題只能是種樹嗎？生活中路燈的安裝、上樓問題、敲鐘問題、鋸木問題等都可以運用本節課知識，拓展了知識的外延。

“數缺形時少直覺，形少數時難入微;數形結合百般好，隔離分家萬事非。”華羅庚這四句詩很好地表現出數形結合的重要性。要想在解決問題中有效地實現數形結合，首先要明確“數”與“形”的結合點。幾何圖形具有直觀具體的特點，化抽象為具象，利用幾何圖形解決問題，往往能產生事半功倍的效果。我們既能把“數”化為“形”去理解，也能從“形”總結“數”的規律。從“植樹問題”這一課中，我們通過把例題信息轉化成示意圖和線段圖理解了三種不同情況，也從這些圖中建立了形象的數學模型，總結出相應的計算規律。

對于小學生來說，理解和消化的過程一定要把問題具象化、簡單化。本課除了運用數形結合的方法，還巧妙地加入“歸化”思想幫助理解。從簡單的例子入手，學生容易理解，從而獲得成功的體驗，增加了學生繼續探究的動力。再通過小組合作進行問題猜測、檢驗、得出結論，逐步形成自主解決問題的能力。學生一旦掌握了數形結合的方法，平常遇到難題的時候不斷嘗試、運用，從而發現“數”與“形”的奧妙，提高數學思維能力。

本文系廣州番禺區教育規劃十三五專項課題《基于研學后教理念下小學數學“助學課堂”模式的研究》（課題編號：2018-zx269）階段性成果。