一種改進的種子擴展的重疊社區檢測算法

段瑞瑋 張公敬

摘要：針對基于種子擴展的重疊社區檢測算法存在因種子選取質量不高而導致重疊社區檢測結果準確度較低的問題，提出一種利用圖嵌入、聚類和K-shell相結合的新的種子選取策略來進行種子擴展的重疊社區檢測算法。算法利用提出的新的種子選取策略得到種子集，根據社區度量函數即電導性最優的原則不斷進行種子擴展完成社區劃分。研究結果表明，改進的種子擴展的重疊社區檢測算法提高了檢測結果的準確度。

關鍵詞：重疊社區;圖嵌入;聚類;K-shell;種子擴展;社區檢測

中圖分類號：TP391

文獻標志碼：A

文章編號：1006-1037（2021）01-0064-06

基金項目：國家自然科學基金（批準號：61872205）資助。

通信作者：張公敬，男，副教授，主要研究方向為數據挖掘、智能信息處理、信息安全等。E-mail：zhang8887327@163.com

復雜網絡是具有大量節點和連接的網絡，社區是節點內部連接緊密而外部連接相對稀疏的一組節點集群，社區檢測可以發現由相似屬性節點組成的密集集群。在非重疊社區結構[1]中，網絡里的每個節點只能屬于一個社區，隨著對復雜網絡的深入研究，人們逐漸發現重疊社區更加符合個體在現實網絡中存在的規律，其中同時參與多個社區的節點被稱為重疊節點，因此，對重疊社區發現研究的關注度越來越高。當前被最廣泛應用的重疊社區檢測算法主要分為三類：基于標簽傳播的重疊社區檢測算法[2-3]，這類算法根據節點的大多數鄰居節點的標簽為其添加標簽以代表所屬的社區，但是檢測結果不穩定;基于節點相似度的重疊社區檢測算法[4-5]，基本思想是網絡中越相似的節點越容易聚集成群，相對于基于標簽傳播的重疊社區檢測算法，穩定性有了提高，但是時間復雜度較高;基于種子擴展的重疊社區檢測算法[6-7]，核心思想是找到好的種子，然后基于社區度量函數貪婪地擴展種子，直至完成社區檢測。相對于前兩類重疊社區檢測算法，在穩定性和時間復雜度上有了明顯提高，也適用于大型網絡。基于種子擴展的重疊社區檢測算法又可分為兩類：基于種子擴展的局部重疊社區檢測算法，例如，Hollocou等[8]提出的通過擴展初始給定種子集來檢測多個可能重疊的局部社區的Mutilcom算法，但僅可識別出與給定種子集相關的局部社區，不能全面了解網絡的信息從而提供實際應用價值;基于種子擴展的全局重疊社區檢測算法，例如，Whang等[9]提出的NISE算法，首先對節點進行過濾，然后通過新的播種策略找到好的種子，最后進行種子擴展完成社區檢測。這類算法可全面了解網絡的信息，準確識別網絡中所有社區的組織和功能，從而提供更加完善的實際應用價值。但是其普遍存在的問題是對選取的種子節點敏感，種子的質量對最終社區檢測效果影響較大。基于種子擴展的全局重疊社區檢測算法出現的問題，本文對如何在網絡中找到高質量的種子進行重疊社區檢測的方法做了改進，提出一種改進的種子擴展的重疊社區檢測算法（Graph-embedding clustering seed expansion， GCSE）。

1 方案

1.1 問題定義，相關知識和社區質量評價標準

社區是一組連接緊密的節點集群，這些節點內部的相互連接密度高于與外部節點的連接密度。給定無向無權圖G=（V，E），圖中節點集用V表示，邊集用E表示。將此無向圖表示為鄰接矩陣M，M矩陣是對稱的，Mij=0時，表示節點i與節點j之間無邊相連，Mij=1時，表示節點i和節點j之間有邊相連。重疊社區檢測問題的目標是將圖劃分為k個簇，這k個簇之間存在重疊現象，這些簇內節點集合滿足T1∪T2∪…∪TkV關系。

判斷網絡中節點的重要性程度有很多種方法，如度中心性、介數中心性、接近中心性， K-shell[10]分解算法等。其中度中心性忽略了節點的鄰居對節點影響力起到的間接作用，介數中心性和接近中心性未將節點的拓撲位置考慮進去來綜合評判節點的重要性，而K-shell分解算法考慮節點的拓撲位置，可以根據節點的影響力得到較粗粒度的排序結果，為此，本文借助該算法得到網絡拓撲核心節點集，通過提出的節點影響力評判標準得到核心節點集中影響力最大的節點。

本文用社區質量評價標準NMI[11]來衡量算法社區檢測的效果

其中，N表示節點數量，A表示已知社區分布，B表示檢測到的社區分布，C是一個混淆矩陣，矩陣中的元素Cij表示既屬于A中i社區也屬于B中j社區的節點的數量，CA是已知的社區數量，CB是檢測到的社區數量，Ci（Cj）為社區C第i行（第j列）的節點數量之和。

用電導性[9]（conductance）作為衡量單個社區質量的評價標準

1.2 重疊社區檢測算法GCSE

本節提出一種改進的種子擴展的重疊社區檢測算法GCSE。

1.2.1 圖中節點表示為向量 本文應用了圖嵌入算法DeepWalk[12]，是一種將隨機游走（random walk）和word2vec兩種算法相結合的圖結構數據挖掘算法。該算法能夠學習網絡的隱藏信息，將圖中的節點表示為一個包含潛在信息的向量，該算法主要分為隨機游走和生成表示向量兩個部分。通過該算法將圖中節點表示為向量后，根據節點在嵌入空間中的相互距離進行聚類。

1.2.2 基于可變密度的聚類算法對節點進行聚類 將上一節得到的向量利用聚類算法得到簇。已有的聚類算法DBSCAN[13]首先將數據點集中的每個節點標記為未處理對象，人工輸入半徑參數Eps和密度閾值MinPts，然后計算每個節點Eps半徑內節點的個數，若Eps半徑內節點的個數多于密度閾值MinPts，則標記這個節點為核心點，在核心點鄰域內剩余的點則被標記為邊界點，否則將被標記為噪聲點。如果該算法的半徑參數Eps和密度閾值MinPts選擇不合理將會使得聚類準確率降低。為此，本文提出基于可變密度的聚類算法（Variable density-Based Spatial Clustering of Applications with Noise， VDBSCAN），根據節點在嵌入空間中的相互距離利用VDBSCAN進行聚類得到簇D1，D2，…，Dk，以提高聚類準確率。

首先給定參數Eps，按照每個節點Eps半徑內的節點個數對節點從大到小排序，對于Eps半徑內節點個數相同的節點，利用高斯核相似度更細化的區分節點之間的局部密度。高斯核相似度定義

其中，de的值為半徑參數Eps，dij為半徑Eps范圍內的點i到點j的距離，Ir表示節點i半徑Eps范圍內的所有節點。按照局部密度的大小對每個節點從大到小排序，選取局部密度最大的節點做核心點，按照該點成為核心點的密度閾值MinPts并結合之前給定的半徑參數Eps繼續擴展聚類。之后，在未被處理的節點中選取密度最大的點做核心點，重復上一步，直到剩余的節點無法作為核心點停止（即剩余未處理的節點在其半徑Eps范圍內節點的個數小于4）。最后，形成簇D1，D2，…，Dk，對于節點個數不足3個的簇，將其合并到與它距離最近的簇中，聚類結束。

1.2.3 選取種子 將上一節形成的簇D1，D2，…，Dk分別利用K-shell劃分層次，找到每個簇的核心節點集，如果核心節點集中只有一個節點，則這個節點作為新的種子加入種子集S。如果核心節點集中包含多個節點，則需要詳細區分具有同一K-shell值的節點的影響力。本文使用下列公式對節點的重要性程度進行排序，選出重要性程度最高的節點作為新的種子加入種子集S

將加權網絡中的邊權概念引入無向無權網絡中，邊權Wij值定義為一條邊的兩端節點的度數之和，其中di為節點i的度數，dj為節點j的度數。

節點的點權又稱為點強度（Vertex Strength），定義為與節點相連的邊權之和，Ni為節點i的直接相連節點的集合。

其中，Ti表示節點i的鄰域聚類緊密程度，反映了節點i的直接鄰居之間的連接緊密程度，Ei為節點i的Ki個直接鄰居之間的連邊個數。

其中，Fi是點i及其直接鄰居對鄰域的影響力。

其中，MNi表示節點i的影響力大小，節點i的MNi值越大則說明節點i在其鄰域中影響力越大。經過上述步驟可以得到各個簇D1，D2，…，Dk的核心節點集中影響力最大的節點，將這個節點作為新的種子節點添加到種子集S中。

1.2.4 種子擴展 利用Personalized PageRank [8]評分函數對種子集S中的每個新種子節點s的鄰域節點進行打分，得到每個節點的得分向量fs。按照fs分值從高到低的順序，根據電導性依次判斷節點是否要加入當前種子所在的局部社區，當節點加入社區使得當前社區電導性更優時，將該節點劃分到這個社區，再按順序依次檢查其他節點的加入會不會引起社區電導性的變化，最后返回達到電導性最優的集群。

1.2.5 社區合并 在社交網絡中，一個節點通常同時參與多個社區，所以由GCSE算法返回的社區可能存在重疊現象。在GCSE算法的末尾增加了一個名為合并的處理步驟。如果兩個社區之間重疊節點過多，則進行社區合并;如果仍存在重疊節點，根據該節點的加入和刪除對當前所在社區電導性變化量的影響來判斷該節點的歸屬，哪個社區的電導性的變化量最大，將節點歸于該社區;對于未被分配社區的節點按照電導性繼續為其分配社區，直到圖中所有節點都劃分完成。

1.2.6 GCSE算法描述 算法的輸入為一個無權無向圖，最終輸出結果為檢測到的社區。

Step 1 通過圖嵌入算法DeepWalk將節點表示為向量;

Step 2 用改進的自適應參數密度聚類算法VDBSCAN對通過Step 1形成的數據點集進行聚類，形成簇D1，D2，…，Dk;

Step 3 在簇D1，D2，…，Dk中借助K-shell劃分出核心節點集，從核心節點集中選出影響力最大的節點作為種子，加入種子集S;

Step 4 根據Step 3選取的種子集，利用Personalized PageRank評分函數對其余節點進行評分，并對其降序排序，按照排序結果利用電導性來獲取各個種子對應的局部社區;

Step 5 如果兩個局部社區之間重疊節點過多則對其進行社區合并。若圖中仍存在重疊節點和未被分配的節點，則根據電導性為其分配社區，直到社區中所有節點劃分完成，并返回最終的社區檢測結果。

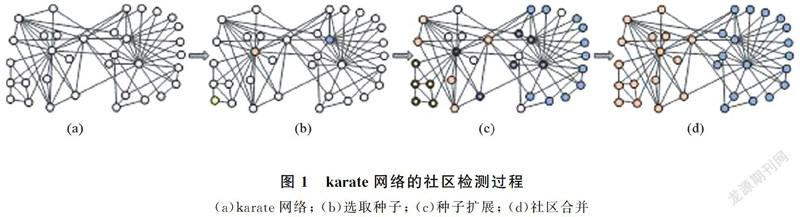
karate網絡[14]是網絡分析領域的經典數據集，由34個節點組成，實際上劃分為2個社區。本文在karate網絡上應用算法GCSE進行社區檢測過程如圖1所示。

2 實驗

2.1 實驗環境描述和參數設置

實驗在Intel （R） 3.6GHZ Xeon（R） W-2133CPU和32G RAM的電腦上運行，軟件平臺為Windows下的Python 3.6。GCSE算法中使用了2個參數：d和MinPts。圖嵌入DeepWalk算法將網絡中的每個節點通過Word2vec表示為一個維度為d的向量，本文將維度d設置為2。VDBSCAN聚類算法中密度參數MinPts用于控制檢測的初始化社區數量，通過參數調整得知將其設置為0.46時較為合適。

2.2 實驗結果和分析

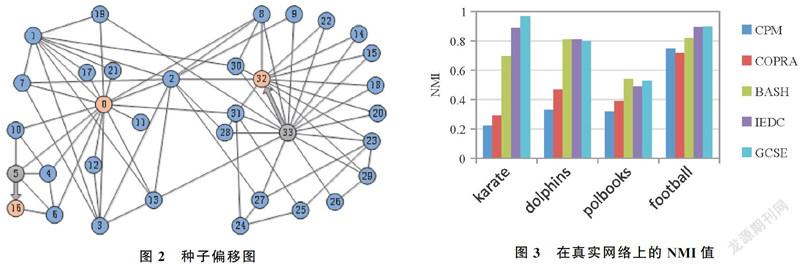
2.2.1 真實網絡 如圖2所示，在Karate網絡上通過度中心性查找到的種子為0、5、33，而GCSE通過綜合考慮節點的拓撲位置和影響力查找到的種子為0、16、32，在實驗中也證明了通過這種方法查找到的種子的質量比較高，提高了社區檢測的準確性。實驗中，將GCSE算法與算法CPM[15]，COPRA，BASH[16]，IEDC[17]分別在真實網絡karate，dolphins，polbooks和football上進行了比較。

圖3顯示了在真實網絡上不同算法的NMI值，GCSE算法在四個真實網絡上可以得到良好的社區檢測效果。GCSE算法在karate網絡表現最好，其次是在football網絡上的表現也優于其他算法，得到的社區檢測結果非常接近真實情況。

2.2.2 仿真網絡 除了真實網絡，使用了LFR （Lancichinetti-Fortunato-Radicchi）基準網絡測試了GCSE算法的性能。其中，仿真網絡節點的最大度數設置為50，社區節點個數最小值設置為20，社區節點個數最大值設置為50，節點平均度設置為10。本文研究了不同算法取不同μ值和不同On值時的性能，對應的2組仿真網絡參數設置如下： AD1： N=6 000， Om=3， On=50， μ=0.0～0.4; AD2： N=6 000， Om=3， On =50～400， μ=0.2。

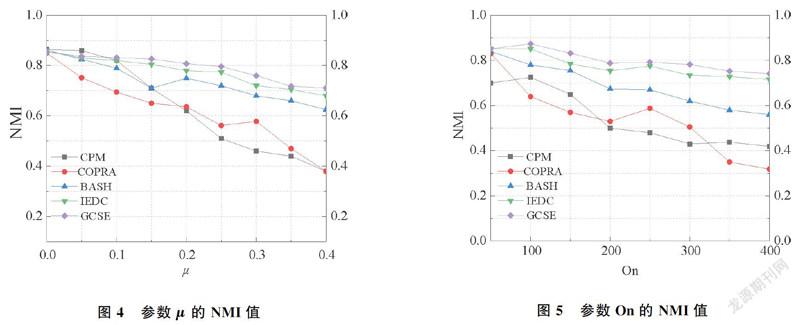
圖4為各算法在AD1仿真網絡上的實驗結果，顯示了μ在由0增加到0.4時，不同算法的NMI值。μ表示社區結構的重疊度，當μ=0時，所有算法的性能都很好，NMI值接近于1。隨著混合參數μ的增加，所有算法的性能下降，但是GCSE算法仍然表現出良好的魯棒性，IEDC算法也表現出了較好的性能。

圖5為各算法在AD2仿真網絡上的實驗結果。顯示了On從50增加到400時，不同算法的NMI值。On表示社區中重疊節點的數量，實驗結果表明，隨著On值的增加，即隨著網絡中重疊節點數量的增加，所有算法的效率和精度均降低，但GCSE算法仍優于其他算法，最糟糕的是COPRA算法。

3 結論

本文提出了一種改進的種子擴展的重疊社區檢測算法GCSE。首先提出一種新的種子選取策略，該策略為利用圖嵌入將節點表示為向量，接著利用提出的可變密度的聚類算法VDBSCAN對節點進行聚類，改進后的聚類算法對不同密度節點集群的適應性更強，考慮節點的拓撲位置以及節點鄰居對節點影響力起到的間接作用來綜合評判節點影響力。按照提出的新的種子選取策略從每個簇中選取種子，利用Personalized PageRank評分函數對節點進行評分，最后根據評分結果利用電導性擴展種子完成社區檢測。實驗結果表明，該算法提高了選取的種子的質量和社區檢測的準確性。

參考文獻

[1]LIU Z， MA Y. A divide and agglomerate algorithm for community detection in social networks[J]. Information Sciences， 2019（482）： 321-333.

[2]GREGORY S. Finding overlapping communities in networks by label propagation[J]. New J. Phys.， 2009（12）： 2011-2024.

[3]朱帥， 許國艷， 李敏佳，等. 基于LeaderRank的重疊社區發現算法[J]. 計算機與現代化， 2019， 283（3）：94-98.

[4]SUNGSU L， SEUNGWOO R， et al. LinkSCAN*： Overlapping community detection using the link-space transformation[C]// 2014 IEEE 30th International Conference on Data Engineering. Chicago， 2014： 292-303.

[5]BAI L， CHENG X， LIANG J， et al. Fast graph clustering with a new description model for community detection[J]. Information Sciences， 2017（388）： 37-47.

[6]李艷， 賀靜， 武優西. 種子節點貪婪擴張的重疊社區發現方法[J]. 小型微型計算機系統， 2019， 40（5）：205-209.

[7]於志勇， 陳基杰， 郭昆， 等. 基于影響力與種子擴展的重疊社區發現[J]. 電子學報， 2019， 47（1）：153-160.

[8]HOLLOCOU A， BONALD T， LELARGE M. Multiple local community detection[J]. ACM Sigmetrics Performance Evaluation Review， 2018， 45（3）： 76-83.

[9]WHANG J， GLEICH F D， DHILLON I. Overlapping community detection using neighborhood-inflated seed expansion[J]. IEEE Transactions on Knowledge and Data Engineering， 2016， 28（5）： 1272-1284.

[10] BONACICH P. Factoring and weighting approaches to status scores and clique identification[J]. Journal of Mathematical Sociology， 1972， 2（1）： 113-120.

[11] ZHANG P. Evaluating accuracy of community detection using the relative normalized mutual information[J]. Computer Science， 2015（11）： 11006.

[12] PEROZZI B， Al-RFOU R， SKIENA S. Deepwalk： Online learning of social representations KDD[C]//20th ACM SIGDD International Conference on Knowledge Discovery and Data Mining. New York， 2014： 701-710.

[13] 歐陽佩佩， 趙志剛， 劉桂峰. 一種改進的稀疏子空間聚類算法[J]. 青島大學學報（自然科學版）， 2014， 27（3）：44-48.

[14] ZACHARY W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research， 1977，33（4）： 452-473.

[15] PALLA G， DERENYI I， FARKAS I， et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature， 2005， 435（7043）： 814-818.

[16] CUI Y， WANG X， EUSTACE J. Detecting community structure via the maximal sub-graphs and belonging degrees in complex networks[J]. Physica A： Statistical Mechanics and its Applications， 2014（416）： 198-207.

[17] HAJIABADI M， ZARE H， BOBARSHAD H. IEDC： An integrated approach for overlapping and non-overlapping community detection[J]. Knowledge-Based Systems， 2017（123）： 188-199.