基于序列模式的業務流程模型的預測對

齊陳榮

摘 要：為突破固定模式，實時預測，使流程管理更高效更準確，本文提出一種基于序列模式的對齊預算方法。以業務流程模型和日志集作為輸入，通過分析模型中活動的行為關系，將活動劃分為不同的序列模式，利用條件概率對序列模式中活動做預測。并且通過實例分析了該方法的有效性。

關鍵詞：Petri網;對齊;預測;序列模式;條件概率

中圖分類號：TP391.9 ?文獻標識碼：A ?文章編號：1673-260X（2021）07-0013-04

0 引言

隨著信息技術的快速發展，業務流程管理在企業或組織間扮演著越來越重要的角色。然而，真實的業務場景與流程模型間會存在行為不一致，我們經常使用對齊來描述這種差異。目前，國內外很多學者研究了對齊問題。例如，Bloemen V等[1]提出了不同于標準成本函數的新的成本函數，設計了優先考慮最大化同步移動對齊算法，該算法不同于A*算法和符號算法，最后通過實例說明了算法的實用性和有效性。Garcia-Banuelos L等[2]介紹了一種新的對齊方法，即通過兩個事件結構做糾錯同步積的對齊方法，并詳細闡述了日志與模型間的六種不匹配行為，通過一種自然語言來描述這個變化。劉靜[3]等人提取出事件日志有效的高頻形態學發生片段，在此基礎上發現最優跡對齊。前人在對齊方面的研究，大多是通過暴力搜索來尋找差異且日志與模型都具有完整性。因此，突破固定模式，實時預測，使流程管理更高效更準確顯得尤為重要。關于預測的研究有，Tax N等[4]提出了一種基于機器學習方法預測在給定的不完整序列之后可能出現的元素。Hamed R I[5]提出了一種基于模糊規則推理的模糊Petri網方法，通過實驗表明所提出的模型可以達到與現有軟件相匹配的置信值。Ma Z等[6]利用極小值和可達圖解決了有標識Petri網中的一個基本標識估計問題，提出了基礎標識的兩種概念，并證明對于一組警報是可預測的。

基于上述研究，本文提出了一種基于序列模式的業務流程模型的預測對齊方法。第1節通過動機例子引出本文方法;第2節介紹相關定義;第3節首先將活動劃分為三個序列模式，提高對齊效率。然后，利用條件概率預測下一節點的發生;第4節進行實例分析;最后總結全文并展望未來。

1 動機例子

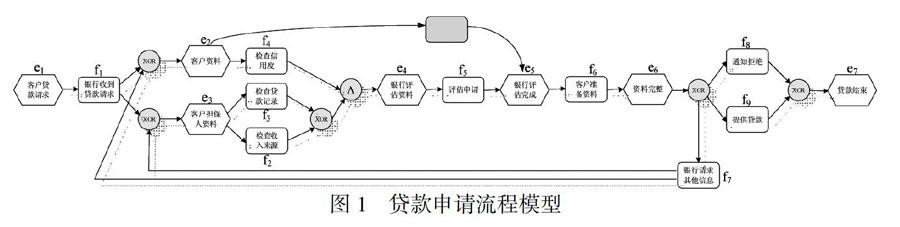
本節將利用某貸款申請流程來說明本文的研究動機，為了方便起見，將每個函數賦予新的標簽如表1所示，圖2是用EPC（事件驅動過程鏈）語言描述的貸款申請流程。流程從“銀行收到貸款申請”開始，兩個任務“檢查信用度”和“檢查收入來源”或“檢查信用度”和“檢查貸款記錄”并發，進入“評估申請”環節，或者直接進入“客戶準備資料”環節，然后兩個分支選擇發生“提供貸款”或者“通知拒絕”，最后以“貸款結束”完成整個貸款流程。

考慮日志L={ACFI，AEFGI}，常見的兩種對齊方式有基于A*最短路徑算法的最優對齊和最大化同步移動對齊。我們認為這兩種對齊方法并不總是合適的，（1）A*算法旨在以暴力搜索的方式尋找最短路徑以達到成本最低的對齊如γ1，可以看出通過跳過活動C以達到成本最低，但在真實業務場景中，無法判定活動C是否應該發生，若活動C發生如γ2。（2）最大化同步移動對齊旨在盡量使日志與模型對齊以減少跳過移動，進而達到成本最低如γ3，在模型中活動G是進入循環的標志性活動，若進入循環體如γ4。針對這兩種問題，本文提出一種基于序列模式的預測對齊方法，這種方法不僅能預測下一個發生的節點，還能更高效更準確地進行預測。

2 基本概念

定義1[7，8]（業務流程Petri網） 一個網PN=（P，T;F）是業務流程Petri網，當其滿足以下條件：

（1）P為庫所集，有P≠？覫。

（2）T為變遷集，有T≠？覫。

（3）F=（P×T）∪（T×P）為流關系集。

在流程模型P的變遷之間存在一種弱序關系，即一對變遷（x，y）∈T×T是弱序關系，當且僅當存在一個發生序列？滓=t1t2…tn有（P，M0）[？滓〉，并且有i，j∈N，1≤i≤j≤n使得tj=x，ti=y，記作x？酆y。根據弱序關系定義模型和日志的行為輪廓關系[9]。

定義2[10]（模型的行為輪廓） 設P是一個流程模型，對？坌（x，y）∈P，則x，y的行為關系如下：

（1）嚴格序關系→P，若x？酆Py∧y≯Px，記作x→Py。

（2）交叉序關系||P，若x？酆Py∧y？酆Px，記作x||Py。

（3）排他序關系+P，若x≯Py∧y≯Px，記作+Py。

則稱集合BP{→P，||P，+P}是模型P的行為輪廓。

定義3[11]（序列模式） 流程模型P中的所有活動集A，序列？籽=∈A*是由活動組成的非空序列集，其中ak∈A。

定義4（依賴關系） 序列模式？祝=<<？琢1，？琢2，…，？琢k>，<？茁1，？茁2，…，？茁k>，<？酌1，？酌2，…，？酌k>>=<？琢i，？茁i，？酌i>，其中i=1，…，k。

？坌？琢k∈A，？堝？琢k∈？茁i，？酌i，st.？琢k？埸L，其中？琢i為長期依賴關系集，？茁i為長期沖突關系集，？酌i為長期選擇關系集，L為日志。

如圖2所示，活動a和活動g處于干路，即此活動必須出現在任意一條發生序列上，我們將其稱為長期依賴關系。然而，活動e和活動f只能有一個出現在發生序列中，即存在長期選擇關系，而活動h和活動i則不能同時出現在一條發生序列中，所以，兩者呈長期沖突關系。理解活動集合的劃分不僅是預測的基礎，還能通過劃分模型提高對齊效率。

3 序列模式的預測對齊

序列模式旨在分解流程，將流程模型中的活動按行為關系劃分為三個集合，即？祝=<？琢i，？茁i，？酌i>。在三個關系集合中，首先對齊？琢i中的集合，即長期依賴關系優先對齊;然后，在已對齊的活動中利用條件概率預測在集合？茁i中需要對齊的活動;最后，在沖突集合？酌i中找出與已對齊活動呈沖突關系的其他活動將其跳過。

算法1 （序列模式的劃分）

輸入：輸入流程模型P、日志的發生序列L=[li]。

輸出：基于序列模式的對齊li？蓯。

（1）輸入流程模型P，將流程模型中的活動劃分為三個活動集合？琢i、？茁i、？酌i，執行步驟（2）。

（2）從日志中選擇一條發生序列li，首先對齊在？琢i集合中的活動得到序列li′;然后以已對齊的活動為條件利用條件概率在？茁i集合中預測需要對齊的活動得到序列li″;最后在集合？酌i中找出與已對齊活動呈沖突關系活動，執行步驟（3）。

（3）將沖突的活動直接跳過，輸出一條基于序列模式的預測對齊序列li？蓯，算法結束。

由于算法2是在條件概率的基礎上進行的，因此，我們先引入條件概率定義。

定義5 （條件概率） 設A，B是兩個事件，且P（B）>0，P（A/B）為事件B發生的條件下事件A發生的條件概率。當B={B1，B2，…，Bn}，Bn≠？覫時，條件概率公式為P（A）=∑，有，P（A）=1-P（A）。

算法2 （基于條件概率的預測）

輸入：流程模型P、序列li′和集合？茁i。

輸出：集合？茁i中需要對齊的活動。

（1）輸入流程模型P和發生序列li′，執行步驟（2）。

（2）利用定義5的條件概率來判定集合？茁i中需要對齊的活動，執行步驟（3）。

（3）將序列li′中已對齊的活動作為條件，如果在此條件下該活動的發生概率大于1/2，則對齊該活動;如果在此條件下該活動不發生的概率大于1/2，則對齊與該活動成選擇關系的活動，算法結束。

4 案例分析

算法1和算法2詳細闡述了如何利用條件概率預測下一節點的發生，通過劃分序列模式，提高了對齊效率。本節將通過一個實例具體分析算法中所提到的方法，由于本文以EPC語義為背景，首先利用方賢文[12]提出的EPC誘導方法將其轉化為Petri網，如圖3。

考慮日志l1=ABCEFI，首先利用算法1將流程模型劃分為三個集合，？琢i=，？茁i=<？子2，CD？子1E;？子2，BD？子1E>，？酌i=對齊長期依賴關系得到li′;然后利用算法2判定A和F之間需要對齊的活動，從圖3中可看出，如果活動E發生，活動D和沉默活動？子1必須發生，因此在活動A和活動F已發生的條件下來判定活動E發生的概率。如圖3所示，當活動F發生時，庫所e5中必須存在一個由于觸發活動E或者？子2而產生的標識，即P（E/F）=1/2。在活動A被觸發后若要觸發活動E，沉默變遷？子1必須發生，即庫所e′和庫所e″中都有標識。觸發的A使庫所e2和e3都存在一個標識，活動D被觸發的概率為1/2，所以e′中存在標識的概率為1/2，而e″中存在標識的概率為1，所以P（E/A）=;最后，跳過所有在集合？酌i中未對齊的活動，得到l1″，如表3。

5 結束語

本文提出了一種基于序列模式的業務流程模型的預測對齊方法，它以流程模型和日志發生序列作為輸入，通過劃分序列模式將活動分成三個關系集。隨后利用條件概率在已對齊活動的情況下預測下一節點發生的概率。該方法打破了以成本和路徑為基礎的常規對齊方法，并提高了對齊效率，已進行的實例評估驗證了該方法在實踐中的適用性和可擴展性。

然而，我們的方法也有一定的局限性，它主要限制于有界的流程模型和完整的日志序列，對于無界的流程和序列，我們無法判斷。在未來工作中，需要對預測做進一步研究，并將其應用于Prom框架中。

參考文獻：

〔1〕Bloemen V， Zelst S J V， Aalst W M P V D， et al. Maximizing Synchronization for Aligning Observed and Modelled Behaviour： 16th International Conference， BPM 2018， Sydney， NSW， Australia， September 9-14， 2018， Proceedings[M]// Business Process Management. 2018.

〔2〕Garcia-Banuelos L， Van Beest N， Dumas M， et al. Complete and Interpretable Conformance Checking of Business Processes[J]. IEEE Transactions on Software Engineering， 2015：1-1.

〔2〕Luciano Garcia-Banuelos，Nick R T P van Beest，Marlon Dumas，et al. Complete and interpretable conformance checking of business processes[J]. IEEE Transactions on Software Engineering， 2018， 44（03）：262.

〔3〕劉靜，方賢文.基于成本對齊的業務流程變化挖掘方法[J].計算機科學，2020，47（07）：78-83.

〔4〕Tax N， Teinemaa I， Zelst S. An interdisciplinary comparison of sequence modeling methods for next-element prediction[J]. Software and Systems Modeling， 2020， 19（02）.

〔4〕Tax N， Teinemaa I， Zelst S. An interdisciplinary comparison of sequence modeling methods for next-element prediction[J]. Software and Systems Modeling， 2020， 19（02）.

〔5〕Hamed R I. Confidence value prediction of DNA sequencing with Petri net model[J]. Journal of King Saud University ¨c Computer & Information Sciences， 2011， 23（02）：79-89.

〔6〕Ma Z， Yin X， Li Z. Marking Predictability and Prediction in Labeled Petri Nets[J]. IEEE Transactions on Automatic Control， 2020， PP（99）：1-1.

〔7〕應麗，方賢文，王麗麗，劉祥偉.基于業務能力的可配置業務流程模型變化域分析[J].計算機科學，2019，46（10）：322-328.

〔8〕吳哲輝.Petri網理論[M].北京：機械工業出版社，2006.6-42.

〔9〕郝晉淵，孫丹丹，郝真鳴，陳凡，冉寧.基于標簽Petri網的自動制造系統初始資源配置優化[J].電子測量與儀器學報，2020，34（08）：30-36.

〔10〕郝惠晶，方賢文，王麗麗，劉祥偉.基于Petri網行為緊密度的有效低頻行為模式分析[J].計算機科學，2019，46（02）：321-326.

〔11〕M. Fani Sani， S.J. van Zelst， and W.M.P. van der Aalst. Applying Sequence Mining for Outlier Detection in Process Mining[J]. 2018.

〔12〕方賢文，彭珂，王麗麗，等.基于配置和撤銷狀態的業務流程變化傳播分析[J].計算機集成制造系統，2018，24（07）：1621-1630.