并發L-BFGS異構率定算法設計與實現

田在榮 李強 聶寧明 全婷

摘要：針對分布式水文模型在水文模擬參數率定過程中計算與收斂速度過慢的問題，提出一種面向異構平臺的水文模擬并發參數率定方法。對傳統的L-BFGS算法進行并發式改造使其結構適應并行計算的率定需求;對HIMS水文模型進行異構移植，使整個水文模型以多線程的形式并發運行于協處理器端;以拉薩河流域為例，在Intel+Nvidia GPU與國產AI加速器的雙異構平臺部署模型與測試算例。測試結果表明，并發L-BFGS異構率定算法適用于當前主流的“處理器+協處理器”架構，并能夠得到較好的率定效果。

關鍵詞：水文模擬;參數率定;HIMS;異構移植

中圖分類號：TP 338.6 文獻標志碼：A

文章編號：1006-1037（2021）03-0043-08

水文模型是對大自然中復雜的水文現象在計算機中的抽象化和概念化的展現[1]，是人們認識復雜的水循環運動過程和機制下的有效方法和手段。水文模型由眾多的物理模型如降雨入滲、蒸發散發、產流回流等具有特定物理意義的物理模型構成[2]，其中大多數物理模型都包含一系列流域相關的待定參數，而對水文模型進行參數率定就是通過確定當前所研究流域的待定參數值，最終完成對當前流域的建模。因此對模型參數率定是水文模擬過程的重要組成部分，參數選取的優劣直接影響到最終的模擬精度。而參數率定由于計算量大、耗時長，一直以來都是領域專家所必須面對的問題之一。早期研究水文模型時，參數率定的方法主要以人工試錯法[3]、自動優選參數法[4]為主。人工試錯法是根據以往積累的經驗選取一組參數，代入水文模型進行模擬計算，得到河流徑流量的模擬值，與觀測值對比，然后調整參數的取值，繼續對比模擬值和觀測值，直到模擬值和觀測值的誤差在允許的范圍，該組參數即為所求的最優參數組。人工試錯法受人為主觀影響較高[5]，且率定效率較低，實用性較差。自動優選參數法是通過設定計算機程序，使計算機根據設定的規則選取參數進行率定[6]。由于水文模型的運行依賴于流域內每個子流域內部眾多物理模型的參數取值，本身對水文模型具有約束性，水文模型中各個參數具有相對獨立性，因此自動優選法的應用存在一定困難。隨著計算機科學以及人工智能的不斷發展，一些自動尋優算法[7]應用在參數率定中。由于復雜的水文模型的參數個數很多（如SWAT模型有大約200個[8]），使得模型的計算量會隨著參數維度的增加，呈現指數型增長[9]，從而陷入“維數災難”[10]。因此，面對大規模流域模擬，傳統的計算方式已經難以適應當前的計算需求。高性能計算技術的發展使超算領域進入了新的時代。CPU+GPU加速器混合異構架構在高性能計算機中逐漸成為新的發展熱點[11]，如2019年世界超級計算機500強（TOP500）榜首—美國的Summit超算使用的是CPU+GPU混合異構架構。使用高性能異構計算方式來解決工程中遇到的算力匱乏問題已經成為主流，而對于水文模擬參數率定這種具有天然并行性的高計算需求的應用[12]，如何利用異構計算的強大算力解決計算需求，已經成為當前該領域亟待解決的問題之一。在超算平臺上進行水文計算，必須要發展相應的異構算法，高效利用超算平臺的計算資源。本文選取具有較強收斂能力的L-BFGS算法作為基礎率定算法[13]，挖掘其搜索方向及步長的選取原理[14]，在保留算法總體搜索方式的基礎上對其進行并發式改造，使算法具備并發處理多個搜索線路的能力[15]。本文選取適用于中國大多數大江大河及各種流域的HIMS（hydroinformatic modeling system）水文模型[16]作為主要參考模型，通過對模型本身計算熱點的分析，確定適合協處理器計算的部分，并對這一部分進行異構化改造，使得模型的實際運行由CPU端發起，通過各種CPU和協處理器間的數據拷貝，使計算熱點全部運行于協處理器，利用協處理器強大的并發計算能力，在保證計算精度的同時大幅減少計算時間。最后對兩種目前較為常見的異構平臺做了相應的算法測試與對比。

2 并發L-BFGS算法在參數率定中的應用

2.1 水文模型參數率定的評價依據

應用水文模型模擬水文工作時，關鍵的一項就是尋找水文模型的最優參數組，水文模型模擬的精度很大程度上取決于模型中參數組的選擇。參數率定的目標是為待研究流域的各個子流域尋找到一組“最優”的參數組，使得應用該參數組進行水文模擬后的模擬值和實際觀測值的差距最小。通常，參數率定結果的優劣使用Nash（Nash-Suttcliffe，后面簡稱Nash）系數作為判定依據。Nash系數越接近于1，模擬值和觀測值差距越小。Nash系數為

其中，Qo表示觀測值，Qm表示模擬值，Qt表示在第t時刻的某個值。

2.2 L-BFGS算法的并發執行

差商法求導的步驟如下：

將L-BFGS算法所需要的m組初始值、目標函數值和初始值對應的梯度值代入算法中，就可以通過多次迭代找到最優的m個Nash系數。

2.3 HIMS模型的異構移植

HIMS模型是國內自主研發的流域分布式水文模型，具有完全的知識產權。主要應用在流域內評價、規劃和管理水資源，以及處理與水相關的生態環境保護工作[17]，如洪水預報、管理水污染與侵蝕以及氣候變化等。HIMS具有多源信息融合、數字流域分析、分布式模擬以及模型定制等功能[18]，可以針對國內各個流域不同的水文尺度、流域空間非均一性[19]以及不同的自然和人文環境進行水循環模擬、參數率定等水文工作。目前，HIMS模型已應用并部署于國內外眾多流域的水文模擬過程中，并取得了良好的應用效果。

HIMS模型最初是面向CPU端開發，并運行于PC機環境，對于大規模異構計算，需要對HIMS整體架構進行調整。根據目前的協處理器體系結構，原HIMS模型中用于讀取原始數據而開辟的存儲空間需要在計算前全部轉移到device端，并在計算結束后將Nash系數作為結果傳回host端。傳入的數據除原始數據如降雨量、最高最低溫度、海拔、流域面積等，還有已經在host端生成的由m組n維參數組成的數組（x1，1，x1，2，…，x1，n，…，xm，1，xm，2，…，xm，n），并在device端使用線程ID作為標識將參數組分割至m個不同線程。HIMS模型的核心是產流和匯流（即馬斯京根過程）兩大部分，從CPU到協處理器的移植過程包括將涉及的函數定義成device，原始模型中所有的global類型變量、指針全部通過核函數傳入device，模型內部用到的所有變量的內存大小需調整為原先的m倍。計算完之后，使用得到的m組模擬值和實測值通過計算得出m個Nash系數并傳出。圖2和圖3分別為HIMS原始工作流程和HIMS在異構平臺工作流程。

2.4 并發L-BFGS算法的異構實現

并發L-BFGS算法在參數率定中的并發異構實現是通過CPU和GPU協同工作的。首先，CPU同時通過隨機函數產生m組n維參數（x1，1，x1，2，…，x1，n，…，xm，1，xm，2，…，xm，n），將m組n維參數傳入GPU中，按照線程號平均分成m組，每組分別運行HIMS水文模型，得到每組對應的Nash系數，然后將m組參數及其對應的Nash系數取反傳入CPU端，通過差商求導模擬出每組參數每個位置的梯度，將這些變量代入優化算法經過多次迭代，分別判斷每組參數是否達到迭代終止條件，最后得到m個最優參數組和最優Nash系數。L-BFGS算法并發異構實現的基本流程如圖4所示。

3 數值實驗

本節對HIMS模型的異構移植以及并發L-BFGS算法在水文模擬具體參數優化過程進行數值實驗，并比較和分析數值實驗結果，探討異構移植的效率和并發性能以及并發L-BFGS算法在參數率定中的具體應用。運行環境為配置V100的GPU服務器和配置國產AI加速器的國產先進計算平臺，實驗數值均為運行5次計算得出的平均值。

（1） 單節點內國產AI加速器和CPU在參數率定中的并發性能測試。實驗設置參數組個數設置為32 768（1 024×32）、65 536（1 024×64）和13 1072（1 024×128）。由表1，國產AI加速器程序和CPU程序相比，單進程運行時，加速比在125以上，加速效果較為理想，且隨著參數組規模增加，加速比逐漸升高，其中參數組個數從65 536增加到131 072的計算時間從102.59 s增加到202.69 s，說明算例在65 536時基本達到國產AI加速器的滿載狀態，這也與國產AI加速器內含64核、每核支持1 024線程的硬件架構相符。在四進程運行時，保持總參數組數量32 768、65 536、131 072不變，將每進程參數組數量降為原先的四分之一，CPU運行時間約為原先的四分之一，說明強擴展性良好，而國產AI加速器的時間從58.69 s到69.89 s變化不大，說明國產AI加速器的線程還沒有到達計算臨界條件。

從表2中可以看出，在保持每進程以及每個國產AI加速器參數組個數不變時，單進程運行和四進程運行以及單進程1個國產AI加速器和四進程四個國產AI加速器的運行時間相差不大，說明擴展性較好。

（2） L-BFGS算法在串行程序以及異構平臺的國產AI加速器和GPU程序在不同線程Nash系數計算到0.92的迭代次數變化情況。由圖5可知，傳統的L-BFGS算法（即串行實現）在進行參數率定時，迭代次數約在297次Nash系數才能到達0.92，而L-BFGS算法在GPU和國產AI加速器這樣的異構平臺進行多線程并發參數率定時，Nash系數到達0.92的迭代次數隨著線程數增加而逐漸減少。在512線程時只需要迭代大約27次即可使Nash系數到達0.92，說明L-BFGS算法在多線程并發實現較之串行實現時，迭代次數大幅度減少，實現了L-BFGS算法提高率定效率的任務。而在相同線程時，GPU的迭代次數略少于國產AI加速器的迭代次數，說明V100的計算性能略優于當前國產AI加速器的計算性能。

（3） L-BFGS在串行時以及國產AI加速器和GPU在512線程時在不同迭代次數Nash系數變化情況。由圖6，L-BFGS算法在異構平臺的GPU和國產AI加速器實現較之其串行實現在相同迭代次數時，Nash系數要遠大于串行實現，說明，異構運行實現了提高Nash系數精度。而國產AI加速器和GPU在512線程時迭代到200次之后，Nash系數基本保持在0.94左右。

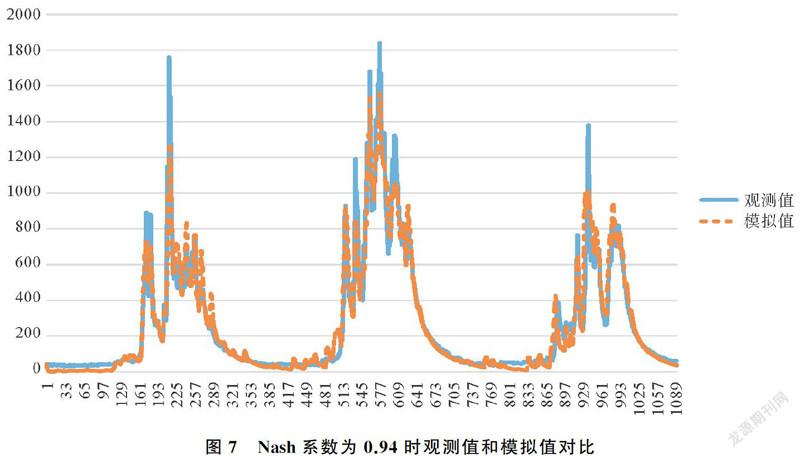
（4） Nash系數為0.94時觀測值和模擬值對比。由圖7，當Nash系數為0.94時，通過水文模擬出來的徑流量模擬值總體趨勢上貼近觀測值，說明通過L-BFGS算法的參數率定使參數集靠近最優參數集，通過這組最優參數集水文模擬出來的徑流量也會與觀測值更加貼近。

4 結論

本文通過對傳統L-BFGS算法進行并發式改進，并將HIMS水文模型進行異構移植，得到了一套面向異構平臺的大規模并發率定算法。針對HIMS模型的參數優化實驗表明，并發L-BFGS算法的異構實現較之串行實現迭代次數有了大幅度減少，且Nash系數的精度也有了較為明顯提高。

參考文獻

[1]劉海帆.基于過程的大尺度水文模型的層級敏感性分析及其在亞馬遜流域中的應用[D].北京：中國地質大學，2020.

[2]QI W， LIU J. Studies on changes in extreme flood peaks resulting from land-use changes need to consider roughness variations[J]. Hydrological Sciences Journal， 2019， 64（16）：2015-2024.

[3]欒承梅.流域水文模型參數優化問題研究[D].南京：河海大學，2005.

[4]郭靖，郭生練，胡安焱，等. 基于TOPSIS法的水文模型多目標參數自動優選方法研究[J].水電能源科學， 2006， 24（6）：25-28.

[5]徐帥帥.基于分布式水文模型的洪水預報及水庫削峰的案例研究[D].濟南：山東建筑大學，2019.

[6]張洪剛，王金星，劉攀，等. 概念性水文模型參數自動優選方法的比較研究[J].石河子大學學報（自然科學版），2002（3）：229-232.

[7]李月玉，李磊，等. 免疫粒子群算法與支持向量機在枯水期月徑流預測中的應用[J].水資源與水工程學報， 2015（3）：124-128.

[8]許自舟， 周旭東， 隋偉娜，等. 基于SWAT模型的碧流河流域入海徑流模擬研究[J]. 海洋環境科學， 2020，39（2）：216-222.

[9]崔東文，鄭斌.幾種智能優化算法與支持向量機相融合的月徑流預測模型及應用[J].人民珠江，2016， 37（3）：18-25.

[10] 馬彥斌，盛旺，李江云，等. 基于遺傳算法的SWMM模型參數率定研究[J].中國農村水利水電，2020（7）：46-49.

[11] 張軍華， 臧勝濤， 單聯瑜，等. 高性能計算的發展現狀及趨勢[J]. 石油地球物理勘探， 2010（06）：918-925.

[12] 高明，程相國，咸鶴群，等.移動端代替算法的并行優化[J].青島大學學報（自然科學版），2016，29（3）：53-58.

[13] CHEN W， WANG Z， ZHOU J. Large-scale L-BFGS using MapReduce[J].Advances in Neural Information Processing Systems， 2014（2）：1332-1340.

[14] KEARSLEY A J. Matrix-free algorithm for the large-scale constrained trust-region subproblem[J]. Optimization Methods &; Software， 2006， 21（2）：233-245.

[15] 于一超，田志遠，劉相靜，等.非線性互補問題的一個數值解法[J].青島大學學報（自然科學版），2014，27（3）：14-18.

[16] 劉昌明，鄭紅星.基于HIMS的水文過程多尺度綜合模擬[J].北京師范大學學報（自然科學 版），2010，46（3）：268-273.

[17] 尚瑞朝，王娟.HIMS系統模型在洪水預報中的應用[J].浙江水利科技，2015，43（4）：9-12.

[18] JIANG Y， LIU C， LI X. Hydrological impacts of climate change simulated by HIMS Models in the Luanhe River Basin， North China[J]. Water Resources Management， 2015， 29（4）：1365-1384.

[19] 吳瀟瀟. HIMS模型在曹江流域流量變化過程模擬中的應用[D].淮南：安徽理工大學，2016.