基于模態分析法的電磁軌道身管緊固仿真優化

李騰達 馮剛 連仲謀

摘 要： 為進一步提升電磁軌道發射器身管緊固的減振優化效果， 采用模態分析法仿真確定緊固點的選取。 在將電磁軌道發射器簡化為伯努利-歐拉梁的基礎上， 進行振動響應分析和模態分析， 通過建立發射器的有限元模型， 模擬發射全過程， 并依據臨界速度時刻的系統剛度進行模態疊加， 確定優化緊固位置并提出評估指標來評判優化效果。 仿真實驗表明， 添加緊固能夠有效提高發射器的剛度， 且緊固的減振效果受到緊固位置的振動特性影響; 緊固的位置選擇應盡量避開臨界速度的共振范圍， 在滿足需求的前提下優先設置位于臨界速度到達位置之前; 添加緊固導致軌道鄰近部位出現應力集中現象， 提高了軌道強度要求。

關鍵詞：電磁發射; 軌道; 減振優化; 模態分析; 有限元仿真

中圖分類號：TJ866??? 文獻標識碼：??? A?? 文章編號：1673-5048（2021）04-0069-07

0 引? 言

電磁發射技術是一項利用電磁力推進負載達到高速的新概念武器技術[1-4]。 在電磁軌道發射器發射過程中， 當電樞速度達到臨界速度時會產生共振， 導致軌道的劇烈振動與撓度變形[5-7]。 由于電磁沖擊力的存在， 軌道的劇烈振動與撓度變形必然會導致軌道的刨削損傷， 影響軌道發射的穩定性與使用壽命[8-9]。 因此在實際應用中， 會對發射器身管施加預緊力以提升結構剛度， 達到減振目的[10]。 針對電磁軌道發射器的振動特性與減振問題， 國內外眾多學者紛紛展開了深入研究。 吳立周等[11]對螺栓緊固封裝進行耦合仿真， 對不同螺栓預緊力下的發射器口徑形變進行了計算， 但忽略了多種影響因素， 如樞軌過盈配合、 速度趨膚效應等; 張永勝等[12]分析了連續發射過程中軌道各成分力的時空分布特性， 但針對軌道振動問題并未提出相應的解決方案; 王振春等[13]提出了通過施加液壓伺服預緊來平衡軌道的振動， 但預緊位置設置時未考慮到軌道瞬態振動響應的影響; 文獻[14]分析了電磁力作用下電樞對軌道的擠壓力和軌道的變形情況; 文獻[15]指出了軌道間的阻尼效應能夠對臨界速度下的軌道撓度變形起到緩解作用; 文獻[16]分析了不同結構剛度和預緊力情況下的軌道振動特性。 這些工作都沒有基于軌道完整瞬態發射過程中的應力載荷空間分布特性進行分析， 勢必會降低研究的計算精度。

本文對電磁軌道發射器完整瞬態發射過程進行了仿真， 依據臨界速度時刻的系統度進行模態疊加分析， 確定了身管緊固的優化位置并提出相應的評價指標。 最后， 對不同緊固位置的優化效果進行對比分析， 提出進一步的身管緊固減振優化方向。

1 軌道動力學分析

1.1 軌道動力學方程

電磁軌道發射器的基礎結構如圖1所示， 其中外圍封裝用于抵消軌道擴張力以維持炮口基本形狀， 彈性支撐用于輔助外圍封裝抵抗軌道變形。

為便于進行動力學理論分析， 將發射器軌道簡化為伯努利-歐拉梁， 如圖2所示。 軌道的動力學方程為

EI4yx4+m2yt2+ky=F（x， t）（1）

式中： E為軌道材料的彈性模量; I為軌道截面的慣性矩; m為軌道線密度， m=ρA， ρ為軌道材料密度， A為軌道截面積; k為彈性支撐剛度;?? F（x，? t）為移動載荷：

F（x，? t）=q（x，? t）[1-H（x-vt）]+f（x，? t）δ（x-vt）（2）

式中： q（x，? t）為軌道間的電磁排斥力; f（x，? t）為電樞對軌道的擠壓力; H為Heviside階躍函數; δ為Dirac脈沖函數。

考慮實際發射過程中的電流趨膚效應， 軌道發射裝置工作原理如圖3所示。

為簡化計算， 假設電流主要集中在趨膚深度中心線位置， 在t時刻， 軌道1中AB段電流在軌道2上任意點p（x1，? -（h+δr）/2）的磁感應強度為

B（x）=μ0i（t）4π[h+δr]1+l-x（l-x1）2+（h+δr）2（3）

則

q（x，? t）=B（x）i（t）（4）

式中： i（t）和δr分別為電流大小和趨膚深度; l， h分別為電樞運動距離和兩軌道間距離; μ0為真空磁導率。

基于彈性力學分析可得， Bernoulli-Euler梁在移動載荷作用下， 當載荷速度接近臨界速度時， 會引起樞軌共振， 導致軌道應力集中急劇增大。 臨界速度表達式為

vcr=44EIkm2（5）

1.2 軌道的固有頻率與振型

對軌道的固有特性進行分析， 令式（1）中F（x，?? t）=0。 其次， 根據分離變量法， 令y（x，?? t）=X（x）T（t）， 代入式（1）可得

T¨（t）T（t）=-EIX（4）（x）+kX（x）mX（x）=-ω2（6）

將式（6）分解為兩個獨立的常微分方程：

T¨（t）+ω2T（t）=0EIX（4）（x）+kX（x）+ω2mX（x）=0 （7）

求解式（7）可得

T（t）=b1cos（ωt）+b2sin（ωt）X（x）=c1cos（βx）+c2sin（βx）+?? c3cosh（βx）+c4sinh（βx） （8）

式中： β=4ω2m-kEI; b1， b2， c1， c2， c3， c4均為待定常數。

由于軌道兩端固定， 則有

X（0）=0， X¨（0）=0X（l）=0，? X¨（l）=0 （9）

可得系統各階固有頻率為

ωn=（nπ）4EI+kl4ml4 （n=1， 2，? 3， …）（10）

相應的固有振型函數為

Xn（x）=sinnπxl（11）

則可將yn（x，? t）表示為

yn（x，? t）=Xn（x）Tn（t）=sinnπxl·（b1ncos（ωnt）+b2nsin（ωnt））（12）

式中： b1n， b2n由初始條件確定。

由于振型函數的正交性， 可將系統位移以振型函數的級數形式表示為

y（x，? t）=∑nXn（x）Tn（t）=∑nsinnπxl·

（b1ncos（ωnt）+b2nsin（ωnt））（13）

1.3 軌道振動的模態分析

模態分析是對模型系統進行動力學分析的方法之一， 研究其振動頻率和振動形式。 對于一個多自由度系統， 其無阻尼振動方程為

My¨+Ky=0（14）

式中： M為結構的質量矩陣; K為結構的剛度矩陣; y¨為加速度矢量; y為位移矢量， 可表示為

y=φsin（ωt）（15）

式中： φ為模態向量; ω為角頻率。

將式（15）代入式（14）， 相應的特征方程為

（K-ω2M）φ=0（16）

式中： φ為非零解， 且滿足系數矩陣行列式為0， 即

det（K-ω2M）=0（17）

令λ=ω2， 則有

det（K-λM）=0（18）

于是， λ的一組特征值可表示為

det（K-λiM）φi=0 （i=1， 2， 3， …，? N）（19）

式中： λi為第i個特征值; φi為第i個模態向量。

在有限元分析中， 剛度矩陣K與質量矩陣M均為實對稱矩陣， 且滿足正交性， 則有

φTiMφj=0，? mi，? ?i≠ji=j（20）

φTiKφj=0，? ki，? ?i≠ji=j（21）

式中： mi為總質量; ki為廣義剛度。

2 有限元模型的建立

電磁軌道發射器身管主要由軌道、 絕緣體、 外圍封裝板、 螺栓預緊件等組成。 圖4～5分別為電磁軌道發射器身管模型和電樞模型。

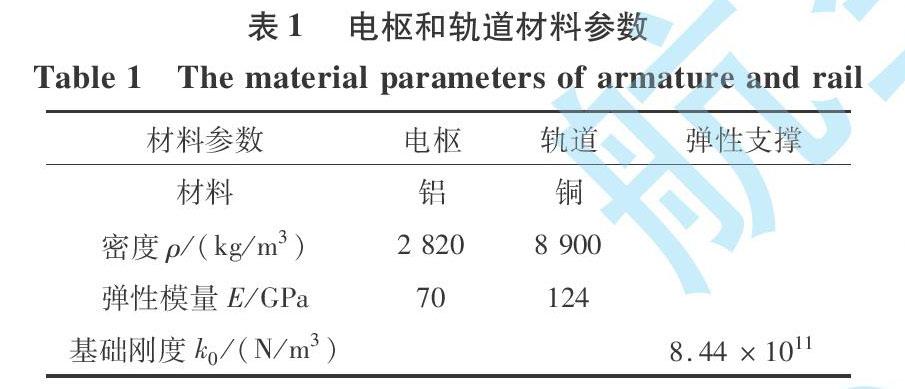
發射器軌道幾何參數為1 000 mm×30 mm×10 mm， 電樞和軌道的材料參數如表1所示， 則軌道的截面慣性矩k為2.5×10-9? m4， 軌道線密度m為2.67 kg/m， 彈性支撐剛度k為2.532×1010 N/m， 可由基礎剛度k0與支撐面面積的乘積求得。? 根據式（5）可得， 軌道的臨界速度為1 448.66 m/s。

為了對電磁軌道發射器的身管緊固進行優化， 在有限元軟件中采用預應力模態分析法， 先進行非線性力學分析， 得到某一關注時刻的系統剛度， 再基于此剛度進行模態分析。 對于電磁軌道發射器這一大型復雜系統， 在電樞達到臨界速度時引起共振， 導致軌道劇烈振動， 是實際工程中需要重點關注的時刻。

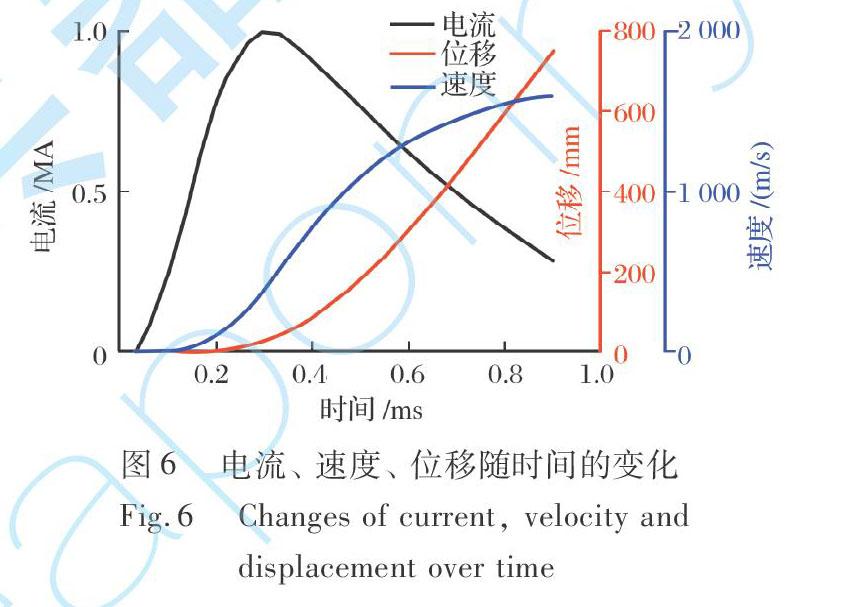
根據上述參數設置， 基于LS-DYNA對電磁軌道發射器進行多場耦合仿真， 考慮電樞運動以及電流趨膚效應， 得到瞬態發射過程中電流、 電樞速度和位移隨時間的變化， 如圖6所示。 由圖6可得， 電樞在 t=0.69 ms時， 距起始端525 mm處， 達到軌道的臨界速度。

3 身管緊固時軌道的振動特性仿真分析

在電磁軌道發射器的發射過程中， 瞬態脈沖電流流過軌道和電樞。 軌道和電樞上的電流密度分布會隨著時間的變化呈現不同的分布特性， 進而影響樞軌受到的電磁力。 圖7為電樞上多個時間點的瞬態電流密度分布。

由圖7可知， 在發射過程初始階段時， 電樞和軌道上的電流密度分布特性隨時間的變化較為劇烈。 在剛通入電流0.01 ms時（圖7（a））， 電流主要分布在軌道與電樞的表面， 同時在電樞臂尾部和電樞喉部均出現較明顯的電流集中現象， 這是由于趨膚效應的影響;? 隨著發射時間增加（圖7（b）～（c））， 電樞由靜止開始加速運動， 電流逐漸滲入軌道與電樞， 尤其是電流在電樞上的分布逐漸變得均勻， 只在電樞喉部依然存在明顯的電流集中;? 在電樞開始運動以后（圖7（d））， 隨著速度的增加， 電樞臂尾部與軌道接觸處， 出現了電流集中， 產生該現象的原因有： （1）電樞臂受到電磁力的影響， 對軌道表面產生了擠壓力， 此處的接觸電阻減小， 電流密度增大; （2）隨著電樞速度的不斷提升， 電樞與軌道電接觸位置出現速度趨膚效應， 速度越大， 趨膚深度越小。

為了分析緊固前后的軌道振動特性變化， 建立電磁軌道發射器的電磁-結構耦合模型， 設定模態求解階數， 求取軌道振動頻率。 在實際工程中， 緊固的減振效果受緊固約束力影響， 且當緊固約束力過小時， 會導致軌道的減振效果降低， 因此將緊固簡化為完全固定約束， 以控制變量便于對比分析。 如圖8所示， 緊固添加在軌道中點， 作用于直徑為20 mm的圓面上。 其中a， b， c為測量點， 分別距起始端250 mm， 375 mm， 625 mm。

圖9為緊固前后軌道上a， b， c三點的撓度隨時間的變化。 相比于無緊固， 有緊固時軌道上三點的振動幅度均有明顯減小， 且振動持續時間有所縮短; 中點緊固對距離較近的b點、 c點的減振效果比a點更明顯。

圖10為緊固前后軌道縱向各處上的最大剪切應力變化。 相比于無緊固， 有緊固時軌道某些位置存在應力突變的現象， 如圖中H點的最大剪切應力為44 MPa， 而該點在無緊固時的最大剪切應力為26.7 MPa。 這可能是由于添加緊固會增大約束部位的預緊力， 從而影響軌道的應力集中水平和發射時的軌道膨脹率， 同時受樞軌耦合振動的影響， 會導致模型部分段產生較大的振幅， 若此處恰好存在約束， 則約束會造成模型出現很大的剪切應力， 進而導致模型損傷。 因此有必要對身管緊固位置進行優化， 使其在起到良好減振效果的同時， 可以盡量避免約束部位產生過大的剪切應力。

4 基于臨界速度時刻的減振優化

在最初無法確定任何一個約束點的位置時， 優化流程是： 先對電磁軌道發射器進行非線性靜力學分析， 再依據臨界速度時刻的軌道剛度進行模態疊加分析， 最后根據模態節點定義約束點。

4.1 基于模態疊加的緊固位置優化

表2為軌道軸向模態前10階振型的參與系數與累加質量因子。 至第10階， 各階有效質量之和近似等于結構總質量， 模態階數足夠。 對各階模態的參與系數進行歸一化， 得到模態疊加系數。

應用Design Assessment模塊進行模態疊加分析， 軌道上下表面的變形如圖11所示。

模態分析中變形值是歸一化后的變形， 用于定性地觀察結構固有振型的共振區域和振動幅度。 很明顯， 可以對圖中區域相對變形小的區域添加緊固約束。 創建基于軌道上下外表面中線的所有節點選擇集， 導出的節點編號及對應的變形經過排序后， 如表3所示。 容易找到節點集內總變形極小值的節點組合分別為： d點（4 700， 21 769）， 總變形量為8.287 4 mm， 距起始端270 mm; e點（3 764， 20 833）， 總變形量為8.426 9 mm， 距起始端660 mm。

4.2 優化效果對比

根據緊固位置的優化方案， 對d點緊固、 e點緊固的減振效果進行仿真對比， 得到優化前后軌道的固有頻率變化（見表4）， 優化前后軌道各點撓度隨時間的變化（見圖12）， 以及優化前后軌道各位置上的最大剪切應力變化（見圖13）。

由表4可得， 優化后軌道的固有頻率要稍小于優化前中點緊固時的固有頻率。 這是由于優化前的緊固位置靠近軌道振動幅度較大處， 緊固較大地增加了模型剛度， 提高了軌道的固有頻率。 為了避免產生過大的剪切應力， 優化位置避開了軌道振幅較大處， 適當提高整個模型的剛度， 同時由于約束點振幅較小， 在相應位置所受的振動沖擊也較小， 較好地提高了整個模型的動力學性能。

由圖12可知， 三種緊固方式均起到良好的減振作用。 相比于中點緊固， d點緊固進一步提高軌道前部的減振效果， 在電樞運動到軌道后部時出現了撓度波動， 表示d點緊固的減振作用受到距離的衰減。 類似地， e點緊固對于軌道后部的減振效果更強， 在軌道前部反而出現了相反效果。 針對這一情況， 可以在已有緊固的基礎上進行模態分析， 再對一個或多個模態節點施加約束， 以達到更好的減振效果。

由圖13可得， 三種緊固方式均在緊固點附近位置出現了應力集中現象。 其中， 緊固點e附近Q點的應力突變最為明顯， 最大剪切應力為100.79 MPa， 在無緊固時為15.7 MPa， 增幅542%。 這是因為在臨界速度工況下， 隨著電樞運動， 軌道撓曲波動逐漸向炮口延伸， 緊固點e正處于軌道劇烈共振范圍， 導致應力集中急劇增大。 同時， 緊固點d附近的P點也產生了應力突變， 最大剪切應力為96.69 MPa， 在無緊固時為63.87 MPa， 增幅51%。 這是由于發射初始階段， 電樞運動加速度大， 導致軌道振動加速度也較大。 相比之下， 軌道中點雖較e點更為接近臨界速度位置， 但采用中點緊固方式時的集中應力只有44 MPa， 可見臨界速度引起的共振對于電樞運動后方的軌道影響較前方小， 因此設置緊固位置時應優先考慮在臨界速度位置之前設置。

綜合分析可得， 身管緊固起到了減振作用， 軌道撓度減小， 彎曲應力減小， 但緊固約束會導致附近軌道上出現應力集中， 使該處的剪切應力有所增大。 對于減振而言， 緊固雖然可能會增大軌道上的剪切應力， 但肯定也會減小軌道因振動產生的屈服應力， 兩者之間存在一個安全裕量， 故需要建立評估指標衡量減振優化后的軌道應力場， 確定減振效果最好的緊固方案。

4.3 評估指標分析

電磁發射器軌道的首要作用是為電樞運動提供平順穩固的發射條件， 以保證良好的發射穩定性， 這就要求軌道具有足夠的剛度、 強度和耐久性。 上文對不同緊固方式的優化效果進行了分析， 不同緊固位置的減振效果受到該處的振動特性限制， 必須合理地選擇， 才能實現預定的減振目標。 如果位置選擇不合理， 導致緊固引起的剪切應力增大， 反而會嚴重影響軌道結構強度。

基于以上考慮， 工程上引入振動傳遞率η， 以便于對比減振前后的效果， 即

η=ahaq（22）

式中： ah為減振后的軌道振動加速度值;? aq為減振前的軌道振動加速度值。

同理， 引入應力變化率γ， 以便于對比減振前后軌道強度變化， 即

γ=τh-τqτq（23）

式中： τh為減振后的軌道最大剪切應力值; τq為減振前的軌道最大剪切應力值。

表5為不同緊固方式下優化前后的軌道最大振動加速度值與傳遞率。? 由表5可得， d點緊固時軌道各測量點的傳遞率均小于10%， 可見其對于軌道各個位置均有良好的減振效果; 相比于d點緊固， 中點緊固對軌道后部的減振效果更好， 但對軌道前部的減振效果較差， 對整個結構的減振作用不夠全面; 而e點緊固的減振效果最差， 僅對軌道末端的減振效果比較明顯。

表6為不同緊固方式下優化前后的軌道最大剪切應力值與應力變化率。

由表6可得， d點緊固位置處減震前的最大剪切應力的變化率也是最小的， 其對軌道強度的要求最低。

因此， 綜合考慮緊固的減振效果與應力集中負效應， 可認為基于該仿真模型的d點緊固方式為最優減振方案。

5 結? 論

針對電磁軌道發射器瞬態發射過程中的振動問題， 對身管緊固的減振效果進行優化。 基于電磁軌道發射器臨界速度時刻的系統剛度進行模態分析， 提出減振優化方法， 對不同緊固位置的減振效果進行對比分析， 得出以下結論：

（1） 緊固的減振效果受到緊固位置的振動特性影響， 包括原始振動幅度、 振動頻率等。 同時， 因受外界激勵和樞軌耦合振動影響， 軌道上的緊固約束會導致大剪切應力， 進而引起損傷。 減振優化時應綜合考慮軌道強度、 剛度要求， 選擇合適位置添加緊固， 以適當提高軌道強度要求， 減弱振動影響。

（2） 單點緊固已達到了良好的減振效果。 對于減振效果的遠端弱化問題， 可以嘗試在已有緊固的基礎上進行二次模態疊加， 確定多個模態節點施加約束， 以達到更好的減振效果。

（3） 發射過程中軌道前段的振動幅度大， 緊固軌道前段的減振效果較為明顯; 緊固軌道后段時， 應避開臨界速度效應的影響范圍， 且由于軌道撓曲波動逐漸向炮口延伸， 緊固設置于臨界速度位置之前為佳。

參考文獻：

[1] Vertelis V，? Vincent G，? Schneider M，? et al. Magnetic Field Expulsion from a Conducting Projectile in a Pulsed Serial Augmented Railgun[J]. IEEE Transactions on Plasma Science，? 2020，? 48（3）：? 727-732.

[2] 馬偉明，? 魯軍勇. 電磁發射技術[J]. 國防科技大學學報，? 2016，? 38（6）：? 1-5.

Ma Weiming，? Lu Junyong. Electromagnetic Launch Technology[J]. Journal of National University of Defense Technology，? 2016，? 38（6）：? 1-5.（in Chinese）

[3] Lin Q H，? Li B M. Numerical Simulation of Interior Ballistic Process of Railgun Based on the Multi-Field Coupled Model[J]. Defence Technology，? 2016，? 12（2）：? 101-105.

[4] 李軍，? 嚴萍，? 袁偉群. 電磁軌道炮發射技術的發展與現狀[J]. 高電壓技術，? 2014，? 40（4）：? 1052-1064.

Li Jun，? Yan Ping，? Yuan Weiqun. Electromagnetic Gun Technology and Its Development[J]. High Voltage Engineering，? 2014，? 40（4）：? 1052-1064.（in Chinese）

[5] 吳金國. 電磁軌道炮樞軌結構動力學與超高速刨削研究[D]. 南京：? 南京理工大學，? 2018.

Wu Jinguo. Study on the Armature-Rail Structure Dynamics and Hypervelocity Gouging of Electromagnetic Railgun[D]. Nanjing：? Nanjing University of Science and Technology，? 2018. （in Chinese）

[6] 吳金國，? 林慶華，? 栗保明. 電磁軌道發射裝置導軌動力學響應分析[J]. 振動工程學報，? 2019，? 32（1）：? 120-127.

Wu Jinguo，? Lin Qinghua，? Li Baoming. Dynamic Response Analysis of Conducting Rails in Electromagnetic Rail Launcher[J]. Journal of Vibration Engineering，? 2019，? 32（1）：? 120-127. （in Chinese）

[7] Lee Y H，? Kim S H，? An S，? et al. Dynamic Response of an Electromagnetic Launcher Accelerating a C-Shaped Armature[J]. IEEE Transactions on Plasma Science，? 2017，? 45（7）：? 1639-1643.

[8] Lu J Y，? Du P P，? Feng J H，? et al. Simulation Study on Critical Velocity of Electromagnetic Rail Launcher[C]∥Proceedings of the CSEE，? 2019，? 39（7）：? 1862-1870.

[9] Mrsnik M，? Slavic J，? Boltear M，? et al. Vibration Fatigue Using Modal Decomposition[J]. Mechanical Systems and Signal Processing，? 2018：? 548-556.

[10] 姜遠志， 魯軍勇， 吳海， 等.軌道式電磁發射裝置外加固層的力學分析[J].海軍工程大學學報， 2019， 31（6）： 34-39.

Jiang Yuanzhi，? Lu Junyong，? Wu Hai，? et al. Mechanical Analysis of Outer Reinforcement Layer of Orbital Electromagnetic Launchings [J]. Journal of Naval University of Engineering，? 2019，? 31（6）： 34-39. （in Chinese）

[11] 吳立周，? 古剛，? 耿昊，? 等. 螺栓緊固型軌道發射器預緊力[J]. 強激光與粒子束，? 2015，? 27（4）：? 045005.

Wu Lizhou，? Gu Gang，? Geng Hao，? et al. Pre-Compression of Bolton Rail-Launcher[J]. High Power Laser and Particle Beams，? 2015， 27（4）：? 045005. （in Chinese）

[12] 張永勝，? 魯軍勇，? 譚賽，? 等. 連續電磁發射過程中軌道受力分析[J]. 兵工學報，? 2018，? 39（3）：? 618-624.

Zhang Yongsheng，? Lu Junyong，? Tan Sai， ?et al. Analysis of Force Load on the Rail in Rapid-Fire Mode of Electromagnetic Rail Launcher[J]. Acta Armamentarii，? 2018，? 39（3）：? 618-624. （in Chinese）

[13] 王振春，? 楊德功，? 張玉燕. 液壓伺服預緊的電磁發射軌道振動頻率和幅值特性研究[J]. 兵工學報，? 2019，? 40（1）：? 29-34.

Wang Zhenchun，? Yang Degong，? Zhang Yuyan. Research on Vibrational Frequency and Amplitude Characteristics of Electromagnetic Launch Rail under Hydraulic Pre-Load[J]. Acta Armamentarii，? 2019，? 40（1）：? 29-34. （in Chinese）

[14] 崔孟陽，? 王學智，? 丁日顯，? 等. 軌道炮發射過程中軌道的受力與變形問題研究[J]. 彈箭與制導學報，? 2019，? 39（4）：? 114-117.

Cui Mengyang，? Wang Xuezhi，? Ding Rixian，? et al. Study on Stress and Deformation of Rails during Launching Process of Railgun[J]. Journal of Projectiles，? Rockets，? Missiles and Guidance，? 2019，? 39（4）：? 114-117. （in Chinese）

[15] Lewis K B，? Nechitailo N V. Transient Resonance in Hypervelocity Launchers at Critical Velocities[C]∥IEEE Transactions on Magnetics，? 2007：? 157-162.

[16] Che Y L，? Yuan W Q，? Xu W D，? et al. The Influence of Different Constraints and Pretightening Force on Vibration and Stiffness in Railgun[J]. IEEE Transactions on Plasma Science，? 2017，? 45（7）：? 1154-1160.

Simulation Optimization of Body Tube Fastening of

Electromagnetic Rail Based on Modal Analysis

Li Tengda，? Feng Gang ，? Lian Zhongmou

（Air Force Engineering University，? Xian 710051，? China）

Abstract：? In order to further improve the vibration reduction optimization effect? of the electromagnetic rail transmitter body tube fastening，? the modal analysis method is used to simulate the selection scheme of? fastening point. On the basis of simplifying the electromagnetic orbit emitter into Bernoulli-Euler beam，? the vibration response analysis and modal analysis are carried out，? and the whole process of emission is simulated by establishing the finite element model of the transmitter. According to the system stiffness of critical velocity，? the optimal fastening position is determined and the evaluation index is put forward to evaluate the optimization effect. The simulation results show that the addition of fastening can effectively improve the stiffness of the transmitter， and the vibration absorption effect of the fastening is affected by the vibration characteristics of the fastening position，? and the selection of the fastening position should avoid the resonance range of the critical velocity as far as possible， and the position is located before the arrival position of? the critical speed on the premise of meeting the requirements，? the addition of fastening leads to the stress concentration in the adjacent parts of the rail to improve the rail strength.

Key words：? electromagnetic launch; rail; vibration reduction optimization; modal analysis; finite element simulation