裝配式公路橋梁抗震分析與驗算
李子特 王根會

摘? 要:以高速公路中典型的裝配式混凝土橋梁下部結構為分析及驗算對象,選取代表性的15m墩高及25m墩高構造及配筋設計和支座設置情況,采用反應譜法進行了抗震分析及驗算。其中,利用彈性屈曲分析方法求解了橋墩端部不同約束條件下順橋向和橫橋向的計算長度,利用靜力彈塑性poshover分析方法求解了框架橋墩橫橋向的極限位移。計算結果表明:在E1地震作用下,橋墩處于彈性階段,承載力有較大富余;在E2地震作用下,15m、25m橋墩柱間系梁及墩底截面進入彈塑性變形階段,形成了塑性鉸;對塑性鉸區域內箍筋進行加密設置,其抗剪承載力及墩頂位移滿足現行規范要求。為同類橋梁抗震分析及驗算提供借鑒和參考。
關鍵詞:計算長度;抗震;反應譜;彈塑性;塑性鉸
中圖分類號:U4? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼:A
0? 引言
裝配式橋梁由于可采用標準化預制、縮短施工周期、便于控制施工質量等多種優點,是公路工程中應用最為廣泛的結構形式[1]。在地震作用下,一聯內橋墩根據自身剛度不同,能夠形成與之協同的抗震體系,這樣的受力是最有利和經濟的。在高震區,橋墩構造及配筋設計、支座選型一般均由地震作用控制[2]。對應不同的墩高,需要通過支座剛度結組合后調整墩相對剛度。在現行規范和產品體系下,對于雙柱式輕型橋墩,一般形成了10m以下墩高采用高阻尼支座、10~25m墩高采用水平力分散性支座、25~35m墩高采用盆式支座墩梁固結的形式,其實質是調整了橋墩端部的約束剛度,從而調整了橋墩作為壓彎構件的計算長度。根據《公路橋梁抗震設計規范JTG/T 2231-01-2020》,規則橋梁采用反應譜法進行抗震驗算。以5×30m一聯、墩高25m以下柱式橋墩采用水平力分散性橡膠支座、墩高25m以上柱式橋墩采用固定盆式橡膠支座的典型橋聯,對E1地震作用下橋墩彈性強度及E2地震作用下橋墩彈塑性強度、位移能力、抗剪強度進行驗算。
1? 工程概況
某高速公路項目,上部結構采用部頒30m裝配式預應力混凝土連續箱梁通用圖,下部結構采用柱式墩、柱式臺配鉆孔灌注樁基礎,橋寬12.5m。取典型5×30m一聯進行計算,1、4號橋墩高度取15m (不含蓋梁),1.6m柱徑配1.8m樁基,墩柱間距為6.8m,設置1道地系梁、1道柱間系梁,采用LNR-d420×128水平力分散型橡膠支座;2、3號橋墩高度取25m (不含蓋梁),1.8m柱徑配2.0m樁基,墩柱間距為6.8m,設置1道地系梁、1道柱間系梁,采用JPZ(Ⅱ)1.5GD盆式橡膠支座;橋臺樁間距為6.8m,樁徑為1.6m,采用GYZF4300x65型四氟滑板式橡膠支座。地震動峰值加速度為0.15g 相當于地震基本烈度Ⅶ度,B類橋梁提高一級按照Ⅷ級設防,分區特征周期0.45s。
橋梁上下部結構之間采用支座連接,其彈性連接剛度如下表:
樁基主筋是橋墩主筋根數的1.5倍,塑性鉸區域箍筋雙繞,為非塑性鉸區域的2倍,橋墩及樁基的截面配筋及體積配箍情況如下表所示。
2? 計算模型建立
采用MIDAS/CIVIL 2020建立空間有限元計算模型,箱梁、蓋梁、墩柱、樁基等均采用空間梁單元模擬,樁與土相互作用采用地基土彈簧進行模擬[3],彈簧剛度計算按照《公路橋涵地基與基礎設計規范》中地基土的比例系數m 進行簡化。本橋上覆層為黃土,下覆層為泥巖取值,6m以上土彈簧剛度取為8000kN/m4,6m以下取為25000kn/m4,地震作用采用反應譜加載。
混凝土梁橋反應譜分析取固定阻尼比為0.05,荷載組合采用偶然組合。
3? 墩柱計算長度
地震作用下,橋墩受力類型為壓彎構件,計算承載力時需要根據橋墩端部的實際約束剛度求解其計算長度[4]。建立有限元模型,通過對15m橋墩、25m橋墩蓋梁中心施加豎向單位力,進行屈曲分析,求得順橋向和橫橋向的穩定系數,再通過歐拉臨界公式,求解計算長度系數。
從上表可以看出,橋墩順橋向力學計算模型類似于墩底固結、墩頂自由的壓彎構件;橋墩橫橋向由于墩柱的框架效應,其力學計算模型類似于墩底固結、墩頂彈性連接的壓彎構件。
4.? E1地震作用驗算
無論從地震病害調查分析,還是地震反應計算,雙柱式橋墩順橋向潛在塑性鉸在墩底處,橫橋向潛在塑性鉸位置在墩頂、墩底及柱系梁截面處[5],對其位置處進行控制性驗算。
從上表計算結果可以看出,在E1地震作用下,墩柱均處于彈性受力階段,且承載力有較大富余。
5 E2地震作用計算
在E2地震作用下,首先進行承載能力計算,判斷橋墩潛在塑性鉸位置處截面是否屈服。如果屈服,即潛在塑性鉸區域截面處已進入彈塑性變形階段,此時需要進一步驗算塑性鉸的位移延性能力及抗剪承載力作為能力保護構件驗算[6]。
5.1橋墩彈性強度驗算
取墩頂、墩底及柱間系梁截面潛在塑性鉸位置進行控制性驗算。
從上表可以看出,在E2地震工況下,15m、25m橋墩柱間系梁及墩底截面偏心受壓類型強度超過彈性極限,該部位已進入塑性變形階段,即形成了塑性彎曲鉸。
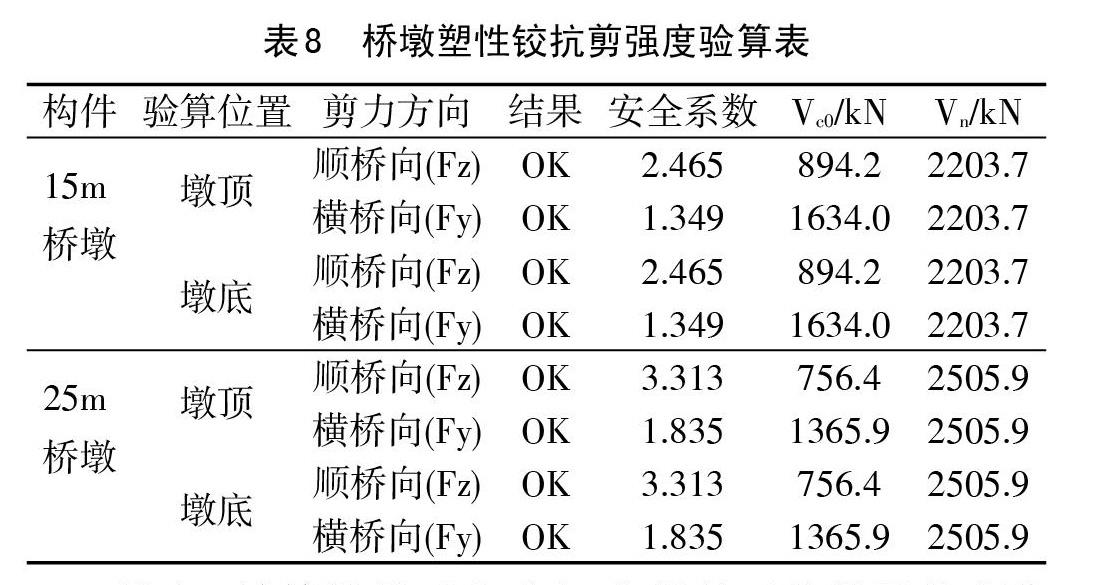
5.2橋墩塑性鉸抗剪強度驗算
E2彈塑性地震作用下,墩柱塑性鉸區域抗剪承載力作為能力保護設計[7],依據《抗規》相關內容進行計算。
從上表計算結果可以看出,塑性鉸區抗剪承載力滿足規范要求。
5.3橋墩墩頂位移驗算
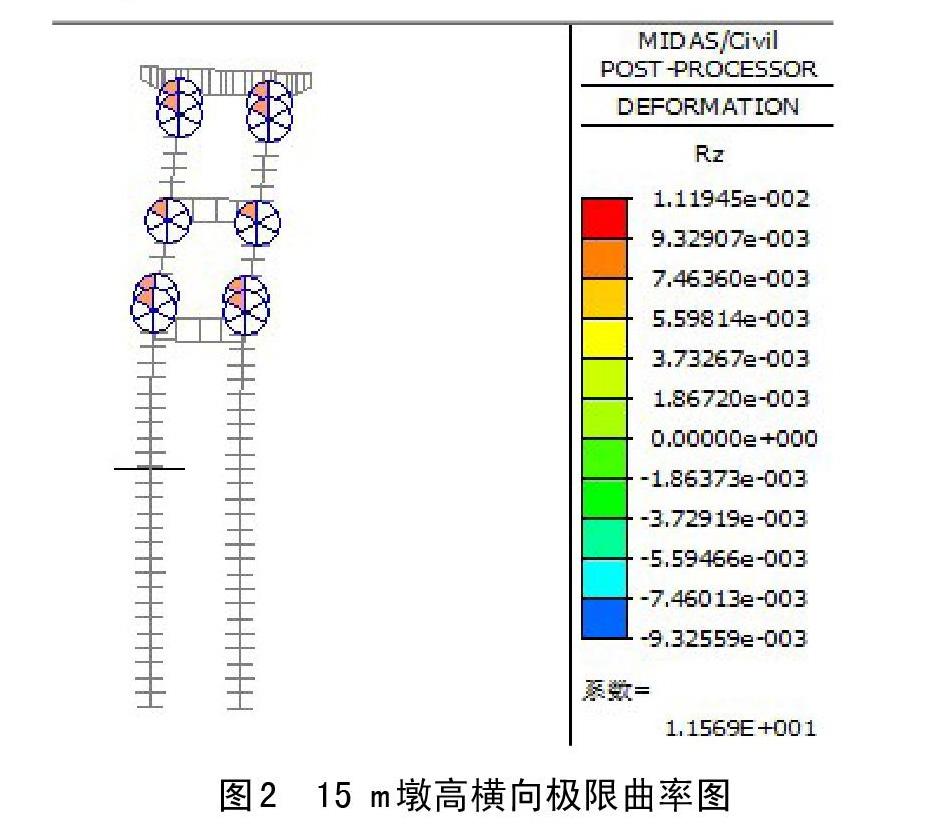
在E2地震作用下,規則橋梁橋墩墩頂位移應小于其允許值。其中,橋墩順橋向允許位移按《抗規》相關內容進行計算。雙柱式框橋墩橫橋向允許位移利用靜力彈塑性分析方法進行求解[7],即采用MIDAS/CIVIL中pushuover功能進行求解。
從上表計算結果可以看出,在E2地震作用下墩頂順橋向和橫橋向位移均小于橋墩容許位移,滿足規范要求。
6? 結論
(1)橋墩順橋向力學計算模型類似于墩底固結、墩頂自由的壓彎構件;橋墩橫橋向由于墩柱的框架效應,其力學計算模型類似于墩底固結、墩頂彈性連接的壓彎構件。
(2)在E1地震作用下橋墩處于彈性階段。
(3)在E2地震作用下,15m、25m橋墩柱間系梁及墩底截面進入彈塑性變形階段,形成了塑性鉸。
(4)塑性鉸區的抗剪承載力及塑性位移能力滿足規范要求。橋墩構造及配筋設計、支座選型方案是合理可行的。
參考文獻
[1]汪泉清.高烈度區裝配式公路橋梁抗震性能研究[J].中外公路,2020,12,132-135
[2]馬潤平,高延奎.高烈度區預制橋梁支座的選取[J].公路交通科技,2020,04,170-172.
[3]王立軍.軸心受壓桿件的彎曲屈曲[J].建筑結構,2017,10,126-135
[4]胡銳光,何敏,鄭宗平,王昭陽.樁土作用對連續梁橋抗震性能的影響分析[J].公路工程,2017,01,76-79
[5]王濟源, 李雪婷.橋梁震害及抗震設計方案[J].工程建設與設計, 2020,03,123-125.
[6]郭凱斌,溫泉.提高公路橋梁抗震能力的措施[J].交通世界,2019,11,126-127
[7]中華人民共和國交通運輸部,公路橋梁抗震設計規范JTG/T 2231-01-2020 [S].北京:人民交通出版社, 2020

