改進雙向蟻群算法的移動機器人路徑規劃

李二超，齊款款

蘭州理工大學 電氣工程與信息工程學院，蘭州730050

靜態環境下的移動機器人路徑規劃是指在已知環境中，按照一定的算法，根據目標函數（如距離最短等），尋找一條從起點到終點的安全且最優路徑[1]。

二維靜態環境下機器人路徑規劃算法有很多，如A*算法、遺傳算法、粒子群算法和蟻群算法，其中，A*算法速度快但轉折點較多，隨著環境復雜度的增加，搜索代價呈指數增長[2]，遺傳算法在種群初始化、算法迭代等環節代價函數建模困難，路徑搜索效率低，耗費較大的計算和存儲資源，在復雜環境下的路徑規劃效率低下，需要較長時間才能規劃出可行路徑，且路徑并非最短[3]，粒子群算法簡單易行，通用性強，但在算法初期局部搜索能力較差，后期易陷入局部最優等[4]，而選擇蟻群算法的原因是，蟻群算法是一種啟發式的隨機搜索算法，該算法由模擬自然界螞蟻行為而來，并通過信息素的積累產生的正向反饋來尋找最優路徑，隨著環境復雜度的增加，路徑搜索代價不會指數增長，且具有較強的魯棒性，優良的并行分布式計算能力、無中心控制、易于與其他算法融合的優點[5-6]，但無法找到最短路徑，收斂速度慢，路徑搜索盲目性大、且路徑拐點較多。針對以上蟻群算法的缺陷，不同的學者有著各自的改進方法。張蘇英等人[7]采用雙向蟻群算法，但并未使用相遇條件，即起點螞蟻搜索路徑完成后，終點螞蟻才開始進行路徑搜索，雖然能提高全局搜索能力，但并不能縮減算法運行時間。文獻[8]采用初始信息素不平等分布的同時，在啟發函數中引入轉角因子，能夠較快得到拐點較少的最優路徑。王紅君等人[9]使用冗余點的刪除策略，能夠減少路徑上的拐點數目。陳英俏[10]采用信息素非均勻分布的并行雙向蟻群算法，相遇條件為信息素相遇，即在同一柵格出現雙向不同的信息素視為相遇，同時在啟發函數中引入信息素相互引導策略，加強了信息素作用，減少了算法運行時間。Luo等人[11]使用偽隨機概率轉移公式提高了算法的全局搜索能力和收斂速度。徐義晗等人[12]采用建立方向信息素矩陣的雙向蟻群算法，能夠提高路徑搜索速度和路徑的多樣性。王曉燕等人[13]利用人工勢場法求得的初始路徑信息對蟻群算法的啟發函數進行改進，增強路徑的引導作用，減小路徑搜索的盲目性。文獻[14]采用雙向蟻群算法路徑搜索策略，能夠加快算法運行速度和提高全局搜索能力，但仍然是一小步的搜索，路徑轉折點依然較多。文獻[15]通過改進信息素增強系數，信息素揮發因子，建立信息素因子和啟發式因子的互鎖關系，減少了算法的迭代次數，提高了算法的收斂速度。本文算法與雙向蟻群算法（如文獻[14]）相比，優勢在于減少路徑搜索的節點數（有效頂點數少于環境總柵格數），打破傳統總是一小步的路徑搜索方式以及轉移角度45?整數倍的限制，動態調節揮發系數，得到的路徑拐點較少，路徑更短。

傳統蟻群算法存在很多的缺陷，針對傳統蟻群算法無法找到最短路徑，路徑搜索盲目性大，收斂速度慢，拐點多問題，提出基于改進雙向蟻群算法的機器人路徑規劃。首先，改進路徑搜索方式，即基于障礙物有效頂點編碼的路徑搜索，不再使用傳統的從當前柵格中心到下一柵格中心一步步的路徑搜索，而是從當前障礙物有效頂點到下一可選障礙物有效頂點的大步的路徑搜索，結合雙向蟻群算法路徑搜索策略，能夠加快收斂速度且能夠找到拐點相對更少的最短路徑。其次，由于采用障礙物有效頂點編碼的路徑搜索，啟發式函數也隨之做了改進，即當前障礙物有效頂點到下一可選障礙物有效頂點的歐氏距離的倒數，并在公式分母中加入調節參數，有助于找到更短路徑。同時，引入偽隨機（隨機概率和任一性概率）的狀態轉移策略，能夠降低傳統算法路徑搜索的盲目性。最后，為防止信息素積累過多，自適應調節信息素揮發系數的同時，設置信息素濃度的取值范圍。

1 環境建模

機器人工作環境為靜態柵格地圖，如圖1所示。黑色柵格代表障礙物，用1表示，白色柵格代表自由柵格，用0表示。地圖按照從左到右，從下到上的順序依次編號1、2、…，柵格序號與坐標一一對應，坐標與柵格編號的關系表達式如式（1）：

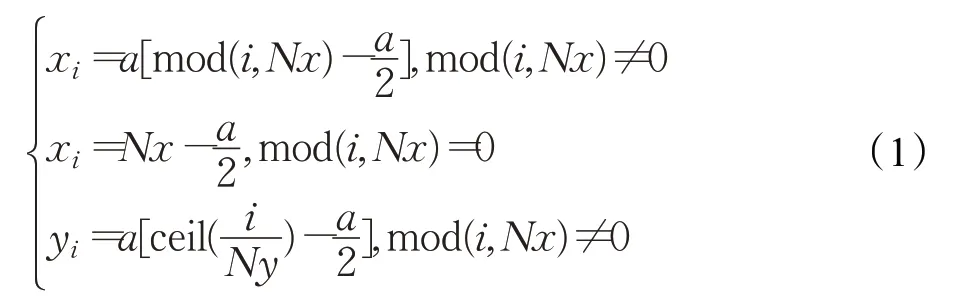
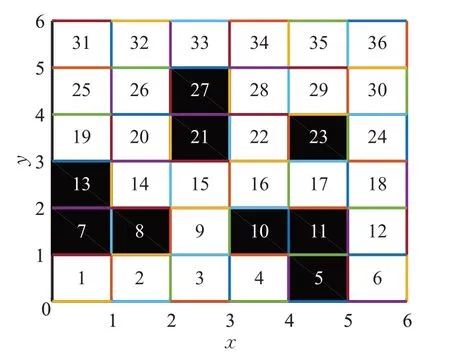
圖1 柵格地圖Fig.1 Grid map

其中，i代表柵格序號，Nx柵格地圖的行數，Ny柵格地圖的列數，mod是求余運算，ceil是向上取整運算。

將障礙物進行膨化處理，如圖2所示。最里面黑色正方形為原始障礙物，當不規則障礙物不滿一個柵格時，將其填充為一個柵格，白色部分為障礙物的膨化，寬度為機器人半徑，最外層黑色部分為安全距離，整體構成障礙物，此時把機器人看作質點來處理，假設膨化后的正方形邊長為1，即式（1）中的a=1。本文研究的目標為路徑最短。

圖2 障礙物膨化處理Fig.2 Expansion treatment of obstacles

2 傳統蟻群算法

狀態轉移概率公式如式（2）所示：

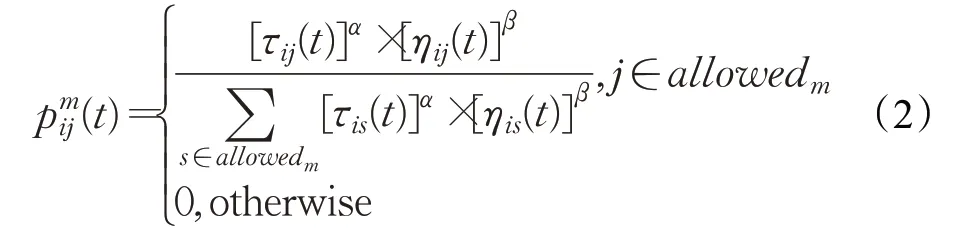
式中，j∈allowedm為待選節點集合；τij(t)為信息素濃度；ηij(t)為啟發信息，用當前節點i到下一節點j的歐式距離的倒數表示；α和β分別表示信息素因子和啟發式因子。

信息素更新公式如式（3）~式（5）所示：

式中，τij(t+1)為更新后的信息素濃度；ρ為信息素揮發系數；Δτij(t)為所有螞蟻信息素濃度之和；Q為信息素強度；Lm為螞蟻所走的路徑長度。

3 改進蟻群算法

3.1 障礙物有效頂點

障礙物有效頂點定義及條件：

（1）柵格地圖最外圍邊界上的所有點都不可能成為障礙物的有效頂點。

（2）由當前小柵格與相鄰的三個小柵格組成的“田”字形中，當且僅當只有一個障礙物時，田字格的中心點為障礙物的有效頂點。

必須同時滿足以上條件才能成為障礙物的有效頂點。例如在圖3中柵格13、14、19和20四個小柵格組成“田”字形較大柵格9個點中，點（0，2）、（0，3）和（0，4）為柵格地圖最外圍邊界上的點，不滿足條件（1），不是障礙物的有效頂點，分別以點（1，2）、（1，4）和（2，4）為中心的田字格中分別有3個障礙物、無障礙物和2個障礙物，不滿足條件（2），不是障礙物的有效頂點，點（1，3）、（2，2）和（2，3）滿足上述的兩個條件，故為障礙物的有效頂點。圖3中有14個障礙物有效頂點，用紅色的五角星表示，紅色三角形分別為起點（S）和終點（E），定義為廣義的障礙物有效頂點（起點和終點分別是有效頂點連接路徑的首端和末端），因此圖中共有16個有效頂點。

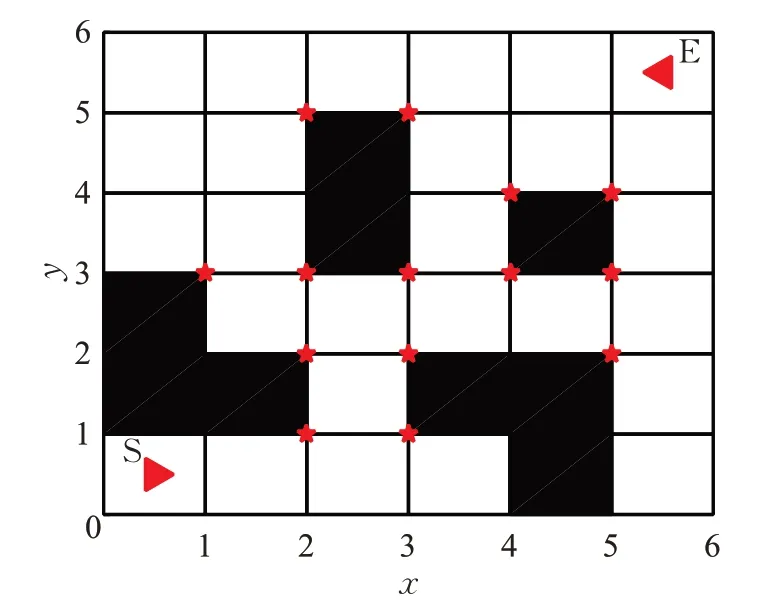
圖3 障礙物有效頂點示意圖Fig.3 Diagram of effective vertex of obstacles

基于障礙物有效頂點的路徑搜索需要對每個有效頂點進行編碼，以便于路徑的識別和搜索，從下向上，從左向右依次進行編號（起點和終點編號為1和2除外），例如圖3中的16個有效頂點，以先后順序從1編號到16，順序為S→E→（1，3）→（2，1）→（2，2）→（2，3）→（2，5）→（3，1）→（3，2）→（3，3）→（3，5）→（4，3）→（4，4）→（5，2）→（5，3）→（5，4）。

3.2 改進雙向搜索策略

雙向蟻群算法路徑相遇條件不同于文獻[14]信息素相遇條件，即有效頂點相遇條件，具體如圖4所示。

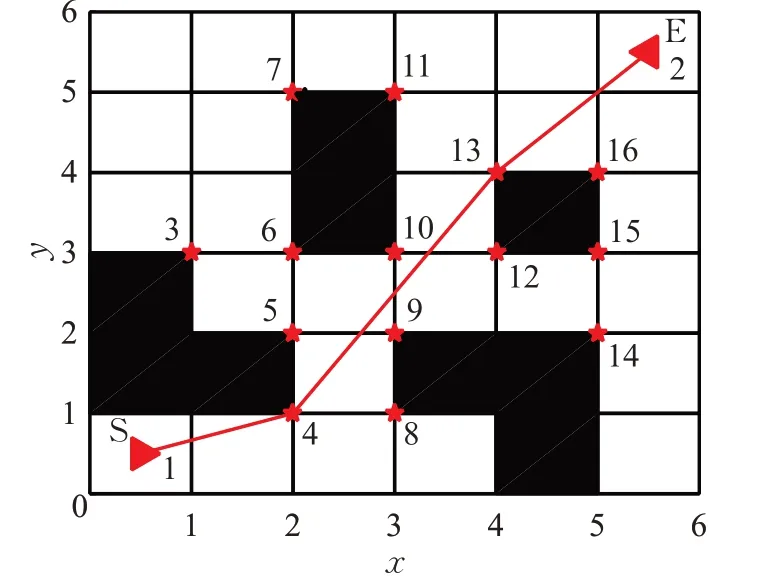
圖4 障礙物有效頂點路徑規劃仿真示意圖Fig.4 Simulation diagram of effective vertex path planning of obstacles

螞蟻平均分成兩組，一組放在起點位置，從起始點（S）向目標點（E）進行搜索（正向搜索），一組放在目標點位置，從目標點向起始點進行搜索（反向搜索），采用輪流交替從兩個方向進行搜索，即先從起點派出一只螞蟻向目標點進行一步路徑搜索（此時的一步并非傳統算法的一小步，有可能是多步），然后從目標點派出一只螞蟻向起點進行一步路徑搜索。

當正向搜索一步后，判斷與反向搜索的路徑有無相同有效頂點，若有，則結束搜索，若沒有，則從目標點派出一只螞蟻向起點進行一步路徑搜索，判斷與正向搜索的路徑有無相同有效頂點，若有，則結束搜索，若沒有，則從起點派出一只螞蟻向終點進行一步路徑搜索，再進行判斷有無相同的有效頂點，如此反復進行，直到相遇在相同的有效頂點然后從相同的有效頂點分別向起點和終點回溯，形成一條完整的路徑并記錄。

圖4為某兩只螞蟻路徑搜索仿真示意圖，起點和終點分別編號為1和2，分別加入到road0和road1路徑集合中。有一只正向搜索的螞蟻在起點，根據有效頂點的鄰接矩陣可知，下一步有2個可選的有效頂點4和8，再根據狀態轉移規則，選擇有效頂點4，并加入road0集合（此時集合中有1和4兩個元素），判斷與反向路徑無相同的有效頂點，此時反向搜索的螞蟻從終點出發，根據有效頂點的鄰接矩陣，下一步有8個可選的有效頂點5、7、10、11、13、14、15和16，再根據狀態轉移規則，選擇有效頂點13，并加入road1集合（此時集合中有2和13兩個元素），判斷與正向路徑無相同的有效頂點，此時執行正向的路徑搜索，根據有效頂點的鄰接矩陣，下一步有8個可選的有效頂點5、6、7、8、9、10、12和13，再根據狀態轉移規則，選擇有效頂點9，并加入road0集合。判斷與反向路徑無相同的有效頂點，此時反向搜索的螞蟻從終點出發，根據有效頂點的鄰接矩陣，下一步有7個可選的有效頂點4、5、9、10、11、12和16，選擇有效頂點4，并加入road1集合，判斷與正向路徑有相同的有效頂點4，則結束搜索，此時road0：S→4→9，road1：E→13→4，最終路徑roadlast：S→4→13→E（具體編號規則見上文）。

3.3 改進轉移概率公式

改進的啟發函數如式（6）所示：

式中，dij表示當前有效頂點與下一有效頂點之間的歐氏距離。a,b為正數。roadxij表示正向或反向搜索，其中x=0,表示正向搜索，x=1,表示反向搜索。

啟發函數的改進，相應的轉移概率也跟著改變，并引入任一性概率。具體改進轉移概率公式如式（7）、（8）所示：

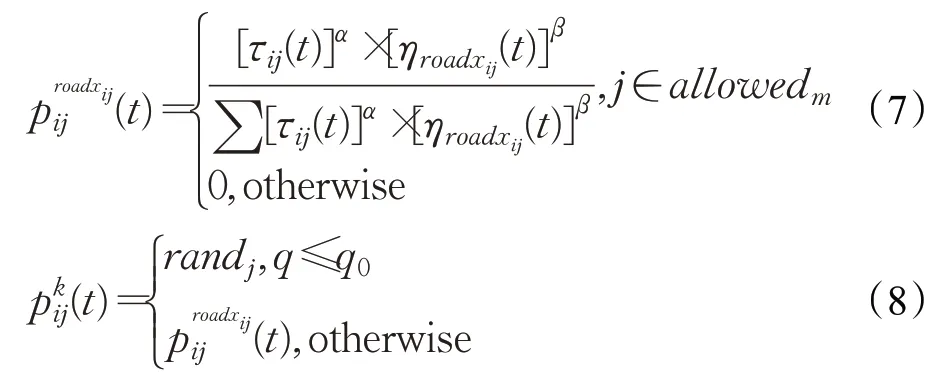
式中，q為[0，1]之間的隨機數，q0由反復實驗來確定的常數，范圍為（0，1），randj為在可選有效頂點中任選其一。

3.4 改進揮發系數

改進的揮發系數能夠實現動態調節，如式（9）所示：

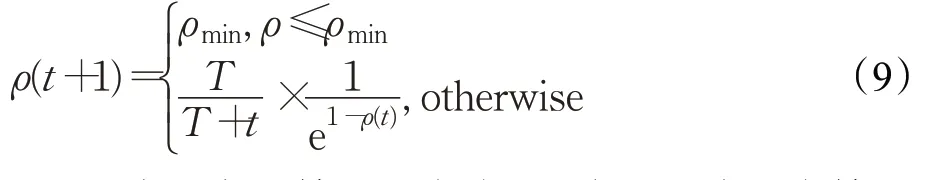
式中，ρmin為揮發系數的最小值，T為最大迭代次數，t為當前迭代次數。

3.5 信息素限制策略

為防止算法陷入局部收斂，對信息素濃度進行限制，信息素大小限制范圍如式（10）所示：

式中，τmin為信息素最小值，τmax為信息素最大值。

4 改進蟻群算法流程

改進后的蟻群算法流程圖如圖5所示。

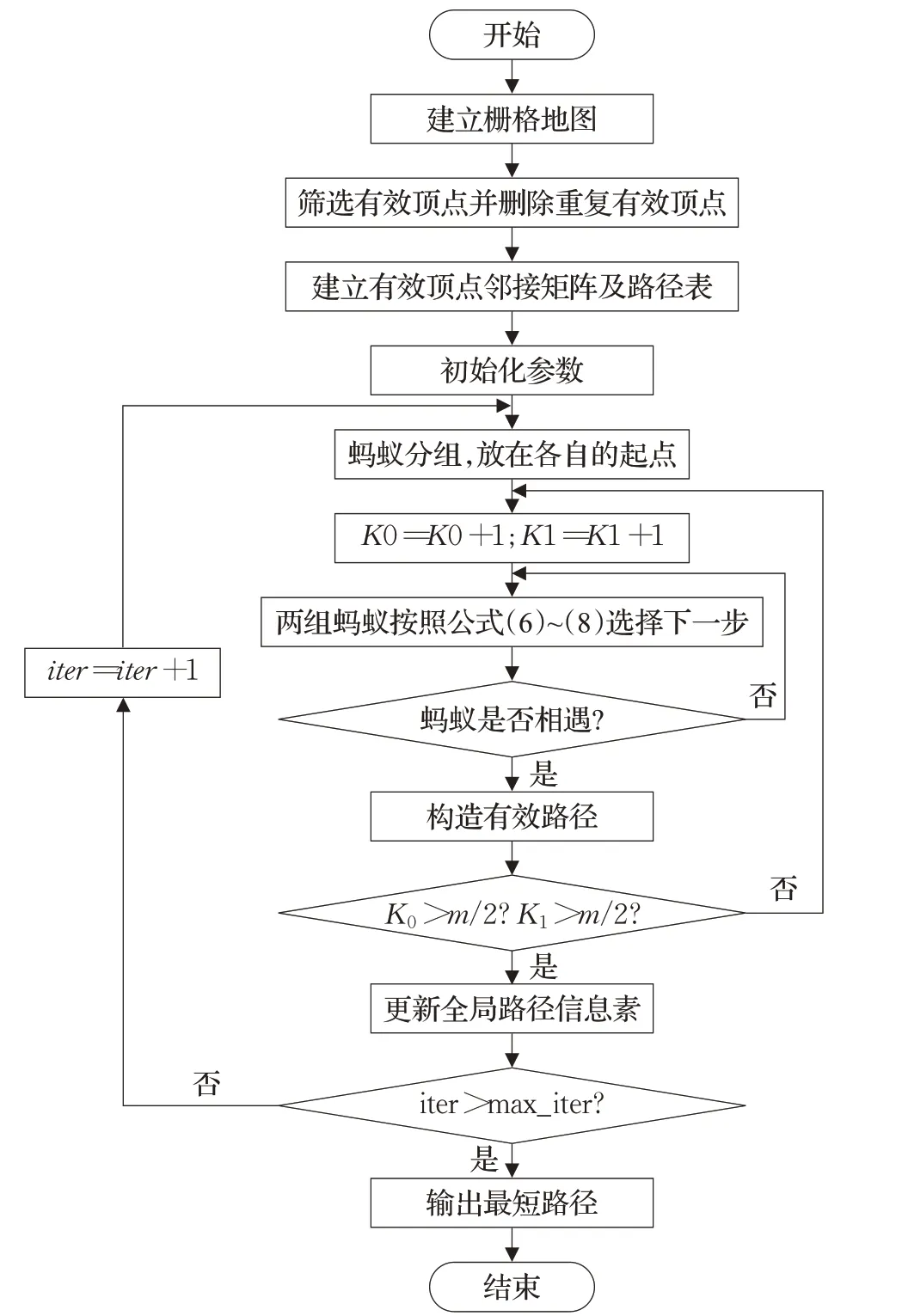
圖5 改進蟻群算法流程圖Fig.5 Flow chart of improved ant colony algorithm

5 實驗仿真與分析

為驗證改進算法的可行性、有效性和優越性，在MATLAB 2016a上進行仿真實驗。從以下幾個方面進行實驗驗證：在稍微復雜的柵格地圖環境中，在相同的參數條件下，將單獨改進的單向有效頂點（方案1）、雙向有效頂點（方案2）、雙向有效頂點+改進啟發函數（方案3）、雙向有效頂點+改進狀態轉移規則（方案4）和雙向有效頂點+改進揮發系數（包括限制信息素范圍）（方案5）依次和傳統算法進行仿真對比，然后將整體改進方法分別與傳統算法和文獻[16]進行仿真對比分析，驗證改進方法的可行性以及改進算法的優越性。在大型復雜柵格地圖環境下，將改進算法與傳統算法和文獻[16]算法（使用文獻參數）進行對比分析，驗證改進算法的優點。

仿真參數設置分別為：

螞蟻數目為80，最大迭代次數為100，α=1,β=2,Q=50,q0=0.4,a=1.5,b=2。以下結果都是算法運行50次的平均值。

5.1 20×20復雜環境

方案1~5、傳統算法、文獻[16]算法和本文算法最優路徑圖分別如圖6~13所示，以及仿真結果數據如表1所示。

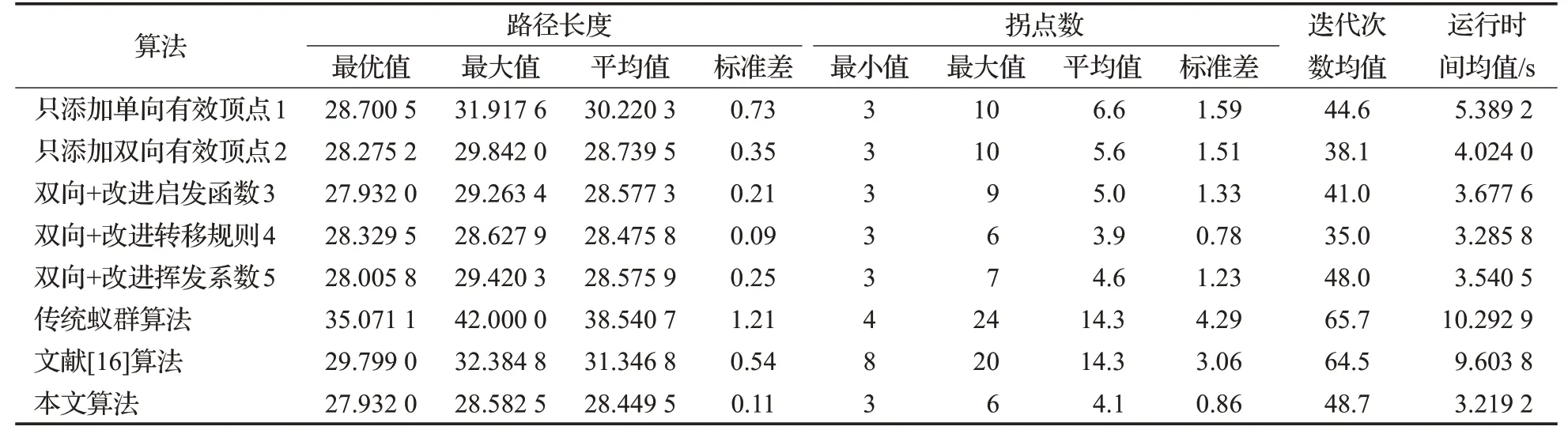
表1 20×20復雜環境下的仿真結果Table 1 Simulation results under 20×20 complex environment

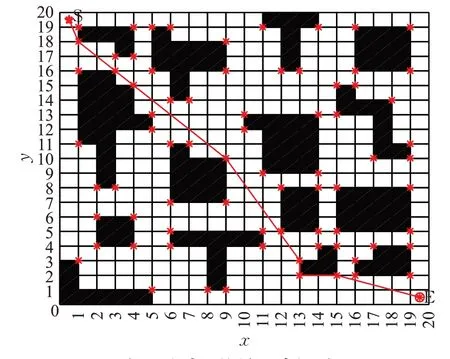
圖6 方案1的最優路徑圖Fig.6 Optimal path diagram of scheme 1

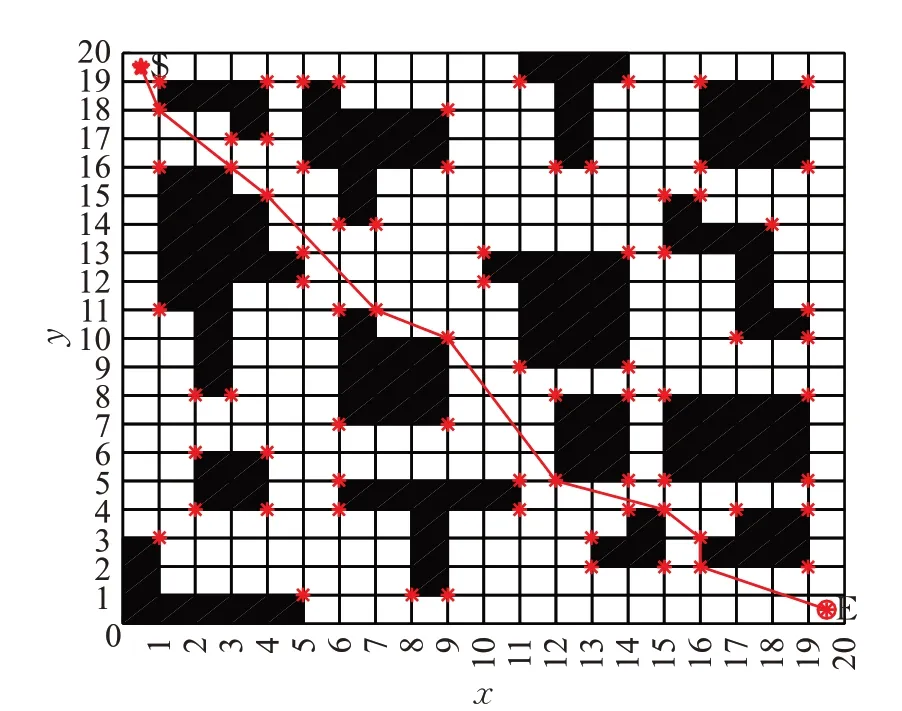
圖7 方案2的最優路徑圖Fig.7 Optimal path diagram of scheme 2

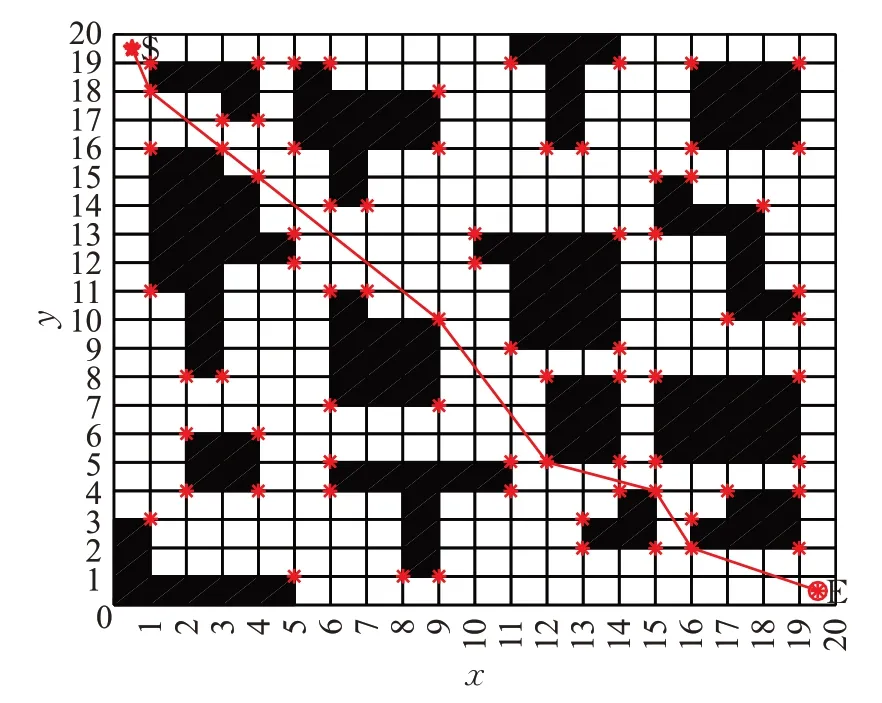
圖8 方案3的最優路徑圖Fig.8 Optimal path diagram of scheme 3

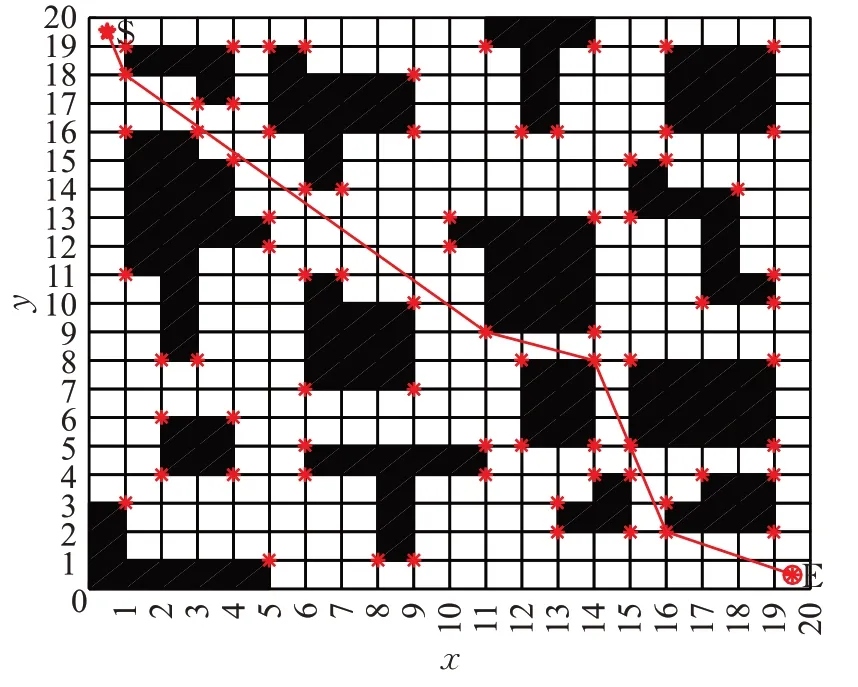
圖9 方案4的最優路徑圖Fig.9 Optimal path diagram of scheme 4

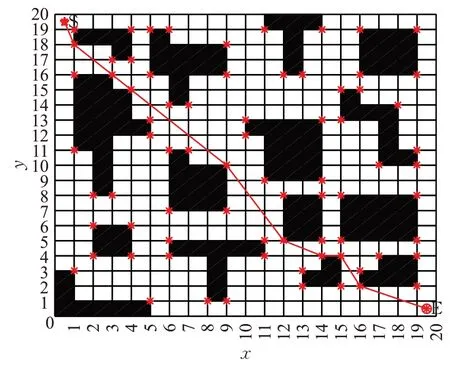
圖10 方案5的最優路徑圖Fig.10 Optimal path diagram of scheme 5

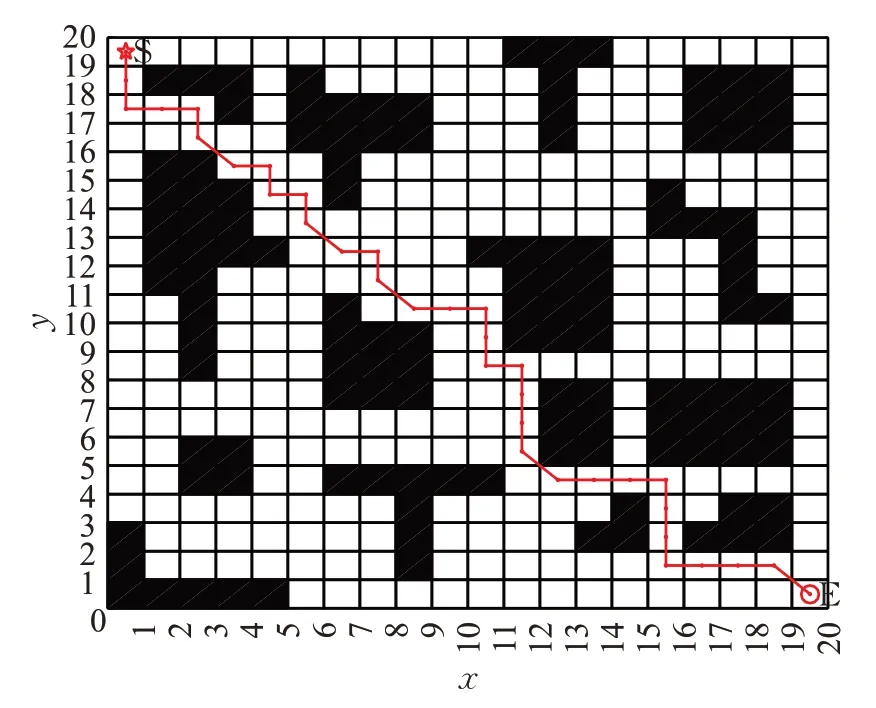
圖11 傳統算法的最優路徑圖Fig.11 Optimal path graph of traditional algorithm

在驗證改進算法整體改進的優越性前，設置梯度方案，即由于改進算法的特殊性，不能直接將某一個改進的點加入傳統算法進行比較，而是在單向有效頂點路徑搜索基礎上設置梯度方案，驗證改進點的可行性。梯度方案為方案1~5，分別對應單獨添加有效頂點，單獨使用有效頂點，雙向有效頂點+改進啟發函數，雙向有效頂點+改進轉移規則和雙向有效頂點+改進揮發系數。

經仿真數據可知，在最優路徑、拐點數和收斂速度方面，單向有效頂點都優于傳統算法，驗證有效頂點的可行性和優越性，在單向基礎上添加反向，即雙向有效頂點，在最優路徑、拐點數和收斂速度方面進一步改善，說明雙向搜索的優越性，然后在雙向的基礎上分別加入改進啟發函數、改進轉移規則和改進揮發系數，在拐點數和算法運行時間上，再一次改善，在最短路徑或者最短路徑的穩定性上也得到相應的改善，驗證改進點可行性和有效性。

最后將整體改進算法與傳統算法和文獻[16]算法進行比較，三種算法都能找到各自的最短路徑，分別為27.932 0、35.071 1和29.799 0，由此可知，改進算法找到的路徑最短，在拐點數和收斂速度方面占有較大優勢，總之，改進算法得到的最短路徑、拐點數和收斂速度都優于傳統算法和文獻[16]算法。

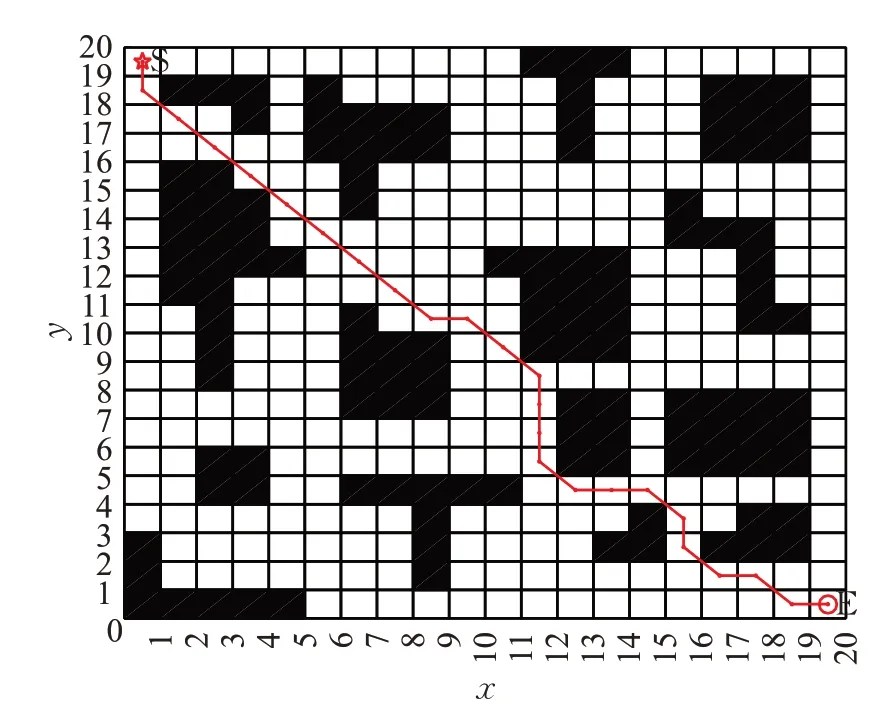
圖12 文獻[16]的最優路徑圖Fig.12 Optimal path graph of reference[16]

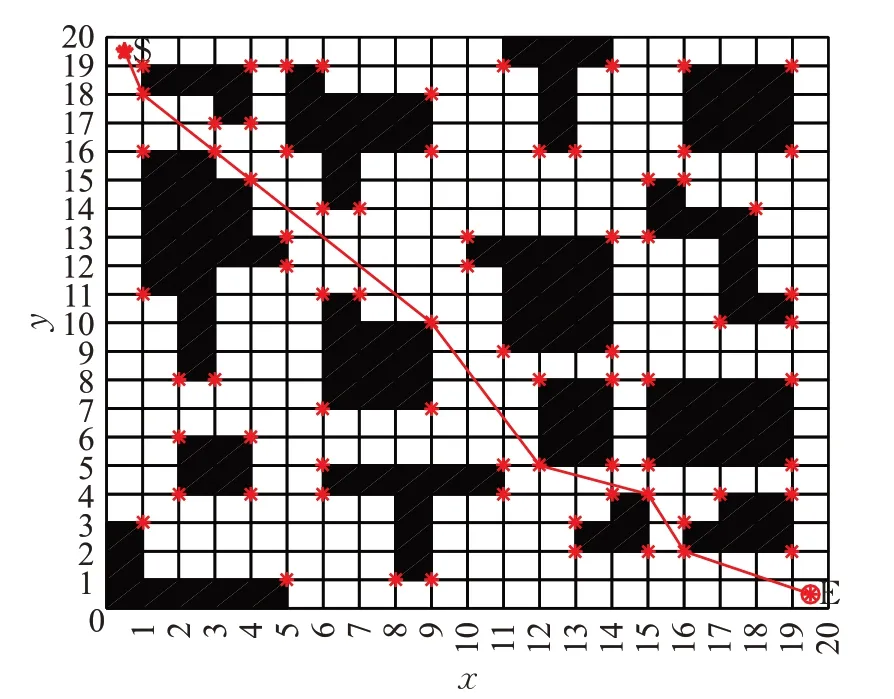
圖13 本文算法的最優路徑圖Fig.13 Optimal path graph of proposed algorithm

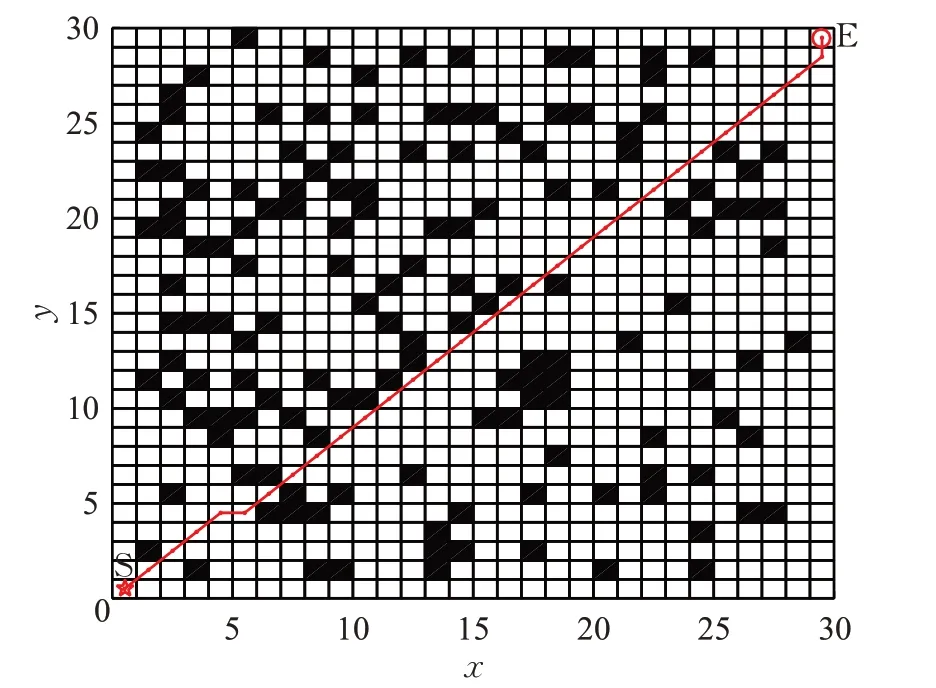
圖15 文獻[16]算法最優路徑圖Fig.15 Optimal path of algorithm in reference[16]

5.2 30×30復雜的環境

為進一步驗證改進算法也能適用于更加復雜環境，因此在復雜環境下進行仿真。傳統算法、文獻[16]算法和本文算法的最優路徑圖分別如圖14~16所示，以及三種算法仿真結果數據如表2所示。

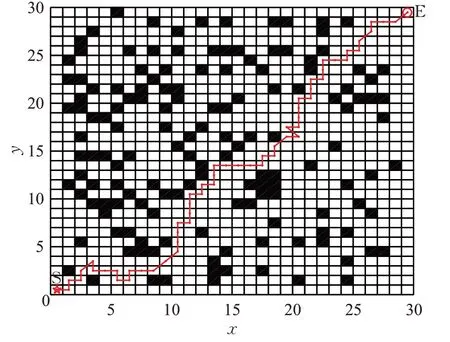
圖14 傳統算法的最優路徑圖Fig.14 Optimal path graph of traditional algorithm

表2 30×30復雜的環境下三種算法的仿真結果Table 2 Simulation results of three algorithms in 30×30 complex environment

通過比較仿真數據，改進算法得到的路徑最短為41.061 1，拐點數最少為2，路徑幾乎接近起點和終點的連線，且它們的平均值和標準差最小，文獻[16]次之，傳統算法最大，平均值和標準差的大小能夠反映在最小值附近的波動大小以及穩定性，也可以反映該最小值出現機會的大小，如在50次的運行結果中，傳統算法找到的最短路徑59.899 5出現1次，相應的平均值和標準差較大，改進算法找到的最短路徑41.061 1出現32次，相應的平均值和標準差較小。由于傳統算法盲目性大，啟發信息較弱，在路徑搜索時，拐點較多，有時出現回環交叉，遠離目標行走，導致路徑長度增加。在收斂速度和算法運行時間方面，改進算法和文獻[16]算法都優于傳統算法，其中改進算法稍遜于文獻[16]算法。

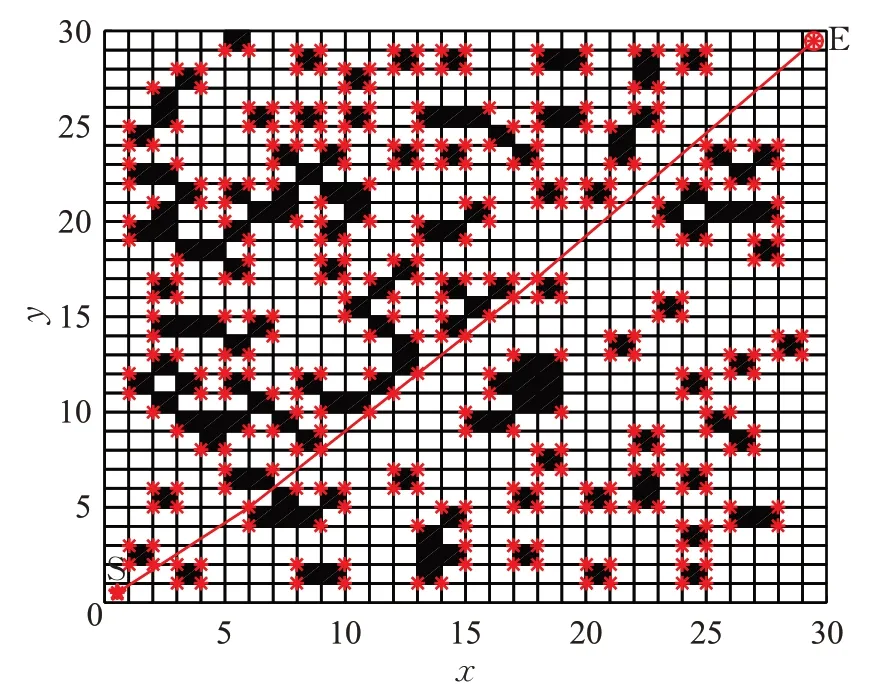
圖16 本文算法最優路徑圖Fig.16 Optimal path graph of proposed algorithm

6 結束語

在靜態的全局路徑規劃中，本文對傳統蟻群算法的不足，提出了一種改進雙向蟻群算法。雙向蟻群算法結合障礙物有效頂點進行路徑搜索，能夠快速找到最優解且得到的路徑拐點相對較少；改進的啟發函數與當前有效頂點和下一可選有效頂點有關，能夠實現一步或多步行走（相對于傳統算法）；改進的狀態轉移規則能夠加快收斂速度；改進的揮發系數能夠避免陷入早熟。基于以上的改進，本文算法能夠很好地適用于不同尺度和不同復雜程度的柵格地圖。總之，從小型簡單的柵格地圖中，已經證明了改進算法的優越性，在大型復雜柵格地圖中能夠明顯地驗證改進算法可行性、有效性和優越性。