青島地區大氣加權平均溫度模型優化

范士杰，劉兆健*，陳 巖，顧宇翔，劉焱雄

（1.中國石油大學（華東） 海洋與空間信息學院，山東 青島 266580；2.自然資源部第一海洋研究所，山東 青島 266061）

大氣加權平均溫度（Tm）是對流層濕延遲轉化為大氣可降水量的重要參數[1]。精確獲取Tm需對氣象資料進行復雜的積分運算，但大部分地區不具備測定相關氣象數據的條件，因此一般采用經驗模型對其進行估計。現有的Tm經驗模型主要是根據Tm與氣象參數（地表溫度Ts、水氣壓es）的相關性而構建的，且多為考慮Ts的Tm-Ts線性模型，如Bevis M[2]等利用北美13個探空站資料建立了最早的Tm模型。由于建模資料的時空差異，導致Tm模型應用于部分區域時的精度有所下降，LAN Z Y[3]等發現Bevis模型應用于全球部分地區時會有較大的系統性誤差；黃良珂[4]等發現GPT2w模型計算的Tm在中國東北和西部地區的誤差較大，而在低海拔地區尚可保持較高精度；胡應劍[5]等發現GPT2w模型在新疆地區有-3～-4 K的系統性偏差，且1 格網分辨率的GPT2w模型計算結果優于5 分辨率的結果。因此，眾多學者對精度更高的本地化Tm模型開展了研究[6-10]，李黎[11]等基于探空資料建立了湖南地區本地化Tm模型；張化疑[12]等利用MM4中尺度氣象模式的溫度、水汽等資料構建了渤海地區的Tm-Ts線性模型；李斐[13]等基于青島探空站2009－2011年的探空資料建立了青島地區Tm線性模型，上述模型均取得了一定的效果。

研究發現，Tm除了與Ts有強線性相關性外，還與es具有指數關系，且線性Tm模型可能存在周期性殘差[14-15]。鑒于青島地區目前還沒有考慮單、雙因子以及周期性誤差改正的Tm模型的相關研究，本文基于IGRA提供的青島探空站2013－2019年的探空資料，采用單站建模方法構建和優化了青島地區本地化Tm模型，并結合現有Tm模型對本地化優化模型進行了精度對比和分析。

1 Tm模型

利用數值積分法求解Tm是目前公認的最優方法[16]， 精度較高且容易實現。對測站上空氣象資料進行垂向積分，即

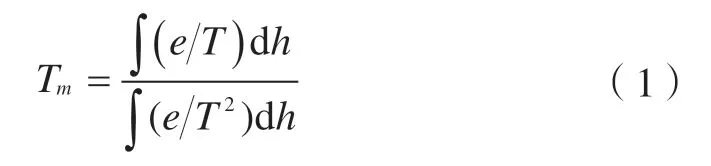
式中，e為站點水汽壓，單位為hPa；T為絕對氣溫，單位為K；h為站點上空大氣分層高度，單位為km。

由于探空資料等數據源多為分層記錄，因此一般采用式（1）的離散化形式，則有：

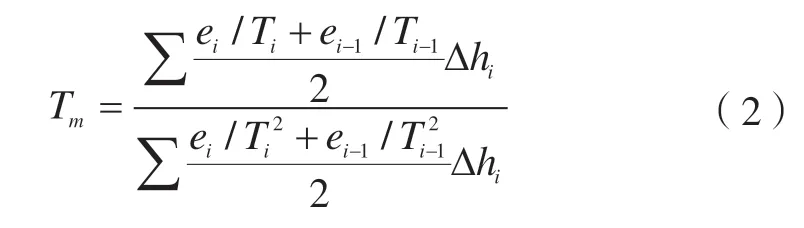
式中，ei、ei-1、Ti、Ti-1分別為第i層大氣上界和下界的水汽壓和氣溫；Δhi為第i層大氣層的高度。ei并不是直接記錄的觀測值，可利用飽和水汽壓和露點溫度計算得到。

絕大部分地區不易測得分層記錄的氣象資料，因此無法通過式（2）精確計算Tm值；但可利用容易獲取的Ts和es建立與Tm的聯系，從而求解本地區的Tm值。根據Tm與Ts的線性關系以及Tm與es的指數關系，可建立3種本地化單因子、雙因子模型，即

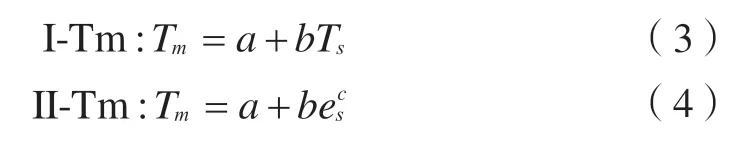
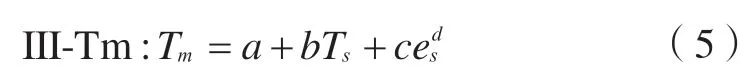
式中，a、b、c、d為擬合系數，可基于原始建模數據采用最小二乘法擬合得到。式（3）、式（4）為單因子模型，式（5）為雙因子模型，

2 青島本地化Tm模型的構建和優化

2.1 單因子和雙因子Tm模型構建

本文采用IGRA提供的青島探空站（36.066 7 N、120.333 3 E，77.0 m）2013－2019年每天0時和12時 的探空數據進行青島本地化Tm模型的構建和誤差分析。首先利用該站點2013－2017年的探空數據和積分Tm值分別擬合得到上述3種單因子和雙因子模型的系數，如表1所示，進而建立本地化Tm模型；然后利用該站點2018－2019年的探空數據，以積分Tm結果為參考值，對上述3種本地化Tm模型進行誤差分析，殘差序列如圖1所示，其中灰色部分為殘差值，黑色部分為三角函數對Tm殘差的擬合結果。

表1 3種本地化Tm模型的擬合系數

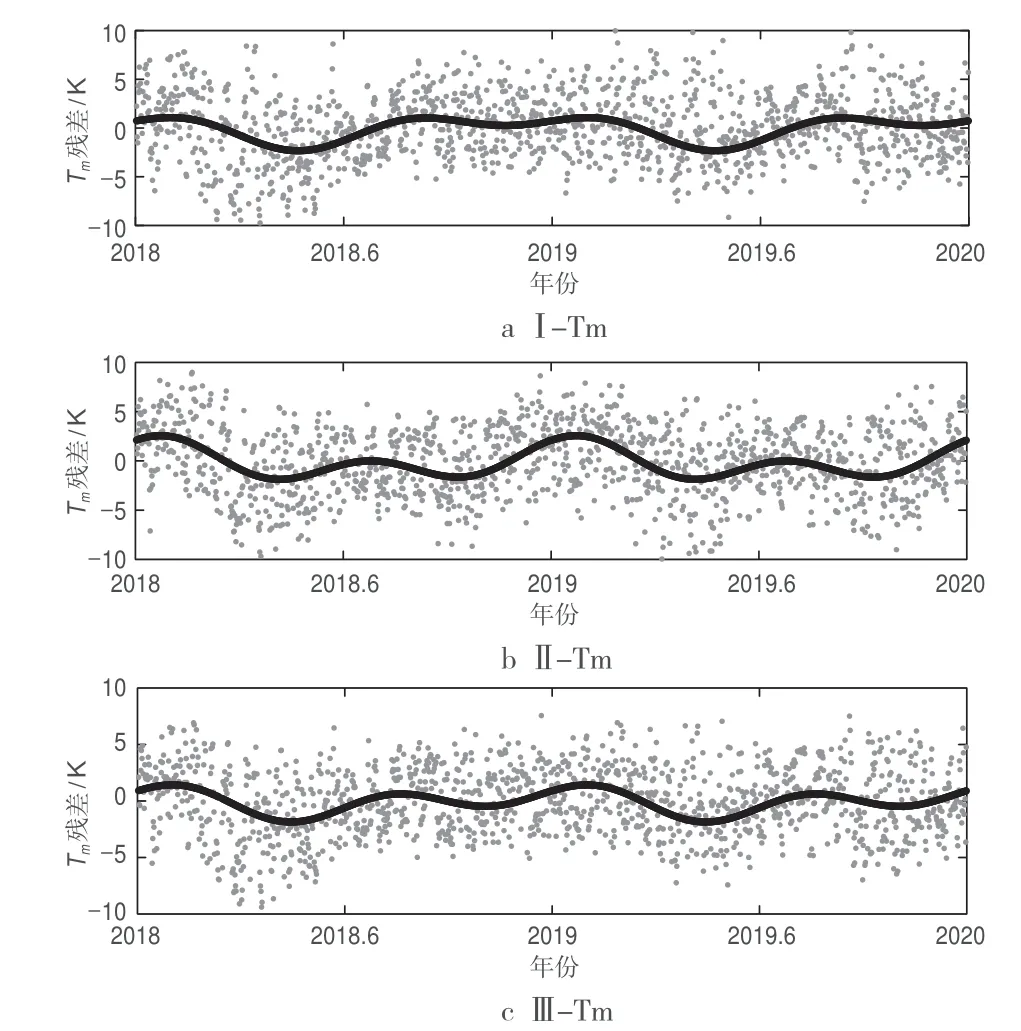
圖1 單因子和雙因子Tm模型的殘差序列

由圖1可知，3種Tm模型的殘差均包含明顯的年、半年和季節性周期誤差影響，且各模型的周期基本一致。3種Tm模型的平均偏差和均方根誤差如表2所示，可以看出，平均偏差均在 0.2 K以內，說明3種模型均無明顯的系統性偏差；相較于單因子模型，雙因子模型的精度略優。

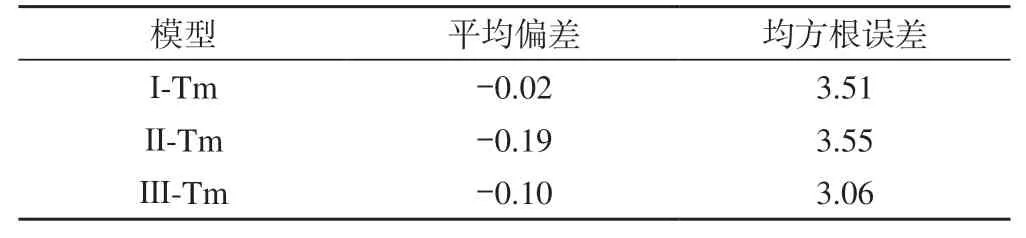
表2 3種本地化Tm模型的平均偏差和均方根誤差/K

2.2 顧及周期性誤差改正的Tm模型優化

由于上述3種Tm模型的誤差均存在明顯的周期性變化，為減弱這種誤差影響，本文考慮在模型中加入周期性改正項。對兩種單因子Tm模型（I-Tm、Ⅱ-Tm）和雙因子Tm模型（Ⅲ-Tm）進行優化，在原模型的基礎上加入年周期、半年周期以及季節性周期改正，得到3種優化模型IB-Tm、IIB-Tm和IIIB-Tm。具體表達式為：

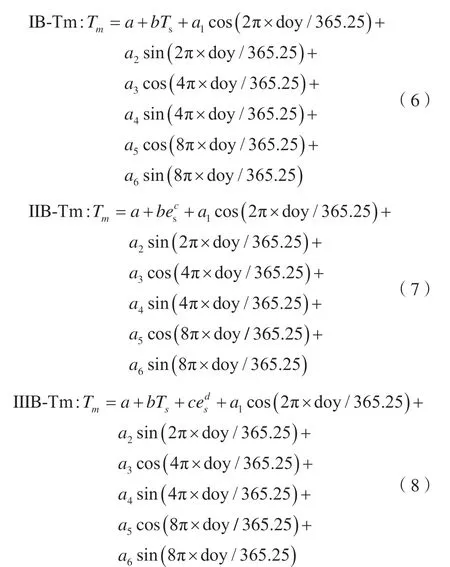
式中，doy為年積日；a1、a2、a3、a4、a5、a6為周期誤差改正項擬合系數。

本文首先利用青島探空站2013－2017年的探空數據求取上述3種優化模型的擬合系數，結果如表3所示；然后利用青島探空站2018－2019年的探空數據，以積分Tm結果為參考值，對優化模型進行精度驗證和誤差分析。3種優化模型IB-Tm、ⅡB-Tm和ⅢB-Tm的殘差時間序列如圖2所示，其中灰色部分和黑色部分仍分別為Tm殘差值和三角函數擬合結果。對比圖1與圖2中各模型的殘差分布發現，3種優化模型IB-Tm、ⅡB-Tm和ⅢB-Tm均很好地消除了3種原模型的周期性誤差，使得Tm殘差擬合結果更趨向于直線，分布更合理。

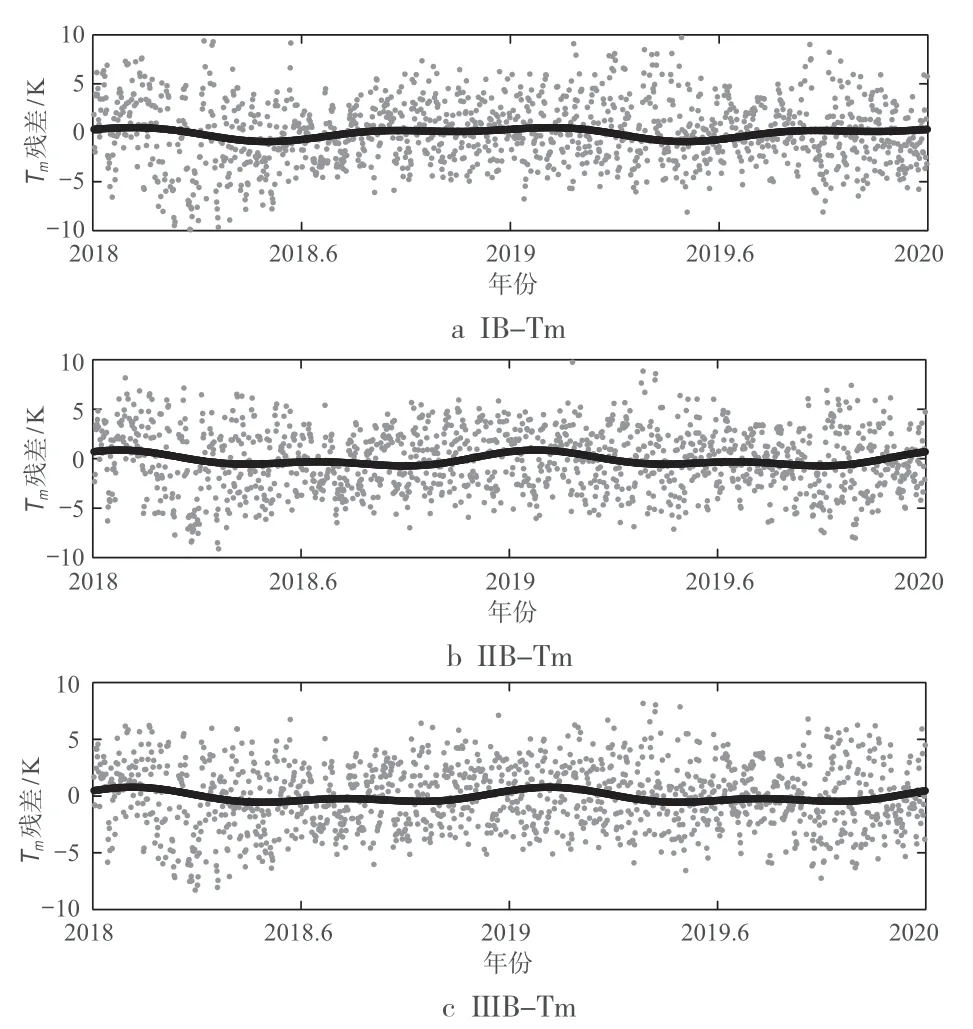
圖2 考慮周期性誤差改正的優化Tm模型的殘差序列

表3 3種優化Tm模型的擬合系數

3種優化Tm模型的平均偏差和均方根誤差如表4所示，可以看出，3種優化模型無明顯系統性偏差，且均方根誤差均比原模型有所減小。考慮到3種優化Tm模型能明顯削弱原模型的周期性誤差，且單因子和雙因子模型間的精度差異較小，以及氣象資料中Ts比es更方便獲取等因素，本文最終采用基于單因子Ts的優化模型IB-Tm作為青島地區新的Tm模型，并記為Tm_QD。

表4 3種優化Tm模型的平均偏差和均方根誤差/K

3 青島地區本地化Tm模型的對比分析

為進一步驗證青島本地化模型Tm_QD的精度，本文選取3種常用的現有的Tm模型與之進行對比，分別為Bevis模型（Tm=70.2+0.72Ts）、張化疑[12]等建立的 渤海地區Tm模型（Tm=-25.022+1.044Ts）和李斐[13]等建立的青島地區Tm-Ts模型（Tm=-0.557 5+0.97Ts），簡記為Bevis（1994）、Zhang（2010）和Li（2018）。以2018－2019年青島探空站每日兩次的探空資料以及歐洲中尺度天氣預報中心（ECMWF）發布的第五代模式數據產品——ERA5氣象再分析數據為參考，上述4種Tm模型的平均偏差和均方根誤差如表5所示。

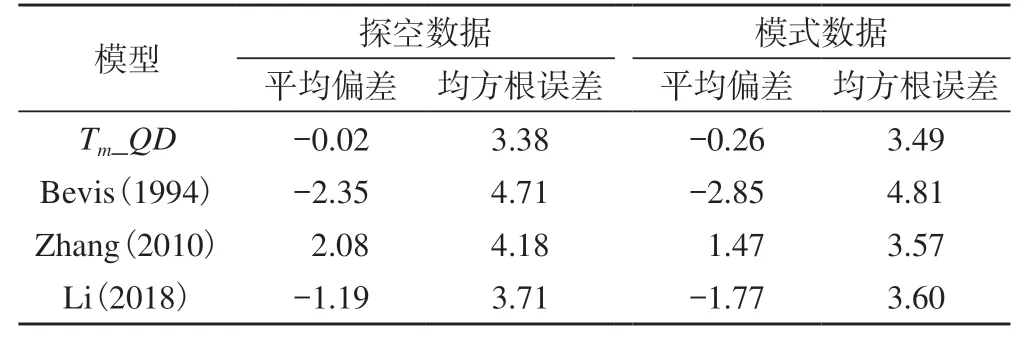
表5 4種Tm模型相對于探空和模式數據的精度對比/K

由表5可知，以探空和模式數據為參考，青島本地化優化模型Tm_QD的平均偏差較小，沒有明顯的系統性偏差，其余3種模型均存在1～3 K的系統性偏差；Tm_QD的均方根誤差最小，Bevis（1994）的系統性偏差和均方根誤差均為最大；相對于探空數據，Tm_QD的精度比Bevis（1994）、Zhang（2010）和 Li（2018）分別提升約28%、19%和9%；相對于模式數據，Tm_QD的精度比Bevis（1994）提升了約27%，比其他兩種模型的精度也略有提升。同為本地化模型，Tm_QD比Li（2018）的系統性偏差更小，精度也更高，其原因主要應與Tm_QD考慮了周期性誤差改正、建模所用探空數據更新以及時間更長等因素有關。

4 結 語

本文基于IGRA提供的青島站探空資料，考慮了單、雙因子以及周期性誤差改正等因素，采用單站建模方法開展了青島地區本地化Tm模型的構建和優化研究；并以探空數據和模式數據為參考，將青島地區本地化優化模型Tm_QD與現有常用模型進行對比和精度分析。結果表明：①Tm_QD模型基本消除了周期性誤差影響，無明顯系統性偏差，且精度比現有常用Tm模型高；②本地化Tm模型的精度優于區域或全球模型，但本地化模型也應進行及時更新，以保證模型的精度。