基于分數階理論的鋰離子電池 高頻等效電路模型

吳 健 尹 澤 李 豪 趙 濱 季 巧 孫丙香

（北京交通大學國家能源主動配電網技術研發中心 北京 100044）

0 引言

鋰離子電池由于在能量密度、耐用性和環境保護方面的優勢而在汽車和軌道交通領域中越來越受歡迎。在實際應用中，鋰離子電池通常與DC-DC變換器連接來控制能量流動，這就會產生高頻噪聲和電流紋波，使電池在工作時受到高頻激勵。因此，需要開發一種新的模型，能夠更好地描述電池的高頻行為，有利于優化電力電子電路的控制策略以及無源元件的設計。

常見的電池模型主要有黑箱模型、電化學模型（Electrochemical Model, EM）和等效電路模型（Equivalent Circuit Model, ECM）。黑箱模型基于機器學習方法，需要大量的實驗數據進行訓練，但沒有設計明確的模型結構來模擬電池內部的反應[1]。電化學模型是基于電化學原理建立的，可以從本質上反映電池外部特性與內部參數之間的關系。盡管電化學模型具有較高的精度，但這些模型存在明顯的缺點：模型結構復雜、參數識別困難以及運算速度低。因此，電化學模型應用于實際車輛的電池管理系統（Battery Management System, BMS）中，使用效果并不理想[2-3]。而由理想電氣元件組成的等效電路模型已成功地應用于荷電狀態（State of Charge, SOC）、健康狀態（State of Health, SOH）和能量狀態（State of Energy, SOE）的估計[4-6]。

但是，整數階等效電路模型不能準確地描述電池的動態過程，階數會影響其準確性。具體來說，低階模型精度較低但是計算量小，高階模型精度較高但是計算量大，在實際使用中通常根據應用領域和需求的不同來選擇使用低階模型還是高階模型。文獻[7]對常用的整數階模型進行了深入的比較和討論。近年來，隨著分數階微積分應用的推廣，越來越多的學者將分數階等效模型用于電池的研究。使用分數階阻抗元件，如恒相位元件（Constant Phase Element, CPE）（通常記為Q）和Walberg阻抗可以更準確地描述鋰離子電池的電化學過程，如電荷轉移、雙電層效應、物質轉移和擴散等，既提高了精度，又有效地解決了模塊過多引起的計算復雜問題。文獻[8]使用包含一個CPE的分數階模型模擬不同條件下的電壓曲線，結果表明，它的精度要高于不同階次的整數階模型。文獻[9]對幾種不同結構的分數階模型進行比較研究，分析了計算準確性和計算負擔與模型結構之間的關系。

然而，很少有研究者去專門關注鋰離子電池的高頻響應，等效電路中的高頻部分通常由電感L代替[10]，甚至被忽略[11]。也有研究者進行了高頻激勵的阻抗分析，并提出了與歐姆電阻并聯的電感作為等效電路模型中的高頻部分[12-13]，在這些文獻中為了便于進行基于等效電路的仿真使用了整數階模型，更加關注鋰離子電池在高頻范圍內不同條件下的行為或電流在模型內不同支路中的分布，對于模型的精度沒有較高的要求。同樣，文獻[14]使用多個RL和RC串聯來建立高頻模型，在時域和頻域的響應上都有著較高的精度，但是模型較為復雜、計算量大。也有相關研究者將典型分數階模型中的整數階電感L替換為分數階元件，在更高頻率的阻抗響應上有著較高的精度[15]，但是沒有在時域響應上進行驗證，無法在實際中使用。此外，文獻[16-17]通過建立復雜傳輸線模型或包含趨膚效應的模型來研究電磁干擾對電池的影響，其頻率遠高于電力電子設備的典型開關頻率，本文不再贅述。

本文基于電化學阻抗譜（Electrochemical Impe- dance Spectroscopy, EIS）建立了幾種高頻模型，通過使用分數階模型，在保證模型精度的同時降低了模型的復雜度。然后對幾種模型在時域上進行參數辨識，通過比較其響應精度和計算量，給研究人員提供參考，為鋰離子電池選擇合適的高頻模型。同時研究發現，根據EIS擬合得到的最優模型并不一定在時域擬合中也是最優。

1 分數階模型

1.1 電化學阻抗譜

EIS是研究電池電化學性能的重要手段，通過測量不同頻率響應信號與擾動信號的比值，來獲得相應頻率下的阻抗值。EIS具有以下三個特點：①電化學系統受到小幅值正弦信號的擾動，因此電動勢與電流之間存在線性關系，簡化了測量結果的數學處理；②陽極和陰極的反應過程在電極上交替發生，即使測量時間較長，也不會積累極化，是一種“準穩態方法”；③EIS是一種頻域測試方法，可以測量較寬的頻率范圍，從而可以獲得比傳統電化學方法更多的動力學信息和電極界面信息[18]。

一種典型鋰離子電池EIS及其等效電路模型如圖1所示，該圖可分為低頻直線、中頻半橢圓和高頻感性部分三段。一般認為，低頻直線與正負極鋰離子擴散動力學有關，通常用Walberg阻抗（見圖1中ZW）表示；中頻半橢圓與電荷轉移反應和雙電層電容有關，通常用電阻與CPE（見圖1中CQ）并聯表示；高頻感性部分代表電池的電感特性以及測試電纜和連接裝置帶來的感性構成，通常用電感元件表示[19]。此外，圖中與實軸相交的部分代表鋰離子電池的歐姆內阻。

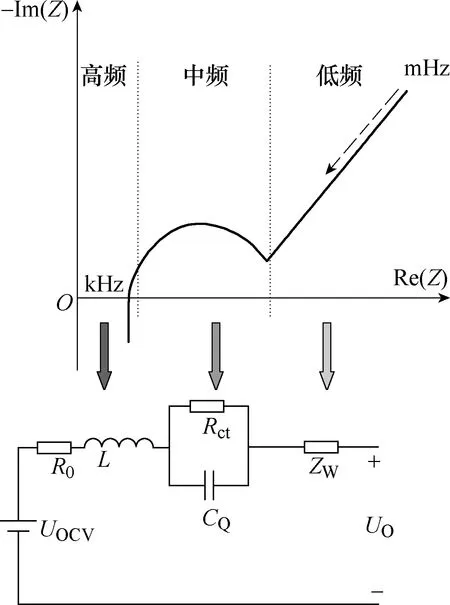
圖1 一種典型鋰離子電池EIS及其等效電路模型 Fig.1 A typical EIS of lithium-ion battery and its equivalent circuit model

通常根據EIS建立的模型是不唯一的，通過對EIS進行擬合來獲得模型中每個參數，并驗證模型的準確性。本文采用自適應差分進化算法進行擬合，具有較好的全局收斂性，具體的算法過程如下[20]：

（1）初始化個體數目NP、變量維數D、最大進化代數G、初始變異算子0F、交叉算子CR和閾值T。

（3）根據式（1）生成變異種群iv，即

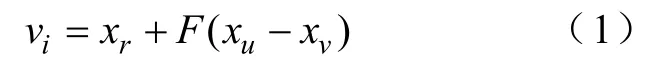
其中

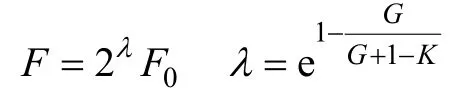
式中，r、u、v為1～NP中隨機選取的相異整數；F為自適應變異算子。

（4）將在步驟（3）中生成的iv和當前的種群K ix進行交叉生成交叉種群iu，即

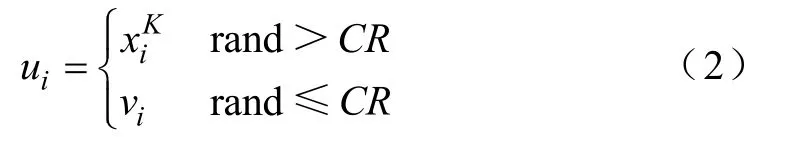
式中，rand為[0, 1]之間的隨機數。

（5）對邊界條件采用在可行域中隨機產生參數向量的方式進行處理。

（6）計算步驟（4）中生成的ui的目標函數f(ui)，與原種群的目標函數進行“一對一”選擇操作，若，則ui將代替；否則，將保留到下一代，即

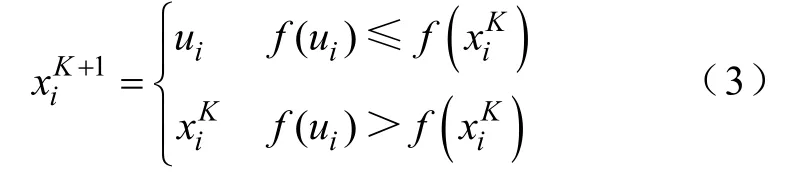
（7）判斷是否滿足終止條件：若滿足，則結束搜索過程，輸出優化值；若不滿足，則繼續進行迭代優化。

用于EIS擬合的目標函數[11]為

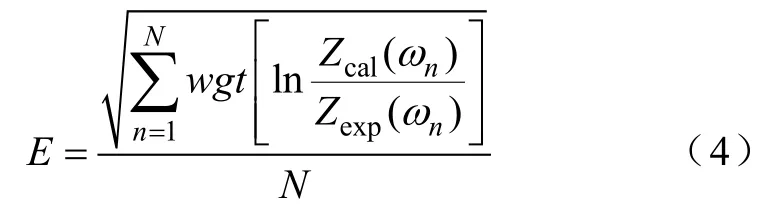
其中

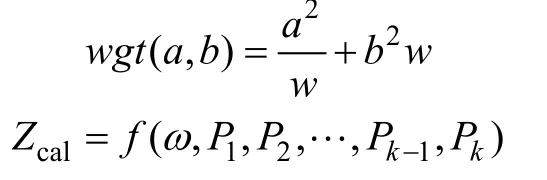
式中，wgt為對數距離函數，表示某一頻率下計算數據與實驗數據的復合偏差；Zcal和Zexp分別為計算阻抗和測量阻抗；a和b分別為對數運算后結果的實部和虛部；w為擬合過程中相位的權重大小，默認值為2.2；N為實驗數據的長度；Pk為模型中的第k個參數。在擬合過程中的目標是使總誤差E最小。與線性加權相比，運用對數距離函數可以更好地適應參數未知的大范圍變化，對數的縮放操作也保證了不同量級參數的權重相差不大。

本文研究內容為鋰離子電池高頻模型，因此忽略低頻部分，測量了1Hz～20kHz的中高頻EIS，EIS實測值和擬合結果如圖2所示。針對高頻部分實部增加的現象選擇了三種擬合結果較好的高頻模型，如圖3所示。模型a～模型c簡稱FOM1～FOM3。圖3中，UOCV為開路電壓，LQ為分數階電感，L1、L2為整數階電感，RL為電感支路并聯阻抗，R0為歐姆內阻，Rct為電荷轉移阻抗，CQ為雙電層電容。對三種模型采用上述方法進行擬合后，結果顯示在圖2內，目標函數值分別為EFOM1=0.002 2，EFOM2=0.002 2，EFOM3=0.002。可以看出，三種模型擬合誤差都很小，其中FOM3擬合結果最好，FOM1和FOM2擬合結果幾乎沒有區別。

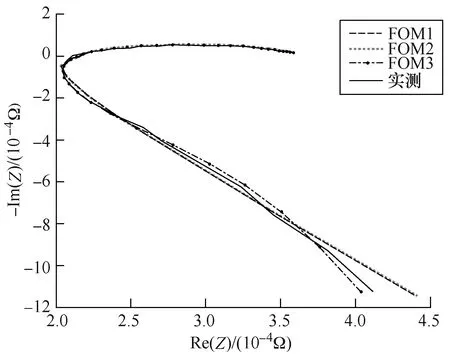
圖2 EIS實測值和擬合結果 Fig.2 EIS measured value and fitting results

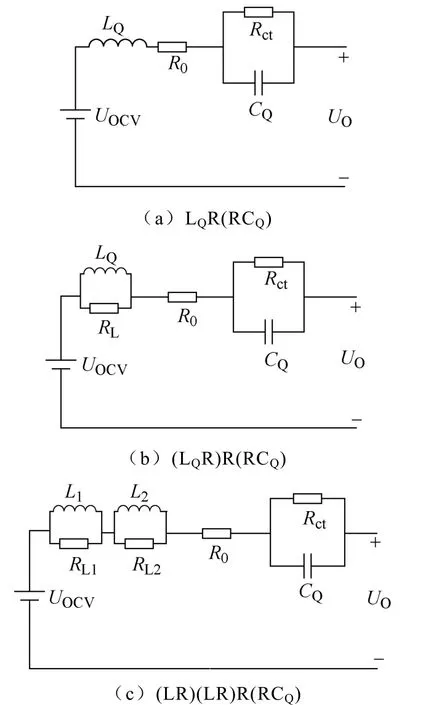
圖3 高頻等效模型 Fig.3 High frequency equivalent model

1.2 分數階模型的數值計算方法

萊布尼茲在1695年就提出了分數微積分算法，然而直到最近才被研究人員應用于工程控制系統、建模和狀態估計中。由于分數階算法更適用于模擬包括傳質、擴散動力學和記憶滯后在內的物理化學系統，因此被用在了鋰離子電池系統的建模中[21]。分數階微積分的連續微分積分算子定義為

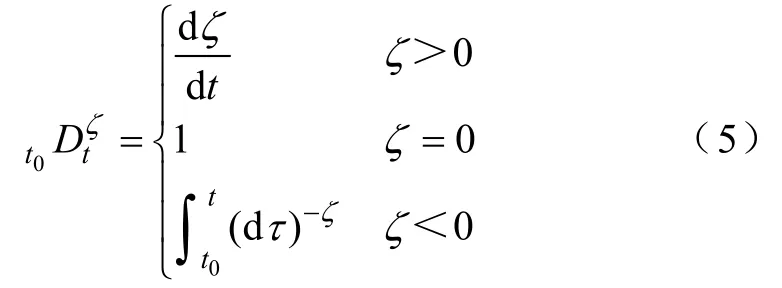
式中，ζ為分數階微積分的階數；0t和t為積分的下限和上限；τ為積分變量。在分數階算法的眾多定義中，有三種是最常用的，分別為Caputo定義、Riemann-Liouville定義和G-L（Grunwald-Letnikov）定義。G-L定義描述了如何直接離散化連續分數階方程，更適合于數值計算，給定函數()f t的ζ階導數的G-L定義為

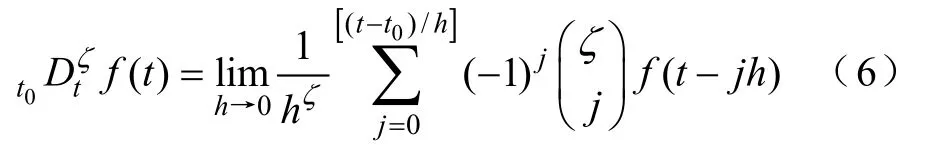
式中，h為采樣周期；的整數部分；為牛頓二項式系數。

以圖3a為例，介紹分數階模型的數值計算，電路中分數階元件LQ、CQ的阻抗表達式分別為

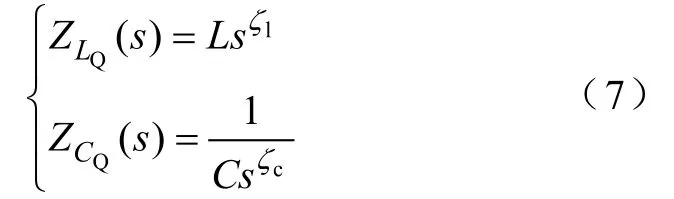
如果電池阻抗可以類似地作為系統傳遞函數處理，輸入為電流、輸出為開路電壓和端電壓之差，則在拉普拉斯域的表達式為

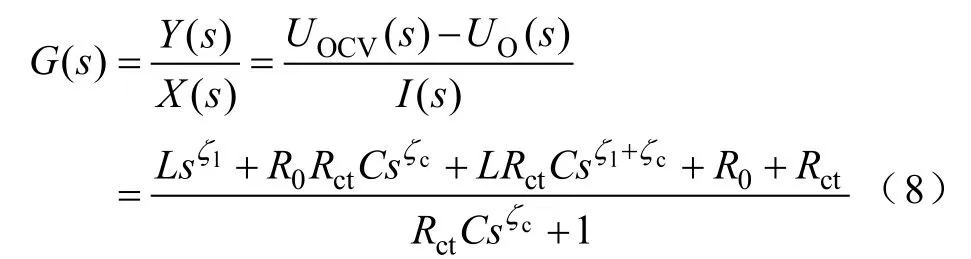
式中，UO為端電壓。

將式（8）轉換到時域中可以得到，系統的分數階微分方程為

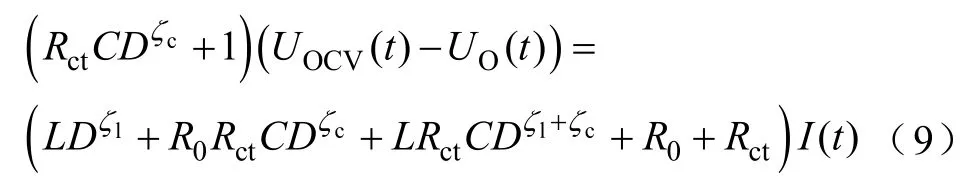
首先定義四個多維變量α、p、β、q分別為

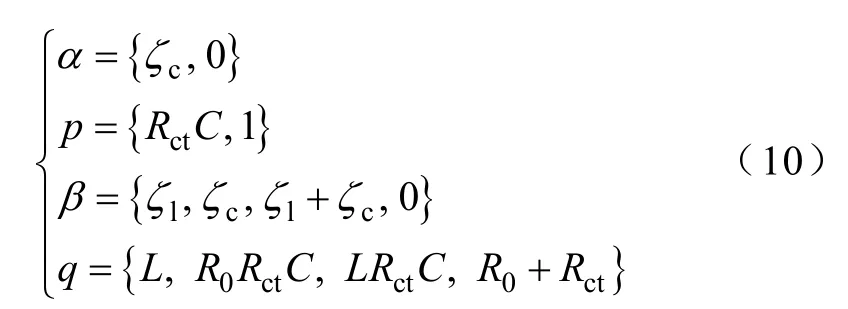
則式（9）可寫成

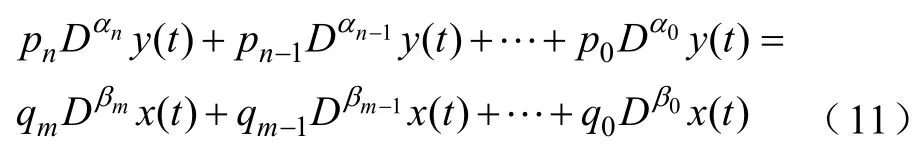
在本例中，n=1，m=3。計算順序如圖4所示，為了計算方便引入了中間變量()u t，然后，根據式（6）可以得到離散化后模型輸出()y t的數值解的一般表達式[22]，即

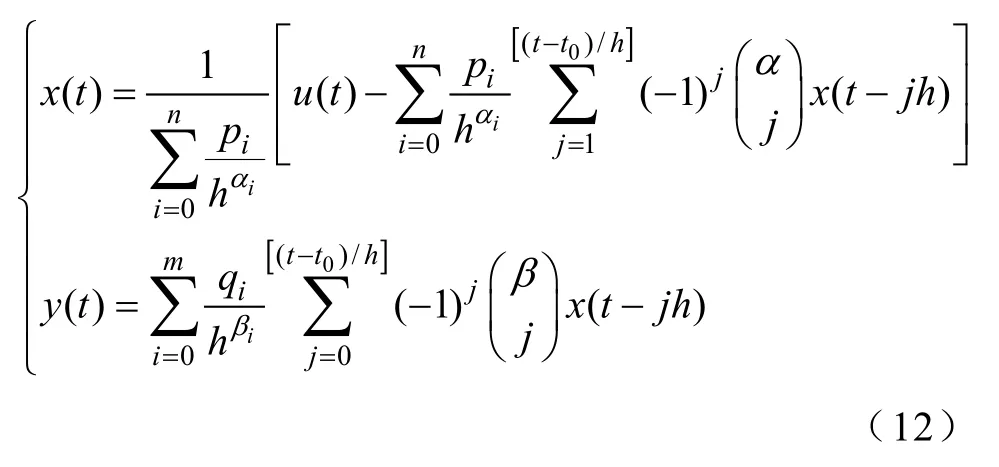
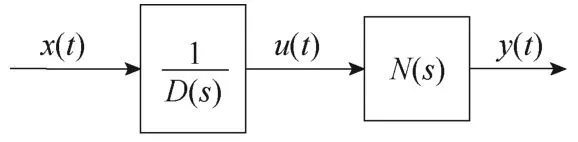
圖4 計算順序 Fig.4 Calculation order

2 實驗驗證

2.1 實驗方案

在本文中，選擇了標稱容量為25A·h的鈦酸鋰離子電池作為實驗對象，鋰離子電池規格見表1。搭建電池測試平臺如圖5所示，實驗設備包括充電機（DC-DC）、dSPACE、工控機（包括PC主機）。其中，dSPACE只用作DC-DC的閉環控制，工控機由于其擴展性高，可以插入不同功能的板卡，具有很強的抗干擾能力，所以用作高頻數據采集，同時兼顧主機功能。為了更精確地觀察電池電壓電流變化的細節，工控機的采樣頻率選擇250kHz。

表1 鋰離子電池規格 Tab.1 Lithium-ion battery specifications

為了模型的參數識別，在25℃的環境溫度下測量了不同頻率紋波電流下的電壓響應。電池的初始SOC為80%，充放電平均電流為1C，分別在1kHz（紋波幅值為±1C）、2kHz（紋波幅值為±0.5C）和4kHz（紋波幅值為±0.25C）的頻率下進行一次20%～ 80%SOC的充放電循環，由于要觀察不同頻率、相同幅值下的電壓響應，在更換DC-DC的電感后再進行一次10kHz（紋波幅值為±1C）的充放電循環。

圖5 電池測試平臺 Fig.5 Battery test platform

2.2 參數辨識結果

模型參數辨識方法框圖如圖6所示，根據電池的實驗數據和仿真數據，利用誤差最小原理進行辨 識[23]。實驗數據包括電池在充放電過程中的電流以及所產生的電壓響應，仿真數據為通過輸入電流值得到的模型輸出的電壓，通過自適應差分進化算法得到最優的模型參數。

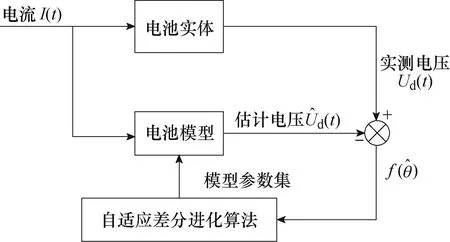
圖6 參數辨識方法框圖 Fig.6 Block diagram of parameter identification method

用于分數階模型參數辨識的目標函數為

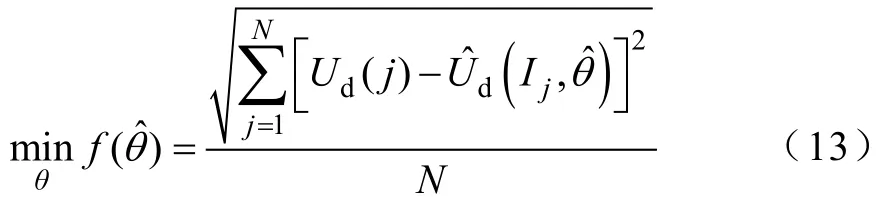
三種模型在不同頻率下進行參數辨識后，不同頻率擬合結果如圖7所示。可以看出，在電流換向時，電池電壓會產生突變，這體現了電池在高頻電流下的電感特性，然后電壓變化變緩則與電池內阻有關。從擬合結果來看，FOM2最接近實測值，FOM1和FOM3在電壓緩慢變化階段不能較好地跟隨。

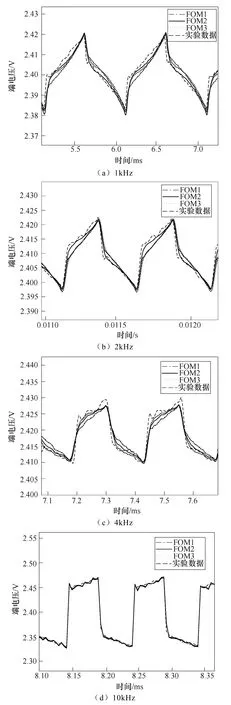
圖7 不同頻率擬合結果 Fig.7 Fitting results of different frequencies

此外，在參數辨識過程中發現FOM2中的分數階元件LQ的階數大于0.95，在部分頻率下甚至大于0.99，非常接近整數階元件。因此，將FOM2中的LQ元件替換為整數階元件L，得到另一種模型(LR)R(RCQ)，簡稱FOM4，如圖8所示。在不同頻率下對FOM4重新進行參數辨識，以1kHz為例，FOM2和FOM4在1kHz下的擬合結果如圖9所示。可以看出，FOM2與FOM4的擬合結果非常接近，同時說明為了準確擬合EIS高頻部分而使用的分數階電感元件并沒有對時域上的擬合精度有較大地提升，這一點在第3節會進一步論述。

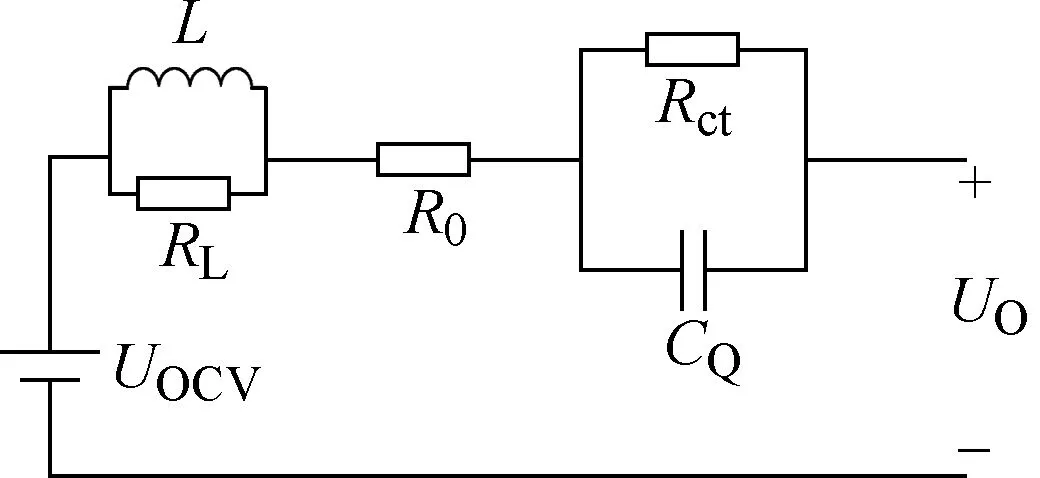
圖8 (LR)R(RCQ)模型 Fig.8 (LR)R(RCQ) model

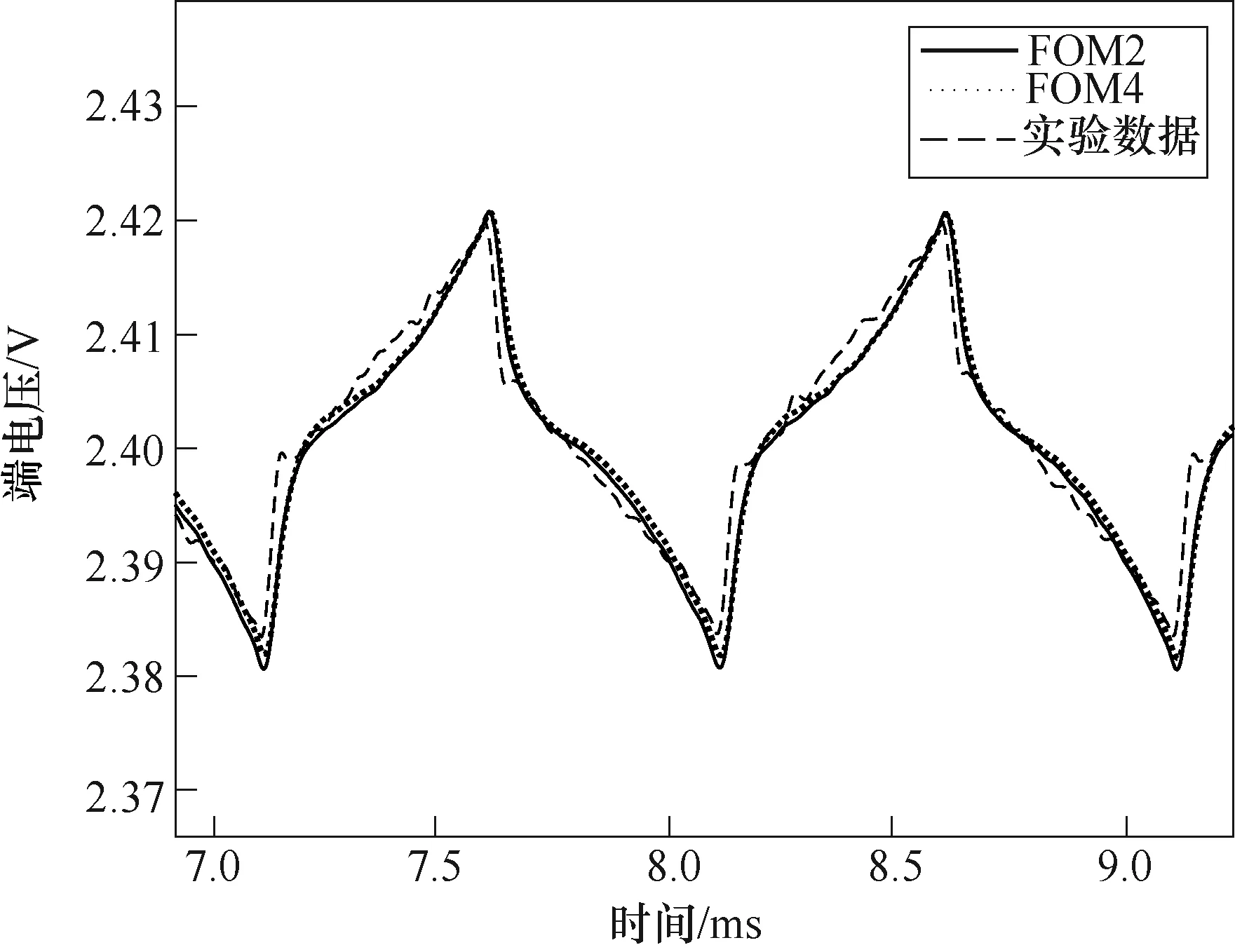
圖9 FOM2和FOM4在1kHz下的擬合結果 Fig.9 Fitting results of FOM2 and FOM4 under 1kHz

3 模型比較

3.1 誤差比較

不同模型的誤差見表2。在表2中比較了這三種模型的方均根誤差（Root Mean Square Error, RMSE）和平均絕對誤差（Mean Absolute Error, MAE）。RMSE是一種常用的度量，用于評估模型預測值與觀測值之間的差異，RMSE越小，預測結果越準確。MAE表示預測值和觀測值之間絕對誤差的平均值，可以更好地反映預測值誤差的實際情況，MAE越小，預測結果越好。從表2中可以得出，FOM2相較于FOM1、FOM3和FOM4，在1kHz下MAE降低了31%、25%和12%，RMSE降低了24%、11%和7%；在2kHz下MAE降低了24%、27%和7%，RMSE降低了22%、15%和4%；在4kHz下MAE降低了18%、?9%和?6%，RMSE降低了15%、?5%和?4%；在10kHz下MAE降低了15%、4%和9%，RMSE降低了9%、2%和5%。可以看出，除了4kHz外，FOM2在四種模型中誤差是最小的，即使在4kHz，FOM2的誤差也只是略大于FOM3和FOM4。

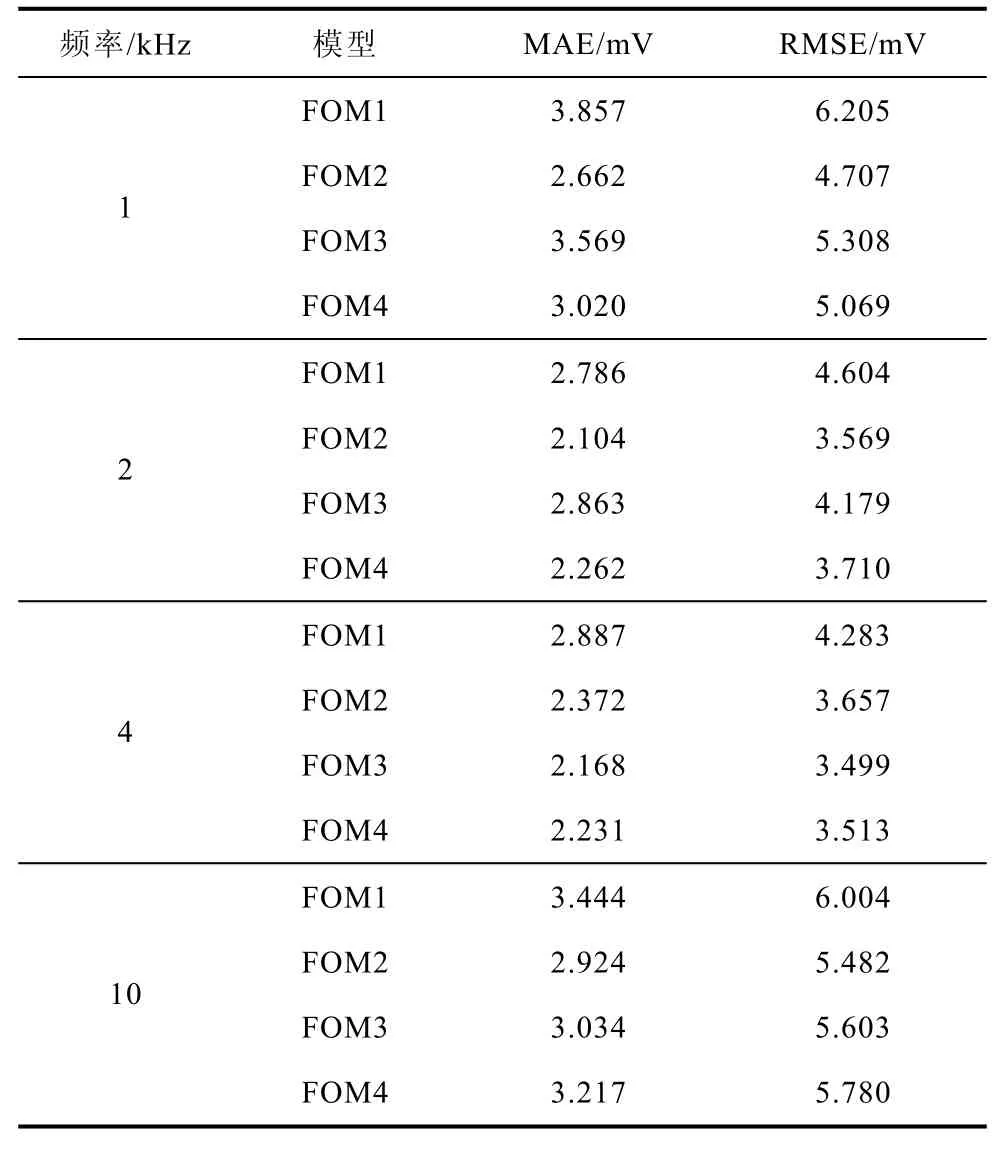
表2 不同模型的誤差 Tab.2 Errors of different models

3.2 計算量比較

分數階模型的計算量很大程度上取決于傳遞函數中分數階導數的數量，即與分數階元件的數量和位置有關。表3為不同模型的計算量。可以看出，FOM2和FOM3分數階導數個數最多，計算量最大，但由于總元件數不同，導致FOM3需要辨識的參數更多，計算量更大。同樣，FOM1與FOM4相比，FOM4計算量更大。四種模型的計算量從小到大依次為FOM1、FOM4、FOM2、FOM3，與實際仿真得到的結果相一致。

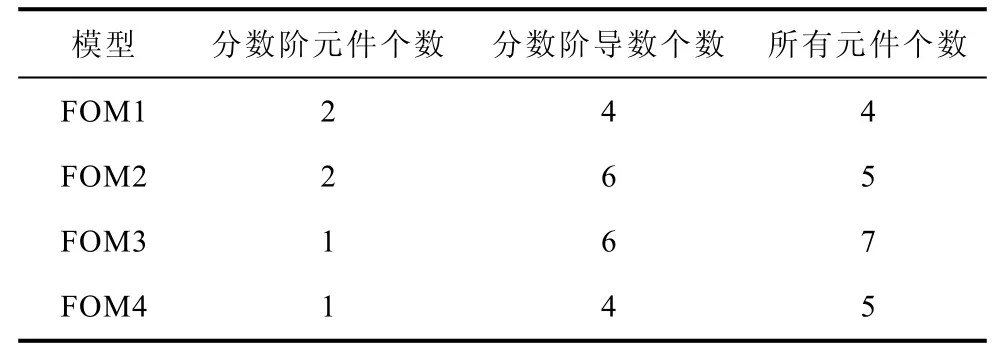
表3 不同模型的計算量 Tab.3 Computational load of different models

3.3 結果分析

從比較結果可以看出，根據應用領域的不同可以選擇不同的高頻模型，如果對模型精度要求較高時可以選擇FOM2，如果對運算速度要求較高時可以選擇FOM1。此外，從FOM2和FOM4的誤差比較中可以看出，二者的時域擬合結果相差并不大，但是EIS的擬合結果卻有較大差異，用FOM4對[1Hz, 20kHz]的EIS進行擬合后，擬合結果如圖10a所示，EFOM2=0.002 2，EFOM4=0.007 8。因此，在時域上對電池進行分數階建模時，不能忽略EIS與日常使用之間的差異。如果將EIS的測量頻率范圍增加到100kHz，則這種差異將變得更加明顯，四種模型的擬合結果如圖10b所示，EFOM1=0.005 5，EFOM2= 0.005 6，EFOM3=0.002 6，EFOM4=0.015 8。可以看出，只有FOM3擬合結果較好，其他三種模型都不能較好地跟隨阻抗的變化，這與第2節時域擬合的結果不同。因此，適用于EIS擬合的復雜模型并不一定在時域擬合中也是最優，在針對高頻部分進行建模時需要注意這種差異性。

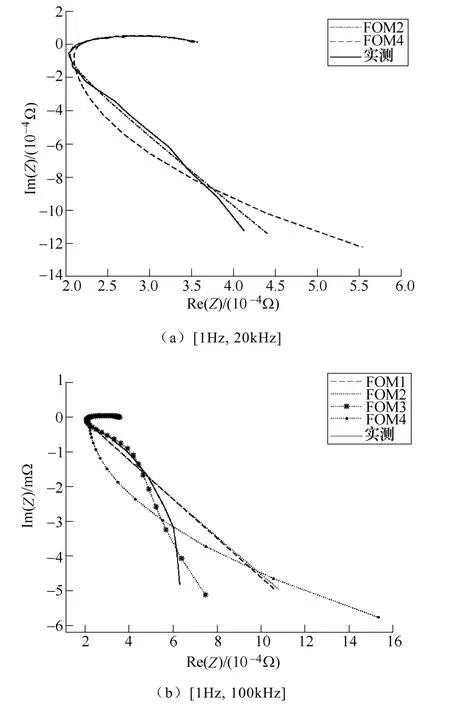
圖10 不同頻率范圍EIS擬合結果 Fig.10 EIS fitting results in different frequency ranges

4 結論

本文根據EIS的擬合結果選擇了三種分數階等效電路模型來模擬鋰離子電池在高頻紋波電流下的電壓響應，并由此設計了實驗，采集了鋰離子電池在不同頻率電流下的電壓響應。然后根據實驗數據對幾種模型進行了參數辨識，并根據辨識結果簡化了FOM2，提出了FOM4。最后從響應精度和計算量兩方面對幾種模型進行比較，其中FOM2的精度最高但是計算量較大，FOM1的計算量最小但是精度較低，根據應用領域和使用場景的不同可以進行不同的選擇。此外，從FOM2和FOM4的比較結果中還引申出另一個結論，即根據EIS擬合得到的復雜分數階模型并不一定在時域擬合中也能得到最優的結果。

本文只選擇了一種類型的電池進行了實驗，可以基于不同材料和類型的電池數據來擴展比較。此外，本文僅在短時間尺度下對模型進行了擬合驗證，將來可以對整個充放電循環進行驗證，并且估計鋰離子電池在高頻應力下的荷電狀態。