數控機床直線同步電動機磁懸浮系統反饋線性化控制的研究 *

孫云鵬 藍益鵬 徐澤來 雷 城

(沈陽工業大學電氣工程學院,遼寧 沈陽 110870)

驅動數控機床進給系統的磁懸浮直線同步電動機,因為導軌與進給工作臺之間無摩擦，具有速度和精度高，使用壽命長等優勢，被廣泛用于高速高精數控機床等領域[1]。然而由于可控勵磁直線磁懸浮同步電動機的氣隙磁場受勵磁電流與電樞電流之間的影響，存在著很強的電磁耦合，故對CELMSSM控制系統將產生不利影響。因此，如何提高磁懸浮系統控制系統的解耦效果和控制精度的分析與研究具有重要意義。

為了抑制耦合干擾，提高解耦效果，國內外學者對解耦控制系統進行了大量的研究[2-3],并在該領域取得了一定的成果。文獻[4]在傳統比例積分(proportional integral，PI)控制的基礎上，引入動態PI交叉解耦控制器，使系統對參數變化的敏感度降低，但由于多個控制器之前存在相互影響，將會增加控制器參數設計的難度。文獻[5-6]電流反饋解耦控制(current feedback decoupling control, CFDC)策略以及文獻[7-8]引入電流偏差解耦控制(current deviation decoupling control, CDDC)策略，即通過反饋電流和轉速對耦合部分進行計算并對交直軸電壓進行前饋補償，有利于提高系統的動態特性。但由于受參數變化的影響較大，因此該方法的穩定性還有待提高[9]。

反饋線性化控制(feedback linearization control, FLC)是一種非線性系統控制方法，在具有反饋線性化的仿射非線性系統得到應用[10]。該方法以微分幾何為基礎，通過求解解耦坐標變換矩陣和狀態反饋矩陣，使被控對象的非線性系統數學模型轉化為輸入量與輸出量之間呈線性關系的線性系統模型，從而實現非線性系統的解耦控制[11]。隨著FLC理論的不斷及發展，該控制方法迅速應用于異步電機混合勵磁同步電機等交流伺服系統中[12-13]。

為此，本文以CELMSSM傳統電流控制系統為基礎，根據非線性系統反饋線性化理論，得出了基于反饋線性化的電流解耦控制器，利用Matlab/Simulink平臺進行仿真，驗證了所提控制策略的可行性和有效性。

1 可控勵磁磁懸浮直線同步電動機的數學模型

可控勵磁直線磁懸浮同步電動機由動子和定子兩部分組成。動子由鐵心和三相交流繞組組成，定子由定子鐵心和直流勵磁繞組組成。CELMSSM結構如圖1所示。

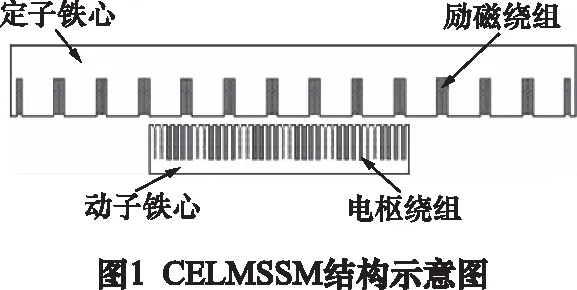
假設滿足以下條件：

(1)假設電機鐵心材料不飽和，不考慮渦流和磁滯帶來的影響。

(2)電樞繞組與勵磁繞組所產生的氣隙磁場正弦分布，忽略高次諧波影響。

(3)通入的電樞電流為三相對稱。

則在d-q坐標系下，可控勵磁直線同步電動機的數學模型由磁鏈方程，電壓方程等組成[14]。其中磁鏈方程為：

(1)

式中:ψd、ψq分別為電樞繞組直、交軸磁鏈，ψf為勵磁磁鏈；Ld為直軸電感，Ld=Lmd+Lσ；Lmd為直軸電樞反應電感；Lq為交軸電感，Lq=Lmq+Lσ；Lmq為交軸電樞反應電感，Lσ為電樞繞組漏感；Lf為勵磁繞組自感，Lf=Lmd+Lfσ；Lfσ為勵磁繞組漏感；id為電樞繞組直軸電流，iq為電樞繞組交軸電流，if為勵磁繞組電流。電壓方程為：

(2)

式中：ud、uq分別為電樞繞組直軸、交軸電壓，uf為勵磁繞組電壓；Rs為電樞繞組電阻，Rf為勵磁繞組電阻；v為直線電動機運行速度；為電機動子極距；f為電源供電頻率，v=2f。

電磁推力方程為：

(3)

式中：第二項(Ld-Lq)idiq是由凸極效應造成的磁阻變化在電樞反應磁場作用下產生的電磁推力。

懸浮力方程為：

(4)

水平方向運動方程：

(5)

垂直方向的運動方程：

(6)

式中：m是電動機的相數；N是電樞繞組每項串聯的匝數；kw1是電樞繞組的基波系數；bE是動子鐵心的有效寬度；p是極對數；δ為懸浮高度；Kc為卡特系數；Kd、Kq為直軸和交軸電樞反應系數，Kd=2.55×10-5，Kq=1.9×10-5；M為動子及負載質量；F1為水平方向上的負載阻力；Fdx為水平方向上齒槽效應、端部效應等不確定性擾動力的合力；Fdy為懸浮方向上的不確定性繞動力。

式(4)中，磁懸浮力產生很復雜，一是勵磁磁場對動子鐵心的吸引力。二是在垂直方向，由于通入直流和三相電后，兩個磁場會相互作用。三是電樞反應對定子磁軛的吸引力。

2 仿射非線性系統

考慮輸入多輸出系統(MIMO)中輸入輸出維數相等的系統，其一般表達式為：

(5)

式中：狀態變量x·Rn；輸入向量函數u·Rm；輸出向量函數y·Rm；f為n維充分光滑向量場，列向量gi(i=1，…，m)為Rn中光滑向量場；hi(i=1,…，m)是充分光滑的標量函數。

將單輸入單輸出系統(SISO)寫成仿射非線性的形式，有：

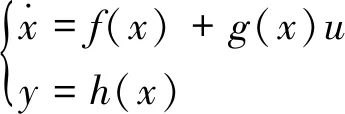
(6)

式中：x·Rn，u·R和y·R分別是系統的輸入和輸出，f(x)、g(x)是Rn上充分光滑的向量場。

對式(6)的系統輸出方程進行求導，表達式如式(7)所示：

(7)

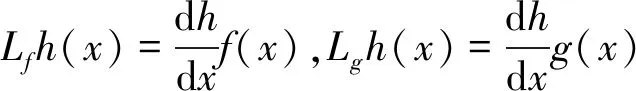
子系統相對階的求解公式如式(8)所示：

(8)

當相對階r等于系統階數n時，可以進行精確線性化，有式(9)所示的坐標變換：

(9)

對式(9)的每一項求導，有：

(10)

引入虛擬輸入量v，并令：

(11)

因此，原非線性系統可以線性化為式(12)所示的積分串聯的形式：

(12)

引入的虛擬輸入量v可以按照線性系統理論進行設計，由式(10)可解得系統的反饋控制律如式(13)所示。

(13)

3 數控機床直線同步電動機磁懸浮系統反饋線性化

由式(1)～(6)可得出CELMSSM數學模型的狀態方程為：

(14)

其中Ld=Lq，因此可將式(14)簡化為

(15)

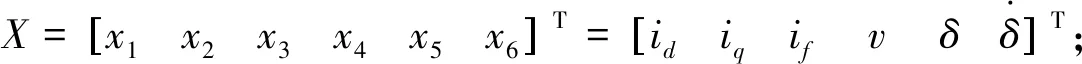
(16)

其中，

由f(X)的表達式可以看出動態數學模型中各參數之間存在耦合，這是造成系統非線性的主要原因。

由于該系統為三輸入三輸出系統，求該系統的相對階需要對id，v以及δ這3個輸出量分別進行求導。首先對id求導：

(17)

由于式中存在輸入量ud、uf，因此求導結束，相對階數r1=1。

對v進行求導，

(18)

由于式(18)不存才輸入量，因此需對v再次求導，可得

(19)

由于式中存在輸入量uq、uf，求導結束，相對階數r2=2。

同理對δ進行連續求導可得，

(20)

(21)

由于式中存在輸入量uq、uf，求導結束，相對階數r3=3。

其中，

因此系統總的相對階r=r1+r2+r3=6，系統的相對階等于系統的階數。因此，系統可實現狀態反饋線性化。

根據反饋線性化理論，尋找系統的標準型，對該系統進行坐標變換，選取新的狀態變量：

(22)

引入新的輸入變量：

(23)

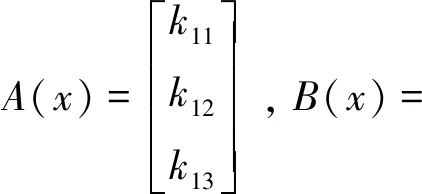
取輸入為：

(24)

原非線性系統變為：

(25)

狀態空間方程形式可表示為：

(26)

(27)

(28)

由式(26)～(28)可知，此時，輸出量與輸入量為線性2關系，原非線性動態解耦成直軸電流子系統、水平速度子系統以及懸浮高度子系統的3個獨立線性子系統，輸入c1、c2、c3分別獨立控制直軸電流id、水平速度v以及懸浮高度δ，系統變為線性能控系統。

4 基于最優極點配置的控制器設計

將式(24)代入式(16),有

(29)

再根據最優極點配置法設計c1、c2、c3。按照極點配置法c1、c2、c3是自定的反饋增益，為了使系統跟隨給定id*、v*、δ*，設e1=id*-id、e2=v*-v、e3=δ*-δ,選擇的反饋增益必須使得系統在原點穩定。

因而選取：

(30)

q1、q2、q3、q4、q5、q6為配置的反饋極點。當q1、q2、q3、q4、q5、q6均大于零時,將式(30)代入式(29)有

(31)

顯然可以根據勞斯判據驗證系統穩定。由公式可以看出，輸出id、v、δ受到給定id*、v*、δ*和e1、e2、e3的控制。

可控勵磁磁懸浮直線同步電動反饋線性化解耦控制框圖如圖2所示。

5仿真結果與分析

利用Matlab/Simulink建立CELMSSM仿真模型，對CELMSSM反饋線性化控制系統進行仿真研究，電機參數見表1。

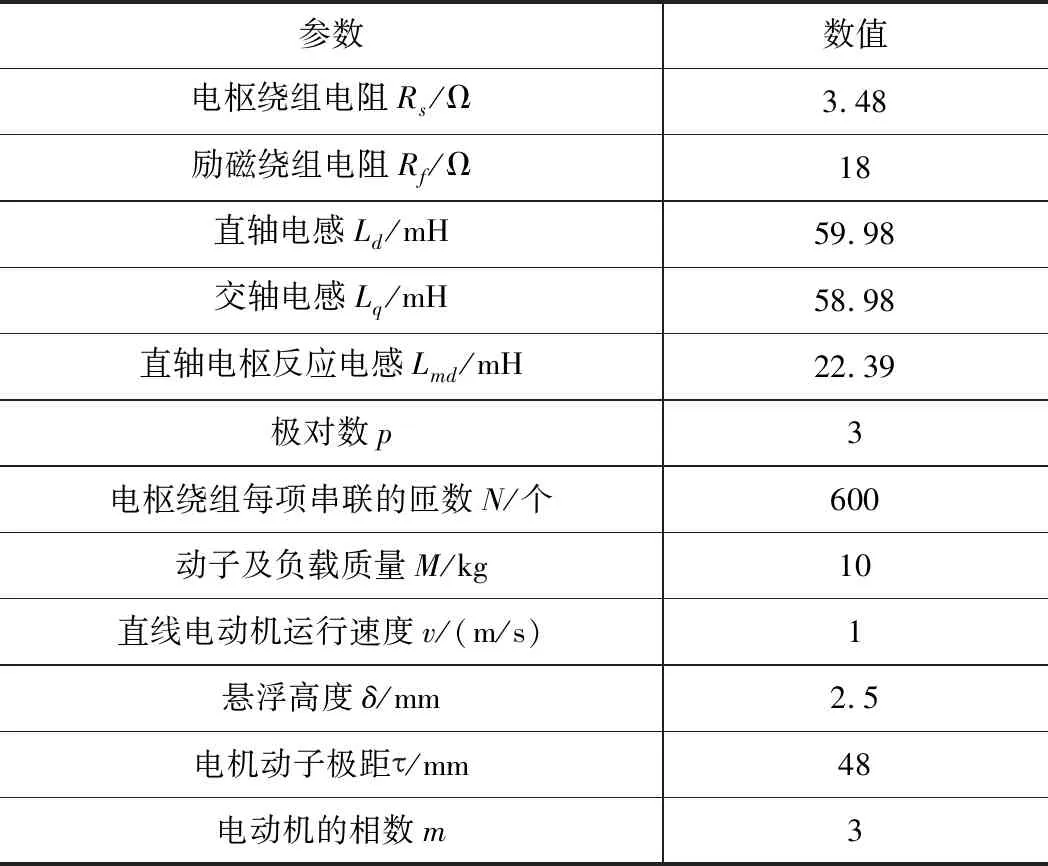
表1 電機參數

速度給定初始幅值為0 m/s，0.5 s發生階躍，階躍幅值為1 m/s；懸浮高度初始幅值為3 mm，給定值2.5 mm；給定d軸電流為0 A，空載啟動。當系統以1 m/s的速度穩定運行1.5 s時，在水平方向突加100 N的負載擾動，2.5～3 s時垂直方向突加40 N的負載擾動。由第4章式(29)、式(30)、式(31)和相關理論，再由經驗以及試湊法可得到極點配置參數[q1q2q3q4q5q6]=[4 10 24 18 62 192]。傳統PI控制系統與輸入輸出反饋線性化控制系統仿真結果如圖3～5所示。

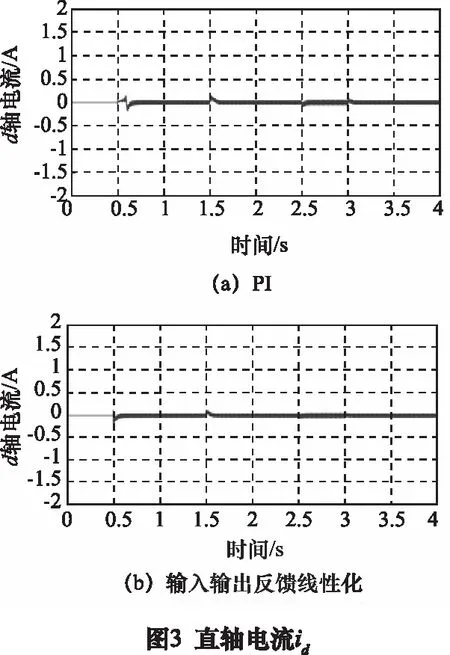
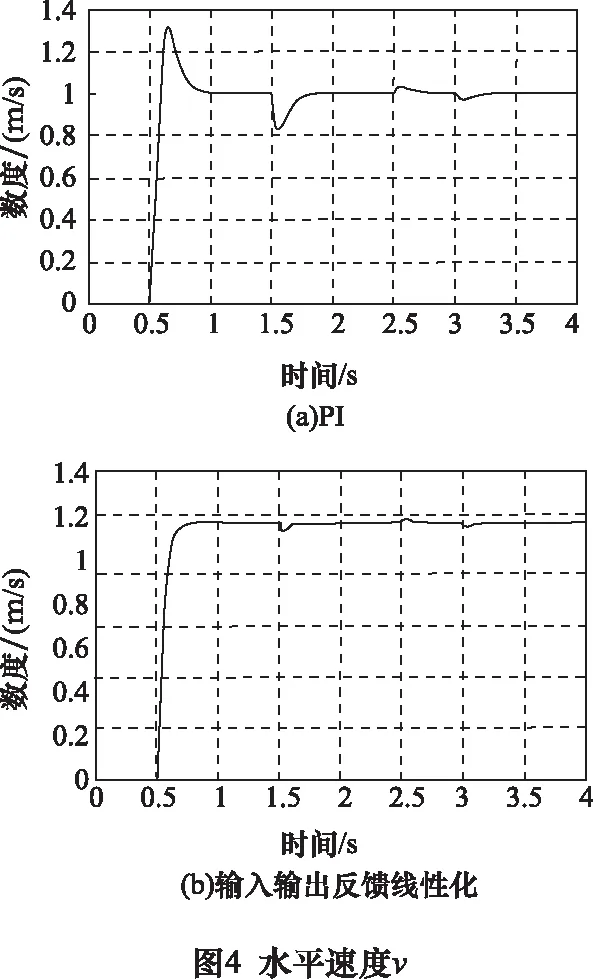
由圖3可知，輸入輸出線性化控制與傳統PI控制相比在啟動時，直軸電流震蕩較小，當施加負載擾動時電流波動較小。由圖4可知，水平方向上，輸入輸出線性化控制在啟動時，水平速度無超調，水平推力峰值較小，無震蕩，當施加負載擾動時速度和水平推力的變化較小，恢復時間更短。由圖5可知，在垂直方向上，輸入輸出線性化控制在啟動時，懸浮高度變化較小，當對系統突加負載擾動時，幅值變化小，懸浮力變化小。與傳統PI控制相比，當施加水平負載擾動時，懸浮高度變化更小；當施加垂直負載擾動時，速度變化更小，因此反饋線性化控制能夠減小系統耦合，提高系統控制性能。

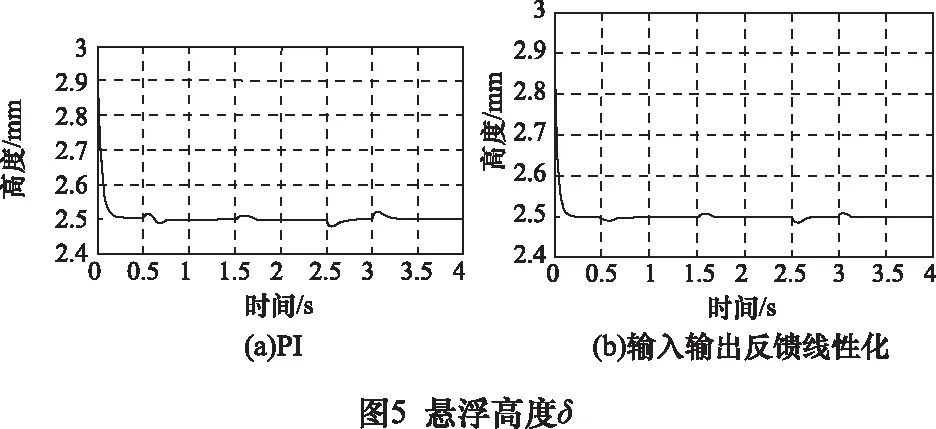
仿真是對電機在實際運行過程的模擬，例如，當系統以1 m/s的速度穩定運行，在1.5 s時在水平方向突加100 N的負載擾動，類似機床加工過程的進給過程，隨著進刀量的變化負載由0躍變到100 N。 垂直方向在2.5～3 s時突加40 N的負載擾動，用于模擬懸浮方向負載的變化過程。

6 結語

為了提高CELMSSM控制性能，保證系統的穩定性，對直軸電流id、水平速度v以及懸浮高度δ進行線性化，將原有的系統分成獨立的3個線性子系統，實現系統的反饋線性化。基于最優極點配置設計電流、速度和懸浮高度控制器。通過仿真實驗得出，在加入反饋線性化解耦控制器后，各輸出分量的抖動減小，靈敏性提高，系統的動、靜態性能得到顯著改善，仿真結果驗證了控制策略的有效性。