錦標賽精英學習與協方差變異的煙花算法
萬 達,李 俊
1.武漢科技大學 計算機科學與技術學院,武漢 430065
2.智能信息處理與實時工業系統湖北省重點實驗室,武漢 430065
受煙花在夜空爆炸這一自然現象啟發,Tan 等[1]于2010 年提出了煙花算法(FireWorks Algorithm,FWA),FWA 主要由爆炸算子、變異算子和選擇策略三大部分組成,其在解決單目標優化問題過程中,具有很好的效果。煙花算法自提出后就受到了諸多科研工作者的關注,許多改進算法也相繼被提出。煙花算法的改進主要可以分為兩類:一類是在基本煙花算法或其他改進煙花算法的基礎上進行算子的分析和改進;另一類是將煙花算法與其他啟發式算法結合。
第一類算法改進主要有:Zheng等[2]對煙花算法的爆炸算子、變異算子、選擇策略和映射規則等進行了詳細的分析,針對其存在的缺陷做出了五點改進,提出了增強型煙花算法(Enhanced FireWorks Algorithm,EFWA)。接著,Zheng等[3]和Li等[4]通過自適應調整核心煙花的爆炸半徑分別提出了動態搜索煙花算法(dynamic search FireWorks Algorithm,dynFWA)和自適應煙花算法(Adaptive FireWorks Algorithm,AFWA)。文獻[3]中,煙花爆炸半徑的變化過程由煙花種群產生的火花適應度值是否發生改進(即是否得到適應度值更優的火花)來決定。文獻[4]中,煙花爆炸半徑依據當前種群中最優個體與特殊個體間的距離自適應調節。這兩種方法由于采用了自適應調整爆炸半徑的機制,都極大提升了增強型煙花算法的性能。方柳平等[5]在dynFWA 基礎上,通過嵌入兩種利用歷史成功信息生成的不同的學習因子的方式來改進傳統的動態搜索煙花算法,提出了一種改進的動態搜索煙花算法(IdynFWA)。張水平等[6]在增強型煙花算法的基礎上,引入一種動態爆炸半徑調整機制,并在選擇過程中引入了一種雙精英-錦標賽選擇策略,提出了帶有動態爆炸半徑的增強型煙花算法(EFWA-DER)。Zheng 等[7]在dynFWA 基礎上,通過使用獨立選擇的方法顯著地提高了煙花的開采能力,并且在煙花之間加入避免擁擠的合作策略,提出了基于煙花算法的合作框架(CoFFWA)。之后,Zheng等[8]又將協方差變異算子引入到CoFFWA中,提出了基于協方差變異的協同框架煙花算法(CoFFWA-CM)。Li等[9]在煙花算法中引入引導火花,提出了引導煙花算法(GFWA)。Li等[10]針對解決多模式優化問題提出了一種基于淘汰者錦標賽的煙花算法(LoTFWA)。
第二類算法改進主要有:Zheng 等[11]提出了將煙花算法和差分演化算法進行混合的一種新型算法(FWADE)。黃輝先等[12]為解決多目標優化問題,用差分變異算子代替高斯變異算子,提出了進化信息引導的煙花差分混合多目標算法(MOHFWDE)。劉茜等[13]提出了一種由差分進化引導趨化算子的煙花算法(BFA),該算法在求解過程中利用優越火花的位置信息,通過差分進化算法驅動其他粒子移動,從而對群體中其他粒子位置信息進行改善,增強了粒子群體間的交流,削弱了映射規則和高斯變異給整個求解過程帶來的不良影響,提高了算法的優化性能。韓守飛等[14]將模擬退火的思想引入到煙花算法中,并對煙花算法中某些單個煙花個體進行高斯擾動,提出了一種基于模擬退火與高斯擾動的煙花優化算法(SAFWA)。莫海淼等[15]提出一種具有自適應步長與協同尋優的蝙蝠煙花混合算法。Zhang 等[16]提出了一種將生物地理學優化算法和增強型煙花算法(EFWA)進行混合的煙花算法(BBO-FWA)。Chen等[17]提出一種將煙花算子嵌入到粒子群算法求解過程中的全局優化混合算法(PS-FW),該算法在解決全局優化問題過程中具有良好效果。
文獻[10]使用了一種新的爆炸火花分布方式,以及提出了一種淘汰錦標賽策略,實驗證明該算法在解決多模式優化問題上具有較好的效果。但是該算法并沒有將最重要的核心煙花與其他煙花區分開來,進行進一步的操作,也沒有利用上一代煙花的信息。導致該算法全局探索能力較強,但是局部搜索效果并不明顯,算法收斂速度過慢。
針對文獻[10]中的不足,本文提出了一種基于錦標賽精英學習與協方差變異的煙花算法(GLFWA-CM)。首先,本文算法根據當代核心煙花相對于上一代核心煙花的變化來確定核心煙花在每一維上的爆炸半徑及其爆炸火花分布,加強了不同代煙花之間的信息交互,使得搜索資源的分配更加合理,提高了算法的局部搜索能力。其次,本文引入一種協方差變異算子,先計算部分適應度值較好的爆炸火花的均值和協方差,然后根據均值和協方差來隨機產生一個協方差變異火花,代替文獻[10]中的引導火花,有助于平衡算法的局部搜索和全局搜索能力。同時,本文提出了一種基于錦標賽的精英學習策略,對于選擇后的較差個體并沒有淘汰掉,而是讓它們向最好個體學習,提高了算法的收斂速度。最后通過15 個測試函數來驗證本文算法的有效性和準確性,并與其他算法的實驗結果進行比較。
1 煙花算法
在煙花算法中,為不失一般性,假設待求解的優化問題形式如下[18]:

其中Ω為解的可行域,使用煙花算法對優化問題(1)進行求解的目標是在可行域Ω內,尋找一點x,使得f(x)具有全局最小值。
假設煙花種群規模為N,煙花算法產生子代的方式是在N個煙花附近的規定區域內通過爆炸操作生成爆炸火花。對于煙花xi,其爆炸半徑Ai和爆炸火花數目Si的計算公式分別為:
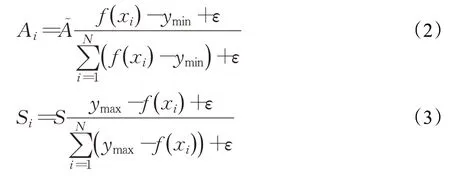
式(2)中,ymin為當前煙花種群中適應度最小值;式(3)中,ymax為當前煙花種群中適應度最大值。是常數,用來調整爆炸半徑大小,S也是個常數,用來調整產生的爆炸火花數目大小,ε是一個機器最小量,用來避免除零操作。
為了避免產生過多或者過少的火花,對于式(3)中的Si進行了如下的限制:
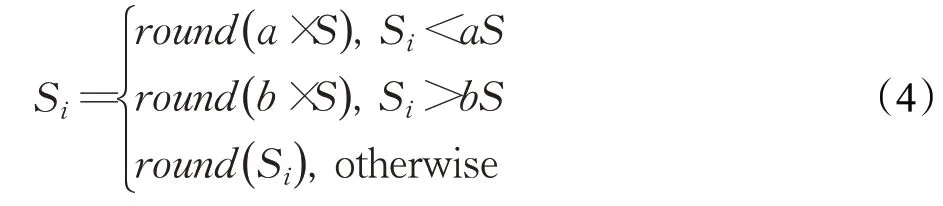
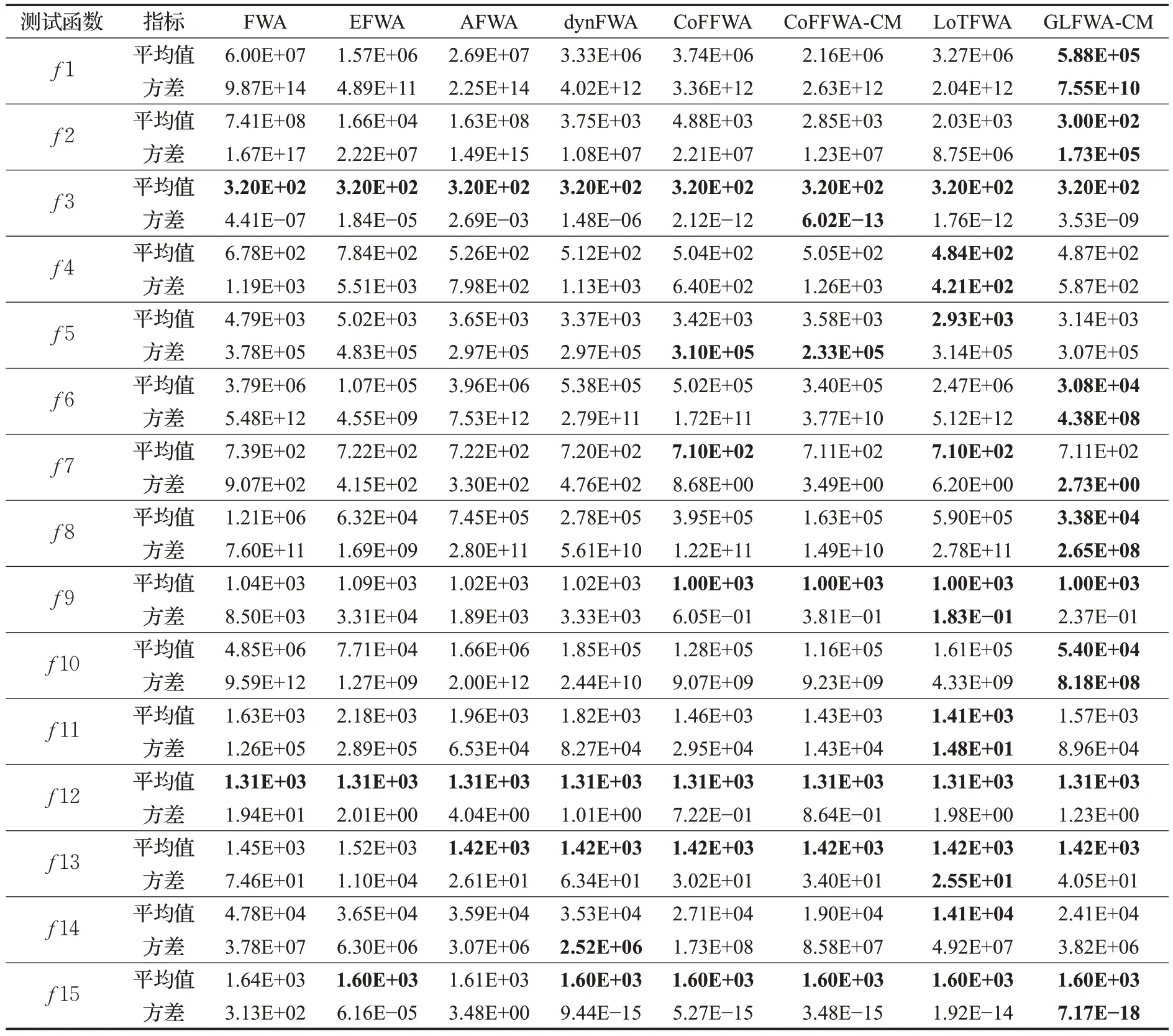
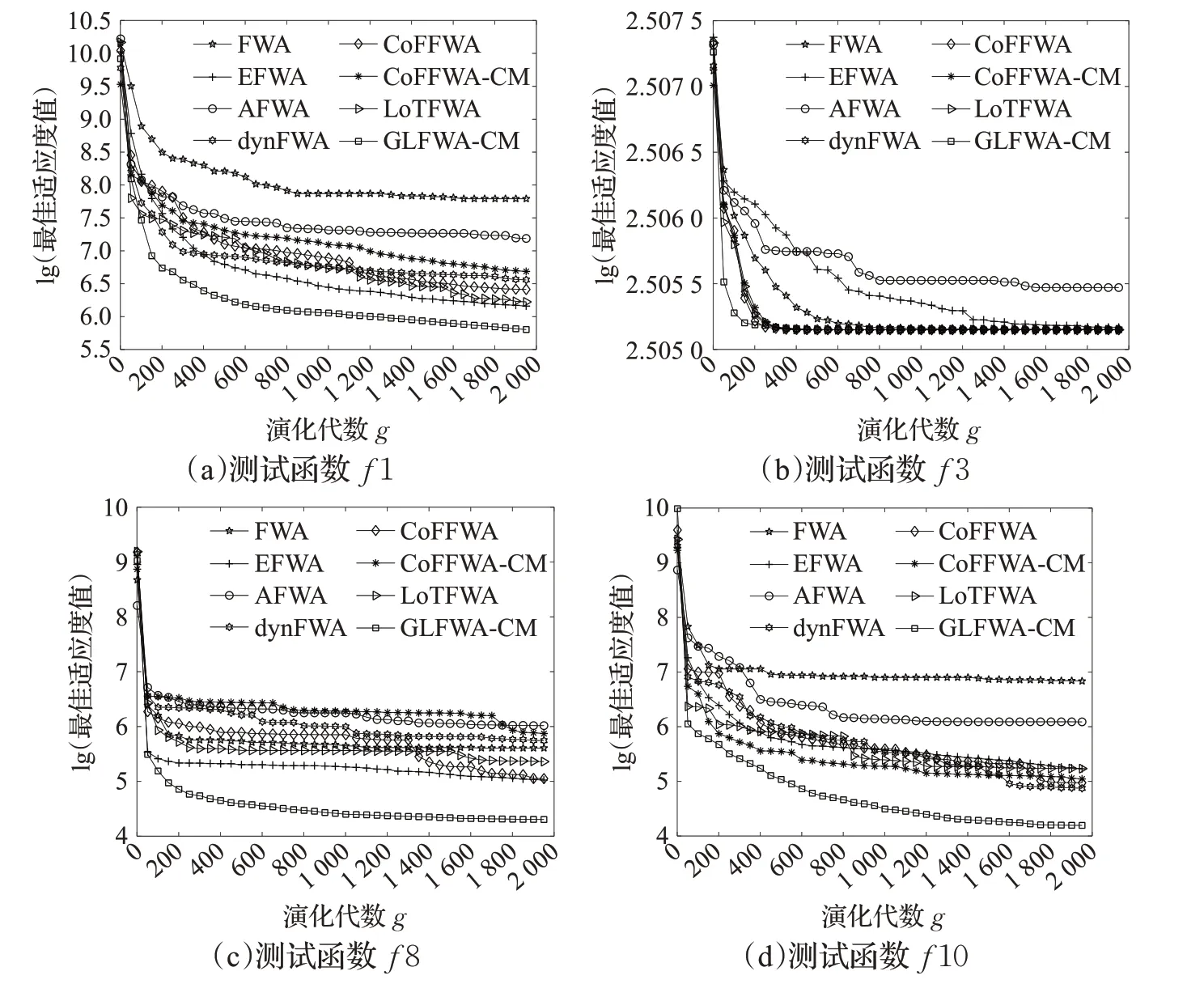
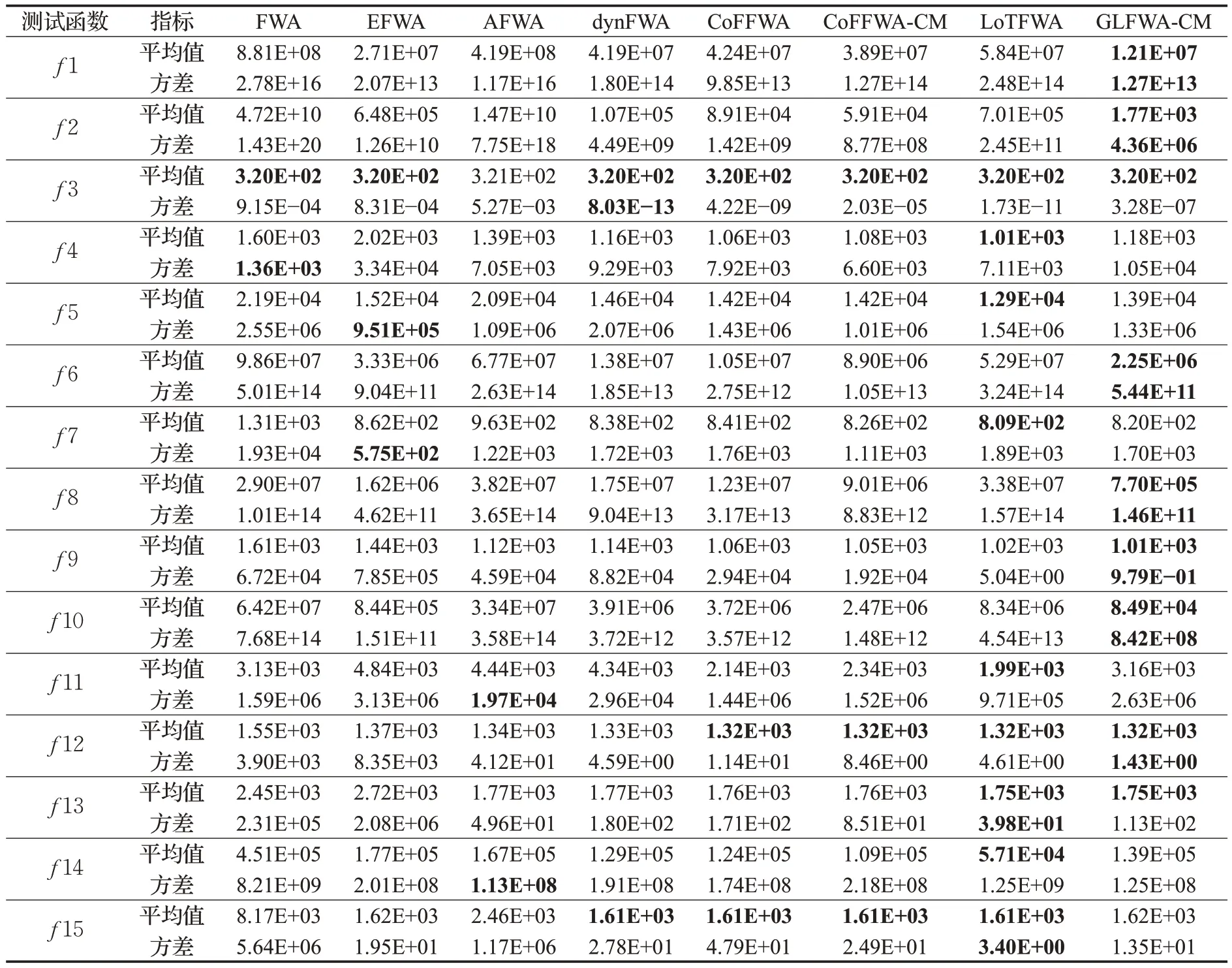
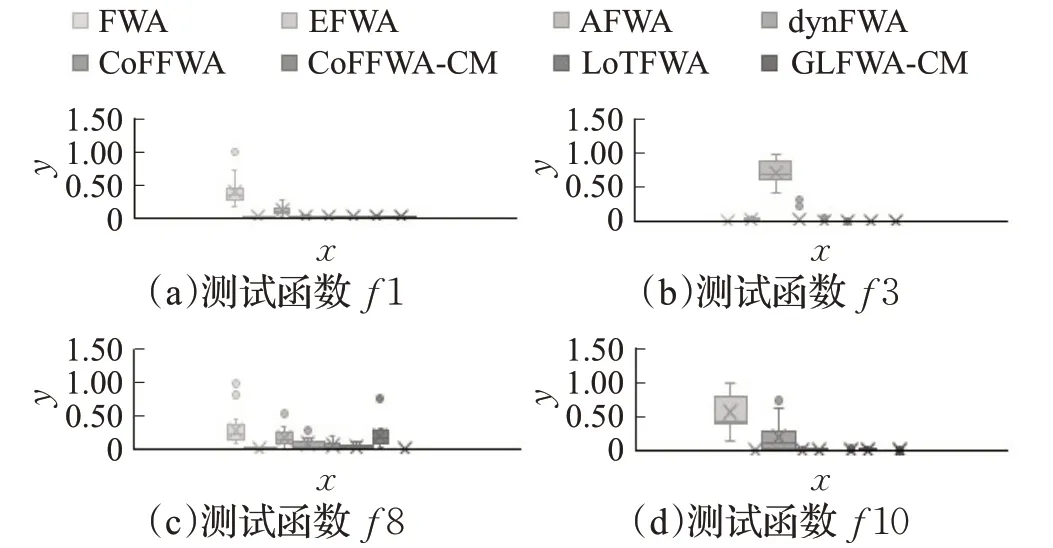
式(4)中,a、b是兩個常數,且a 在確定煙花的爆炸半徑和爆炸火花數目后,就可以執行爆炸操作了。第i個煙花xi產生第j個爆炸火花x(i,j)的方式為:從第i個煙花中隨機選擇z維坐標按下式更新: 式(5)中,k為被選擇的維度,Ai為第i個煙花的爆炸半徑,rand(-1,1)為區間[-1,1]之間的一個均勻隨機數。 為了增加煙花種群的多樣性,煙花算法引入了變異算子用于產生高斯變異火花。高斯變異火花產生的過程如下:首先在煙花種群中隨機選擇一個煙花xi,然后從該煙花所有維度坐標中隨機選擇z維坐標執行高斯變異操作,對煙花xi的第k維坐標執行高斯變異操作的公式為: 式(6)中,e~N(1,1),N(1,1)表示均值和方差均為1的高斯分布。 在產生爆炸火花和高斯變異火花的過程中,可能會出現產生的火花在可行域Ω的邊界以外的情況。當火花在維度k上超出邊界時,將通過下式將其映射到可行域Ω之內。 為使煙花種群中優秀的信息能夠傳遞到下一代種群中,算法會在候選者集合K(包括煙花、爆炸火花和高斯變異火花)中選擇N個個體作為下一代的煙花。候選者集合K中適應度值最小的個體會被確定性地選擇到下一代作為煙花,而對于剩下的N-1 個煙花的選擇采用輪盤賭的方法在候選者集合K中進行選擇。對于候選者xi,其被選擇的概率p(xi)計算公式如下: 式(8)(9)中,R(xi)為當前個體到候選者集合K中除xi外所有個體之間的距離之和。 針對傳統煙花算法收斂精度低,收斂速度慢,容易陷入局部最優等問題,提出一種基于錦標賽精英學習與協方差變異的煙花算法(GLFWA-CM)。該算法主要包括爆炸算子、協方差變異算子和選擇策略三個部分。在爆炸算子中,用冪律分配的方式來計算爆炸火花數目,根據煙花是否產生更好的火花來動態確定爆炸半徑,如果產生更好的火花,則增大爆炸半徑,否則減小,這兩種策略可以有效解決煙花算法容易陷入局部最優的問題。同時,根據核心煙花更新信息來確定核心煙花每一維的爆炸半徑,并且在更新方向上產生更多火花,這種方法顯著增強了核心煙花的局部探索能力,提高了算法的收斂精度。對超出邊界的火花使用一種隨機映射規則,避免了煙花算法火花往往映射在原點附近的缺陷。用協方差變異火花代替其他變異火花,可以有效平衡算法的局部搜索和全局搜索能力。對于獨立選擇后的較差煙花,執行一種基于錦標賽的精英學習策略,可以有效提高算法的收斂速度。 本文根據煙花適應度值的優劣將煙花分成了核心煙花和非核心煙花,其中核心煙花xF是煙花種群中適應度值最優的煙花,除核心煙花外,其他的都是非核心煙花。 2.1.1 冪律分布 冪律分布[19]是指某個具有分布性質的變量,且其分布密度函數是冪函數的分布。在煙花算法中,爆炸火花的數目僅僅與煙花的適應度值有關,當煙花較差時,其爆炸火花數目往往只能取最小閾值,而這類煙花爆炸半徑又相對非常大,所以這類煙花搜索效率極低,這顯然不合理。為了改變這種不合理現象,本文采用一種冪律分配的方式來計算爆炸火花數目。首先是對煙花適應度值進行升序排序,并確定煙花的等級,其中,適應度值越小,等級越低。然后,根據煙花的等級計算爆炸火花的數目,計算方法如下: 式(10)中,Si指第i個煙花的爆炸火花數目,S為常數,用來調整產生的爆炸火花數目大小,N為煙花種群規模大小,ri表示煙花xi的等級,α是一個常數。從式(10)可以看出爆炸火花數目的分配與該煙花適應度值的排序相關聯,而不再像式(3)那樣依賴適應度值的數值本身。文獻[10]證明了這是一種很有效的資源分配方式。 2.1.2 動態爆炸半徑 在煙花算法中,爆炸半徑是根據式(2)計算的,分析式(2)可知,當煙花之間適應度值相差較大時,適應度值較小的煙花其爆炸半徑也相對較小,假設在該煙花搜索區域存在一個局部最優解,那么在迭代過程中,該區域煙花爆炸半徑會不斷縮小,爆炸火花數目會不斷增加,并且由于它占據大量資源,導致其他煙花搜索資源減少,降低了找到全局最優解的概率。那么最終算法很可能就會陷入局部收斂,并且很難跳出。 為了避免這種情況,本文引入一種動態爆炸半徑策略。煙花算法的爆炸半徑根據上一代最優解自適應地改變,當煙花產生適應度值更好的火花時,煙花爆炸半徑會增大以提高全局探索能力,再加上2.1.1 小節提出的爆炸火花冪律分配方式,使得煙花之間的爆炸火花數目不會相差太懸殊,該策略可以有效解決煙花算法容易陷入成熟收斂的問題。本文煙花爆炸半徑的計算公式如下: 2.1.3 核心煙花更新信息引導 在煙花算法中,核心煙花的爆炸半徑對煙花算法的性能有著決定性的影響。而大家知道,在算法迭代過程中,尤其是在前期,核心煙花一直在更新,這種更新表明了煙花算法向著最優解方向搜索的趨勢。那么,在潛在最優解位置明確的情況下,可以利用這種趨勢,即利用核心煙花的更新信息來確定核心煙花在不同維度的爆炸半徑以及其爆炸火花的分布。基本思想是核心煙花在更新幅度越大的維度其爆炸半徑就越大,反之,則越小。另外,在爆炸過程中,朝著核心煙花的更新方向上分布更多的火花。這樣有助于核心煙花在更新方向上進行更加細致的搜索,增加了核心煙花找到最優解的概率。但同時需要注意的是,雖然更新信息指出了潛在最優解的位置,但是也存在著最優解不在更新方向上的可能性。如果所有的火花或太多的火花都分布在更新方向上,則算法很有可能會陷入局部最優。因此,在選擇某一維度執行爆炸操作時,需要確定一個合適的選擇概率β,以確保大多數火花分布在更新方向上,也要保證有一定火花分布在更新方向的反方向上,具體實現方法在算法1中給出。 算法1 上述操作的實質是在核心煙花的更新方向上,增加爆炸火花的數目,而在其他方向上,減少爆炸火花數目。這雖然顯著增強了核心煙花尋找最優解的能力,但是也對核心煙花爆炸火花的多樣性有一定影響,增加了算法陷入局部最優解的可能性。為了降低該策略對算法全局探索能力的影響,本文中最大爆炸火花數目設置的相對較大,通過產生更多的爆炸火花,一定程度上彌補了這些方向的火花喪失,可以進一步降低該策略對火花多樣性的影響。同時爆炸火花數目的增多,也使得核心煙花可以更加細致地在更新方向上進行局部搜索,提高算法收斂精度。 對于核心煙花,其各個維度上的爆炸半徑的計算公式如下: 式(12)中,xF(g)和xF(g-1) 分別是當前代和上一代核心煙花,而ΔxF則是當前代核心煙花的更新信息。在式(13)中,|ΔxF(k) |是核心煙花更新信息在第k(k=1,2,…,D)維上的絕對值,D是維數,是根據式(11)計算的當前核心煙花所在小組的動態爆炸半徑,(g)是當前代核心煙花在第k維上的爆炸半徑,ε是一個機器最小量,用來避免除零操作。 根據式(12)可知,當核心煙花的信息在某一維并沒有更新或者更新幅度很小時,|ΔxF(k) |接近于0,而不等于0,那么,(g)也接近于0,即當前代核心煙花在第k維上的爆炸半徑接近于零,這顯然不利于核心煙花在該維空間上的搜索,為了避免這種情況,本文采用了一種最小爆炸半徑檢查操作,具體計算公式如下: 在式(14)中,Ainit和Afinal是最初和最終的最小爆炸半徑,evalsmax是最大函數評估次數,t(t=1,2,…,evalsmax)是指當前的函數評估次數,(t)是在評估次數為t時第k維的最小爆炸半徑。 2.1.4 隨機映射規則 在式(7)的映射規則中,存在一個問題。在一般情況下,解空間往往是關于原點O對稱分布的,而且超出解空間邊界的火花往往分布在解空間邊界附近,這就造成這些火花在使用公式(7)映射時,往往映射在原點附近,這無形中造成了搜索資源的浪費,也容易促使煙花算法陷入局部最優。為了解決這個問題,本文采用了一種隨機映射規則,具體映射公式如下: 文獻[2]對FWA經過分析后指出煙花算法的高斯變異公式存在缺陷,當產生的隨機數e接近或等于0時,產生的變異火花就會分布在原點附近,并且很難跳出。因此,文獻[2]提出了一種改進的高斯變異算子。之后,文獻[20]又提出了一種新的變異算子,被稱為協方差變異算子。相較于EFWA[2]僅僅利用每一代核心煙花的信息,FWA-CM[20]利用了煙花產生的部分適應度值最好的爆炸火花的信息,在更可能找到最優解的方向產生變異火花。實驗證明協方差變異不僅可以避免FWA中變異公式的缺陷,而且相比EFWA 中的變異方式,協方差變異在更可能找到最優解的方向產生變異火花,提高了算法找到最優解的概率。并且由于協方差變異火花是利用爆炸火花的信息產生的,所以一般分布在煙花附近,這樣對平衡算法整體的探索和開發能力也是有幫助的。因此,本文也使用協方差變異算子來產生變異火花,具體操作步驟如下: 首先,假設煙花產生的爆炸火花數目為λ,從所有的爆炸火花λ中選取適應值最好的μ個火花,m為被選中的μ個火花的均值,其計算方法如下: 式(17)中,xi為被選中的第i(i=1,2,…,μ)個火花。 在求得這μ個火花的均值m后,還需要計算這μ個火花數據的協方差矩陣,其協方差矩陣C的計算方法如下: 式中,ai和bi為第i個火花在d1和d2維度上的值,、為這μ個火花在d1和d2兩個不同維度上的均值。需要注意的是,分母是μ,而不是協方差計算公式的μ-1,C是一個D×D的矩陣。 在選擇新一代煙花時,GLFWA-CM 采用了獨立選擇策略和基于錦標賽的精英學習策略。獨立選擇策略是指將每個煙花和各自產生的火花看作一組,在進行煙花選擇時,直接從每組里選擇適應度值最好的個體作為下一代的煙花。文獻[7]證明這種方式可以確保把當代每個煙花的搜索經驗傳遞給下一代,而且每個煙花在各自區域的獨立搜索也增加了非核心煙花對于優化過程的貢獻度。 獨立選擇策略使得算法能夠保持完整的探索能力,但是搜索資源始終是有限的,為了解決煙花算法收斂速度慢的問題,提出一種先競爭后學習的方法。煙花個體之間通過自身預估的最終適應度值進行競爭,如果某個被選擇的個體不能在自身適應度值的基礎上以當前的進化速度追趕上當代最好的個體,就會通過學習的方式來靠近當代最好個體,這樣可以進一步增強算法在核心煙花附近的局部探索能力,并且加快算法的收斂速度。另外,在迭代過程中,由于獨立選擇策略,某些非核心煙花有可能在自己的搜索區域附近陷入局部最優,此時,它們的爆炸半徑會不斷減小,與核心煙花的差距也越來越大,當大到某種程度時,就會向核心煙花靠近,在靠近過程中逐漸找到更優解,爆炸半徑會逐漸增大,最終幫助其跳脫出局部最優。如算法2所示,是基于錦標賽的精英學習策略的偽代碼: 算法2 在算法2中,是使用獨立選擇策略從每個組(包括煙花和其產生的所有火花)里預選出來的第i(i=1,2,…,N)個煙花,是被選擇的煙花中適應度值最好的煙花,是爆炸前的第i個煙花,f()是求解適應度值函數,g是當前迭代次數,Gmax是最大迭代次數,γ是一個常數參數。 GLFWA-CM算法的具體實現步驟如下: 步驟1初始化煙花種群規模N,協方差變異火花數目M,最大爆炸火花數目S,最大演化代數Gmax,爆炸火花數目分布參數α,選擇概率β,精英學習因子γ,動態爆炸半徑增大系數Ca和減小系數Cr,協方差變異火花選擇比率η/λ,解的可行域Ω的上下邊界和,初始爆炸半徑,初始最小爆炸半徑Ainit和最終最小爆炸半徑Afinal等參數。 步驟2初始化N個煙花位置,并計算它們的適應度值,找出核心煙花xF。 步驟3根據適應度值大小對煙花進行排序,并劃分等級,適應度值越小,等級越低。 步驟4根據式(10)計算每個煙花的爆炸火花數目Si。 步驟5根據式(11)計算煙花的爆炸半徑。 步驟6根據式(12)~(15)計算核心煙花在每一維上的的爆炸半徑(g)。 步驟7核心煙花根據算法1產生爆炸火花。 步驟8非核心煙花根據式(5)產生爆炸火花。 步驟9根據式(16)將超出可行域的火花映射到可行域內。 步驟10根據式(17)和(18)分別計算被選擇火花的均值m和協方差矩陣C,根據N(m,C)隨機產生一個協方差變異火花。 步驟11從每組煙花及其產生的所有火花中預選出適應度值最優的個體。 步驟12從預選擇的煙花種群中找出適應度值最優的個體。 步驟13根據算法2對預選擇的個體進行錦標賽精英學習操作。 步驟14判斷是否滿足終止條件,若滿足,則返回全局最優解及其適應度值;否則,返回步驟3 進行循環迭代。 GLFWA-CM 算法的各項參數設置:煙花種群規模N=5,協方差變異火花數目M=5,最大爆炸火花數目S=200,最大演化代數Gmax=2 000,爆炸火花數目分布參數α=3,選擇概率β=0.7,精英學習因子γ=0.1,動態爆炸半徑增大系數Ca=1.2,減小系數Cr=0.9,協方差變異火花選擇比率η/λ=0.25,解的可行域Ω的范圍為[-100,100],,煙花初始爆炸半徑,初始最小爆炸半徑,最終最小爆炸半徑 為了全面客觀地對GLFWA-CM 算法進行評價,本文將其與標準煙花算法FWA[1]以及近些年提出的一些改進煙花算法EFWA[2]、AFWA[4]、dynFWA[3]、CoFFWA[7]、CoFFWA-CM[8]、LoTFWA[10](α和λ參數分別設置為3和200)在收斂精度、收斂速度和穩定性上進行比較,其他比較算法的參數設置均與原文獻一致。每個算法均獨立運行20次,算法問題維度D=30/100,每個測試函數的最大評估次數evalsmax=10 000。實驗環境為:處理器Intel?Core?I5 6200U @ 2.30 GHz,RAM 4 GB,Win10 64位操作系統,MATLAB R2018b。 為了驗證本文算法的適用性、有效性和正確性,選擇CEC2015[21]中的15個標準測試函數,具體定義如表1所示,其中f1、f2 為單峰函數,f3~f5 為簡單多峰函數,f6~f8 為混合函數,f9~f15 為復合函數。 表1 CEC2015的15個Benchmark函數Table 1 15 Benchmark functions of CEC2015 3.3.1 收斂性分析 文獻[22]給出了煙花算法的馬爾可夫過程收斂到最佳狀態的充分條件,本文在此充分條件的基礎上對GLFWA-CM算法的收斂性進行證明。 GLFWA-CM算法將煙花和各自產生的火花分為一組,選擇時直接選擇每組中最好的個體作為下一代煙花。每個被選擇的煙花都繼承了該組的搜索經驗,能夠不斷在其附近區域進行探索,而不會突然跑到距離很遠的區域去重新搜索,提高了搜索的效率。協方差變異在該組煙花搜索區域附近產生一個靠近更優解的火花,提升了每個小組找到最優解的概率。當產生的火花比煙花更好時,由于動態爆炸半徑機制,煙花的爆炸半徑會增大,這樣使得算法前期有強大的全局探索能力。隨著迭代過程的進行,每組煙花的搜索區域開發的越來越完善,找到的解也越來越好,某些煙花甚至已經找到自己搜索區域附近的局部最優解,陷入局部最優的狀況。到了迭代后期,一些陷入局部最優或者進化速度太慢的非核心煙花,由于找到更優解的概率很低,那么就會在錦標賽精英學習策略的引導下,向找到更優解的核心煙花靠近,提高了核心煙花附近的搜索密度。由于核心煙花附近找到全局最優解的概率最大,所以GLFWA-CM 算法后期的開發能力很強。核心煙花在核心煙花更新信息的引導下,向著更有可能找到最優解的方向搜索,又進一步增加了算法找到全局最優解的概率。綜合分析可知,GLFWA-CM算法前期探索能力不俗,后期開發能力很強。 表2 為各算法的實驗結果在30 維情況下的平均值和方差對比,其中最好結果已加粗標出。從平均值指標來看,對于f1、f2、f6、f8、f10 測試函數,GLFWA-CM算法要優于參與比較的其他算法,而且比它們都至少要好1~2個數量級。對于f3、f9、f12、f13、f15 測試函數,GLFWA-CM 算法與其他算法性能持平。對于剩下的其他函數,GLFWA-CM 算法結果與最好結果基本都在同一個數量級。從方差指標來看,對于f1、f2、f6、f7、f8、f10、f15 測試函數,GLFWA-CM算法要優于參與比較的其他算法。綜合來看,在低維條件下,GLFWACM和LoTFWA算法總體上優于其他算法,GLFWA-CM在單峰函數和混合函數上具有顯著優勢,LoTFWA在簡單多峰函數和部分復合函數上具有一定優勢。 表2 GLFWA-CM與其他算法的比較(D=30)Table 2 Comparison of GLFWA-CM with other algorithms(D=30) 圖1(a)~(d)展示的是各算法在低維(D=30)情況下的收斂過程。其中,f1 函數是單峰函數,從收斂曲線圖中可以看出,在迭代次數相同的情況下,與其他算法相比,GLFWA-CM算法收斂精度更高,而且它還有繼續收斂的趨勢;f3 函數是簡單多峰函數,從收斂曲線圖中可以看出,GLFWA-CM 算法收斂速度更快;f8 函數是混合函數,從收斂曲線圖中可以看出,GLFWA-CM算法收斂精度相比于其他算法具有明顯優勢;f10 函數是復合函數,從收斂曲線圖中可以看出,與其他算法相比,GLFWA-CM算法前期收斂速度與其他算法相當,后期,在其他算法收斂曲線趨于平緩時,GLFWA-CM 算法仍在緩慢收斂,而且收斂精度更高。綜合來看,在低維情況下,GLFWA-CM 算法在收斂精度和收斂速度上都具有一定優勢。 圖1 8種算法求解測試函數f 1、f 3、f 8、f 10 的收斂曲線(D=30)Fig.1 Convergence curves of test functions f 1、f 3、f 8、f 10 solved by eight algorithms(D=30) 表3為各算法的實驗結果在D=100 維條件下的平均值和方差的對比,其中最好數據已加粗顯示。從表3中數據可以看出,在D=100 時,GLFWA-CM 算法在單峰函數,混合函數f6、f8 以及復合函數f9、f10、f12、f13 上均獲得最優結果,在多峰函數和其他復合函數上也與最優結果相差不大。這說明GLFWA-CM算法解決高維問題時相較于對比的其他算法仍然有一定優勢,體現了GLFWA-CM算法具有很強的適應性。對于多種不同類別和不同維度的問題都有很好的尋優能力。 圖2(a)~(d)展示的是各算法在高維(D=100)情況下的收斂過程。從收斂曲線圖中可以看出,在迭代次數相同的情況下,與其他算法相比,對于f1函數,GLFWACM 算法收斂精度更高;對于f3 函數,GLFWA-CM 算法收斂精度與其他算法相當,但是前期收斂速度明顯更快;對于f8 和f10 函數,GLFWA-CM算法收斂精度相比于其他算法具有明顯優勢,在迭代后期,GLFWA-CM算法收斂速度也快于其他算法。說明在高維情況下,GLFWA-CM算法在收斂精度和收斂速度上仍然具有一定優勢。 圖2 8種算法求解測試函數f 1、f 3、f 8、f 10 的收斂曲線(D=100)Fig.2 Convergence curves of test functions f 1、f 3、f 8、f 10 solved by eight algorithms(D=100) 綜合分析表2 和表3,GLFWA-CM 算法在單峰函數、混合函數和部分復合函數上效果很好,在多峰函數和部分復合函數上僅次于LoTFWA。 表3 GLFWA-CM與其他算法的比較(D=100)Table 3 Comparison of GLFWA-CM with other algorithms(D=100) 這主要是因為核心煙花更新信息引導策略和協方差變異方法都是在更可能找到最優解的方向產生火花,增大了算法找到最優解的概率,基于錦標賽的精英學習策略使得較差的煙花向核心煙花附近移動,進一步提高了核心煙花附近區域的搜索密度。所以在單峰函數和混合函數上,GLFWA-CM 算法優勢顯著。由于核心煙花更新信息引導策略對爆炸火花的多樣性產生了一定影響,還有基于錦標賽的精英學習策略雖然顯著加快了算法的收斂速度,但也犧牲了一定的探索能力,使得GLFWA-CM算法在多峰函數和部分復合函數這類看重全局探索能力的問題上,效果不如LoTFWA。但是由于GLFWA-CM算法采用了一種與LoTFWA相同的動態爆炸半徑機制,能夠有效避免GLFWA-CM 算法陷入成熟收斂,所以其結果也僅僅比LoTFWA 稍差,與其他煙花算法持平。 綜合分析圖1和圖2,GLFWA-CM算法前期收斂速度最快,收斂精度最高,在迭代后期,GLFWA-CM 算法仍在緩慢收斂,而且收斂速度比其他算法更快。 這主要是因為核心煙花更新信息引導策略使得算法在更可能找到最優解的方向產生爆炸火花,提高了算法的收斂精度,基于錦標賽的精英學習策略使得較差的煙花向核心煙花附近移動,加快了算法向著最優解區域收斂的速度。所以在迭代前期,GLFWA-CM 算法無論是收斂速度還是收斂精度都是最好的。當算法找到一個局部最優解時,由于動態爆炸半徑機制的作用,非核心煙花的爆炸半徑會逐漸增大,擴大搜索區域,幫助算法跳出局部收斂,一旦找到更優解,其他煙花在錦標賽精英學習策略的引導下,也能逐漸跳出該區域,并能以較快的速度前往下一個核心煙花附近搜索,所以在迭代后期,算法仍能以較快的速度繼續收斂。 3.3.2 穩定性分析 一般來說,在理論上能確保收斂的算法具有較高的穩定性。本文3.3.1 小節已對GLFWA-CM 算法的收斂性進行了證明,本文算法穩定性主要是通過李雅普諾夫穩定性理論[23]來分析的。 平衡狀態:設某系統動態方程為: 式中,x為n維狀態向量,且顯含時間變量t,f(x,t)為線性或非線性,定常或時變的n維函數。對于所有t,滿足 的狀態xe稱為平衡狀態。平衡狀態的各分量相對于時間不再發生變化。若已知狀態方程,令X=0 所求得的解x,便是平衡狀態。 李雅普諾夫意義下的穩定性: 設系統初始狀態位于以平衡狀態xe為球心,r為半徑的閉球域S(r)內,即 若能使系統方程的解x(t:x0,t0) 在t→∞的過程中,都位于以xe為球心,任意規定的半徑為ε的閉球域S(ε)內,即 則稱系統的平衡狀態xe在李雅普諾夫意義下是穩定的。 實數r與ε有關,通常也與t0有關,如果r與t0無關,則稱平衡狀態是一致穩定的。 漸近穩定性: 若系統的平衡狀態xe不僅具有李雅普諾夫意義下的穩定性,且有: 則稱此平衡狀態是漸近穩定的。 證明GLFWA-CM算法平衡狀態是一致漸進穩定的 由于GLFWA-CM 算法收斂,且最終會收斂于全局最優點xbest,根據文獻[24]的證明,同理可證得全局最優點xbest為GLFWA-CM 算法在李雅普諾夫意義下的平衡點,f(xbest,t)為平衡狀態。 設GLFWA-CM 算法的初始狀態位于以平衡狀態xbest為圓心,r為半徑的圓S(r)內,圓S(ε)是以xbest為圓心,ε為半徑的圓,圓S(ε) 與f(x) 相交于x3、x4,Dbest為最優區域,最兩邊的點為x1、x2,滿足: 由GLFWA-CM 算法的收斂性可得當xi位于Dbest區域時,xi只會向著xbest靠近而不會遠離。因此只要方程的初始解x(t0:x0,t0)位于Dbest區域內,即圓S(r)與目標函數相交的區域包含于Dbest區域,方程的解x(t:x0,t0)就只會向著xbest靠近而不會逃出半徑為r的圓S(r),即 所以系統方程的解x(t:x0,t0)在t→∞的過程中,都位于以xbest為球心、任意規定的半徑為ε的圓S(ε)內,因此當圓S(r)與目標函數相交的區域包含于Dbest區域時,即滿足公式(26),GLFWA-CM算法的平衡狀態xbest在李雅普諾夫意義下是穩定的。 所以對于任意一個實數ε>0,總存在一個滿足式 (26)的實數r,使得由滿足不等式‖x0-xbest‖≤r的任一初態x0出發的運動都滿足不等式: 即方程的解x(t:x0,t0)始終都在圓S(r) 內。因此,圓S(r)的半徑r與t0無關,所以GLFWA-CM 算法的平衡狀態xbest是一致穩定的。又GLFWA-CM 算法必然可以收斂到全局最優: 所以此平衡狀態是漸近穩定的。此時,從S(r)內某點x0出發的軌跡不僅不會超出S(ε),且當t→∞時收斂于xe,即xbest。所以GLFWA-CM算法的平衡狀態xbest是一致漸進穩定的。綜上所述,GLFWA-CM 算法的平衡狀態xbest不僅是李雅普諾夫意義下穩定的,且平衡狀態是一致漸進穩定的。 圖3(a)~(d)展示的是30維情況下各算法獨立運行20次得到的四種測試函數的箱型圖(是一種用作顯示一組數據分散情況資料的統計圖,實線從上到下分別表示上邊緣、上四分位數、中值、下四分位數、下邊緣,空心圓圈表示異常值,叉號表示平均值)。為了便于觀察,將所有數據都進行min-max標準化處理,使其分布在[0,1]區間內。f1 函數是單峰函數,f3 函數是簡單多峰函數,f8函數是混合函數,f10函數是復合函數。在圖2(a)~(d)中,GLFWA-CM算法的數據最小,而且最集中,圖中五條實線基本成了一條直線。由于圖中數據是根據適應度值得到的,所以圖中數據越小,說明適應度值越小,算法的精度越高,圖中數據越集中,說明數據波動越小,算法的穩定性越好。 圖3 測試函數f 1、f 3、f 8、f 10 的箱型圖(D=30)Fig.3 Box plots of test functions f 1、f 3、f 8、f 10(D=30) 3.3.3 算法復雜度分析 煙花種群規模為N,變異火花數目M=N,問題維數為D,最大迭代次數為Gmax,總的爆炸火花數目為S,S一般大于N。由于大部分復雜問題計算適應度值所花的時間要遠大于一些簡單計算的時間,所以分析算法的時間復雜度主要是分析計算適應度值的耗時。假設平均每次計算適應度值的時間消耗為O(f),每次迭代都要計算所有火花的適應度值,共迭代了Gmax次,所以總的時間消耗O(F)=Gmax×S×O(f)。除計算適應度值外,算法還有一些額外的時間消耗,主要是一些簡單計算,下面是對這些額外開銷的分析。 FWA 的額外計算開銷主要產生在三個部分:一是爆炸算子,時間復雜度是O(Gmax×S×D);二是變異算子,時間復雜度是O(Gmax×N×D);三是選擇算子,由于要計算候選者集合中每個個體到其他個體之間的距離之和,所以時間復雜度是O(Gmax×S2×D)。由于N一般遠小于S,綜上所述,略去低階項,FWA 算法的額外時間復雜度為O(Gmax×S2×D)。 GLFWA-CM的額外計算開銷也是主要產生在這三個部分:一是爆炸算子,時間復雜度是O(Gmax×S×D);二是變異算子,由于要計算協方差矩陣,所以時間復雜度是O(Gmax×S×D2) ;三是選擇算子,時間復雜度是O(Gmax×S)。綜上所述,略去低階項,GLFWA-CM算法的額外時間復雜度為O(Gmax×S×D2)。 EFWA在選擇過程中采用了一種新的選擇策略,大大降低了計算量,選擇過程的時間復雜度為O(Gmax×S),爆炸算子與變異算子的時間復雜度與FWA 一樣,所以總的額外時間復雜度是O(Gmax×S×D)。 AFWA是在EFWA的基礎上,對核心煙花的爆炸幅度進行了自適應調整,雖然計算量稍微增多,但是還是和EFWA 在同一個量級,總的額外時間復雜度還是O(Gmax×S×D)。 dynFWA 是在EFWA 的基礎上對核心煙花的爆炸幅度進行了動態調整,同時,dynFWA 中還去除了變異算子這個步驟,所以變異算子的時間復雜度為O(0),所以總的額外時間復雜度是O(Gmax×S×D)。 CoFFWA是在dynFWA的基礎上加入了獨立選擇和避免擁擠策略,選擇過程的時間復雜度為O(Gmax×S),其他部分時間復雜度與dynFWA一樣,所以總的額外時間復雜度為O(Gmax×S×D)。 CoFFWA-CM 是在CoFFWA 的基礎上加入了協方差變異,協方差變異算子的時間復雜度和GLFWA-CM一樣,所以總的額外時間復雜度為O(Gmax×S×D2)。 LoTFWA用引導火花代替高斯變異火花,時間復雜度為O(Gmax×S×D),爆炸算子時間復雜度是O(Gmax×S×D),在選擇過程中采取了一種淘汰錦標賽策略,時間復雜度為O(Gmax×S),所以總的額外時間復雜度是O(Gmax×S×D)。 綜合分析可知,在比較的八種算法中,計算適應度值的時間消耗都是O(F)。對于一些簡單計算,FWA、CoFFWA-CM 和GLFWA-CM 的額外開銷相對其他五種算法稍大。FWA 主要是選擇過程計算開銷較大,CoFFWA-CM和GLFWA-CM主要是產生變異火花過程計算開銷較大。由于煙花算法的主要時間消耗還是O(F),這些簡單計算的開銷對算法時間復雜度的影響相對較小,所以在解決一些實際問題時,這些算法的實際耗時差距并不那么明顯。 總的來說,雖然GLFWA-CM 算法的時間復雜度比除FWA和CoFFWA-CM以外的其他算法稍大,但是,在求解精度和穩定性上,GLFWA-CM 要優于其他所有煙花算法。 本文針對傳統煙花算法中存在的尋優精度差,容易陷入局部最優等問題提出了一種基于錦標賽精英學習與協方差變異的煙花算法(GLFWA-CM)。該算法在爆炸算子中利用核心煙花更新信息確定核心煙花在每一維上的爆炸半徑以及其火花分布,加強了每一代核心煙花之間的聯系;在變異算子中用協方差變異代替了原來的高斯變異,使得變異火花分布在煙花附近的搜索區域,有效平衡了煙花算法的局部搜索和全局搜索能力;在煙花選擇過程中加入了基于錦標賽的精英學習策略,有效改善了煙花算法收斂速度慢的問題。本文對GLFWA-CM 算法的收斂性和穩定性進行了證明,并通過一系列的實驗表明,在低維和高維的情況下,GLFWACM算法均表現出不俗的性能,在算法的收斂性和穩定性上總體要強于其他比較算法。同時,分析得出GLFWACM 算法的時間復雜度比除FWA 和CoFFWA-CM 以外的其他算法稍大。綜上所述,證明了本文提出算法的正確性、有效性和適用性。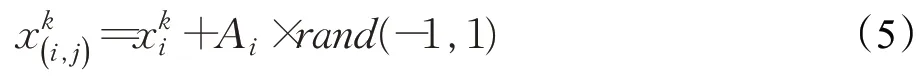

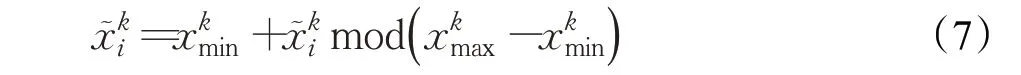
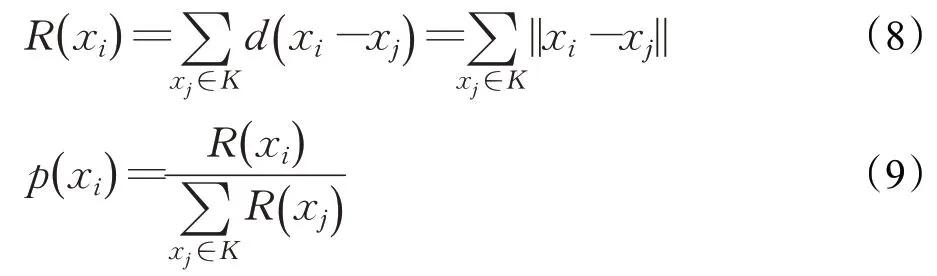
2 GLFWA-CM算法
2.1 爆炸算子



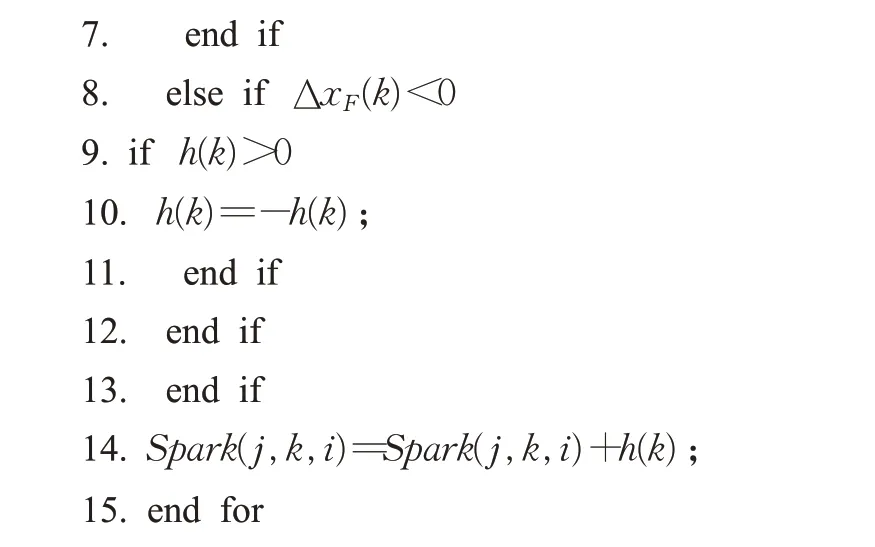
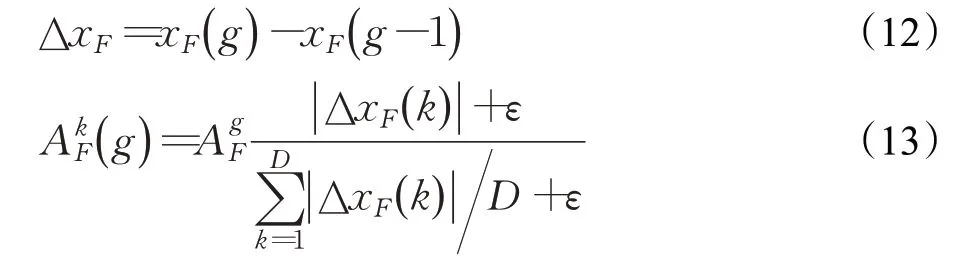
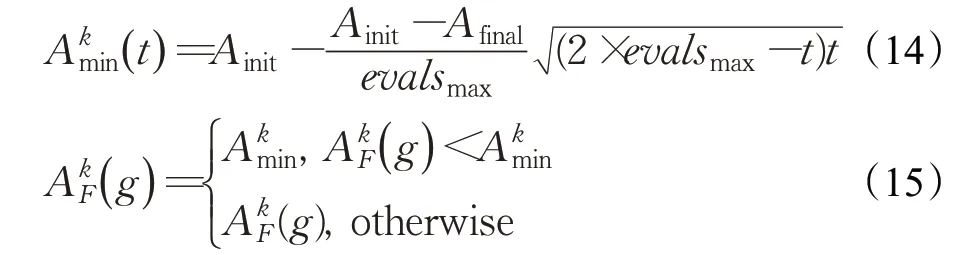
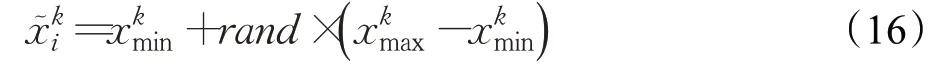
2.2 協方差變異算子

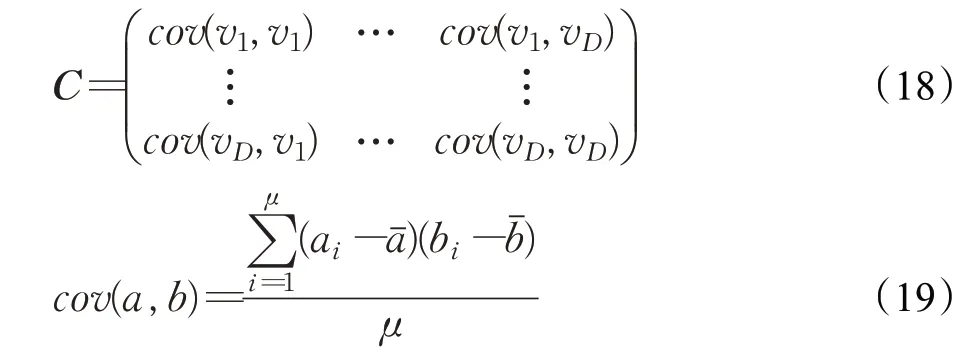
2.3 選擇策略
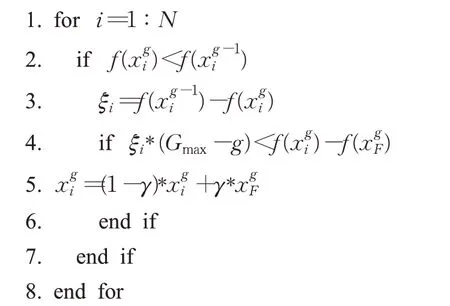
2.4 GLFWA-CM算法流程
3 實驗分析
3.1 參數設置
3.2 測試函數
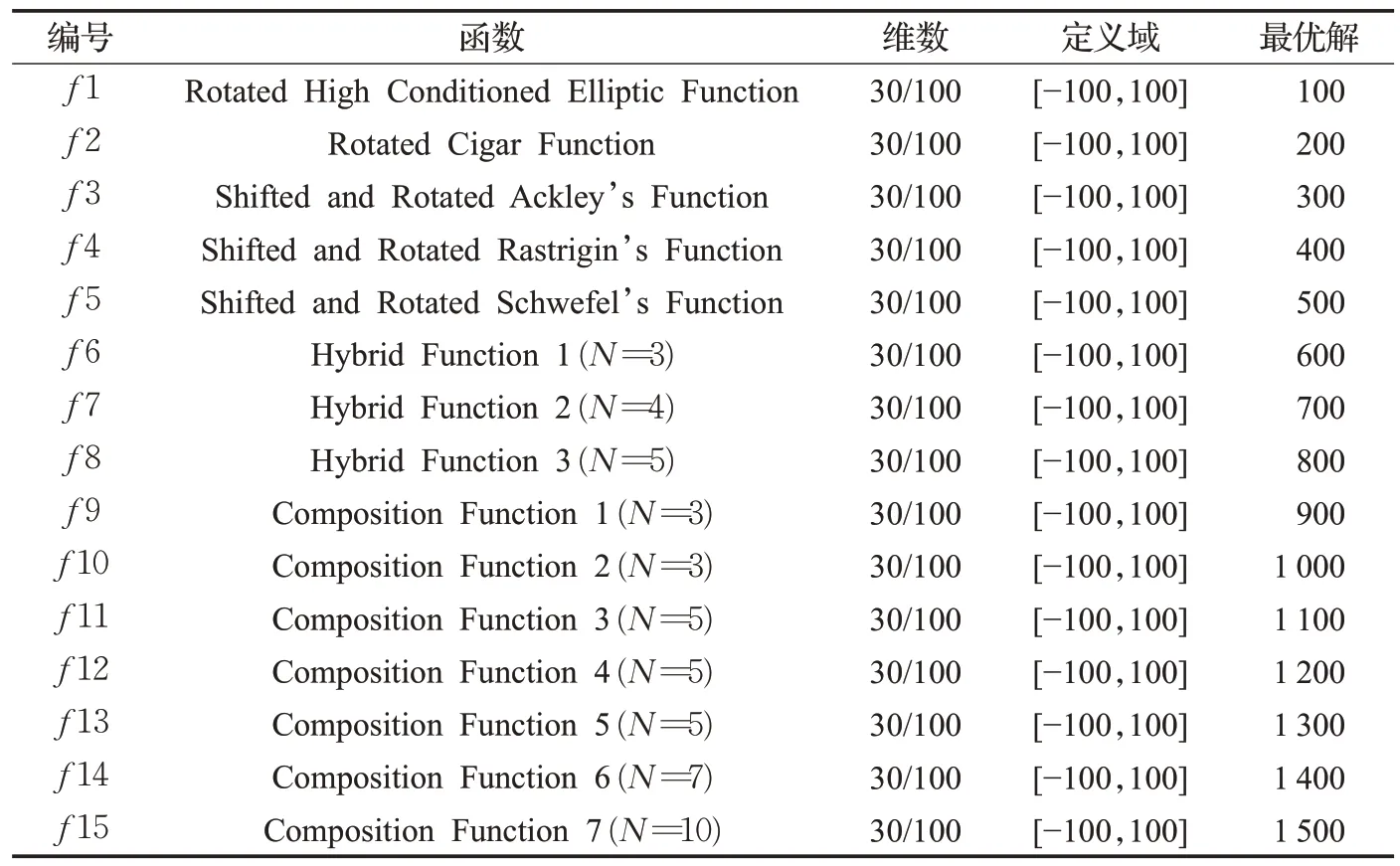
3.3 實驗結果與分析








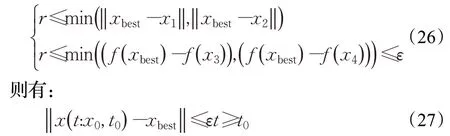
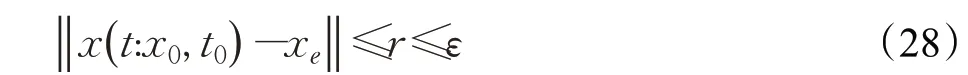
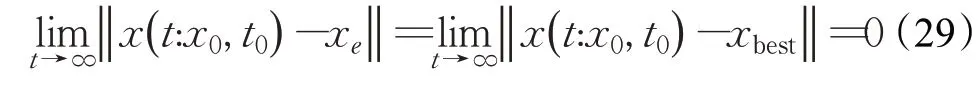
4 結語

