基于特征模型的疏浚泥漿濃度與流速聯合控制研究

麻天一，高 嵐，徐合力，朱漢華

(武漢理工大學 能源與動力工程學院，湖北 武漢 430063)

絞吸式挖泥船作為疏浚作業中最重要的設備，對改善河道環境和加強通航能力產生重要作用[1]。為了提高絞吸式挖泥船的疏浚作業產量和效率，有必要對疏浚作業進行自動化研究[2]。

在國內，只有較少單位在開展一些研究工作。唐建中、閉治躍等人[3]使用參數自校正前饋控制方法來實現泥漿濃度控制，并運用零極點配置自校正方法對流速進行控制；朱文亮、倪福生等人[4]提出了基于疏浚系統狀態空間模型的線性二次型最優控制策略來對泥漿濃度進行控制；高國章等人[5]提出了基于模糊PID 控制方法對泥漿濃度進行有效控制；潘成廣等人[6]利用無模型自適應前饋控制算法來控制泥漿流速；朱師倫等人[7]采用自適應控制算法對泥漿濃度進行有效控制。

泥漿濃度與流速控制存在耦合性與建模困難問題，很難從機理上建立其數學模型。因此從工程應用角度出發，借鑒吳宏鑫提出的“特征建模”理論，建立濃度與流速的雙輸入雙輸出的特征模型，并基于全系數自適應控制理論，設計全系數自適應控制器[8]。對于多輸入多輸出系統，特征建模在不同的領域取得了豐富的理論成果，并在一些實際工程中得到了應用[9-10]。這方面的研究可以同時對泥漿濃度與流速進行有效控制，以達到優化整個疏浚過程的目的，促進疏浚作業產量和效率。

1 泥漿濃度與流速特征建模

特征建模不需要通過機理建立模型，根據對象特征和控制要求，主要反應輸入和輸出的關系，并且特征模型輸出與實際輸出是等價的。對于高階復雜對象控制器的設計，特征建模方法具有很好的工程實用性[11]。

1.1 泥漿濃度與流速特征模型的建立

在實際疏浚過程中，由于不能短時間內多次改變臺車推進距離(縱向)和斗橋的位置(垂直方向)，所以主要控制橫移速度來控制泥漿濃度；挖泥船的泥泵電機控制泥泵，泥泵控制泥漿流速，因此可以通過調節泥泵轉速來控制泥漿流速。本文以橫移速度與泥泵轉速為輸入，泥漿濃度與泥漿流速為輸出，來建立雙輸入雙輸出特征模型。

根據高階系統特征建模原理，不考慮噪聲情況下，其控制量和輸出的關系可表示為：

X(n)(t)+An-1X(n-1)(t)+An-2X(n-2)(t)+…

+A2X(2)(t)+A1X(1)(t)+A0X(t)=

Bm(t)U(m)(t)+Bm-1(t)U(m-1)(t)+…+

B2(t)U(2)(t)+B1(t)U(1)(t)+B0(t)U(t),

(1)

式中,U(t)為控制量，X(t)為輸出，均為n維列向量；X(n)(t)表示對t時刻的輸出n次求導；An(t)(n=0,1,2,…)、Bm(t)(m=0,1,2,…;m≤n-1)為特征模型系數矩陣，均為n階矩陣。

經過形式變換、求導及離散化整理可得如下參數估計方程：

X(k+1)=F1(k)X(k)+F2(k)X(k-1)+G0(k)U(k)+G1(k)U(k-1),

(2)

式中，F1(k)、F2(k)、G0(k)和G1(k)為特征參數矩陣。

泥漿濃度與流速過程可根據公式(2)重構為特征模型形式：

(3)

式中特征參數矩陣可表示為：

式中，x1(k)表示k時刻泥漿濃度；x2(k)表示k時刻泥漿流速；u1(k)表示k時刻橫移速度；u2(k)表示k時刻泥泵轉速。

在不過分追求精度的前提下，同時也為方便后續控制器的設計，輸入僅取G0(k)一項，同時考慮到“全系數之和為單位矩陣I”的約束條件與時滯的影響，將公式(3)的特征模型形式優化改進如下：

(4)

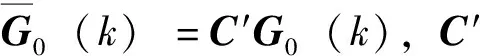
1.2 特征參數在線辨識

本文選擇最小二乘法與遞推算法相結合的方法，對泥漿濃度與流速的特征模型參數進行在線辨識，并采用遺忘因子λ進行控制。其中遺忘因子的作用是防止數據飽和，消除時變環境下之前的環境對本系統產生的影響，使辨識出來的參數可以最大限度地真實反應當前環境影響。

將公式(4)轉化成最小二乘的形式：

X(k+1)=ΨT(k)θ(k+1),

(5)

遞推最小二乘估計的公式如下：

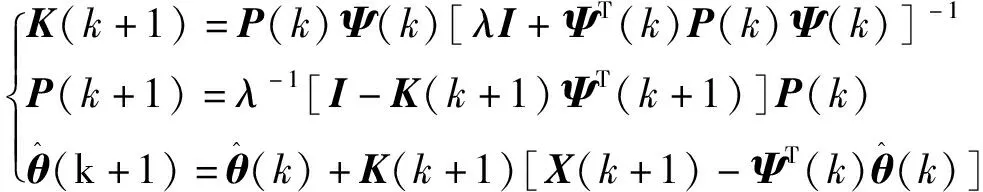
(6)

1.3 泥漿濃度與流速特征模型的驗證

1.3.1 泥漿濃度與流速數據預處理

在長江航道局的絞吸式挖泥船實際工作中進行數據采集，現截取一部分橫移速度、泥泵轉速、泥漿濃度和泥漿流速數據，采樣周期0.5 s，采樣時間為上午10時36分0秒至10時44分20秒，實測橫移速度變化曲線見圖1，實測泥泵轉速變化曲線見圖2，實測泥漿濃度變化曲線見圖3，實測泥漿流速變化曲線見圖4。

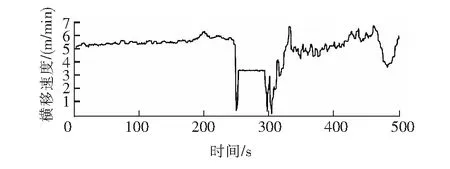
圖1 實測橫移速度變化曲線

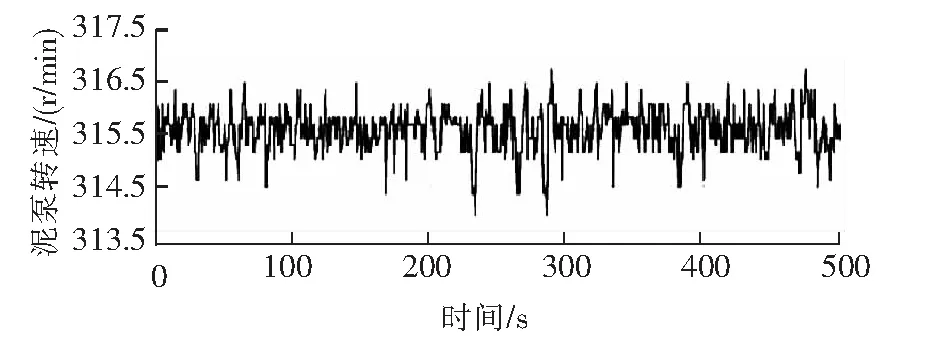
圖2 實測泥泵轉速變化曲線

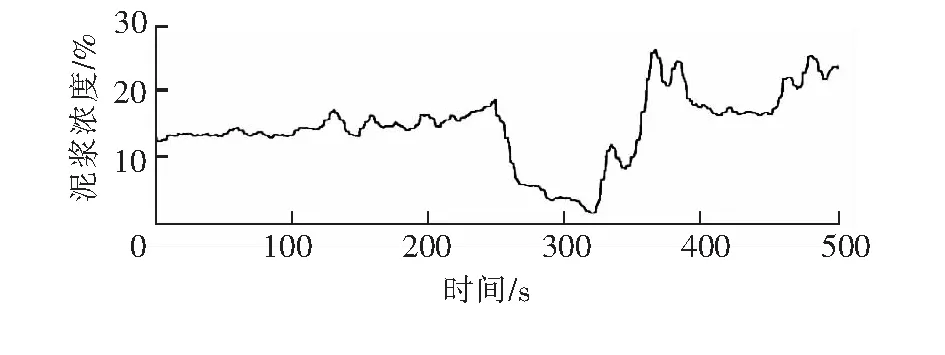
圖3 實測泥漿濃度變化曲線

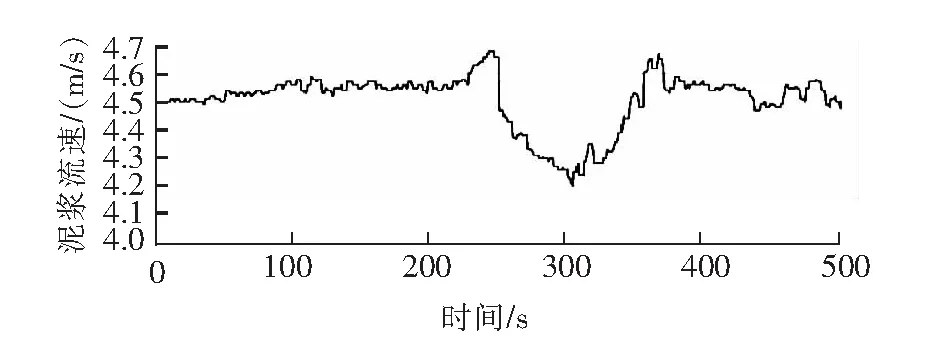
圖4 實測泥漿流速變化曲線

以上數據中存在一些野點，對泥漿濃度與流速的特性造成影響，同時為了把數據轉換成易處理的形式，方便后續工作的順利進行，需對數據進行剔除野點、濾波等處理。預處理后橫移速度變化曲線見圖5，泥泵轉速變化曲線見圖6，泥漿濃度變化曲線見圖7，泥漿流速變化曲線見圖8。

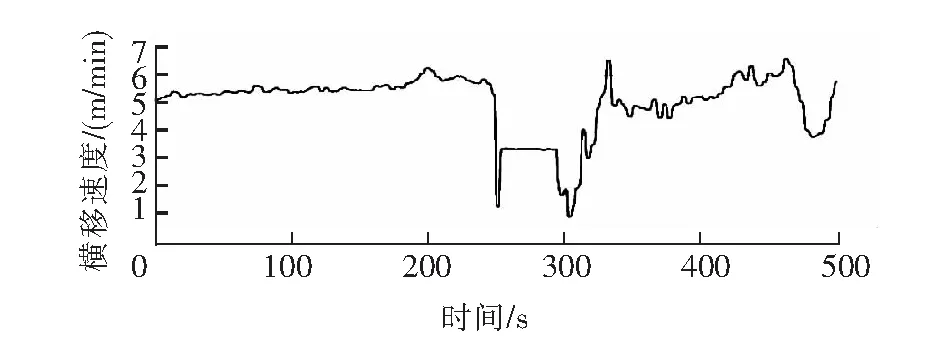
圖5 預處理后橫移速度變化曲線

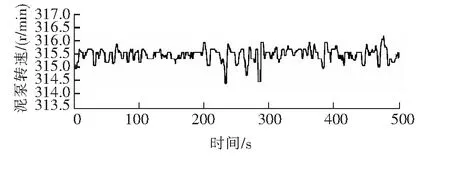
圖6 預處理后泥泵轉速變化曲線

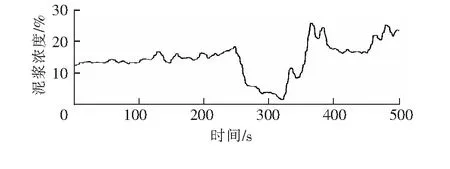
圖7 預處理后泥漿濃度變化曲線

圖8 預處理后泥漿流速變化曲線

由圖6～圖8可以看出，以上實測數據經過剔除野點和濾波等處理后，變化曲線變得平滑了一些(數據預處理不能讓曲線變得過分平滑，否則會失去數據的真實特性)，有利于后續特征模型驗證與控制器設計等工作的開展。

將預處理后的數據經過計算機離線辨識，確定時滯時間為10 s，滯后步數τ=20。

1.3.2 泥漿濃度與流速特征模型的驗證

為驗證該雙輸入雙輸出特征模型的準確性，將實測的泥漿濃度與流速數據與特征模型的輸出作對比，泥漿濃度對比圖見圖9，泥漿流速對比圖見圖10。根據圖9、圖10可以看出，特征模型的輸出曲線和實測的泥漿濃度與流速曲線吻合程度較高，在疏浚動態過程中泥漿濃度與流速能保持在允許的輸出誤差范圍內。因此從控制角度來看，在同樣的輸入環境下，該特征模型能較好地模擬實際的泥漿濃度與流速過程，具有較好的工程實用性。

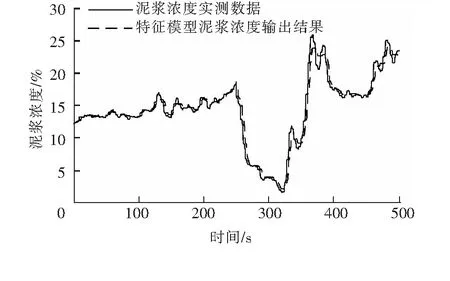
圖9 泥漿濃度對比圖

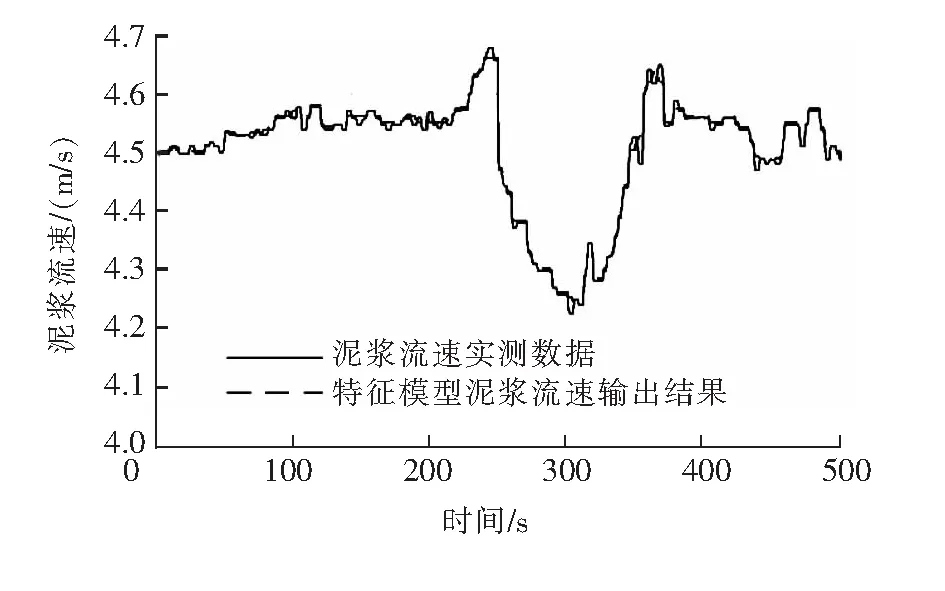
圖10 泥漿流速對比圖

2 泥漿濃度與流速控制器設計

絞吸挖泥船泥漿濃度與流速的控制系統是具有耦合性的復雜系統，對其進行聯合控制器的設計，泥漿濃度與流速的聯合控制器設計示意圖如圖11所示。

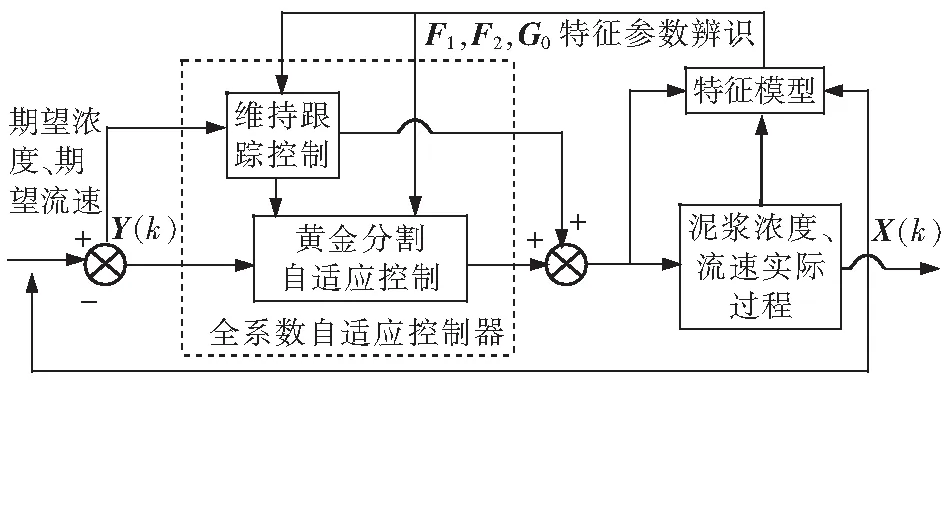
圖11 泥漿濃度與流速的聯合控制器設計示意圖

在圖11中，X(k)為實際泥漿濃度與流速的輸出；Y(k)為期望泥漿濃度與流速輸出和實際輸出的誤差。根據疏浚泥漿濃度與流速的控制需求，本文采用黃金分割自適應控制和維持跟蹤控制相結合的控制策略。

2.1 黃金分割自適應控制器的設計

黃金分割自適應控制，是把黃金分割比(l1/l2=0.382/0.618)與最小方差控制思想相結合的一種新型控制器設計方法。根據構建的特征模型，設計的黃金分割自適應控制律為：

(7)

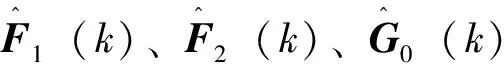
2.2 維持/跟蹤控制器的設計

黃金分割自適應控制雖然能提高控制系統的穩定性，但疏浚系統復雜，僅依靠此控制方法不能完全滿足泥漿濃度與泥漿流速的控制需求。因此，本文采用黃金分割自適應控制和維持/跟蹤控制相結合的控制方式，根據泥漿濃度與流速過程的特征模型，設計的維持/跟蹤控制律如下：

(8)

式中，uw(k)為維持跟蹤控制律的輸出。

為避免控制律輸出不穩定，本文采用濾波原理對其進行處理，使輸出保持在一個相對平穩的狀態，濾波后的輸出為：

uw′(k)=(1-η)uw′(k-1)+ηuw(k),

(9)

式中，uw′(k)為濾波優化后維持/跟蹤控制律的輸出；η為濾波系數，本文取η=0.3。

3 泥漿濃度與流速控制系統的仿真研究

根據實際疏浚情況，泥漿濃度與流速維持穩定是最理想的工作狀態，是疏浚作業過程中很重要的部分，因此對泥漿濃度與流速進行恒值控制仿真實驗驗證。通過綜合考慮及計算，本文設定期望泥漿濃度為20%、期望泥漿流速為4.5 m/s，進行仿真實驗驗證，采樣周期同樣為0.5 s。

3.1 單輸入單輸出恒值控制仿真實驗驗證

對于單輸入單輸出全系數自適應控制器，當單獨控制泥漿濃度時，將泥漿流速作為一個可變干擾，由于濃度與流速耦合關系的影響，泥漿濃度變化會使流速發生改變。同樣采用特征建模方法，將式(4)模型變為單輸入單輸出，輸入為橫移速度，輸出為泥漿濃度，使用黃金分割控制加維持/跟蹤控制的方法進行控制，得到單輸入單輸出全系數自適應控制器的恒值控制仿真結果，目的是使濃度在整個過程中維持在本文規定的期望濃度(20%)附近，單輸入單輸出全系數自適應控制濃度變化曲線和流速變化曲線如圖12、圖13所示。

圖12 單輸入單輸出全系數自適應控制濃度變化曲線

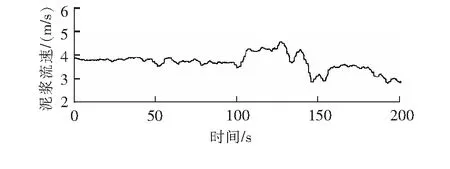
圖13 單輸入單輸出全系數自適應控制流速變化曲線

由圖12、圖13可以看出，單獨控制泥漿濃度時，雖然能較好地將濃度穩定在期望值附近，但由于耦合作用的影響，流速在整個過程中一直變化，很不穩定。流速的變化會影響期望產量，不利于達到控制目的。

3.2 雙輸入雙輸出恒值控制仿真實驗驗證

對于本文設計的雙輸入雙輸出全系數自適應控制器，輸入為橫移速度與泥泵轉速，輸出為泥漿濃度與泥漿流速，得到其恒值控制仿真結果，雙輸入雙輸出全系數自適應控制濃度變化曲線和流速變化曲線如圖14、圖15所示。由圖14、圖15的仿真結果可看出，設計的雙輸入雙輸出全系數自適應控制器能較好地將泥漿濃度與流速均穩定在期望值附近，經計算泥漿濃度與流速的誤差率能保持在5%以內，具有很好的適應性。

圖14 雙輸入雙輸出全系數自適應控制濃度變化曲線

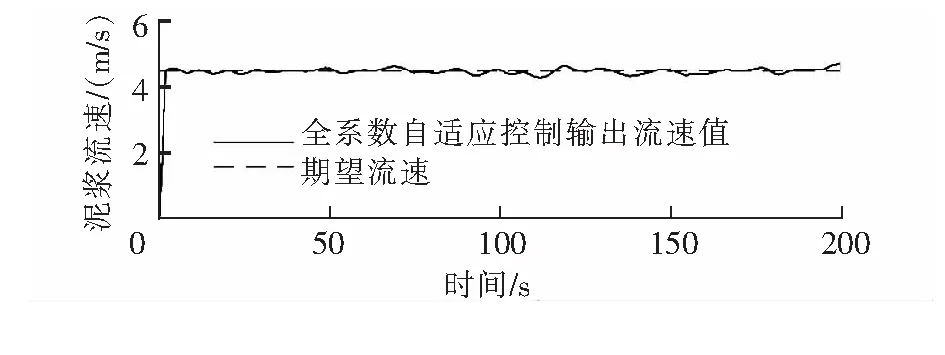
圖15 雙輸入雙輸出全系數自適應控制流速變化曲線

4 結束語

本文針對泥漿濃度與流速過程控制中的建模困難和耦合性的問題，構建了雙輸入雙輸出特征模型，并設計自適應控制器，達到了對泥漿濃度與流速雙控的效果。通過恒值仿真實驗驗證，本文設計的基于雙輸入雙輸出特征模型的全系數自適應控制器能使泥漿濃度與流速保持在期望值，并且有很好的跟蹤性能。