山重水復疑無路,柳暗花明又一村
李子奇

中圖分類號:A 文獻標識碼:A 文章編號:(2021)-33-426
在初中數學中,一些概念往往看似簡單,但學生不能正確地理解概念,更不能靈活地應用所學概念解決問題,其原因主要是因為學生的天性傾向于依賴直觀和具體。特別當情景或圖形發生變化時,他們不知所措,無法用所學知識進行分析問題,解決問題。因此,數學概念的教學,教師要挖掘教材,引導學生從表面到本質理解概念的內涵與外延,把握概念的深層結構,要善于掌握更多的典型、精彩的例子,深刻探究概念的“七十二般變化”,只有這樣,才能引領學生充分地理解概念的核心部分,掌握一定的分析方法,數學學習才能高效。
本文通過“對同位角、內錯角、同旁內角”的概念教學,說明如何挖掘概念的核心部分,突破教學難點。
人民教育出版社《數學》七年級下冊,第五章 相交線與平行線中,第三節內容為“同位角、內錯角、同旁內角”。教材通過具體圖形給出了“同位角、內錯角、同旁內角”的概念,看似簡單、具體、明了。實際上,經過幾年的教學經驗發現絕大多數同學不能正確地理解這三個概念,所做的習題一塌糊涂,只是想當然的進行判斷。
在教學探究中不難發現,無論是同位角、內錯角、還是同旁內角的兩個角,它們的共性是,兩角的四條邊中,有兩條邊所在的直線是同一條直線,實質上這條直線就是第三條直線,其余兩條邊所在的直線就是第一、二條直線。因此,教學過程中指導學生尋找出兩個角的四條邊,根據特定圖形觀察找出兩個角的公共邊,即第三條直線,就能順利而正確地判斷哪兩條直線被第三條直線所截,再根據兩個角在第三條直線的兩側或同側,與第一、二條直線的位置關系,就能輕而易舉地得出兩個角的位置關系。
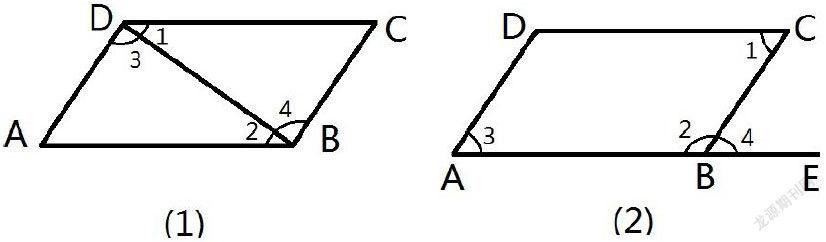
例1、 如圖,∠1和∠2,∠3和∠4各是哪兩條直線被哪一條直線所截形成的?它們各是什么角?(人民教育出版社七年級《數學》下冊,第9頁第11題)
分析:在圖(1)中,∠1是由DB和DC兩條直線組成的角;∠2是由DB和AB兩條直線組成的角;在四條直線中,DB重合則是第三條直線,即∠1和∠2是DC和AB兩條直線被DB所截;又因為∠1和∠2分布于DB兩側,在AB和DC之間,所以是內錯角。
在圖(2)中,∠1是由DC和CB組成,∠2是由AB和BC組成,重合的直線是BC,即BC是第三條直線,而∠1和∠2分布于BC的同側,在DC和AB之間,因此,它們是DC和AB被直線BC所截得到的同旁內角。
在圖(2)中,∠3是由AD和AB組成,∠4是由BC和BE組成,而AB和BE是同一條直線,即它們是AD和BC被AE所截得到的同位角。
能正確判斷對同位角、內錯角、同旁內角,就很容易掌握平行線的性質及判定。
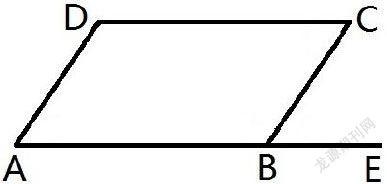
例2、如圖,BE是AB的延長線,(1)由∠CBE=∠A可以判定哪兩條直線平行?根據是什么?(人民教育出版社七年級《數學》下冊,第15頁,練習第1題)
分析:由角的關系要判斷直線的位置關系,實質上也是判定哪兩條直線被哪一條直線所截,第一、二條直線就有可能是平行線。
因為∠CBE是由BC和BE組成,∠A是由AD和AB組成,而AB和BE是同一條直線,即是第三條直線,故說明BC和AD被AE所截,又因為∠CBE=∠A是同位角且相等,所以AD∥BC
以上,同位角、內錯角、同旁內角的判斷相比較容易,關鍵是圖形背景和教材上所學概念時的圖形很相近,用這種方法去判斷顯得比較麻煩,可是當圖形背景變化時,方能顯出這種方法的優越性和用武之地。
例3、如圖,∠1與哪個角是內錯角,與哪個角是同旁內角?∠2與哪個角是內錯角,與哪個角是同旁內角?它們分別是哪兩條直線被哪一條直線所截形成的?(人民教育出版社七年級《數學》下冊,第7頁,練習第2題)
分析:∠1是由AB和BC組成,當AB為公共邊時,即AB是第三條直線,從圖中可以看出AB既是∠DAB的一條邊,又是∠BAE的一條邊,因此,DA和BC被AB所截∠1和∠DAB是內錯角,∠1和∠BAE是同旁內角;當BC為公共邊時,則BC又是∠BCA的一條邊,因此,AB和AC被BC所截,且∠1和∠2是同旁內角;
同理,可以分析∠2的內錯角與同旁內角。
順便一提,我覺得這道題不適宜作為練習題,應該安排在習題的拓展探索部分中,因為,這道題顯然并不簡單。
課堂教學中概念和方法是學習過程中一個重點,是走向知識深處的一支撐點,而數學概念的教學理解又是一個永無止境的過程,因此,希望我們廣大數學教師在數學概念的教學理解上下一番苦功,掌握從大量知識中汲取促進數學教學營養的能力,從而使自己進入數學教學的自由王國。

