反向Ⅱ型fold-fold的正則化系統(tǒng)的動力學分析

方之昊, 陳興武

(四川大學數(shù)學學院， 成都 610064 )

1 引 言

平面逐段光滑系統(tǒng)被廣泛地應用于建筑、機械、電網等領域[1-5]，它的研究是微分動力系統(tǒng)研究熱點之一.本文利用S-T正則化方法來構造反向II型fold-fold逐段光滑系統(tǒng)的正則系統(tǒng). 這類逐段光滑系統(tǒng)有一個焦點, 且在一定條件下會在參數(shù)擾動時產生一個極限環(huán), 類似于解析系統(tǒng)中的Hopf分岔. 本文給出了正則系統(tǒng)在雙參數(shù)擾動下的局部動力學行為, 指出正則系統(tǒng)的平衡點要么為結點, 要么為焦點，且焦點的穩(wěn)定性和階數(shù)會隨著參數(shù)變化而變化.這就導致Hopf分岔的發(fā)生.

考慮一個有如下形式的平面系統(tǒng)

(1)

X±(x,y)=(P±(x,y),Q±(x,y))T

為定義在R2上的光滑向量場. 我們稱系統(tǒng)(1)為一個逐段光滑系統(tǒng),y=0為切換流形Σ，并且系統(tǒng)

(2)

為上子系統(tǒng), 系統(tǒng)

(3)

為下子系統(tǒng).

Filippov[6]針對此類系統(tǒng)做出了大量的研究和總結, 其成果被后人稱為Filippov約定.對于切換流形Σ上任意一點p:(x,0), 定義

(4)

如果H(x)=0, 則p要么是某子系統(tǒng)的平衡點, 要么是某個子系統(tǒng)的切點. 若是前者, 我們稱p是逐段光滑系統(tǒng)(2)的邊界平衡點; 若是后者, 我們稱p為逐段光滑系統(tǒng)(1)的切點. 不失一般性,p固定為原點(0,0). 假設(0,0)是一個切點.若

則稱切點(0,0)是逐段光滑系統(tǒng)(1)的一個fold-fold. 若進一步有

P+(0,0)>0,P-(0,0)<0,

則稱切點(0,0)是逐段光滑系統(tǒng)(1)的一個反向II(Invisible-Invisible) 型fold-fold. 如圖1所示.

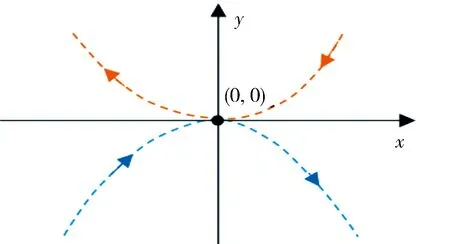
圖1 藍色(橘色)虛線表示上(下)子系統(tǒng)軌道(線上彩色)Fig.1 The blue (orange) dot curve denotes the orbit of upper(lower) subsystem(color online)

在本文中, 我們假設(0,0)是逐段光滑系統(tǒng)(1)的反向II型fold-fold. 由文獻[7]提出的正則化理論, 逐段光滑系統(tǒng)(1)有如下形式的正則系統(tǒng)

(5)

其中0<ε?1,

文獻[8]發(fā)現(xiàn)了正則系統(tǒng)的快慢結構, 文獻[9]發(fā)現(xiàn)了快慢系統(tǒng)的臨界流形和慢子系統(tǒng)向量場分別與滑行區(qū)域和滑行向量場是微分同胚的. 隨后，文獻[10]研究了Saddle-fold類型的正則系統(tǒng)并給出分岔圖.文獻[11]在某非退化條件下給出了反向II型fold-fold正則系統(tǒng)的焦點量對正則函數(shù)φ(s)的依賴關系并進一步給出Hopf 分岔曲線.文獻[12]研究了反向II型fold-fold為0.5階細焦點時正則系統(tǒng)的動力學.本文根據(jù)散度(div(P+,Q+)+div(P-,Q-))|(0,0)的不同情況研究具有反向II型fold-fold的逐段光滑系統(tǒng)(1)所對應的正則系統(tǒng)(5)及其擾動系統(tǒng)的動力學行為.

我們在第2節(jié)中給出了一些預備知識及本文的主要結果，并在第3節(jié)中給出其證明. 在第4節(jié)中, 我們結合例子對主要結果給出一些重要注釋.

2 預備知識與主要結果

對于任意一點p:(x,y)∈R2, 如文獻[6]定義集合

可知, 當p∈Σ時,F(p)是一個閉凸集. 由文獻[6], 一個絕對連續(xù)函數(shù)ψ(t)若幾乎處處滿足微分包含式ψ′(t)∈F(ψ(t))則稱為逐段光滑系統(tǒng)(1)的解. 從而逐段光滑系統(tǒng)(1)有一個解ψ(t)=(0,0). 然而，對任意初值點(x0,0),x0>0, 其正向軌道先位于下半平面并且與Σ相交于(x1,0),x1<0, 隨后進入上半平面, 與Σ相交于(x2,0),x2>0.為了更精確地描述這一現(xiàn)象并且方便計算，我們根據(jù)文獻[6,13]定義龐加萊返回映射P(x)的等價形式. 當x1∈(-∞,0)時, 定義兩個函數(shù)

并且當x0,2∈[0,+∞)時定義

那么在Σ上, 等價形式被定義為

進一步，由文獻[6]可知, 當P±(x,y),Q±(x,y)∈Ck(k=1,2,…∞,ω)時有P(x)∈Ck. 不妨假設P±(x,y),Q±(x,y)∈Cω.那么可以將P(x)寫為

我們采用文獻[13]中關于細焦點的階的定義, 即如果有V1=V2=…=Vk=0但Vk+1>0(<0), 則稱點(0,0)為逐段光滑系統(tǒng)(1)的一個k/2階不穩(wěn)定(穩(wěn)定)細焦點. 在此定義下, 雖然逐段光滑系統(tǒng)(1)的焦點(0,0)的階數(shù)可能為分數(shù), 但它統(tǒng)一了解析系統(tǒng)和逐段光滑系統(tǒng)對焦點階數(shù)的定義.

除焦點外, 也可能存在一點(x0,0)∈Σs使得Xs(x0,0)=0, 那么我們將該點稱為一個偽平衡點.此時，存在一個解

ψ(t;(x0,0))=(x0,0).

進一步, 如果當x≠x0時(x-x0)Xs(x,0)的第一個分量小于0，且

Q+(x0,0)<0,Q-(x0,0)>0,

則稱(x0,0)是一個穩(wěn)定的偽結點. 如果當x≠x0時(x-x0)Xs(x,0)的第一個分量大于0，且

Q+(x0,0)>0,Q-(x0,0)<0,

則稱(x0,0)是一個不穩(wěn)定的偽結點.此時我們考慮逐段光滑系統(tǒng)(1)的一個擾動, 即令Q-(x,y)=Q-(x-δ,y).那么，當δ>0且足夠小時, 由文獻[6,14]可知, 逐段光滑系統(tǒng)(1)的(0,0)會分散為上子系統(tǒng)(2)的切點(0,0)和下子系統(tǒng)(3)的切點(δ,0)，會產生滑行區(qū)域

Σs={(x,0)|x∈(0,δ)}

和滑行向量場. 若滑行向量場有一個偽結點, 并且偽結點和未擾動逐段光滑系統(tǒng)(1)的焦點具有不同穩(wěn)定性, 穿越極限環(huán)就會產生. 當δ<0且足夠小時, 情況是類似的. 這類現(xiàn)象被稱為偽Hopf分岔或逐段光滑系統(tǒng)的Hopf分岔.

在時間尺度變換及此類擾動下, 正則系統(tǒng)為

由于正則系統(tǒng)與逐段光滑系統(tǒng)在|y|≥ε的區(qū)域具有相同的軌道結構, 我們對正則系統(tǒng)的研究主要考慮帶狀區(qū)域R. 對未擾正則系統(tǒng)(6)δ=0, 即正則系統(tǒng)(5), 我們的得到如下結果.

定理2.1當

(div(P+,Q+)+div(P-,Q-))|(0,0)≠0

時存在ε0>0,使得對任意ε∈(0,ε0)正則系統(tǒng)(6)δ=0在(0,0)處具有一個粗焦點. 進一步, 當

(div(P+,Q+)+div(P-,Q-))|(0,0)>0(<0)

時此粗焦點不穩(wěn)定(穩(wěn)定).

對擾動正則系統(tǒng)(6), 我們有

定理2.2如果(div(P+,Q+)+div(P-,Q-))|(0,0)>0, 則當δ≠0足夠小時擾動正則系統(tǒng)(6)在(0,0)的小鄰域內有唯一平衡點且如圖 2a所示.

(i) 當δ>0時, 存在(δ,ε)空間中兩條曲線ε1(δ)和ε2(δ)滿足ε2(δ)>ε1(δ)以及：當ε<ε1(δ)時此平衡點為一個穩(wěn)定的正常結點；當ε=ε1(δ)時此平衡點為一個穩(wěn)定的退化結點；當ε1(δ)<ε<ε2(δ)時此平衡點為一個穩(wěn)定的粗焦點；當ε=ε2(δ)時此平衡點為一個階數(shù)不小于1的細焦點；當ε>ε2(δ)時此平衡點為一個不穩(wěn)定的粗焦點.

(ii) 當δ<0時, 存在(δ,ε)空間中一條曲線ε3(δ)滿足：當ε>ε3(δ)時此平衡點為一個不穩(wěn)定的粗焦點；當ε=ε3(δ)時此平衡點為一個不穩(wěn)定的退化結點；當ε<ε3(δ)時此平衡點為一個不穩(wěn)定的正常結點.

定理2.3如果(div(P+,Q+)+div(P-,Q-))|(0,0)<0, 則當δ≠0足夠小時擾動正則系統(tǒng)(6)在(0,0)的小鄰域內有唯一平衡點且如圖2b所示.

圖2 原點附近的參數(shù)空間(δ,ε)

(i) 當δ<0時, 存在(δ,ε)空間中兩條曲線ε4(δ)和ε5(δ)滿足ε5(δ)>ε4(δ)以及：當ε<ε4(δ)時, 此平衡點為一個不穩(wěn)定的正常結點；當ε=ε4(δ)時此平衡點為一個不穩(wěn)定的退化結點；當ε4(δ)<ε<ε5(δ)時此平衡點是一個不穩(wěn)定的粗焦點；當ε=ε5(δ)時此平衡點為一個階數(shù)不小于1的細焦點；當ε>ε5(δ) 時此平衡點為一個穩(wěn)定的粗焦點.

(ii) 當δ>0時, 存在(δ,ε)空間中存在一條曲線ε6(δ)滿足：當ε>ε6(δ)時此平衡點為一個穩(wěn)定的粗焦點；當ε=ε6(δ)時此平衡點為一個穩(wěn)定的退化結點；當ε<ε6(δ)時此平衡點為一個穩(wěn)定的正常結點.

由于函數(shù)φ(s)有無數(shù)種選取方式，且正則系統(tǒng)的動力學緊密依賴于它, 我們在定理2.2和定理2.3中給出了細焦點階數(shù)的下界，但不能確定細焦點的具體階數(shù). 我們將會在后面的例子中展示對不同的函數(shù)φ(s), 細焦點的階數(shù)是可以超過這兩個定理給出的下界.

3 主要結果的證明

定理2.1的證明 不失一般性, 我們對上子系統(tǒng)作時間尺度變換

dτ=-P+(0,0)dt/P-(0,0).

此時有

從而

這樣的變換不改變穿越區(qū)域、滑行區(qū)域以及偽平衡點的類型和穩(wěn)定性. 因此, 我們對逐段光滑系統(tǒng)(1)不妨假設

P+(0,0)=-P-(0,0)>0.

不難計算出(0,0)為正則系統(tǒng)(6)δ=0的平衡點. 那么對應的雅可比矩陣為

其特征多項式為

λ2-b1λ+b2-b3=0， 這里

因此, 我們得到特征值:

所以，若

則平衡點是不穩(wěn)定的粗焦點(穩(wěn)定).定理得證.

定理2.1表明，在散度條件約束下, 正則系統(tǒng)(6)是局部結構穩(wěn)定的.然而，逐段光滑系統(tǒng)(1)卻是結構不穩(wěn)定的, 并且前文已經說明它可能會發(fā)生偽Hopf分岔. 此時，一個很自然的問題是擾動正則系統(tǒng)(6)會不會發(fā)生Hopf分岔?定理2.2和定理2.3回答了此問題, 我們在下面給出它們的證明.

定理2.2的證明 定義函數(shù)

由定理2.1, 當δ=0且ε足夠小時, 在(x,y,δ)=(0,0,0)處有初值條件

κ1(0,0,0)=0,κ2(0,0,0)=0

和行列式

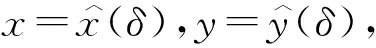
其中

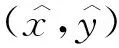
其中

將ai(δ,ε)關于δ在δ=0處進行泰勒展開，得到

a1(δ,ε)=a11(ε)+a12(ε)δ+O(δ2),

a3(δ,ε)=a31(ε)+a32(ε)δ+O(δ2),

進而，再將系數(shù)aij(ε)關于ε在ε=0處進行泰勒展開得到

a1(δ,ε)=(a111+O(ε))+(a121+O(ε))δ+

O(δ2),

O(δ2)},

a3(δ,ε)=(a311+O(ε))+(a321+O(ε))δ+

O(δ2),

(a421+O(ε))δ+O(δ2)},

其中

從而在δ與ε足夠小時我們得到a2(δ,ε)>0,a3(δ,ε)<0，其特征多項式為

λ2-(a1(δ,ε)+a4(δ,ε))λ+a1(δ,ε)a4(δ,ε)-

a2(δ,ε)a3(δ,ε)=0.

定義函數(shù)

4a1(δ,ε)a4(δ,ε)+4a2(δ,ε)a3(δ,ε).

將前面的展開式代入后可得

由于

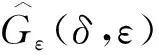
那么

(a111+a411)ε+a421δ+O(ε2,δ2,εδ).

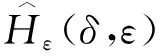
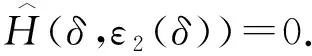
下證ε2(δ)>ε1(δ), 即對任意的滿足H(δ,ε)≥0的(δ,ε)有G(δ,ε)<0. 我們采用反證法.假設ε2(δ)≤ε1(δ).根據(jù)定理2.1可知, 可以選取某一(δ,ε)，使得H(δ,ε)>0而G(δ,ε)<0.此時，保持δ>0不變而令ε變小, 那么根據(jù)前文的討論和假設可知, 必然存在點(δ,ε)使得

H(δ,ε)=G(δ,ε)=0

或

H(δ,ε)>0且G(δ,ε)>0.

前一種情況對應ε2(δ)=ε1(δ)而后一種情況對應ε2(δ)<ε1(δ).下面我們分別討論.

對于前一種情況, 函數(shù)

G(δ,ε)=-4(a1(δ,ε)a4(δ,ε)-

a2(δ,ε)a3(δ,ε))=0.

但是，將前文中的ai,i=1,2,3,4的展開式代入后可得

這與假設是矛盾的.

對于后一種情況, 我們可以取(δ,ε)足夠靠近(δ,ε2(δ))并且G(δ,ε)>0, 使得H(δ,ε)>0且足夠小.此時

O(δ,ε))<0.

這與假設矛盾. 命題得證.

G(δ,ε)>0，H(δ,ε)<0.

G(δ,ε)=0，H(δ,ε)<0.

因此特征值為一對相同的負實數(shù).又因為

經過初等行變換后變?yōu)?/p>

當ε>ε1(δ)且ε<ε2(δ)時, 有

G(δ,ε)<0，H(δ,ε)<0.

G(δ,ε)<0，H(δ,ε)=0.

G(δ,ε)<0，H(δ,ε)>0.

當δ<0時, 曲線ε3(δ)的存在性和平衡點類型以及退化程度的證明是類似的. 這里我們省略其證明.證畢.

定理2.2表明,在散度條件下，在參數(shù)空間中確定了平衡點類型變化的臨界曲線和焦點階數(shù)變高的曲線. 通過對比，我們發(fā)現(xiàn), 逐段光滑系統(tǒng)(1)在δ的擾動下偽平衡點的類型直接從焦點轉化為結點.其主要原因是δ只會影響下子系統(tǒng).因而我們可以認為這是參數(shù)對逐段光滑系統(tǒng)(1)的部分擾動. 然而，在正則系統(tǒng)(6)中,δ的變化是對整個系統(tǒng)產生影響的, 且ε也會帶來影響.

定理2.3的證明 與定理2.2中類似, 在δ與ε足夠小時, 可以通過隱函數(shù)定理得到正則系統(tǒng)(6)的平衡點

+O(ε2))δ+O(δ2)),

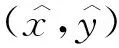
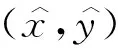
4 例

考慮如下平面逐段光滑系統(tǒng)：

直接計算可得

(div(P+,Q+)+div(P-,Q-))|(0,0)=1.

通過時間尺度變換t→2t, 其正則系統(tǒng)可寫為

特征值為

因此，(0,0)是一個不穩(wěn)定的粗焦點. 這與定理2.1的結果相吻合. 當δ>0時, 平衡點位于

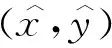
從而可得特征多項式

以及相應的特征值

定義函數(shù)

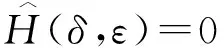
ε2(δ)=φ′δ+O(δ2).

另一方面,定義函數(shù)

同理，當δ<0足夠小時, 得

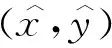
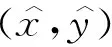
其特征值為

為計算其焦點量g3, 先假設正則函數(shù)φ(s)在s=0附近形式為

φ(s)=φ1s+φ3s3+h.o.t.,

其中φj表示sj的系數(shù). 由文獻[15]，計算可得

其中

C4(δ)+C5(δ),

根據(jù)正則函數(shù)φ的假設又有