平面五桿機構的諧波-多目標遺傳優化方法

王洪濤，李占賢

(1.華北理工大學 機械工程學院，河北 唐山 063210；2.河北省工業機器人產業研究院，河北 唐山 063010)

引言

平面并聯五桿機構[1]是一種結構簡單，并可適用于復雜惡劣應用環境的并聯機構。它具有剛度大，可實現復雜運動軌跡、承載能力強等特點，在并聯和混聯機器人機構中得到廣泛應用。

在平面并聯機構設計中，尤其是平面五桿機構的設計，目前以基于工作空間的圖解法為主,解析法的應用相對較少。在工程應用越來越多的高速運動環境中，對機構的動力響應特性及機構慣量等要求越來越高，使得圖解法求解精度較低，不能同時滿足多目標參數設計的缺點越發明顯。解析法求解精度高，但需要大量的數學運算支持，這就使得可以快速得到機構設計參數的解析算法需求越發突出。

平面連桿機構的諧波特征參數方法是借助傅里葉級數理論，將連桿機構輸出運動采用傅里葉級數方法進行描述[2]。在此基礎上，借助快速傅里葉變換等數學工具，對連桿機構需要輸出的諧波特征參數進行分析，找到機構諧波特征參數與平面機構尺寸之間的關系，從而得到基于連桿機構輸出特征參數進行尺寸綜合的一般方法。

遺傳優化算法是一種基于生物自然選擇與遺傳機理的隨機與優化方法，在1950年代被提出后，鑒于其在求解復雜優化問題中的良好適應性，在工業設計領域被廣泛應用。 Deb等人提出NSGA-II(Non-dominated Sorting Genetic Algorithm 2)后，因其簡單、高效、解集收斂性好等優點，在多目標優化領域被廣泛應用。 孔民秀等[3]針對高速高加速度的平面并聯機構，基于NSGA-II算法來求解多目標優化問題，進行尺度綜合，提升了機構的動態性能。Baviskar等[4]提出了2種基于漸進式步長機制的算法，并與非支配排序遺傳算法的搜索方式相結合，通過控制步長和分割數目等參數，在子代中生成更好的染色體，實現了快速收斂。李新超等[5]針對NSGA-II算法中非支配排序耗時多的問題，提出了偏好順序淘汰的算法，減少了參與非支配排序解的數量,進而減少了求解時間，降低了偏好評價結果較差的個體解被選中后再進行交叉、變異的概率，提高了算法效率。

多目標遺傳優化算法滿足了多參數設計的要求，適用于求解較復雜的優化問題，但仍存在收斂速度慢、局部搜索能力不強、易陷入局部最優解等問題，不易得到穩定的全域最優解，且對算法初值敏感，對算法初值的依賴性較強。針對平面并聯五桿機構的設計問題，采用多目標遺傳算法計算最優解，算法初值問題是決定算法效率的重點。但在實際應用中，算法初值是不易確定的，造成了算法效率不高、收斂速度慢等問題。該項研究采用遺傳優化算法與諧波特征參數法相結合的方法，主要解決遺傳算法的初值問題、在初代搜索盲目、算法收斂速度慢的問題。

1平面五桿機構設計通用方程

平面五桿機構的諧波參數設計方法[6，7]，是在已知機構運動軌跡的情況下，無需建立特征庫及其他參數，用解析的方法來計算出符合目標運動軌跡特征的機構設計參數。諧波參數法分析中，可將平面五桿機構分解為2個二自由度的開鏈機構，即CBA和CDE在鉸點C處結合而成，可分解成2個鉸鏈二桿組進行分析，如圖1所示。

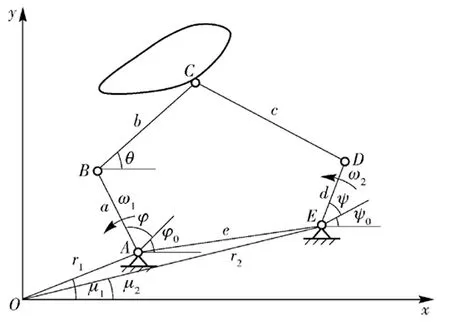
圖1 平面五桿機構二桿組示意圖

如機構在平面內向兩側方向運動軌跡對稱，則兩側桿組參數一致，只需計算其中一側桿組的參數即可。由諧波參數法的機構軌跡綜合設計方程[2]有：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

式中，j=0，1，…，n，j≠k,m2=0，±1，…，±k, …，±(n-j)

2五桿機構參數計算

確定五桿機構中C點的目標軌跡，并將目標軌跡根據實際需要離散為若干個點，將C點位于坐標系中的位置采用傅里葉形式表示。然后利用諧波參數法將C點目標軌跡中離散后的點計算得到目標軌跡點的諧波參數。將計算所得到的設計參數帶入平面五桿機構綜合設計方程中，得到符合機構目標運動軌跡的桿組設計參數。

3 NSGA-II多目標遺傳算法

NSGA-Ⅱ算法是在第一代非支配排序遺傳算法(NSGA算法)的基礎上改進而來，是在低維目標(2-，3-目標)優化問題中被應用最多的多目標遺傳算法，它主要降低了非劣排序遺傳算法的復雜性，相比NSGA算法具有運行速度快，解集收斂性好的特點。針對該項研究的三目標優化問題，NSGA-II算法相對適用。

NSGA-II算法中，初值的選擇尤為關鍵，它決定了整個算法效率和計算成本。本研究根據平面五桿機構的設計特點和諧波參數法得到的設計初值，為達到提高優化算法效率的目的，對NSGA-II算法進行了針對性調整，具體算法過程如下：

(1)根據諧波參數法得到的平面五桿機構的設計參數分別生成初代個體，將初代種群擴充至指定種群數；

(2)將個體的3個目標參數分別計算出對應數值解。將得到的解進行可行性篩選，留下可行解；

(3)尋找非支配解，并進行分層操作，將解分成若干層，進行快速非支配排序；

(4)將父代種群和子代種群合并，生成新的父代種群；

(5)進行實數編碼的二進制交叉操作；

(6)進行多項式變異，進行帶有偏好性的二進制錦標賽選擇；

(7)計算個體擁擠度；

(8)選擇合適個體組成新的父代；

(9)循環5～8步驟，直到進化至最大代數。

4算例

綜合平面五桿機構[7]，使平面五桿機構中C點在傳動比為1的條件下，實現如圖2所示目標運動軌跡。

圖2 平面五桿機構C點目標運動軌跡

將圖2所示的點用諧波參數法進行表示，然后得到目標軌跡的諧波參數，因涉及的五桿機構的目標運動軌跡對稱，故傳動比為1，根據目標軌跡的特征，計算得到C點目標軌跡的-4到4次諧波參數，如表1所示。

表1 目標軌跡的諧波參數

將計算所得到的諧波參數帶入平面五桿機構的綜合設計方程，可以得到符合目標運動軌跡的機構桿組設計參數，如表2所示。

表2 計算所得二桿組設計參數

將上述計算所得到機構桿組設計參數應用于NSGA-II算法中，生成算法的初代個體，為達到提高優化算法效率的目的，對NSGA-II算法進行了針對性調整，具體算法過程如下：

(1)依據表2中計算所得的4組設計參數分別生成初代個體，并將初代種群擴充至指定種群數；

(2)將主動臂扭矩T、主動臂轉角A、機構慣量IM，3個參數分別計算出對應數值解。將得到的解集進行可行性篩選，留下可行解；

(3)尋找非支配解，然后進行分層操作，將解分成若干層，進行快速非支配排序；

(4)將父代種群和子代種群合并，生成新的父代種群；

(5)進行實數編碼的二進制交叉操作；

(6)進行多項式變異，然后進行帶有偏好性的二進制錦標賽選擇；

(7)計算個體擁擠度；

(8)選擇合適的個體組成新的父代；

(9)循環5～8步驟，直到進化至最大代數。

其中，第(6)項中的偏好性選擇，是根據計算所得的初值中主動臂與從動臂的長度，在主動臂及從動臂之和的總長度變化不超過5%的條件下，分別向增長與縮短2個方向變異，如主動臂長度增加，則從動臂長度減小。

4.1 平面五桿機構優化模型

設計變量：x、y、u、v、w，目標函數：

(10)

約束條件：

(11)

本算例的目標函數采用主動臂扭矩T、主動臂轉角A、機構慣量IM，3個參數原因的如下：

(1) 主動臂扭矩T：在機構設計中，主動臂扭矩值關系到驅動電機的選取范圍問題，電機扭矩范圍又與電機的體積相關，電機體積又與兩個主動臂間距相關，主動臂間距與機構的尺寸相關。所以，在五桿機構設計中，要盡可能的降低主動臂扭矩，以利于減小機構的體積，并降低電機選用要求；

(2) 主動臂轉角A：在平面五桿機構設計重，尤其是有副桿的平面五桿機構設計中，需要避免機構桿組之間的干涉，這就使得主動臂轉角范圍相較理論值相應減小，所以在機構設計是需要盡量降低主動臂轉角范圍，在設計完成后進行仿真確認。同時，在高速機構設計中，降低了主動臂轉角范圍，會對機構的響應特性有正面影響；

(3) 機構慣量IM：在高速運動環境中，機構慣量需要滿足一定設計要求，若機構的慣量過大，容易造成高速運動機構失效。機構慣量對機構的動態響應特性也有影響，在高速運動機構應用中要求機構慣量要盡量小，以提高機構的動態響應特性。

4.2 運行結果

由NSGA-II算法得到的Pareto最優解如圖3所示。

圖3 Pareto最優解

表3 多目標優化結果

5結論

(1)將平面五桿機構的諧波參數法與NSGA-II遺傳優化算法相結合，對遺傳算子加入偏好性選擇，可以得到一個基于機構工作空間，不需要設計初值的多目標遺傳優化設計方法，既滿足了機構高速運動要求，同時又滿足了機構驅動關節的低扭矩要求，且滿足了平面機構的高響應特性要求。

(2)本設計方法所涉及的算法，根據機構的工作空間，可以單獨計算出單個設計參數的范圍，以供設計者參考。使設計者在選用驅動單元、確定機構運動節拍、設計機構強度等參數時提供可靠的取值范圍，還可以根據具體設計要求，指定其中某個設計參數的優先級，使設計者在機構設計計算中，可以根據不同設計要求采用更加靈活實用的計算模型。

(3)應用諧波-多目標遺傳優化算法后，程序的運算時間由無固定初值時，在300～400代左右收斂，運行時間為30～40 h，對比由諧波參數法計算遺傳算法初值并生成初代個體值，對遺傳算子進行偏好性改進后，算法在100～150代左右收斂，運行時間為12～18 h，算法效率可以提高50%以上。諧波-多目標遺傳優化算法在解決了遺傳算法的初值問題后，算法效率得到了大幅度提升，在平面五桿機構的設計中，提供了更為快速有效的解決方案。