基于改進PSO-BFO算法的WSN節點覆蓋優化

龔瑞昆，鄧朋浩

(華北理工大學 電氣工程學院，河北 唐山 063210)

隨著科技高速發展，無線傳感器網絡(WSN)憑借出色的性能優勢，被廣泛應用于眾多領域，其中節點部署設計是WSN中的關鍵問題。在實際應用中，由于部署方式存在局限性，造成網絡覆蓋率低、資源浪費。設計合適的節點部署方式，能有效提高傳感器的監測效率和網絡中數據傳輸質量。

近年來，很多學者對WSN網絡的覆蓋優化方法進行了大量研究：文獻[1-3]均提出改進的粒子群算法，對于慣性權重系數進行線性調整，收斂速度加快，但是由于粒子種群的種類比較單一，需要大量數目的粒子，容易造成覆蓋區域重疊；文獻[4]中宋婷婷，張達敏等人提出出改進的鯨魚優化算法，在搜索階段引入自適應步長，加快收斂速度和尋優效率，但是不能完全覆蓋，留有覆蓋空洞；文獻[5]文森提出將粒子群算法和Voronoi圖理論相結合，有效修補覆蓋漏洞問題，但尋優效率并不十分高效；文獻[6]梁櫻馨提出基于PSO的改進細菌覓食算法，有效避免因"早熟"導致的局部最優現象，覆蓋重疊區域以及盲區有所減少；文獻[7,8]分別提出改進的果蠅優化算法和人工蜂群算法，縮短搜索時間，減少網絡冗余度，但是隨著傳感器節點數目的增加,節點利用率逐漸減小；文獻[9]中張雪，秦宇祺，張倩倩等人提出改進的自適應灰狼算法，引入非線性收斂因子和自適應調整策略，克服了容易陷入局部最優的缺點，但是在處理多模態測試函數時效果較差；文獻[10]提出差分演化和粒子群優化算法，前期加強PSO的全局搜素能力，后期充分利用差分演化算法增強局部搜索能力，提高了尋優效率。

針對上述不足，該項研究提出一種基于改進PSO-BFO算法的WSN節點覆蓋優化方法，該方法在解決WSN區域覆蓋問題上，能夠取得較好效果，與其他算法相比，其收斂速度更快，網絡覆蓋率更高，實驗結果證明改進PSO-BFO算法更具優越性。

1 WSN節點覆優化模型

假設監測區域是一個二維平面,數字化為M×N個網格點，在區域內部署Z個傳感器，所有傳感器具有相同的感知半徑R和通信半徑Rs，且Rs≤2R。在仿真中使用0-1感知模型，把傳感器感知區間抽象成為一個"圓盤"，假設傳感器節點Ai的坐標為(xi，yi)，目標Bj的坐標為(xi，yi)，兩點之間的距離為：

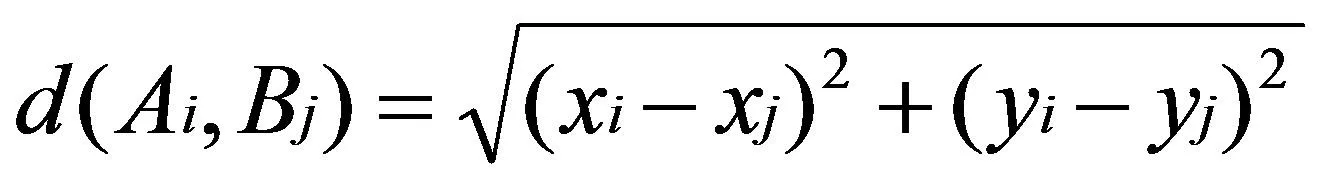
(1)

如果目標b在圓盤內，被傳感器節點a感知到的概率為P(a,b)=1，否則 ，可用數學表達式(2)表示：

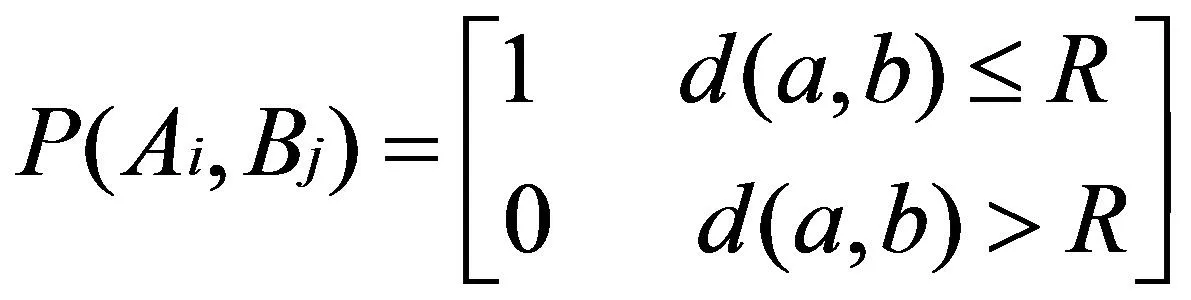
(2)

由于目標不容易被感知到，為了提高感知概率，需要多個傳感器共同監測，則目標b被傳感器節點集合G感知到的概率為：

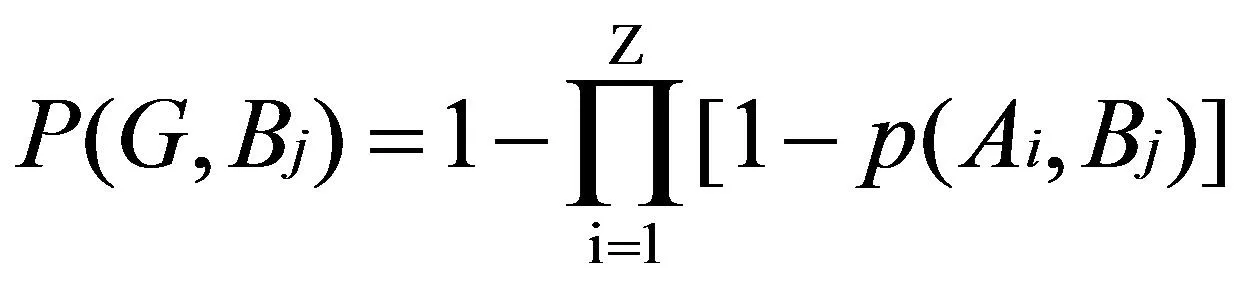
(3)

監測區域的覆蓋率定義：

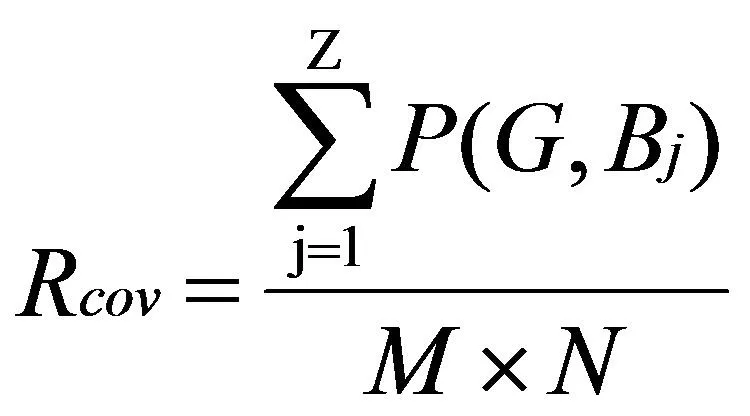
(4)

公式(4)是WSN節點覆蓋優化模型目標函數，用改進的PSO-BFO算法求Rcov的最優值以提高覆蓋質量。

2改進PSO-BFO優化算法

2.1 標準粒子群算法(PSO)

粒子群算法(PSO)是受集群動物啟發而開發的一種智能算法，通過群體中的個體對信息的共享來使整個群體的運動實現對解空間的全局搜索。它最優越的地方是具有記憶能力，能記憶保留個體和群體的信息。

設粒子群空間有m個粒子，空間為D維，每個粒子都有一個初始位xi=(xi1,xi2,…,xid)T，都存在初速度向量Vi=(Vi1,Vi2,…,Vid)T，其中i={1，2，3…，m}。在算法優化過程中，會形成局部最優解pbesti和全局最優解gbest，粒子的飛行速度Vi根據2個最優解進行動態調整，直到粒子圍繞一個最優點聚集。其中粒子速度和位置更新公式為；

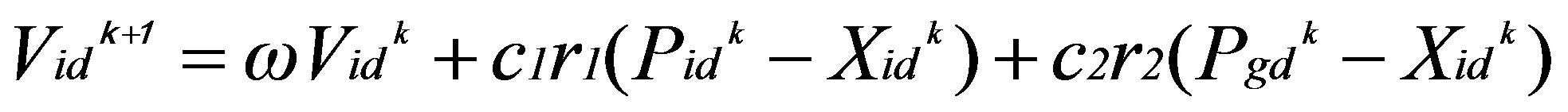
(5)

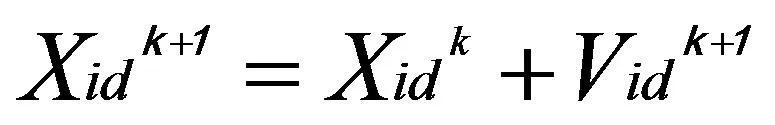
(6)

其中，ω是慣性權重系數，C1、C2是學習因子，r1、r2是[0,1]的隨機數，k為迭代次數。XidK和Vidk分別為粒子位置和速度。

2.2 改進粒子群算法

通過觀察粒子運動速度公式可知，ω能調節PSO的搜索能力，但是只是隨著迭代次數線性減小，實時性較差。所以在PSO算法的慣性權重系數中引入進化因子和聚合因子，增強粒子的自適應能力。

2.2.1 進化因子和聚合因子

設粒子第k次迭代后的函數值為f(xik)，局部最優函數值為f(Pidk),全局最優函數值為f(Pgdk)。

對進化因子的定義如下所示。粒子i的進化程度定義為：

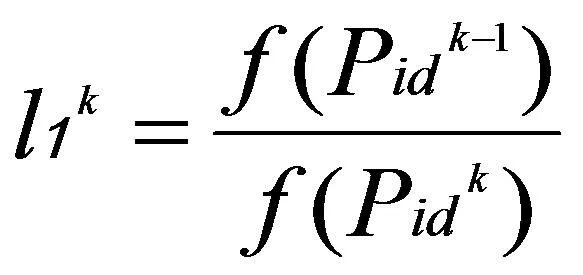
(7)

粒子群局部最優平均函數值的進化程度定義為：

(8)

粒子群全局最優平均函數值的進化程度定義為：

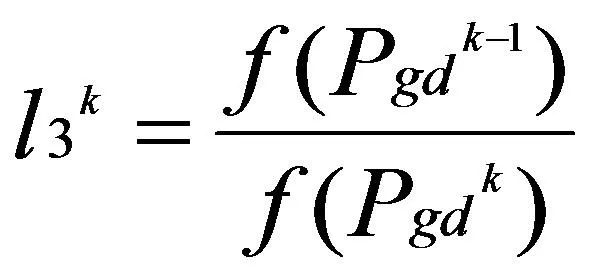
(9)

所以第k次迭代的進化因子可以表示為：

(10)

其中a1，a2，a3是[0,1]的系數且a1+a2+a3=1。

對聚合因子的定義如下所示,粒子的局部最優平均函數值定義為：

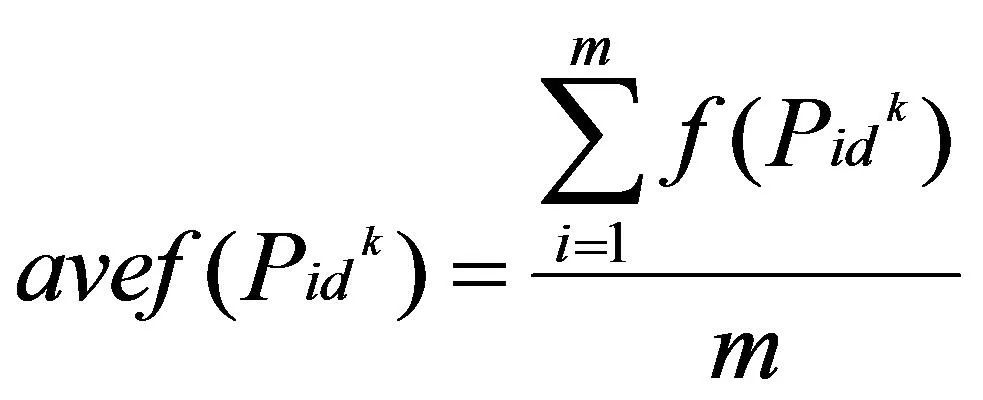
(11)

定義第k次迭代后，粒子平均函數值為：

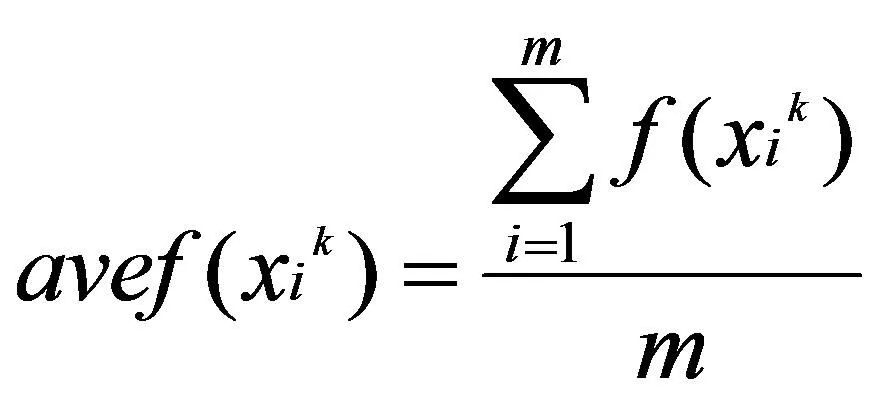
(12)

聚合程度其實就是當前粒子的平均函數值與局部最優平均函數值的接近程度，如公式(13)所示：

(13)

2.2.2 自適應慣性權重系數

根據引入的進化因子和聚合因子，自適應慣性權重系數公式可以定義為下式：

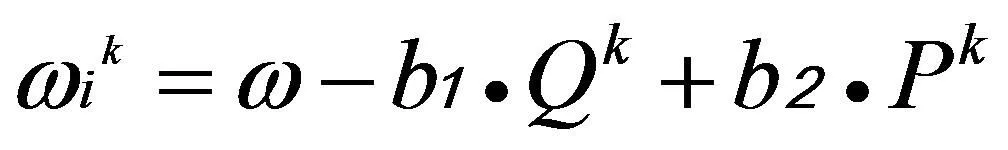
(14)

其中ω為初始慣性權重系數b1，b2，b3為調節系數，且b1+b2=1。Qk較大時，表示粒子進化速度緩慢，Pk較大時，表示粒子群的聚合程度較高。將自適應慣性權重系數代入公式(5)可得更新公式為：

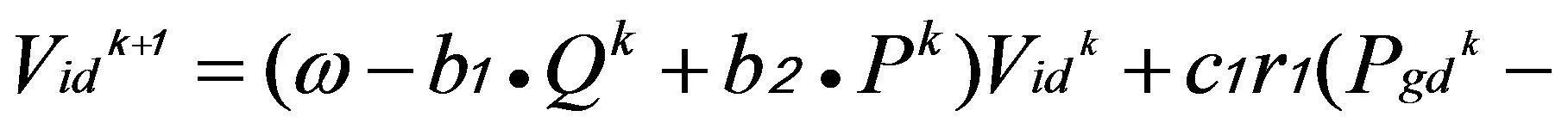
(15)

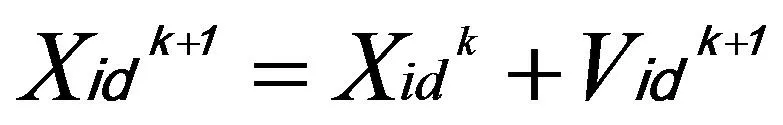
(16)

2.3 細菌覓食算法(BFO)

細菌覓食算法(BFO)是受細菌生長繁殖規律啟發提出的一種新型仿生算法，算法簡單、靈活，具有很強的魯棒性和適應性，而且可以與其它各種算法結合生成新的算法，應用于不同的領域。BFO算法主要是通過趨化、聚集、復制和遷移4個操作來進行搜索尋優。操作如下：

趨化操作：細菌通過翻轉和前進向富養區域聚集，位置更新公式如下所示：

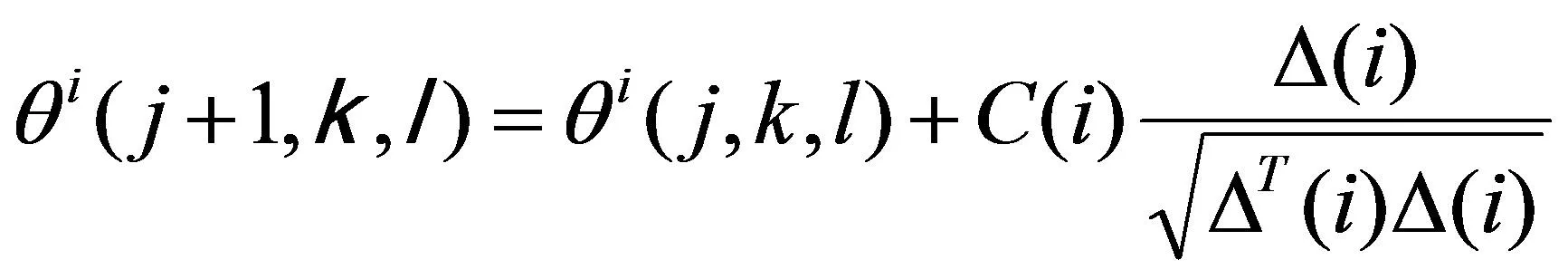
(17)

聚集操作：細菌之間會有信息交流，會通過釋放引力和斥力信號來促使細菌聚集在一起，可通過修正細菌適應度函數來達到目的。細菌的適應度函數如下所示：

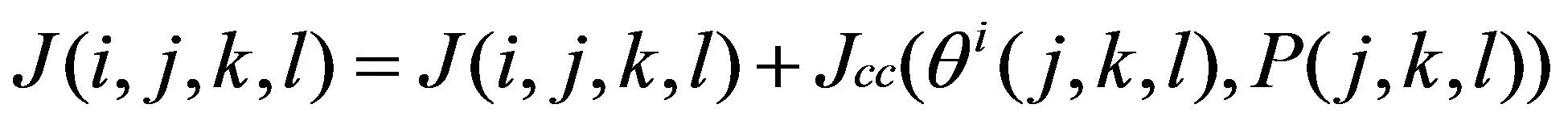
(18)

復制操作：對細菌的適應度函數值進行排序，活性好的細菌進行分裂復制，分裂所得細菌具有與母菌相同特性。

遷移操作：當環境發生改變或者其他突變情況，區域內的細菌會發生死亡或者遷移到其他地方。

2.4 改進細菌覓食算法

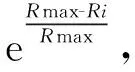
《蘭納克》是一次尋根之旅，是一個民族主義者和小說家表達對本民族命運關切的特有方式，同時它也是一個政治諷喻，以魔幻現實主義的方式呈現了內受經濟衰退困擾、外逢強權政府壓制的蘇格蘭社會狀況，它更是整個西方工業社會的寫照，揭示了現代城市生活各種狀況的根源。在這部具有強烈“反烏托邦”色彩的小說中，格雷以諷刺的手法表達了對個人命運的關切和對社會政治經濟的不滿，批判了整個西方的政治意識形態。

(19)

其中，Rmax表示算法最大迭代次數，Ri表示細菌i當前迭代次數。自適應調節游動步長，改進后的細菌位置更新公式為：

(20)

2.5 改進PSO-BFO算法

PSO算法全局搜索能力強，但在搜索過程中容易陷入局部最優，BFO算法擁有較強的局部搜索能力，改進趨化操作中的搜索步長又極大提高了搜索過程中最優解的準確性。將BFO算法引入PSO算法中，用BFO中θi′(j+1,k,l)替代PSO中粒子所在位置Xidk，改進后的公式為：

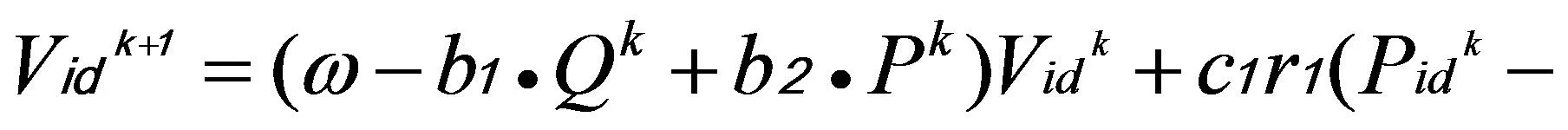
(21)

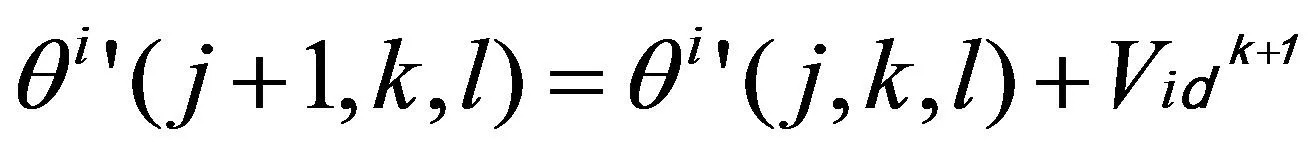
(22)

綜上所述，改進PSO-BFO算法的基本思想是：前期采用PSO算法對監測區域進行全局搜索，通過PSO算法中的式(15)、式(16)跟蹤粒子群的速度和位置，尋找全局最優解，尋找到當前pbest和gbest；后期的局部搜索則由BFO算法進行，通過式(21)、式(22)對區域進行局部搜索，提高PSO的局部搜索能力。2種算法優勢結合，共同完成對監測區域的搜索。流程圖如圖1所示，算法主要步驟如下：

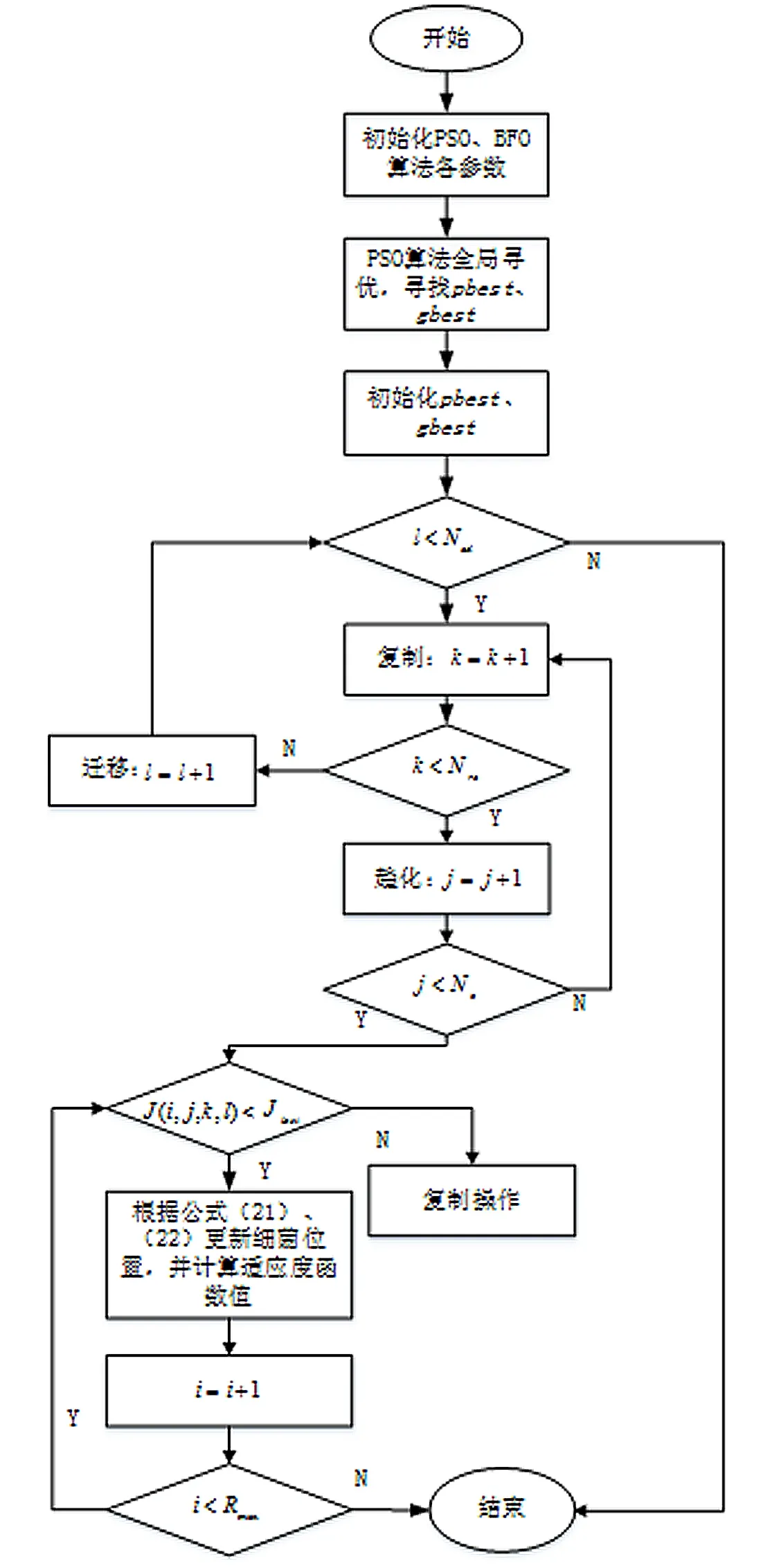
圖1 算法流程框圖

(1)初始化PSO、BFO算法中的各種參數；

(3)細菌翻轉尋找局部最優，根據式(21)、式(22)更新細菌動態，并計算適應度函數；

(4)比較細菌的適應度函數值，當前值如果小于上一次的值，則返回步驟(3)，如果大于則進行下一步；

(5)趨化操作循環；

(6)聚集操作循環；

(7)復制操作循環；

(8)遷移操作循環；

(9)判斷是否達到最大迭代次數，如果達到，結束算法；否則返回步驟4。

3仿真與性能測試

3.1 覆蓋優化性能測試

通過在MATLAB中實驗仿真，比較BFO算法、WOA算法和改進的PSO-BFO算法的節點覆蓋效果。設置監測區域為20 m×20 m的二維平面，傳感器節點設置為24個，感知半徑為2.5 m，通信半徑為5 m，迭代次數為100次。圖2為3種算法的迭代曲線，圖3為傳感器節點隨機分布圖，圖4為BFO算法單獨使用時的節點優化分布圖，圖5為WOA算法優化的節點分布圖,圖6為改進PSO-BFO算法優化的節點分布圖。

圖2 3種算法的迭代曲線

圖3 傳感器節點隨機分布圖 圖4 BFO算法單獨使用時的節點優化分布圖

圖5 WOA算法優化的節點分布圖 圖6 改進PSO-BFO算法優化圖

通過圖2可以比較出BFO算法、WOA算法和改進PSO-BFO優化算法對傳感器節點部署的優化效果。該研究算法的覆蓋率可達到97.5%，對比BFO算法的覆蓋率92.7%，WOA算法覆蓋率90.7%，覆蓋率上升了4.8%和6.8%；觀察傳感器節點覆蓋圖可以發現，BFO和WOA優化算法雖然改善了一些傳感器重疊問題，但還是存在覆蓋不均勻，覆蓋空洞的問題，而基于改進PSO-BFO優化算法的效果就比較理想，監測區域覆蓋比較全，極大地改善了區域聚集重疊的現象，減少了資源浪費。

3.2 收斂性能測試

使用3種經典測試函數Griewank、Rosenbrock和Rastrigrin函數分別對BFO算法、WOA算法和改進PSO-BFO算法進行收斂性測試比較，其中以Griewank函數為例進行說明。Griewank函數為典型的多模態函數，二維圖像如圖7所示。Griewank函數數學表達公式如(23)所示：

圖7 Griewank函數圖像

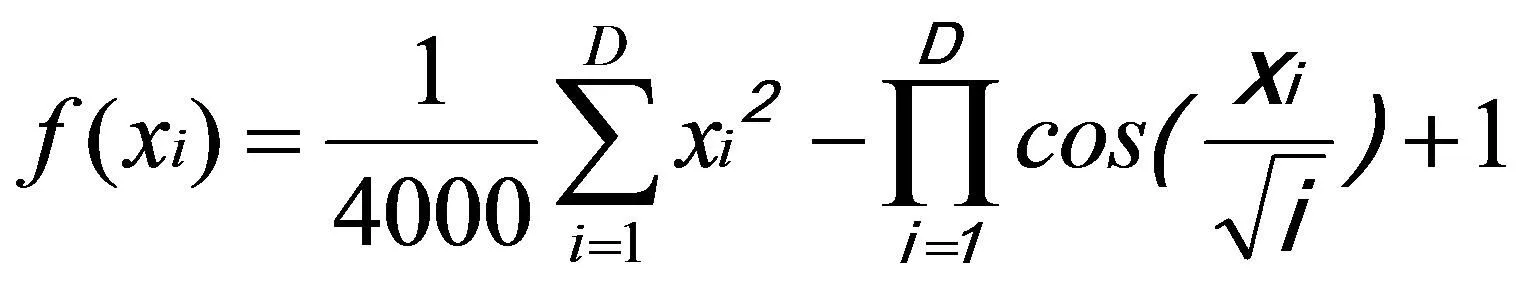
(23)

經過多次重復測試，改進混合算法PSO-BFO通過結合改進BFO算法和PSO算法的全局和局部搜索能力，有效避免陷入局部最優，極大加快粒子的收斂速度，其收斂效果優于BFO算法和WOA算法。收斂效果測試如圖8所示。

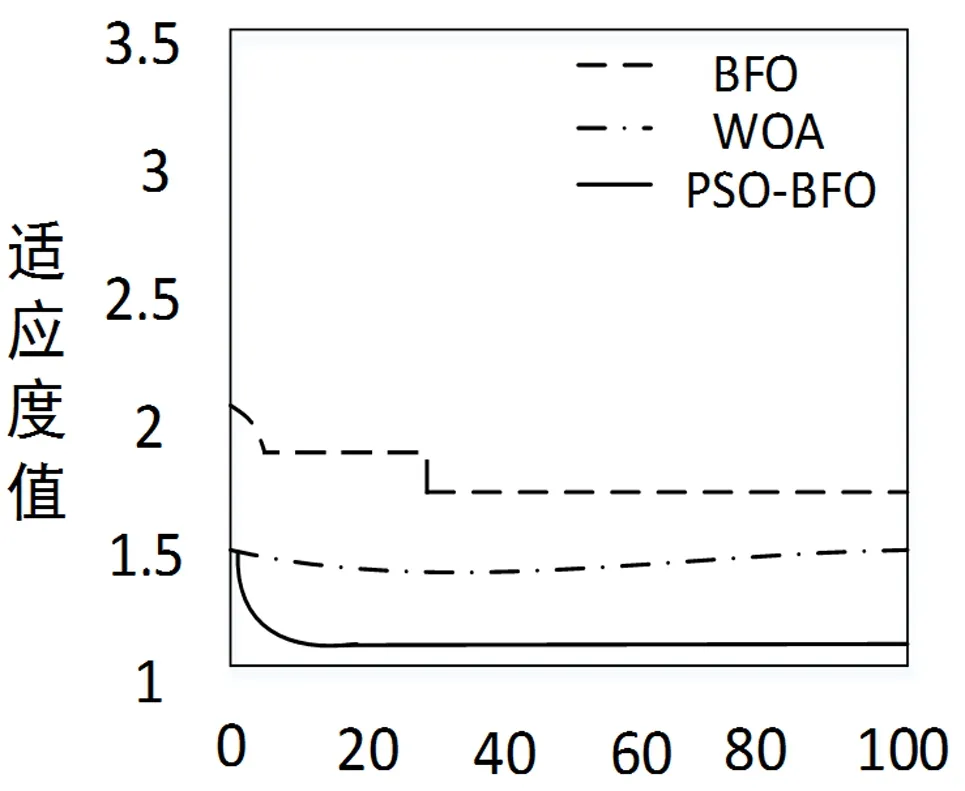
圖8 迭代收斂效果測試

另外分別使用經典函數Rosenbrock和Rastrigrin函數對3種算法進行收斂性測試，3種函數測試結果如表1所示。

表1 3種算法的收斂效果

4結論

(1)該研究算法在解決傳感器節點部署問題上更加高效，收斂速度更快，網絡覆蓋率更高，有效地減少了節點重疊聚集現象，減少了資源浪費。

(2)PSO-BFO算法也存在一些缺點，比如算法中參數較多，影響算法收斂速度，需要選擇合適的參數才能最高發揮算法的性能。