基準偏移在尺寸鏈公差累加計算中的作用及計算結果六西格瑪意義的實踐

黃恭勤，田立群

（安波福電子（蘇州）有限公司, 江蘇 蘇州 215126）

0 引言

機械工程師在設計與研發工程中，需要為關鍵特征設定公差范圍；然而這些公差是否可以滿足功能要求，就需要進行尺寸鏈公差累加計算分析。當尺寸特征控制框中包含基準偏移的時候，如何帶入這些偏移的影響，以及如何評估計算分析結果的六西格瑪的意義，就會成為工程師需要面對的問題。

1 飾件組裝及其圖樣案例

1.1 案例介紹

如圖1所示，3個襯板（襯板1、襯板2和襯板3）裝配在面板上。現在需要探究襯板3和面板之間上部的間隙大小。

圖1 面板和3個襯板的組裝

圖2所示為面板標注圖，由于襯板3和襯板2，以及襯板2和襯板1之間的間隙也需要探究，所以襯板3在面板上的定位孔以襯板2在面板上的定位孔為基準被控制位置度；襯板2在面板上的定位孔以襯板1在面板上的定位孔為基準被控制位置度；從制造工藝的角度出發，面板上側輪廓度以下側孔B和腰槽C為基準控制[1]。由于面板使用多個固定尺寸功能檢具（fixed-size functional gage）檢測關鍵尺寸和公差，特征控制基準普遍使用了基準偏移（標注表現為基準后面有@MMB標記）。

圖2 面板公差標注圖

圖3所示為襯板3標注圖。類似于面板，輪廓度的控制也使用了基準偏移（標注表現為基準后面有@MMB標記）。

圖3 襯板3的公差標注圖

1.2 初步尺寸鏈公差累加計算

為了探究圖1 中間隙的大小，進行了初步的尺寸鏈公差累加計算，結果為: Max（最大值）=2.9，Min（最小值）=1.8。然而在所有部件被檢測合格的情況下，部件裝配后間隙有時卻在1.8～3.0范圍之外。這是部件檢測的過程出現了問題，還是尺寸鏈公差累加計算出現了錯誤？后經研究發現，所有部件檢測的過程中都正確地使用了固定尺寸功能檢具進行了可靠的檢測；然而,在初步的計算中卻忽略了所有的基準偏移在公差累加計算中的作用（即所有的圖樣中基準符號后面的@MMB都被忽略了）。這樣產生如下的問題：在這個案例中，基準偏移在公差累加計算中的作用到底有多大？其作用或者影響是否可以被忽略？

2 使用雙列累加計算方法重新進行尺寸鏈公差累加計算

為了解決上面的問題，使用雙列累加計算方法（Two Column Stack Method）對這個案例進行了重新的計算。累加計算尺寸鏈如圖4所示。計算間隙為襯板3和面板間的間隙。因為3個襯板在裝配的時候都需要另外安裝其它的有相當質量的部件，所以尺寸鏈考慮了重力的作用；在此前提下，這個尺寸鏈圖可以同時計算出間隙的最大值和最小值。

圖4 尺寸鏈圖

雙列累加計算方法（Two Column Stack Method）計算過程如圖5所示。

雙列累加計算方法主要特點為：不同于使用外部邊界（OB）和內部邊界（IB）追究單個特征對象極限邊界進而展開計算的比較具有一般性的方法，位置度和輪廓度的值被細分。例如位置度的值被細分為3項：1）特征控制框內數值；2）位置度補償值（Bonus）；3）位置度基準偏移值（Datum Shift）。例如圖5中G、H、I行和K、L、M行。

因為值被細分，各個量就可以被細致地追究。例如圖5中G,H,I行:

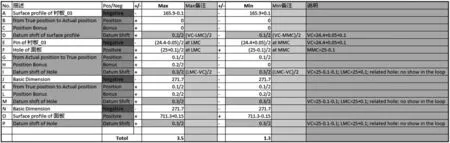
圖5 雙列累加計算方法過程圖

1）行G取決于對應孔的位置度數值0.1，0.1/2被填入最大值列及最小值列（在這里，因為尺寸鏈向量經過的是孔半徑，所以表格數值取用0.1/2）;

2）行H的取值相關于行F對應孔的取值，因為行F最大值列取值（25+0.1）/2為最小材料狀態，所以行H最大值列的取值為0.2/2（即（LMC-MMC）/2），而行F最小值列孔取值為孔最大尺寸狀態（MMC），所以行H最小值列取值為0（MMC沒有Bonus）;

3）行I錄入的數值為對應孔的基準偏移量，而這個基準為基準D及基準E對應的孔和腰孔。在尺寸鏈中這個孔及腰孔對應的尺寸大小并沒有出現，那么無論對于求解間隙的最大值還是最小值，這行的偏移量都應該錄入偏移量的最大值[2]。故對于基準D及基準E對應的孔和腰孔：VC=25-0.1-0.1；LMC=25+0.1（VC為Virtual Condition，即實效狀況）；Datum shift=(LMC-VC)/2=0.3/2=0.15。

面板諸多特征孔垂直度的意義被包含在對應的其他尺寸或者位置度或輪廓度中，它們（垂直度等）對于此尺寸鏈公差累積計算過程不產生影響。

對于行H，如果對于求解最大值和最小值，都填入了0.2或者0，皆是在計算中帶入了一個錯誤：額外帶入一個不存在的量或者遺漏一個量；對于行I，對應孔或者腰孔的尺寸并沒有出現，追究相應孔的外部邊界及內部邊界的算法就不再適用。從本案例可以看出，雙列累加計算方法（Two Column Stack Method），對于位置度和輪廓度控制擁有補償量（Bonus）和基準偏移量（Datum Shift）的案例非常適用，分析過程緊隨GD&T的固定尺寸功能檢具意義，解算過程清晰明了；分析結果明確可信，無爭議。當然這個方法也有它本身的缺點，即計算過程相對復雜，使用Excel等工具實現求解邏輯的過程相對困難，對分析操作者對于GD&T及固定尺寸功能檢具意義的理解程度提出了更高的要求。

按照這個方法，最后解算的結果為：最大值為3.5，最小值為1.3。這個結果和初步累加計算的結果（Max=2.9，Min=1.8）比較，差別明顯很大；很顯然，如果這個差別被忽略，進而產生的工程風險是相當大的。

3 雙列累加計算方法結果六西格瑪意義的實踐

上述雙列累加計算方法產生的結果，體現了極端的情形（Worst case situation）的分析意義。也就是對于本案例，當各個部件都通過檢測的情況下，部件組裝后的被分析的間隙是不會超出計算結果（最大值為3.5，最小值為1.3）的。這個結果關注的是工程風險最低的安全性，然而卻忽視了風險概率的意義。也就是從六西格瑪的立場來講，一般情況下，工程師根據統計學的實踐意義會關注六西格瑪理論下的極值（最大值和最小值）。

上述陳述對應的實際情況為：當個別部件有少量超差的時候，我們會希望得出基于六西格瑪的極值，繼而判斷這個少量超差會使結果突破目標要求，還是概率意義上風險可控。

一般來講，在考慮六西格瑪意義的時候，根據經驗，經常是將各個公差取平方后求和，然后開平方根，再乘以一個修正系數（一般為1.5），進而獲得最大值和最小值。然而這個方法在面對上面的計算過程時，會變得繁瑣，并且根據經驗很容易降低結果可靠性。這時候，是否有一個更為簡明和可靠的方法可以實現六西格瑪的實踐意義？

如圖6所示，在六西格瑪質量水平的要求下（考慮了正態分布1.5倍標準差的偏移），總缺陷概率為3.4×10-6而上述案例結果（最大值為3.5，最小值為1.3）為不考慮概率意義的分析結果，它的缺陷概率理論上為0；0缺陷的意義在統計學的理論來講即為7西格瑪的水平[3]。所以我們可以直接將上述結果定義為7西格瑪的結果。根據這個理論解讀，可以計算標準差的大小：標準差=(Max-Min)/14=（3.5-1.3）/14=0.157。

圖6 雙列累加計算方法結果六西格瑪意義

這樣，如果目標西格瑪水平被定位在5西格瑪的話，上面分析結果即為：最大值=3.2，最小值=1.6（Max=3.2,Min=1.6）。這樣，大概單邊0.3雙邊0.6的公差范圍被研發人員獲得。在當前競爭嚴酷、品質追究嚴厲的行業背景下，上面的公差范圍是非常珍貴或者具有決定性的。

4 基準偏移在尺寸鏈公差累加計算中的作用及計算結果六西格瑪意義的實踐總結

在不同行業或者情況下，尺寸鏈公差累加計算具體操作方式和方法是不盡相同的。對于相對規整、部件形狀和部件間組裝關系基本表現在正交關系的時候，可以借助Excel表格或者類似的二次開發工具展開累加計算；對于部件形狀復雜、基準特征及部件間關系為空間自由形狀（即不再是正交關系）的案例，借助基于3D CAD環境的專業TSU軟件可能會是必要的選擇。對于本文出現的案例，部件間基準和被控制特征基本屬于正交關系，同時基準偏移的影響對于結果的影響達到了不可以被忽略的程度，這時候本文提供的雙列累加計算方法（Two Column Stack Method）無疑可以作為這樣情況下最佳的公差累加計算解決方案。

對于各種公差累加計算結果六西格瑪意義的實踐，不同算法條件下的表現形式經常是有所不同的。基于上文闡述的雙列累加計算方法所具有的細化無爭議的特點及六西格瑪的理論意義，本文提出的求解標準差的方法簡明、易于操作，有利于工程師在實踐工作中爭取產品成本下降空間，有助于使研發過程確保立于不敗之地。