一種改進的差分隱私參數設置及數據優化算法 *
胡雨谷,葛麗娜,2
(1.廣西民族大學人工智能學院,廣西 南寧 530006;2.廣西民族大學網絡通信工程重點實驗室,廣西 南寧 530006)
1 引言
大數據、物聯網規模與日俱增,全球參與設備的數量數以億計。每個連接到互聯網的設備或多或少不斷地產生著各種各樣的數據,其中可能含有用戶的隱私信息。當包含隱私數據的設備接入互聯網并提供數據給其他設備訪問時,用戶的隱私便存在被暴露的風險。如何控制和協調產生數據的設備與訪問數據的設備之間的訪問是一個難點。因而構建安全可用的數據訪問處理方法是實現數據訪問控制的重要研究方向之一。Dwork[1]提出的差分隱私DP(Differential Privacy)有著嚴格數學證明,其隱私預算參數ε改進了傳統隱私保護模型需要背景知識假設和無法定量分析隱私保護水平的不足,從而能夠對數據的隱私安全提供良好的保障。
文獻[2]利用概率知識,給出了一種基于背景知識的攻擊模型,并計算出差分隱私預算ε的上限。文獻[3]則基于Laplace機制,對差分隱私的結果進行查詢分析,并依據結果推導數據集中是否含有攻擊對象,繼而得出攻擊者的成功概率和優化的差分隱私預算ε的上界。文獻[4]提出啟發式策略LPBDP(Limit Privacy Breaches in Differential Privacy),使得隱私參數ε的設置不再依賴于經驗或實驗,而是可以根據查詢值的先驗概率與后驗概率進行啟發式設置。文獻[5]研究了選擇差分隱私預算ε和δ時必須考慮的關鍵因素,提出了一個簡單的經濟模型,使差分隱私用戶能夠根據實際可估計的量,有原則地選擇差分隱私預算參數。文獻[6]則在文獻[4,5]的基礎上,依據置信分析過程,設計了差分隱私預算配置算法。
現有的研究大都集中在對公式理論的改進,忽視了實際的應用場景,往往不能很好地從數據的使用者和數據的提供者角度著手,去滿足現實隱私的需求。
本文充分考慮應用場景,根據數據訪問者和貢獻者的信譽度信息,并與數據隱私度以及訪問權限值關聯,設計了基于信譽的差分隱私參數設置算法RBPPA(Reputation for differential privacy Based Privacy Parameter setting Algorithm),實現了細粒度的隱私參數設置。針對滿足隱私保護的加噪數據可用性降低的問題,設計了基于平方根無味卡爾曼濾波的差分隱私數據優化算法DPSRUKF(Differential Privacy data optimization algorithm based on Square-Root Unscented Kalman Filter),對加噪數據進行優化[6,7],以提高差分隱私數據的可用性。
2 差分隱私的隱私參數設置算法
本文所提出的算法基于如下應用場景:用戶甲的設備產生了一些數據,并有選擇地向其他設備開放數據的訪問權限,下文稱為數據貢獻者DC(Data Contributor);用戶乙、丙和丁等眾多用戶需要訪問用戶甲的設備產生的數據,下文稱為數據訪問者DV(Data Visitor)。圖1所示為本文所提算法的應用場景示意圖。
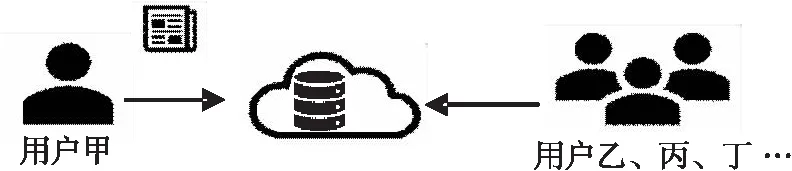
Figure 1 Application scenarios圖1 應用場景示意圖
面對這樣的場景,從數據貢獻者DC的角度出發,首先會考慮自身數據的安全性,通過差分隱私技術提供數據隱私的保護;從數據訪問者DV的角度出發,首先會考慮所請求的數據的完整性、可用性等。為此,綜合兩者的利益,基于兩者的信譽度設計細粒度的隱私參數設置算法,實現了在使用敏感數據時保證其隱私得到保護。
2.1 差分隱私
差分隱私在強大的數學模型基礎上嚴格定義了攻擊模型,對隱私泄露給出了嚴謹、定量化的表示和證明,使得人們可以對不同參數下的數據集的隱私保護水平予以評估和比較。差分隱私有2個最基本的實現機制,針對數值型數據采用Laplace機制,而針對非數值型的數據可采用指數機制[8]。
定義1(差分隱私) 設給定一個隨機隱私函數M是滿足(ε,δ)-差分隱私的,如果2個數據集D1和D2之間只相差1個元素,即‖D1-D2‖1≤1,對所有S?Range(M),有:
Pr[M(D1)∈S]≤eε·Pr[M(D2)∈S]+δ
其中,Pr[·]為概率表示,ε為隱私保護的預算值。其中,若δ=0,稱算法M滿足(ε,0)-差分隱私。
定義2(Laplace機制) 對于任一函數f:N|χ|→Rk,Laplace機制定義如下:
ML(x,f(·),ε)=f(x)+(Y1,…,Yi,…,Yk)
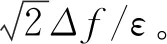
根據定義1可知,對僅有1個元素不同的相鄰數據集,隨機算法M的輸出結果由隱私預算ε和參數δ決定。ε越小,其隱私保護程度越高,當ε=0,δ=0時,有:
Pr[M(D1)∈S]≤e0·Pr[M(D2)∈S]+δ?
Pr[M(D1)∈S]≤Pr[M(D2)∈S]+δ?
Pr[M(D1)∈S]=Pr[M(D2)∈S]
因此,ε=0,δ=0時,M對D1和D2的查詢結果完全相同,數據的可用性完全喪失。
2.2 隱私參數設置算法
本文的隱私參數設置算法是在李森有等人[9]的研究基礎上改進與完善的,通過對數據共享者與數據訪問者的信譽度值、數據貢獻者對數據隱私安全級別的設置值,動態確定數據訪問者查詢數據獲得的安全可信度等級,以獲得相應的隱私保護預算,實現細粒度的訪問控制。
為了實現數據貢獻者的隱私數據安全,同時使數據訪問者最大化地利用共享數據,基于數據貢獻者與數據訪問者的信譽度,本文提出了差分隱私參數設置算法RBPPA。RBPPA的組成結構如圖2所示,表示了數據訪問控制的信息流向。
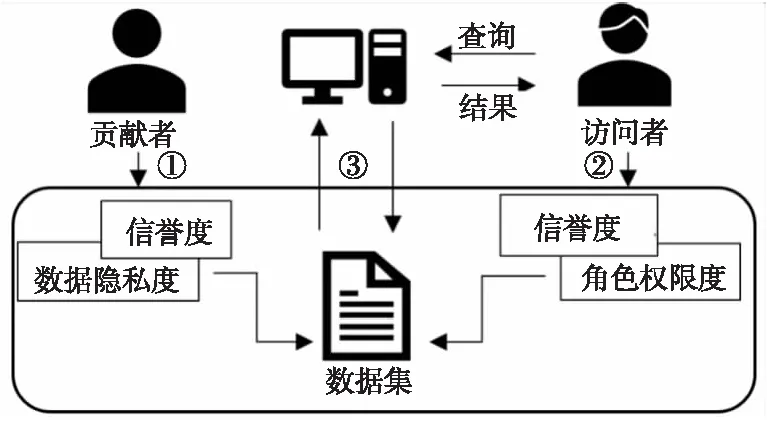
Figure 2 Composition of RBPPA圖2 RBPPA的組成結構
(1)讀取數據貢獻者的信譽度,設定其貢獻的數據隱私保護度的值;
(2)讀取數據訪問者的信譽度,找到其角色屬性相應權限度的值;
(3)利用(1)與(2)得到的數值,計算數據的隱私保護預算值ε,進一步計算其加噪后的數據值。
RBPPA算法中,對數據查詢的可信度由數據訪問者與數據貢獻者雙方的信譽度共同決定,他們的信譽度值越大,就能夠查詢到越接近真實值的數據;同時,數據貢獻者有對所貢獻數據設置隱私保護程度的權力,其值越低則可查詢到的數據越接近真實值。
首先,計算查詢安全可信度QC(Querying security Credibility)和數據貢獻者可信度 :
查詢安全可信度QC由數據訪問者的可信度DVC(Data Visitor Credibility)和數據貢獻者的可信度DDC(Data Dedicator Credibility)通過加權計算而得,即QC的計算方式如式(1)所示:
QC=α·DVC+β·DDC
(1)
其中,α、β為權重,且α+β=1,α和β的值根據訪問者的信譽度Vrep和貢獻者的信譽度Drep進行設置,即如式(2)所示:
α∶β=Vrep∶Drep
(2)
通過調節α和β,可以動態地實現對數據精確、實時的隱私保護[10]。
根據α+β=1和式(2),可以得到:
(3)
設訪問者可信度DVC是Vrep和訪問者對應的角色屬性權限度Vper的函數,表示為函數f(Vrep,Vper)。Vrep和Vper是服從0~1之間正態分布的隨機變量,選用二維Gauss函數作為相應的函數,DVC的計算方式如式(4)所示:
DVC=f(Vrep,Vper)=
(4)
設數據貢獻者可信度DDC是Drep和對應客體資源所設置的數據隱私度Dpri的函數,表示為函數g(Drep,Dpri)。對式(4)進行調整,得到DDC的計算如式(5)所示:
DDC=g(Drep,Dpri)=
(5)
結合式(1)~式(5),可以得出查詢安全可信度QC的計算方式如式(6)所示:
(6)
然后,設置QC與隱私預算參數ε的一一映射關系。
由式(6)計算出QC的最大值QCmax和最小值QCmin,均等分可信等級區間 [QCmin,QCmax]成n(n≥3)個等級;同樣,也均分隱私預算參數ε為n份,與可信等級相對應。
設定各個可信等級與隱私保護參數εi的對應關系,即第i個可信等級的區間表示為:
其對應的隱私保護參數為εi。由此建立了從安全可信度值區間到隱私參數值區間的映射關系,該映射為一對一的。于是,可通過查詢該映射關系,實現隱私參數的細粒化設置。值得注意的是,若QC的值區間固定,同時全體數據訪問者的ε參數的取值均來自同一值區間,則優劣者之間的差異程度無法實現,難以觀測得到優者越優、劣者越劣的系統增益。因此,引入ε值估計法,通過置信區間和置信水平的設置來表達真實值在間隔估計中準確性的提升。
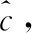

(7)
定義4(誤差尺度) 誤差尺度w表示為噪聲數據所被允許的誤差比例,且w∈(0,1)。
定義5(輸出概率) 數據貢獻者在共享數據時,設置數據的誤差尺度為w,且被訪問的概率為p,且p∈(0,1),即數據以w誤差尺度的輸出概率為p。
定義6(隱私保護級別) 假設以誤差尺度w為置信區間的大小,以輸出概率p為置信水平,則隱私保護級別P可用式(8)進行定義:

(8)
繼而將式(7)代入式(8),可以得到式(9):

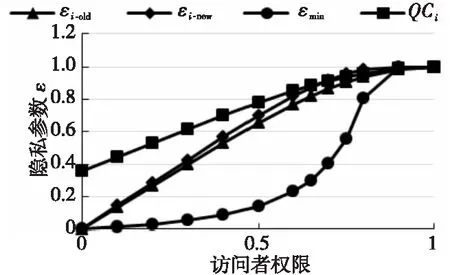
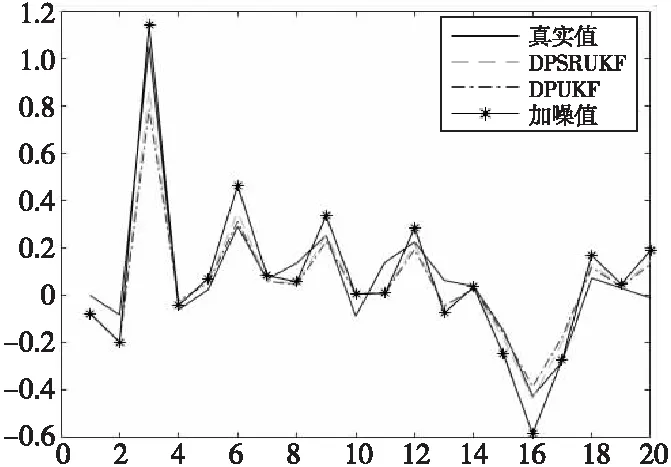
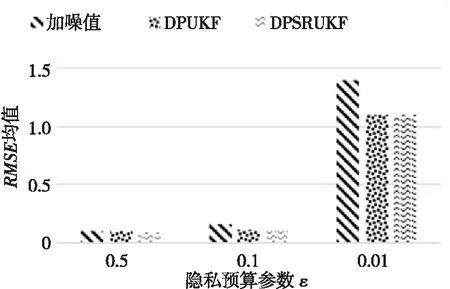
P[(1-w)·c F(wc)-F(-wc)= (9) 其中,F(·)為累計分布函數,b=Δf/ε。通過式(9)可看出,隨著真實值c的增長,ε值就越小,噪聲越大,可用性越小,隱私保護越強。 當增強數據的隱私保護時,其可用性就會被降低,所以需要在這兩者之間進行折衷。為此,本文優先考慮可用性,采用ε區間取值方法,由式(9)可知,為了取得越小的ε值,則要求誤差尺度w盡可能地大。這與可用性優先所要求的誤差尺度w盡量小是不吻合的。為此,w可采用1與數據訪問者對應角色的權限最小值之差,即wmax=1-Vpermin,Vpermin表示數據訪問者所在機構角色權限的最小值,這樣數據訪問者的權限更大、級別更高時,則得到的數據更精確。 與此同時,為了最小化ε的值,需等價最小化輸出概率p。此時的p值可以表示為數據貢獻者的信譽度,于是有pmin=Drepmin。由于0 Table 1 Query trust level and privacy budget parameter comparison 由此可見,與基準算法相比,改進的隱私參數設置算法,在一定程度上縮小了隱私預算參數的取值區間,這就使得數據訪問者的信譽度越高時,獲得的數據添加的噪聲就越小,數據的可用性就越高;算法中將數據的信任等級、查詢安全可信度與隱私預算一一對應,使得數據貢獻者與數據訪問者的交易更方便。本文提出的RBPPA如算法1所示。 算法1RBPPA 輸入:Vrep,Vper,f(V)=(Vrep,Vper),Drep,Dpri,g(D)=(Drep,Dpri),n,w,p。 輸出:εi。 步驟1初始化Vrep,Vper,Drep,Dpri; 步驟2 foreach access request: 步驟4f(Vrep,Vper)=exp 步驟 5DVC=f(Vrep,Vper); 步驟6foreach objects: 步驟8DDC=g(Drep,Dpri); 步驟9endfor 步驟10QC=α·DVC+β·DDC; 步驟11endfor 步驟14endfor 步驟15QCmax= 1;QCmin= 0; 步驟16forQCin [QCmin,QCmax]: 步驟17把[QCmin,QCmax]平分為n等份; 步驟18對照表1,查出QCi對應的εi; 步驟19endfor 步驟20returnεi. 首先,對提出的與QC區間進行一一映射的ε最小值區間的確定方法進行實驗驗證與分析,設式(6)QC映射的結果表示為εi-old,設將系統中各參數的最大、最小值代入式(6)后確定與QC映射的結果表示為εi-new,將其與映射關系中QCi進行對比。從圖3右向左看,可以看出,當訪問者權限變小時,εi-old與εi-new之間的差值在變大。實驗表明,給定的εmin的值在隨著訪問權限的減少而減少,并且εmin越來越接近0。而且,經過重新劃分后映射出的ε值相對于原值稍有提升,提高了數據的可用性。 Figure 3 Relation of data visitor permission values and privacy parameters圖3 訪問者權限值與隱私參數的關系 圖4給出了εi-new與輸出概率p和誤差尺度w百分比的關系。圖4表明,當訪問者有較高的權限時,其有較大的輸出概率,它的誤差尺度就會較小,其εi-new較大,則有較高的數據可用性。該結論與實際需求一致。由此驗證了p和w的引入是合理的。 Figure 4 Relation of privacy budget, output probability and error scale圖4 隱私預算與輸出概率和誤差尺度的關系 在第2節差分隱私的隱私參數設置算法設計中,從保護數據貢獻者的角度出發,通過將細化映射預算分配所獲得的隱私預算參數與差分隱私技術結合,實現對數據的擾動處理。但是,對于數據訪問者,其關心的重點則是數據的可用性,包括數據的精確程度、來源的真實程度等。為了更好地保障訪問者的數據可用性需求,本文在文獻[12]所提出的無味卡爾曼濾波DPUKF(Differential Privacy algorithm based on Unscented Kalman Filter)提升數據精度的辦法之上進行改進,引入平方根形式的矩陣分解方法[13],提出基于平方根無味卡爾曼濾波的差分隱私數據優化算法DPSRUKF,縮小計算的誤差[14,15],從而實現數據精度的再提高。 DPSRUKF算法流程框架如圖5所示。 Figure 5 Framework of DPSRUKF algorithm圖5 DPSRUKF算法流程框架 依照圖5,DPSRUKF算法流程表述如下: (1)讀取關于數據訪問者的訪問權限等有關的數據隱私保護參數; (2)讀取被訪問數據對應的隱私預算,根據隱私預算值,對數據添加Laplace噪聲; (3)將含有噪聲的數據傳給平方根無味卡爾曼濾波處理器進行處理,實現優化處理; (4)如果(3)的結果是正優化,則完成數據隱私保護和優化,并遞交給上一層客體訪問點;否則,如果是負優化,則轉向(2),對數據重新進行優化處理。 算法2DPSRUKF算法 輸入:原始數據向量集{xi(0)}(i=1,2,…,n),ε。 輸出:加噪并優化后的數據向量集{ri(k)}。 步驟2 whileture 步驟3 foreach data in {xi(k)}: 步驟4x′i(k)=xi(k)+Lap(λ); 步驟6Xi,k|k-1=Fi(k-1,ξi,k-1); 步驟18Si(k)=cholupdate{Si(k,k-1), Gi(k)Si,yy-1}; 步驟20k=k+1; 步驟21if{ri(k)}比{xi(k)}精度更高: 步驟22return{ri(k)}; 步驟23 endif 步驟24 endfor 步驟25 endwhile 定理1DPSRUKF算法是滿足ε-差分隱私的。 證明函數f:D→Rn,若 f(D)=(x1,x2,…,xn)T f(D′)=(x′1,x′2,…,x′n)T= (x1+Δx1,x2+Δx2,…,xn+Δxn)T 則有: 設xi=0,f(D)=(0,0,…,0)T,f(D′)=(Δx1,Δx2,…,Δxn)T,O=(y1,y2,…,yn)T,有 由上面的推導可知,對每個xi查詢滿足了差分隱私保護,隱私預算為εk=ε/M,由于差分隱私滿足組合性質,所以 DPSRUKF算法是滿足ε-差分隱私的。 □ 實驗測試一組普通非線性函數,隱私預算參數取0.5。設置對比實驗,分別對比真實數據、加噪值(對真實數據按差分隱私要求添加拉普拉斯噪聲之后的稱為“加噪值”)、無味卡爾曼濾波DPUKF算法輸出數據和DPSRUKF算法輸出數據,結果如圖6所示。 Figure 6 Comparison of estimated deviations圖6 估計偏差對比 表2表明,DPSRUKF算法優化了DPUKF算法的數值,提高了加噪數據的可用性。 進一步,隱私預算ε取0.1,0.01,在不同ε下比較產生的誤差值平均值,結果如圖7所示。通過圖7可以看出,隱私預算的值與誤差值負相關,隱私預算的值越小,誤差越大,即數據的可用性越小。因此,DPSRUKF算法能夠有效提升隱私數據的可用性。 Table 2 Root mean square error RMSE Figure 7 Comparison of error values under different ε圖7 不同ε下的誤差值對比 本文提出了一種基于信譽度、數據隱私權限和數據訪問者權限相互關聯的差分隱私的隱私參數設置算法和一個加噪數據優化的算法。隱私參數設置是建立在隱私參數查詢安全可信度一一映射的基礎上,設計了隱私參數的細粒度設置方法,實現用戶對隱私更自主的保護,提高了差分隱私技術的靈活性和有效性;針對加噪數據可用性降低的問題,采用了平方根無味卡爾曼濾波算法進行處理,使數據的可用性得到提高。下一步的工作將完善去中心化下共享機制的隱私保護技術,助力構建更加公平、公開、高效安全的網絡共享共治平臺。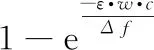
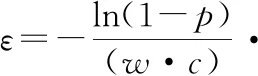
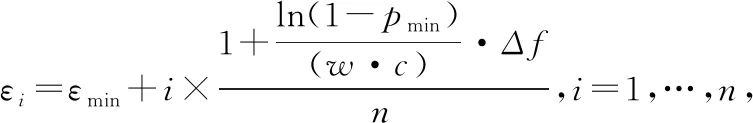

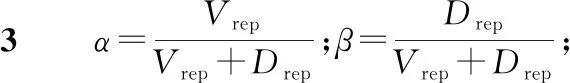
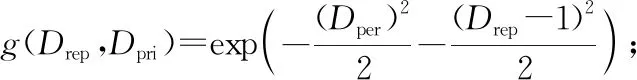
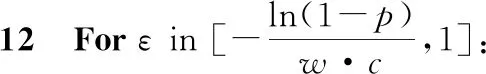
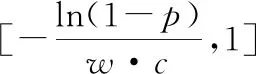
2.3 實驗分析
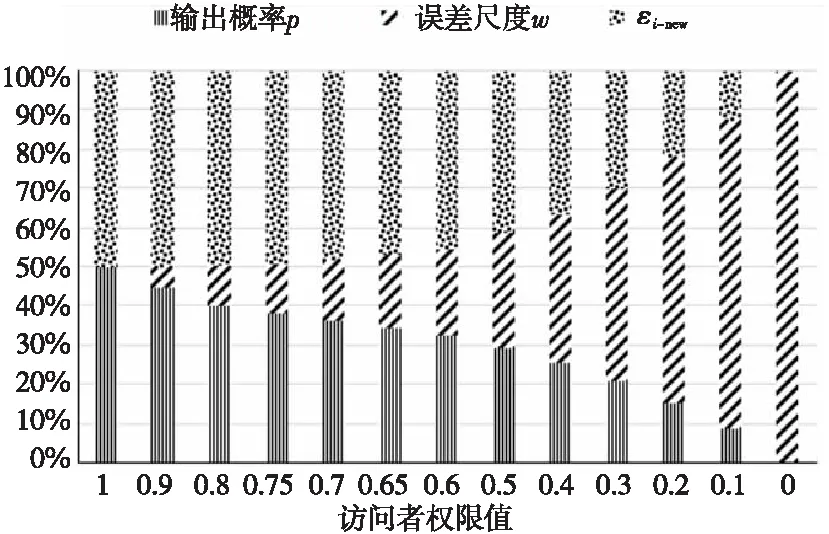
3 加噪數據優化算法
3.1 DPSRUKF算法流程
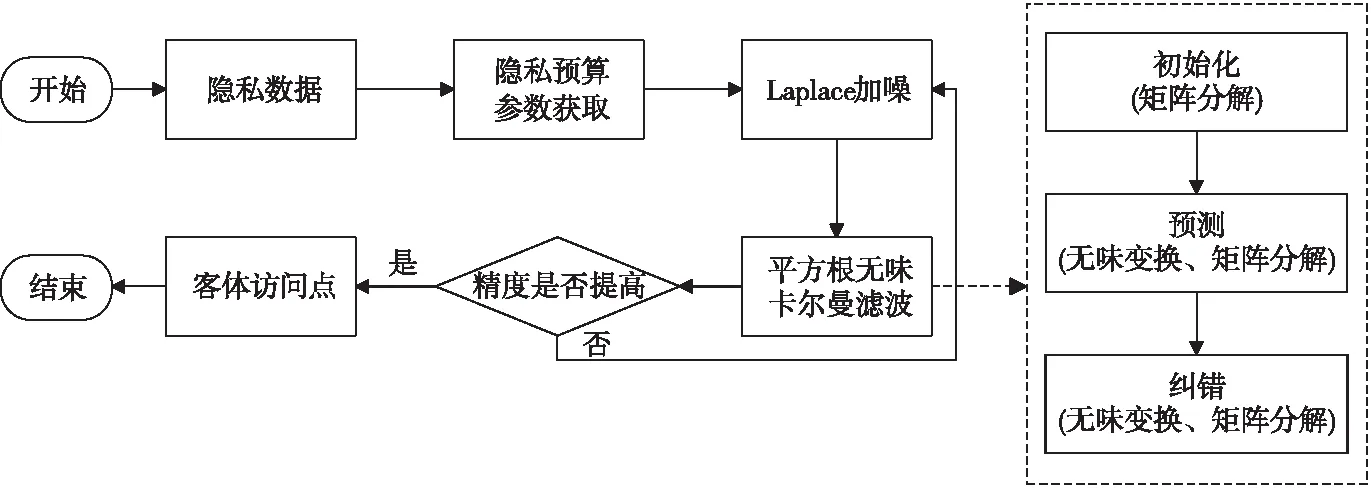
3.2 算法表述
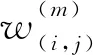
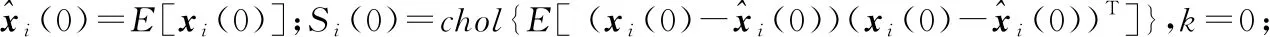
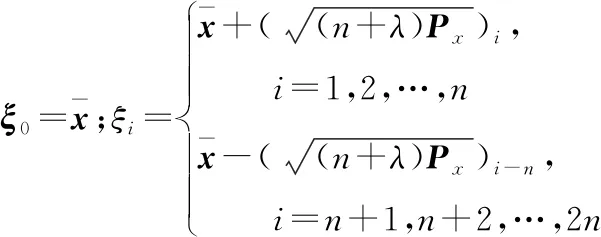
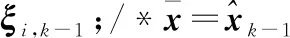
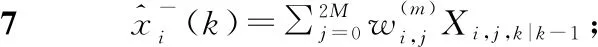
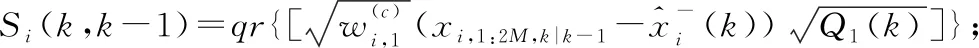
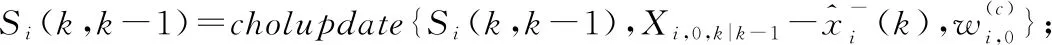
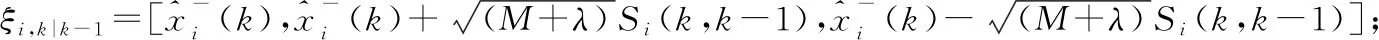
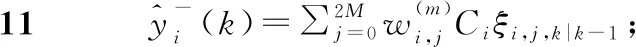
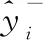
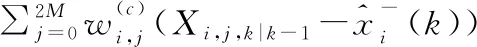
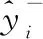
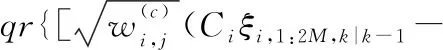
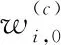
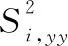
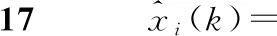
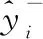
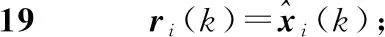
3.3 分析與實驗

4 結束語

