倍的認識：用“幾個幾”的視角看世界

周曉林

【摘 要】“倍的認識”是學生構建乘法結構的關鍵課，具有重要的研究意義和研究價值。本文基于關鍵問題進行教材研讀，通過教材脈絡的梳理和分析比較，確定了以“倍的認識”構建乘法結構的關鍵問題是“如何用‘幾個幾的視角去構建兩個量之間的倍數關系”，并設計了相應的學生學習活動對關鍵問題進行破解，構建課堂教學的基本框架。

【關鍵詞】倍的認識 幾個幾 關鍵問題

“倍的認識”作為一節典型課，小學數學教師都很熟悉。這節課之所以重要，是因為它是學生構建乘法結構的關鍵節點和關鍵課。在學習“倍”之前，學生頭腦中建構的是加法結構，是數量的合并與分解、多與少的比較，未曾學習兩個量之間的比例關系。學生在二年級學習“乘法初步認識”時，所學內容本質上還是數量的合并，是同一類量的“等合”，也就是“等量組的聚”，并沒有涉及兩個量之間的比例關系的研究。

對兩個量或多個量之間的比例關系問題的真正理解需要在學生頭腦中建構起乘法結構，而“倍”的學習正是建構乘法結構的伊始，因此“倍的認識”這節課具有非常重要的研究意義和研究價值。

一、教材研讀，理脈絡

教材首先出示的是一幅主題圖（如圖1），讓學生用數學的眼光去觀察，可以看到圖中有兔子和蘿卜，再進一步，可以觀察到兔子中有不同數量的灰兔、白兔和黑兔，蘿卜中也有不同數量的白蘿卜、胡蘿卜和紅蘿卜。

根據已有的數學活動經驗，學生可以進行梳理和歸類，把兔子和蘿卜進行分門別類，記錄各自品類的數量：

蘿卜：胡蘿卜2根、紅蘿卜6根、白蘿卜10根。

兔子：小黑兔1只，小灰兔2只，小白兔3只。

從這份材料里，學生可以進行合計，計算出蘿卜和兔子的總數量，或者進行比較，計算彼此之間的數量差，這些都是學生已有的關于“加法結構”的知識經驗。

乘法結構則是一個概念體系，涉及乘法與除法，以及與之相關的倍、最大公因數、最小公倍數、運算律，甚至面積、體積、表面積、速度等概念和定律。學生已經具備了乘法和除法的相關知識，有了比較兩個量的比例關系的知識和能力基礎。教材隨之出現的學習材料（如圖2）就是在引導學生探究用“乘法結構”來構建兩個量之間的倍數關系。

“胡蘿卜有2根，紅蘿卜有3個2根，我們說紅蘿卜的根數是胡蘿卜的3倍。”教材以舉例的方式讓學生明白“3個2根”就是3倍。然后讓學生自己照樣子去描述白蘿卜和胡蘿卜的關系（如圖3）。

從上面兩份材料，我們可以看出“倍的認識”作為學生構建“乘法結構”的起始課，其知識和經驗的基礎是“幾個幾”。學生在學習“乘法的初步認識”時，已經感受到了“幾個幾”這樣的結構。

圖4是“乘法的初步認識”一課，教材中的一幅配圖，對比圖2與圖4我們可以很清楚地發現兩者的不同：“乘法的初步認識”是基于同一類東西的“等合”;“倍的認識”是兩個量之間的比例關系。我們在計算小火車上小朋友的總數和比較胡蘿卜、紅蘿卜兩者關系時，視角都是“幾個幾”。但是計算小朋友的總數時，“幾個幾”可以隨著數數方式的不同而有變化;比較胡蘿卜、紅蘿卜兩者關系時，“幾個幾”則相對固定，以胡蘿卜的數量2根為標準去度量紅蘿卜的數量，得出有幾個2根。

二、厘清脈絡，找關鍵

從前面教材脈絡的梳理和分析比較中，我們發現構建乘法結構的關鍵是用“幾個幾”的視角去對比兩個量之間的關系。因此，這節課的關鍵問題是“如何用‘幾個幾的視角去構建兩個量之間的倍數關系”。

用“幾個幾”的視角去觀察兩個量，構建兩個量之間的倍數關系，就需要找到標準量，也就是以什么量為標準去刻畫和度量另一個量，這本質上和度量物體是一致的，具有相同的結構。

有了這種度量的意識和視角，除了整數倍之外，相應的幾倍多幾和幾倍少幾都可以蘊含其中，與學生已有的度量經驗和思想方法溝通融合。

梳理相關“倍的認識”的課例，筆者發現很多教師在上課的時候，著重讓學生觀察兩個量，思考兩個量之間有怎樣的關系。當學生說出了“甲是乙的2倍”后，立刻設置學習活動，讓學生用自己的方式去表達為什么是2倍，描述2倍在哪里。例如，“畫一幅圖表示：△的個數是□的2倍。”

這樣的學習活動可以讓學生體會到兩個量之間的倍數關系，但是缺乏生長性，會局限于具體的兩個量，難以將知識遷移，難以去理解其他的各種各樣的量的關系，這也是學生出現學習困難的根源所在。

我們都知道，要建立“倍”的概念，其關鍵是讓學生體會“關系”與“標準”的意義。那么如何讓學生體會這種標準的構建呢？如何基于關鍵問題引導學生建立和體會標準呢？

三、基于關鍵，研學情

那么，基于這樣的關鍵問題，學生自主構建兩個量之間的關系時可能會出現怎樣的情況呢？我們就此展開了學生的學情研究，設計了如圖5所示的學情研究單。

胡蘿卜的根數可以直接用數2來表示，紅蘿卜的根數當然也可以用數6來表示，學習活動提出的要求是不直接用數來表示，你會怎么說紅蘿卜的根數呢？那么學生可能會出現怎樣的描述呢？我們來看學生的表現：

（1）用乘法：3×2=6，2×3=6，或1×6=6。

（2）用描述：2根分一組，2×3=6;左邊3根，右邊3根。

（3）畫圖表達：和畫的圖一樣多○○○○○○、△△△△△△。

（4）圈一圈：兩個圈一組，圈3組。

（5）加法表示：3+3=6，2+2+2=6。

（6）和胡蘿卜聯系：比胡蘿卜多4根。

（7）用倍表達：紅蘿卜的根數是胡蘿卜的3倍，胡蘿卜=1包，紅蘿卜=3包，1包=2根，2+2+2=6根。

下面是學生的兩份學習作品（如圖6和圖7）：

可以看出，上面的兩個學生都能基于“2根”的視角去看紅蘿卜的數量，圖6所示的作品是加法結構的呈現：2+4=6（根）。當然也有2+2+2=6（根）和1+1+1+1+1+1=6（根）兩種形式，凸顯了“等量組的聚”的特征。

圖7所示的作品呈現了乘法結構的特征：2個一組圈在一起，圈了3組，恰好是2×3=6;他還畫圖表示出3個一組和2個一組的不同方式來描述紅蘿卜的根數。

通過學情研究，我們發現學生能夠用加法、乘法、圈一圈、畫一畫等方式來描述紅蘿卜的根數，但是沒有凸顯基于胡蘿卜的根數去表達紅蘿卜的根數。學習活動的任務不能很好地驅動學生去自主構建兩個量之間的內在的乘法結構。

四、基于關鍵，設活動

基于關鍵問題“如何用‘幾個幾的視角去構建兩個量之間的倍數關系”和前面的學情研究，為了凸顯學生學習活動中要基于一個量去構建和另一個量之間的倍數關系，我們設計了如圖8所示的學習活動單。

學習活動采用了度量的形式，驅動學生用“□□”去度量○的個數。兩個□在這個學習活動中組成了一把尺子，一把用來度量○個數的尺子。那么，學生對于度量結果會有怎樣的表達和描述呢？我們來看看學生的作品。

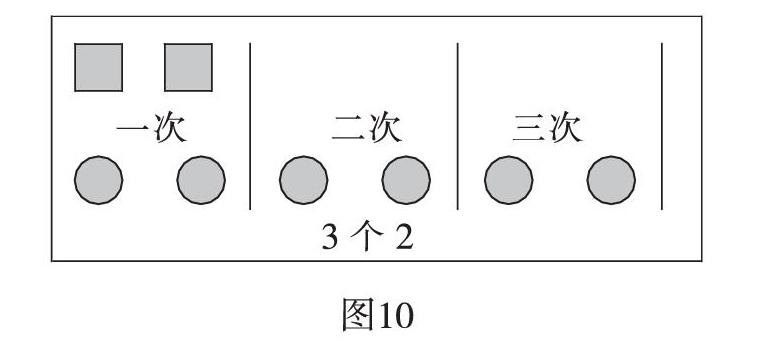
第一類作品（如圖9和圖10）：

圖9清楚地表示出從量2塊，到4塊，再到6塊的過程，用分隔線和類似線段圖的方式表示量了3次，所以就有了對應的算式：2×3=6（塊）和2+2+2=6（塊）。

圖10則有所區別，它更突出地表達了度量的次數“一次、二次、三次”，所以就會得到度量結果“3個2”。

第二類作品（如圖11和12）：

上面兩幅圖生動地再現了用2個□去度量6個○的過程，2個2個地量，量了3次，所以有這樣的3組，有2×3=6。

第三類作品（如圖13和圖14）：

和前面的有所不同，這兩幅圖用對應的方式表示○里有“3組相應的2”，把2個□和2個○一一對應去描述。

第四類作品（如圖15和圖16）：

這兩幅圖相對更為簡潔，圖15用箭頭的方式表示量了3次，所以下面的○被圈成了3組。圖16則省略了這一過程，直接用圈一圈的方式表示度量的結果。

從學生的這些作品來看，因為“度量”的任務驅動，量了3次，分了3組，有三個一一對應的量，給學生留下了深刻的印象，他們都在用自己的方式去表達和描述“3個2”，這為接下來“倍的意義”的學習做好了充分的準備。

五、梳理素材，設教學

根據基于關鍵問題的教材研讀和學生研究，在充分解讀學生學習活動成果的基礎上，我們可以設計基于關鍵問題破解的教學方案，構建課堂教學的框架。

面對學生在學習活動中展示的素材，我們在進行梳理和分析后，可以借助這些素材，組織學生分類、辨析和評價，在分析和比較中感受“你能用‘□□去‘量一量○的個數嗎”這一數學活動的價值。

（一）問題引入

1.出示：□□

看到了什么？你能用一個數來表示□的個數嗎？

2.出示：○○○○○○

看到了什么？我們不直接用數來表示○的個數，如果把“□□”看成一把尺，你能用它來“量一量”○的個數嗎？

（二）學生活動

1.出示學習活動單（見圖8）：用你自己喜歡的方式表示你的度量結果。

2.學習活動作品的分享和交流：思考他人是怎么度量的，是怎么表示度量結果的。

3.小結：這些作品度量的結果有什么共同特點？

（都表示出了○中有3個2）

（三）揭示概念

1.引出概念：通過剛才的學習活動，我們知道了□有2個，○有這樣的3組2個，我們就可以說○的個數是2個的3倍。

2.想一想，“2個的3倍”還可以怎么說？

引出：正方形的3倍;圓形是正方形的3倍。

3.你能照樣子說一說□和△的關系嗎？

□? □

△? △? △ △? △ △? △ △? △ △

引導得出：5組2個;2個的5倍，正方形的5倍，三角形是正方形的5倍。

4.概括總結：像這樣的圓形有3個2，三角形有5個2，我們就說圓形是正方形的3倍，三角形是正方形的5倍。我們一起來說一說。

引出：這就是我們今天要學習的內容——倍的認識。

（四）練一練

1.圈一圈，填一填。

第二行的個數是第一行個數的（? ? ? ）倍。

第三行的個數是第一行個數的（? ? ? ）倍。

2.把原來的2個□變成3個□。

現在圓形是正方形的（? ? ?）倍。

3.畫一畫，填一填。

在學生以“幾個幾”的視角去觀察數學現象的基礎上，引導學生用數學的語言來描述世界，用數學模型來構建2個□和6個○之間的關系，凸顯2×3的乘法結構和“3個2”的圖示形式。當學生明晰了概念，我們就可以讓學生用“倍”的結構和方式去觀察學習素材，去表達自己看到的數學世界。至于如何用算式來描述和表達兩者的關系，這就是下一節課需要研究的內容了。

總之，我們在對教材的梳理和研讀中尋找構建乘法結構的關鍵點，基于“倍”的概念的建立設計相應的學習活動，以關鍵問題為切入口引領和組織學生展開自主探索、互動交流和匯報討論，在經歷數學學習活動的過程中感受用數學的語言描述生活中的數學現象，學會用數學的眼光觀察世界和思考世界。