對數比較大小,反思解題技巧
——以2020年全國高考數學全國Ⅲ卷文科第10題為例
◎李曉梅 孔德宏 (云南師范大學數學學院,云南 昆明 650500)
一、引言
對數比較問題是高考熱點題型,一定程度上反映了學生的數學運算、直觀想象、數學抽象等核心素養[1],那么底數不同、真數也不同的對數比較大小可采用何種方法解題?本文以2020年全國高考數學全國Ⅲ卷文科第10題為例對該問題進行探究.
二、試題呈現
A.a 數值比較大小的常用方法有作差法和作商法,而對數比較大小常見問題可分為三類:(1)底數相同的對數可利用函數單調性進行比較;(2)真數相同的對數可利用圖像法進行比較;(3)底數不同、真數不同的對數引入中間變量(0,1等)進行比較.[2]在實際應用中,直接引入中間變量往往較難實現,需結合條件轉化解決.本文從學生做題情況考慮,闡述作差法、作商法、換底公式、放縮法等不同解法[3],探究底數不同、真數不同的對數比較大小的解題技巧,具體解法如下文. 由題易知:0 注:先將對數與常數作差比較,可進一步化為同底數的兩對數相減,借助對數運算性質,兩數相減后得到的值是一個可判斷正負的對數. 注:與作差比較法類似,先與常數做比較,化簡變形的過程要注意對數式與同底數對數比較大小的情況. 注:將對數的底數都換成自然數e,簡化計算過程,方便學生計算,在判斷正負的過程中穿插對數函數的單調性知識. 注:將三個數兩兩轉化為同底數的對數進行比較,便可利用函數單調性判斷大小. 注:該解法與解法4類似,本質是化為同底數的真數兩兩比較,但相較于解法4,該解法從數值本身出發,考慮真數部分值的大小,計算量明顯減少. 解法6(放縮法):若a>b>0,k>0,則有ka>kb.可根據此不等式的性質將對數式進行放縮,將三個數值均放大3倍后大小關系不變,此時3a=3log32=log38,將3a的值與最接近的整數作大小比較,即引入中間變量,有3a=log38 注:將對數a乘以k后,使得對數ka盡可能接近整數,方便計算.本質是引入整數類的中間變量,使用時需把握放縮程度,減少計算量. 從一道對數比較大小的高考選擇題的求解過程中可以看出高考題目的靈巧多變,更為學生學習以及教師教學引發一定思考,所謂“一題多解”更多反映的是解題思維和技巧的靈活多變,是對同一問題的多角度探究,是學生實踐能力和創新意識的提升. 底數不同、真數不同的對數比較大小多引入中間變量,需觀察對數式構造合適的中間變量,將對數作適當變形.本題給出了兩個對數式、一個分數,一定程度上給了學生明顯的提示,即考慮分數的作用,引入中間變量,或在變形過程中,考慮分數值指明的化簡方向.底數不同、真數不同的對數比較大小,往往與底數相同的對數以及真數相同的對數比較大小問題息息相關,并不局限于某種固定的方法,實際求解需結合條件靈活運用,要求學生熟練掌握對數運算性質和對數函數單調性的相關知識,深入理解數形結合思想方法更有助于問題的解決.教師則需注意從學生的角度考慮解題思路,培養學生解題思維與技巧,及時發現問題并給予引導,鍛煉學生解決問題的能力,發展學生核心素養,激發學生學習興趣,讓學生感悟數學的魅力.三、解法探究

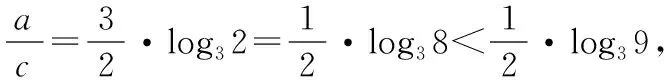

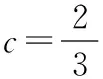
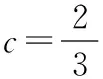
四、解題反思

