函數凸性條件“弱化”的可能性探索

◎張逸輝 潘霄 徐蓮花 王利梅 (.對外經濟貿易大學，北京 0009;.中國航天系統科學與工程研究院，北京 00048)

《數學分析》教材(文獻[2])給出了凸函數的如下代數定義:

定義1 設f為定義在區間I上的函數，若對I上任意兩點x1,x2和任意實數λ∈(0，1)總有

f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2), (*)

則稱f為I上的凸函數；反之，如果總有

f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2)，

則稱f為I上的凹函數.

若將上述兩個不等式改為嚴格不等式，則相應的函數分別稱為嚴格凸函數和嚴格凹函數.

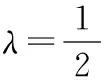
則y=f(x)是否仍為I上的凸函數.

不妨稱滿足不等式(**)的函數為中值凸函數.定義在開(閉)區間上的函數，其凸性和中值凸性有以下幾個等價關系.

定理1(文獻[3]，P101) 設y=f(x)為區間[a,b]上的連續函數，則y=f(x)為[a,b]上的凸函數的充要條件是y=f(x)為[a,b]上的中值凸函數.

證明:根據凸函數和中值凸函數的定義，只需證明充分性.

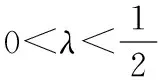
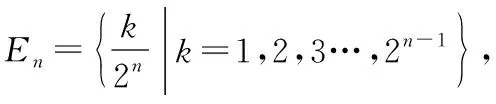
首先用數學歸納法證明：對任意正整數n，以及任意的x1,x2∈[a,b],對一切λ∈En，都有不等式(*)成立.

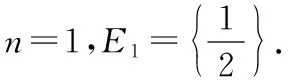
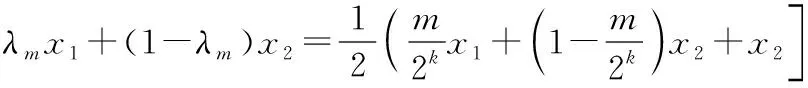
f(λmx1+(1-λm)x2)

≤λmf(x1)+(1-λm)f(x2)，

即當n=k+1時，不等式(*)對λ∈Ek+1成立.

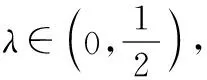
因為f(x)在[a,b]上連續，所以對任意的x1,x2∈[a,b]，有

=λf(x1)+(1-λ)f(x2).

綜上，f(x)為[a,b]上的凸函數.證畢.

定理2 區間(a,b)上的有界中值凸函數處處連續.

定理2的證明見[文獻1，P288].

定理3 區間(a,b)上的可測中值凸函數處處連續.

定理3的證明見[文獻4,P122].

注:由定理1、定理2和定理3可知，若f(x)為開區間(a,b)上的有界或可測函數，則f(x)為凸函數的充要條件是其為中值凸函數.

通過考察下例，我們可以看到定義在離散點集上的中值凸函數，即使有界，也不一定為凸函數.

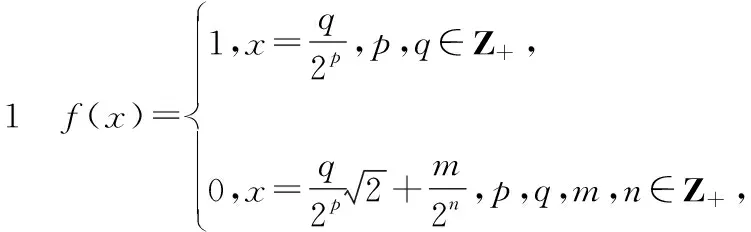
其中Z+代表正整數集.

若取x1,x2均為第一類(或第二類)的x，則顯然有

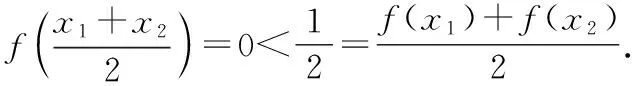
這個反例的構造，靈感源于狄利克雷函數.同樣地，反例的圖像也不能畫出.在這里，高等數學的抽象性得以體現.