水驅砂巖油藏在不同水質下的滲透率時變特征

王建忠，宋憲坤，付穎超，孫蓮婷，徐進杰

[中國石油大學(華東) 石油工程學院，山東 青島 266580]

砂巖作為多孔介質是一種天然的過濾材料。在1856年,法國工程師達西利用填滿砂子的管柱過濾城市用水發現了著名的達西定律。根據石油行業油田水質標準(SY/T 5329—2012)，將油田注入水分為5個水質等級，不同水質的注入水因污染物種類、含量和粒徑的不同，對地層的堵塞規律、傷害程度以及水驅開發效果的影響也不盡相同。這種傷害不是因為“五敏”，也不是“壓敏”，而是因為水質問題引起的，本文將這種原因稱之為滲透率水質敏感性。近些年，國內學者們的最新研究闡明了水質對提高注水開發效果的重要性[1-2]。李明忠等給出了注入水中各污染物引起表皮系數變化的具體計算方法[3]；Wojtanowicz A K、張光明和李軍等不少學者圍繞著注入水中污染物含量對地層滲透率的傷害規律做了大量研究[4-11]；Rochon J，Basan P B和Zhang N S等學者建立了簡單分析方程，預測注入水中懸浮固體對地層傷害以及影響水驅開發效果的程度[12-16]。Amanat Ali Bhatti等綜合利用水動力學及電測法對儲層滲透率進行預測[17]，Xia Dongling從沉積、成巖的角度，提出了表征儲層滲透率的方法[18]。學者們的研究意在闡明水質對注水開發效果的影響，但是對水質造成儲層滲透率傷害的規律缺乏定量描述，這在一定程度上制約著油田長期注水的水質決策。在前人研究的基礎上，本文給出注入水對地層滲透率的傷害規律的數學描述和理論推導，在一定程度上為油田長期注水的水質決策提供指導。

1 注水對砂巖油藏滲透率的傷害

油田注水過程中，常見的引起注水系統堵塞的主要因素如表1所示。實際上，地層中的孔喉對注入水中的污染物起到了一個過濾作用，我們把它稱為砂巖的過濾效應。注水開發油田進入高含水開發期后，優勢通道的形成是不可避免的問題。油田經過長期注水開發，大部分井區己進入高含水期，大量注入水沿注采優勢通道突進，造成許多區塊注入水低效甚至無效循環，大大降低了油田開發效果和經濟效益。優勢通道的形成造成了地層平均滲透率變大的假象，而實際含油區附近的地層卻已被注入水中的污染物堵塞。因此需在對識別出的優勢通道采取有針對性的封堵措施后，結合注水水質標準，選擇合適的注入水，提高水驅開發效果。

對于高含水期砂巖油藏，特別是長期注入水質不達標的水，會造成地層孔隙被堵塞，嚴重傷害地層滲透率。一方面，注入水中的污染物會在井壁或注水層端面形成濾餅；另一方面，水中的污染物會在地層孔隙內沉淀或被吸附導致孔隙變小，注入水流速越大，污染物會就會進入離注水井更遠的地層。洗井只能解決井筒表層的堵塞問題；酸化以及壓裂方式只能解決井筒附近地層的堵塞問題，而且酸化或壓裂后，注水會堵塞離井更遠的地層。

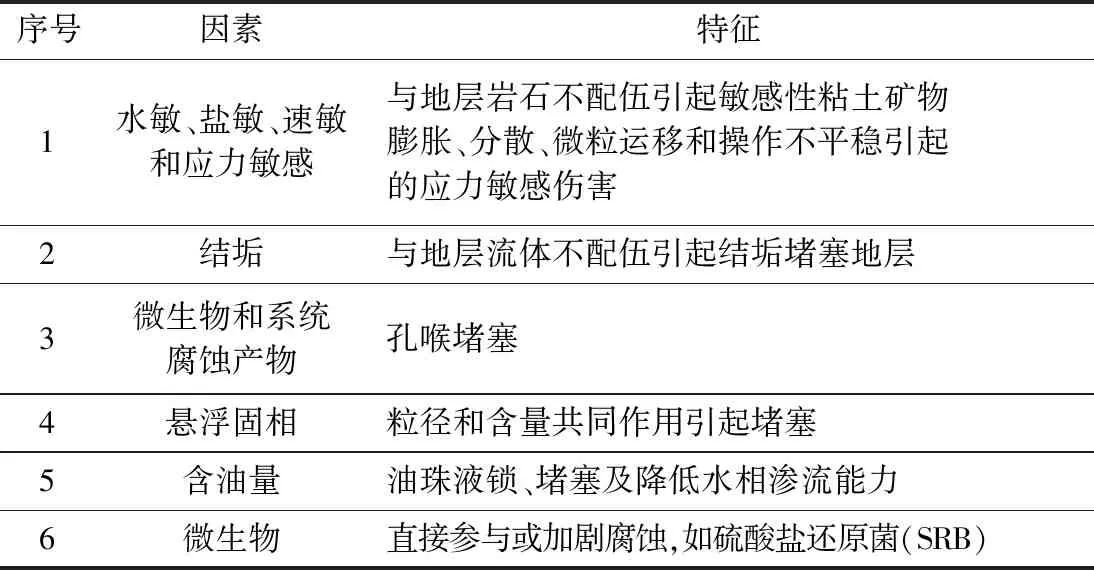
表1 引起注水系統堵塞的主要因素Table 1 Main factors causing blockage in water injection systems

2 滲透率衰減規律及表征方法

因為受不同注入水水質的長期影響，地層滲透率逐漸下降，本文把這種現象定義為地層滲透率的水質敏感性。在注入水水質標準基礎上，為深入研究地層滲透率的水質敏感性，按照注入水水質標準中5種注入層平均空氣滲透率從小到大的順序，把對應不同控制指標下的不同注入水水質依次命名為Ⅰ級水質、Ⅱ級水質、Ⅲ級水質、Ⅳ級水質和Ⅴ級水質(表2)。在表2中，僅列出了兩項主要影響水驅開發效果的水質控制指標，即懸浮固體含量與含油量。

根據理論研究結果和實驗室的實際條件，通過對大量巖心進行室內地層傷害實驗，研究5種注入水水質對不同地層滲透率注入能力的影響，得到不同地層滲透率在不同水質下的注入能力差異，即地層滲透率下降情況。進一步分析在確定注入水水質的情況下，不同地層滲透率隨無因次注入量增加而衰減的現象。實驗條件如下。

1) 實驗溫度為70 ℃。

2) 實驗水樣為注入水水質標準下以懸浮物含量及含油量為主要控制指標配置的5種水樣。

3) 儲層物性以滲透率為主，標準巖心滲透率劃分標準為：(1 500～2 000)×10-3，(500～1 500)×10-3，(50～500)×10-3，(10～50)×10-3和(1～10)×10-3μm2，在實驗過程中需在不同巖心滲透率范圍內挑選大量的巖心進行實驗。

4) 實驗中所用巖心有天然巖心和人造巖心，人造巖心膠結程度較好，無水敏性。實驗前經溶劑驅替、蒸餾水高速沖刷，避免了加工中引入的微粒物質對實驗結果的影響。天然巖心取自目標油區。

5) 鑒于水質變化相對較快，實驗過程中采用圖1所示的并聯實驗方案。

實驗流程如下。

1) 將巖樣洗油、風干、烘干后，測空氣滲透率，飽和地層水后測孔隙度。

表2 SY/T 5329—2012 注入水水質標準Table 2 SY/T 5329-2012 recommended standard for injection water quality

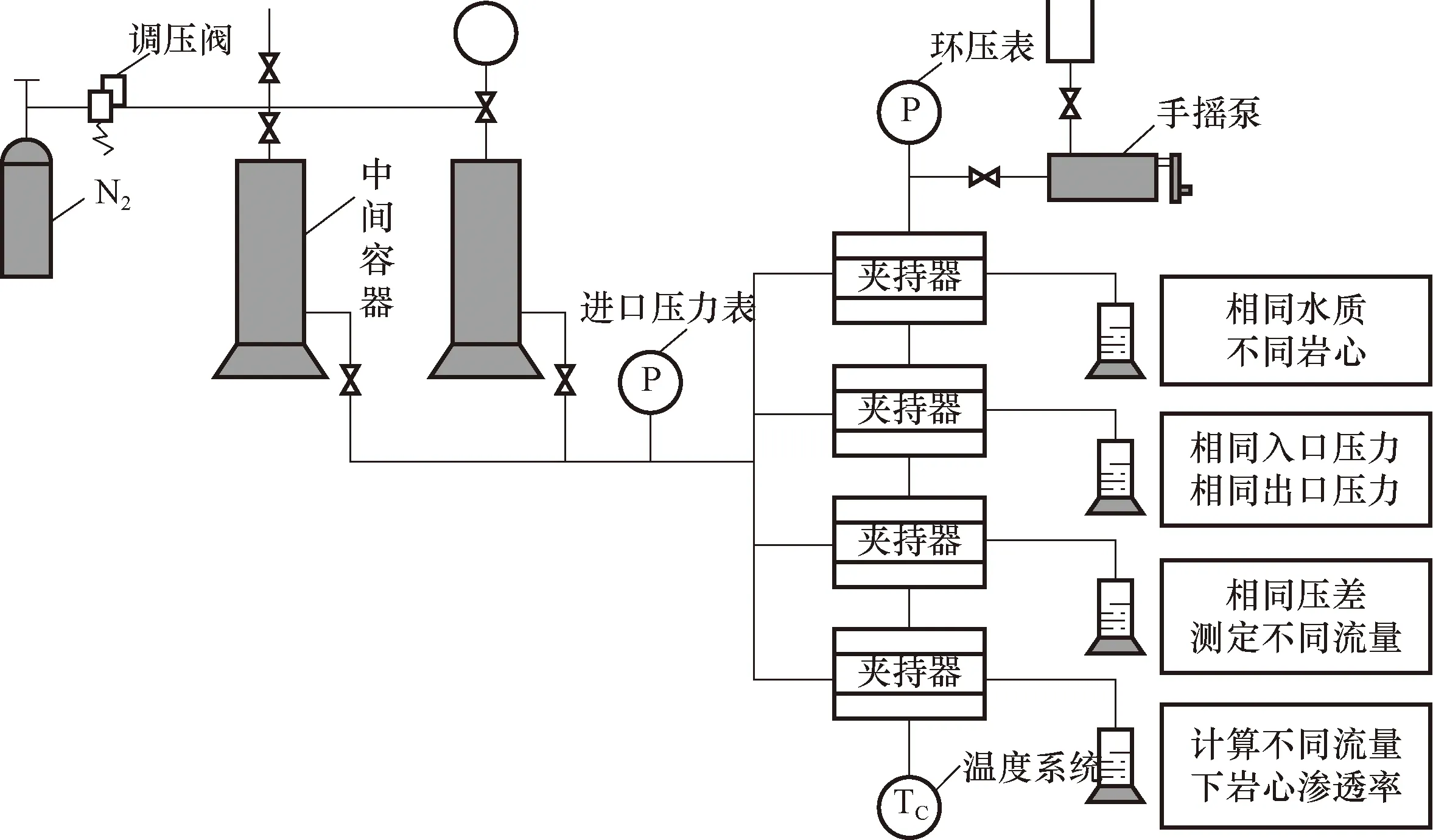
圖1 水質影響研究實驗平臺Fig.1 Experimental platform for water quality impact assessment

2) 借助地層傷害實驗設備，通過恒溫箱模擬地層溫度70 ℃，配置Ⅰ級水質，將飽和好地層水的巖心置于巖心流動裝置中，將圍壓緩慢加至2.0 MPa。實驗過程中始終保持圍壓大于上游壓力1.5～2.0 MPa，以此消除圍壓對實驗結果的影響。

3) 在恒定流速下，讓注入水大量的流過巖心，測定其滲透率隨流量增加的變化情況。控制注入水流速在臨界流速以下，并計算無因次注入量，在無因次注入量分別為5,10,20,50,100,150 和200 孔隙體積倍數(PV)時測量各巖心的滲透率，此時的滲透率K與巖心初始時的滲透率K0之比就是滲透率保留率。

其余4類水質依次用這種方法測量無因次注入量和滲透率保留率的對應數值，以此來研究滲透率保留率隨無因次注入量的變化規律，進而從定量的角度分析水質對儲層滲流物性的影響。

以Ⅰ級注入水水質條件下，滲透率為213.91 × 10-3μm2的巖心為例，根據表3中蓋巖心滲透率保留率的變化數據，經指數擬合后如圖2所示。

上圖可以看到相關性系數接近1，初步認為巖心滲透率保留率(K/K0)與無因次注入量(Qi)之間具有指數關系。在此基礎上對所有實驗數據指數擬合，如圖3所示，相關性系數均接近1，可看出在Ⅰ級水質下巖心滲透率保留率K/K0與無因次注入量Qi呈較好的指數關系。

其余4類水質依次用這種方法測量無因次注入量和滲透率保留率，并對所有實驗數據進行指數擬合。擬合結果如圖4至圖7所示，相關性系數同樣均接近1，均呈較好的指數關系。

隨無因次注入量增加，巖心滲透率不斷降低，低滲巖心比高滲巖心變化更加顯著。從開發角度考慮，因5種注入水水質的懸浮固體含量與含油量不同，故實驗巖心滲透率降低是懸浮固體含量與含油量共同作用的結果。同一種注入水水質對不同巖心滲透率區間的傷害程度不同，5種水質對同一巖心滲透率區間的傷害程度也不同，可看出地層滲透率衰減程度與地層綜合物性、注入水中懸浮固體含量與含油量有關。

在確定注入水水質情況下，隨著累積注入孔隙體積倍數的增加，巖心滲透率不斷衰減，衰減速度逐漸減慢。對注水開發的油田來說，只要注水就會增加無因次注入量，注入水中的污染物會堵塞巖心，導致巖心滲透率大幅下降。

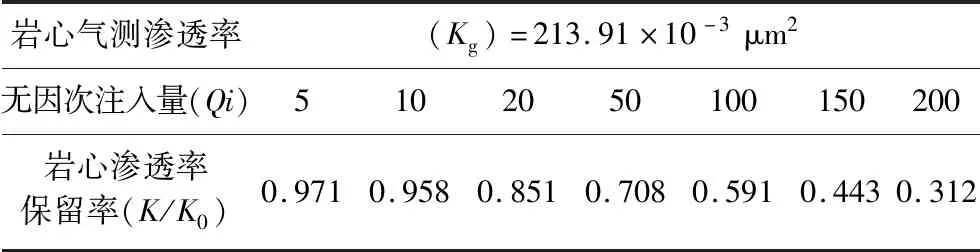
表3 Ⅰ級注入水水質條件下巖心滲透率保留率變化數據Table 3 Permeability retention rate under Class Ⅰ injection water quality

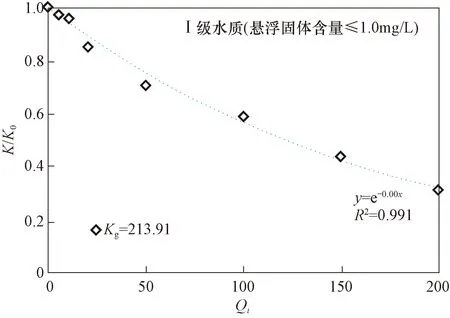
圖2 Ⅰ級注入水水質條件下巖心滲透率保留率變化擬合曲線Fig.2 Fitting curve of permeability retention rate under Class I injection water quality

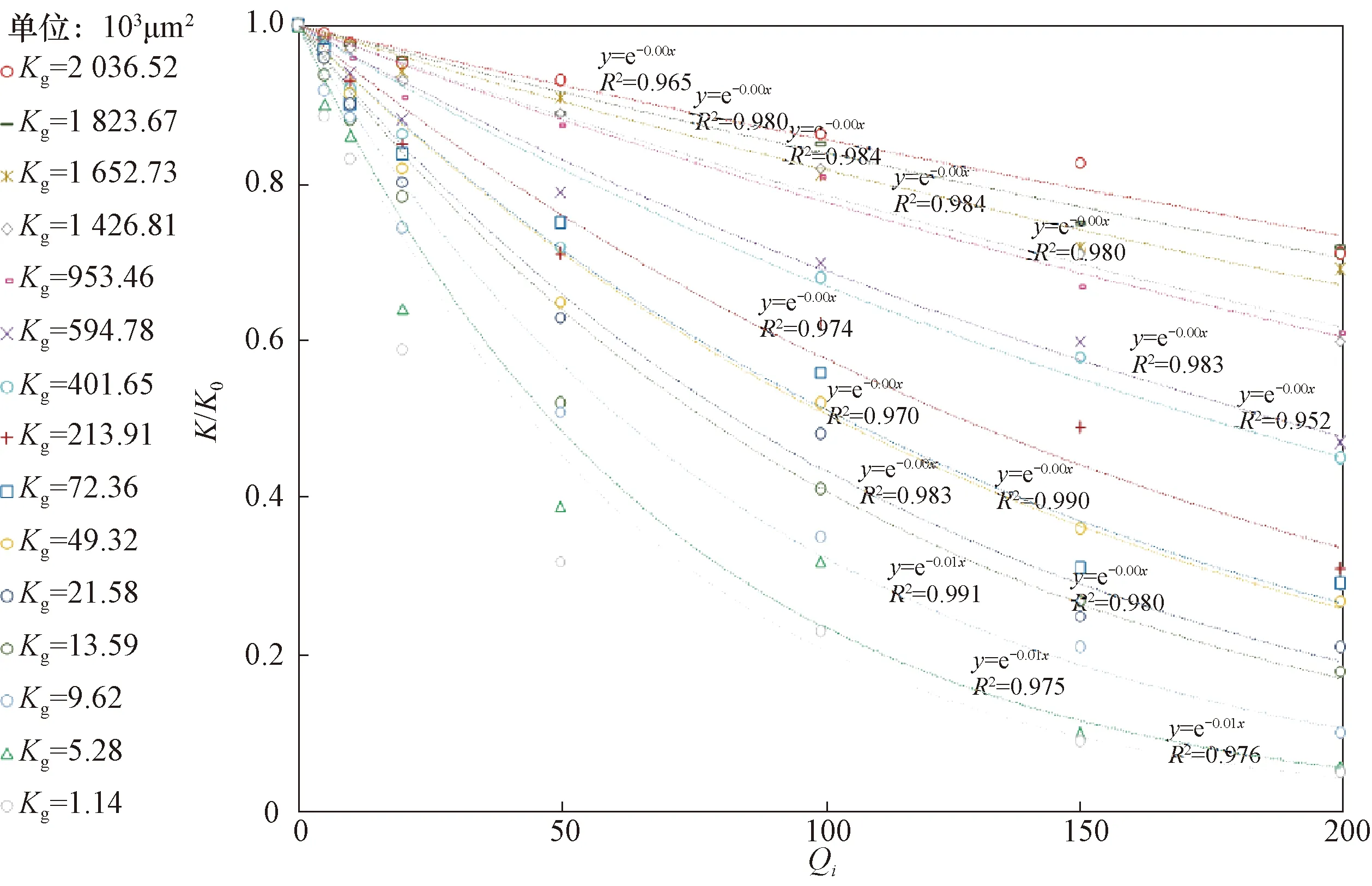
圖3 在Ⅰ級注入水水質條件下不同巖心滲透率保留率隨無因次注入量變化關系擬合曲線Fig.3 Fitting curves of permeability retention rates changing with dimensionless injection rates for different cores under Class I injection water quality

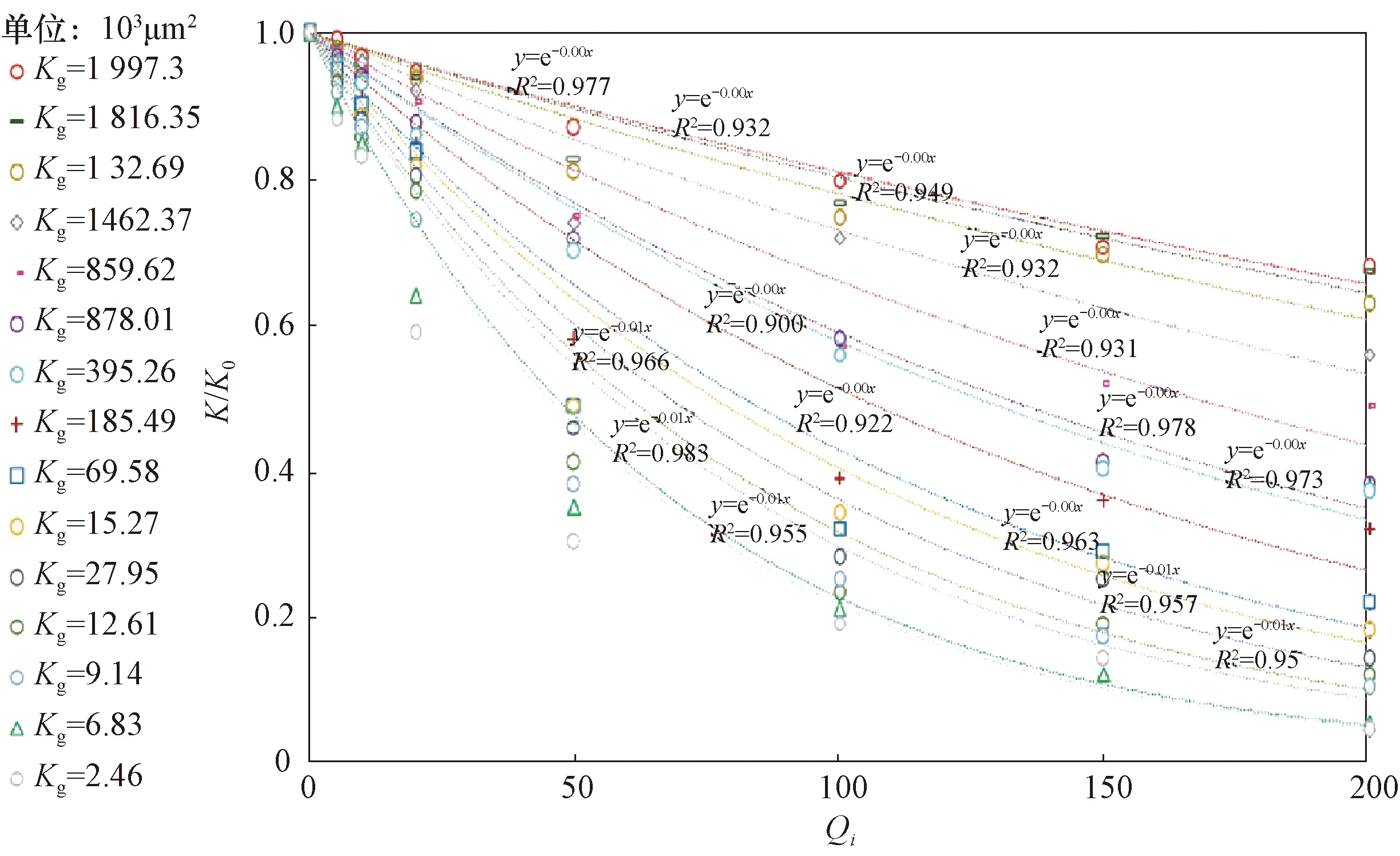
圖4 在Ⅱ級注入水水質條件下不同巖心滲透率保留率隨無因次注入量變化關系擬合曲線Fig.4 Fitting curves of permeability retention rate changing with dimensionless injection rate for different cores under Class Ⅱ injection water quality

3 滲透率水質敏感性

將圖3中各擬合公式指數中無因次注入量的倍數用θ表示，歸納得到規律公式如下：

K/K0=e-θQi

(1)

式中,θ為地層滲透率的水質敏感系數，其物理意義是在確定注水水質下，注入層單位滲透率隨無因次注入量的變化速率，10-3；K為當前地層滲透率，10-3μm2；K0為水驅開發前地層滲透率，10-3μm2；Qi為無因次注入量，即注入水的孔隙體積倍數。

根據θ的定義，可用如下公式表示：

(2)

對公式(1)分離變量積分可得：

lnK=-θQi

(3)

在水驅開發前，即Qi=Qi0=0時，K=K0，則有：

lnK0=-θQi0

(4)

由公式(3)與公式(4)相減變形可得：

K/K0=e-θQi

(5)

經理論推導得到的公式(5)與大量實驗數據擬合出的規律公式一致，說明理論充分驗證了實驗規律的正確性。將公式(5)變形可得：

K=K0e-θQi

(6)

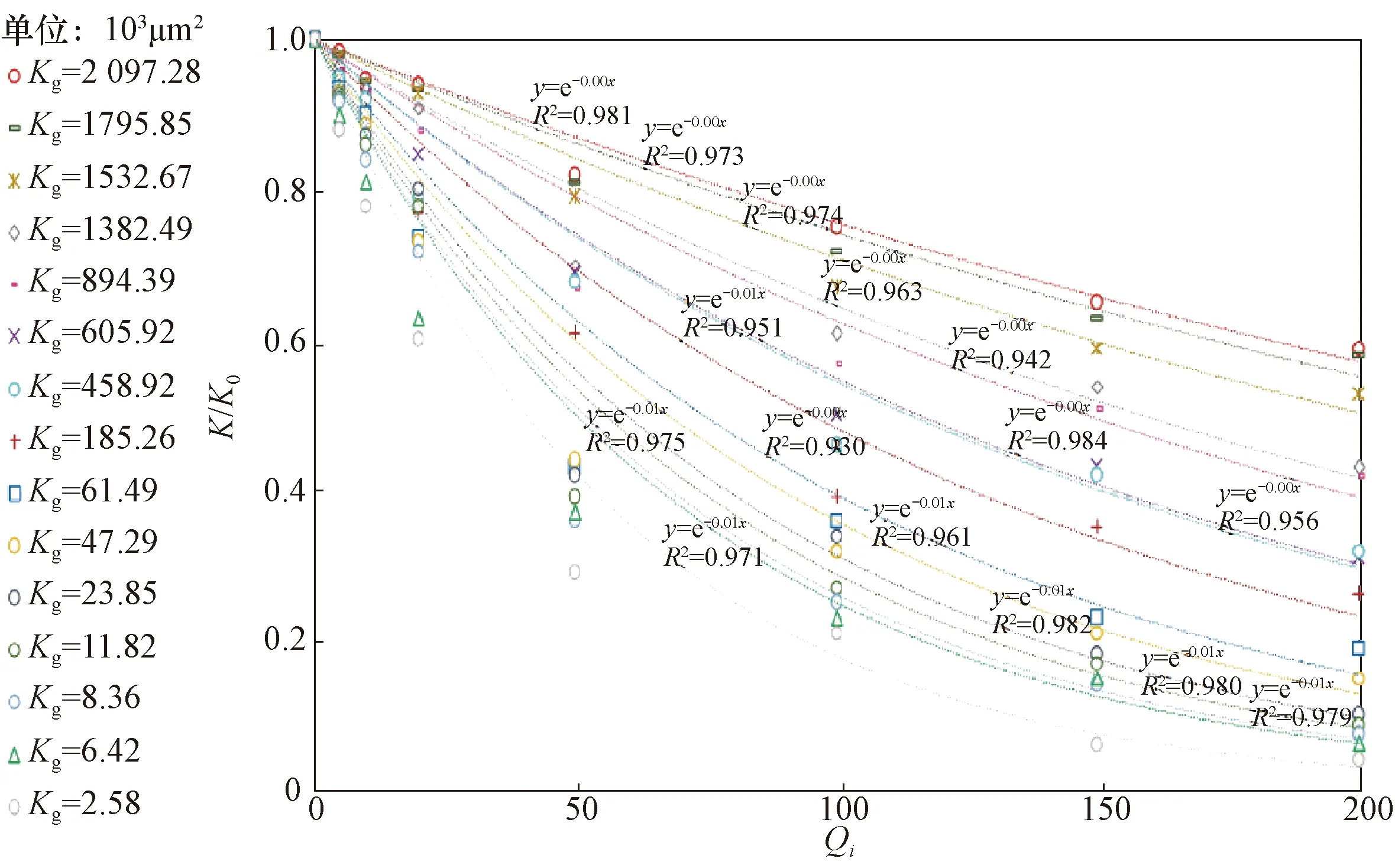
圖5 在Ⅲ級注入水水質條件下不同巖心滲透率保留率隨無因次注入量變化關系擬合曲線Fig.5 Fitting curves of permeability retention rate changing with dimensionless injection rates for different cores under Class Ⅲ injection water quality

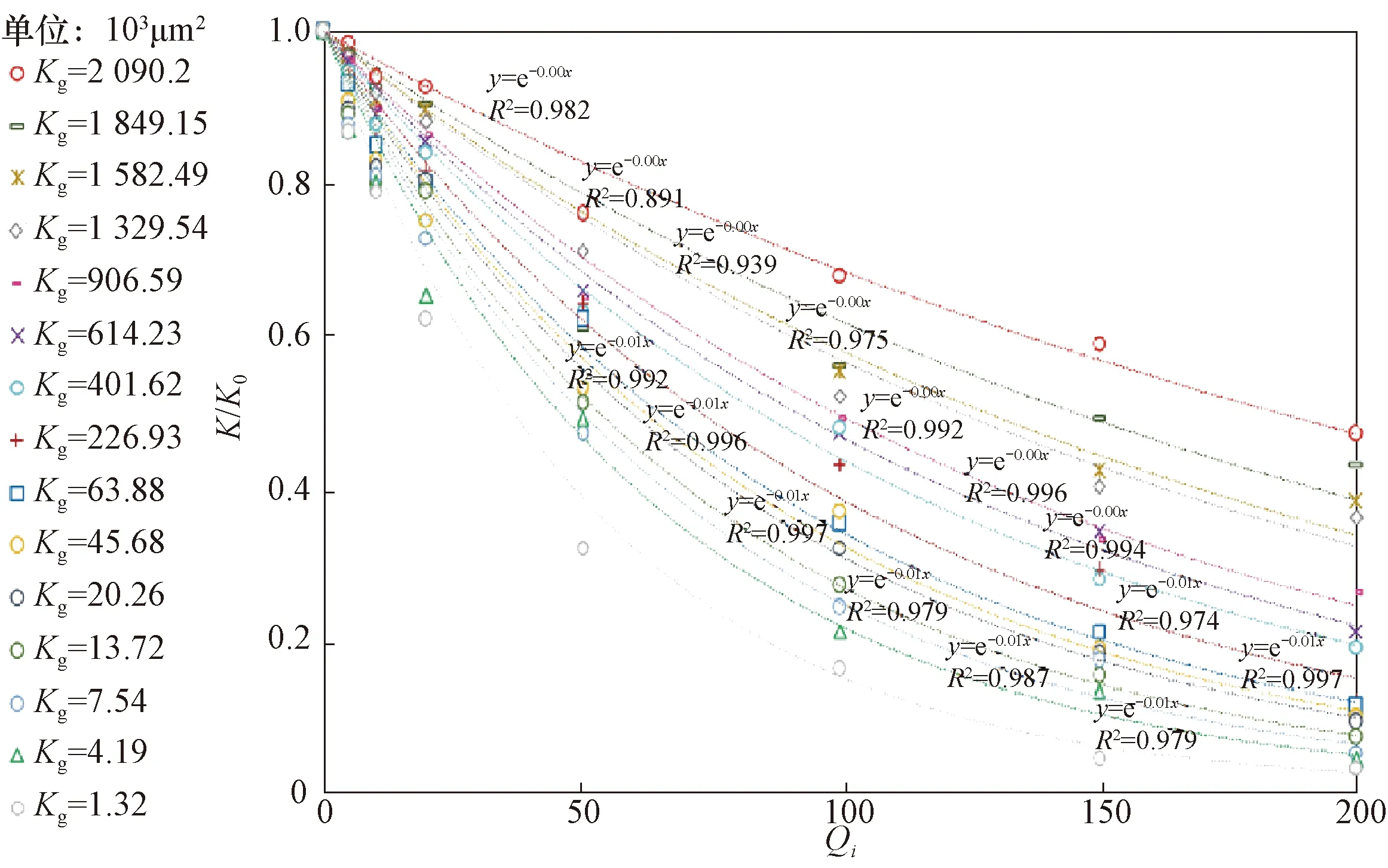
圖6 在Ⅳ級注入水水質條件下不同巖心滲透率保留率隨無因次注入量變化關系擬合曲線Fig.6 Fitting curves of permeability retention rate changing with dimensionless injection rates for different cores under Class Ⅳ injection water quality

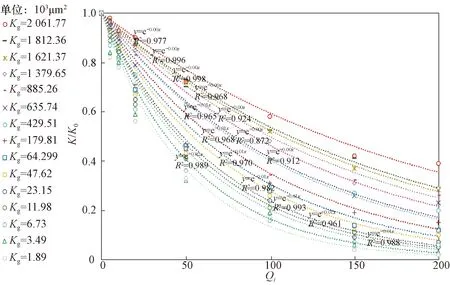
圖7 在Ⅴ級注入水水質條件下不同巖心滲透率保留率隨無因次注入量變化關系擬合曲線Fig.7 Fitting curves of permeability retention rate changing with dimensionless injection rate for different cores under Class V injection water quality

通過公式(6)，可定量計算或預測在確定注入水水質條件下，目的地層經歷一定注水歷史后，其滲透率的變化規律。由上可看出，高含水期老油田，當前地層滲透率相比水驅開發前地層滲透率發生了巨大變化。為使公式(6)中θ取值更加精確并且便于計算，將實驗數據重新整理，分別在(1 500～2 000)×10-3,(500～1 500)×10-3,(50～500)×10-3,(10～50)×10-3和(1～10)×10-3μm2的滲透率范圍內，通過最小二乘法依次做出在5種不同水質條件下，取負對數的巖心滲透率保留率隨無因次注入量變化的多條擬合直線。以滲透率為(1 500～2 000)×10-3μm2的巖心為例，圖中直線的斜率即為θ值。通過最小二乘法做出在5種不同水質下，滲透率的水質敏感系數的大小隨滲透率變化的多條擬合直線，并得到對應擬合直線的方程(圖8)。通過對全部實驗數據進行歸納，經線性插值與擴展，得到介于(1～2 000)×10-3μm2的滲透率所對應的θ值(表4)。

在確定的注入水水質和儲層滲透率下，根據表4做線性插值，可得目前儲層的水質敏感系數θ，將θ值帶入公式(6)，便計算出一定注水歷史后的儲層滲透率，為決策注水水質提供參數依據。

將表4中Ⅰ—Ⅴ級水質各滲透率對應的水質敏感系數θ，與現行的注水水質指標(表2)中各滲透率范圍相對應，將范圍下的水質敏感系數定義為水質準數θ′，其物理意義為在確定的注水水質和滲透率下，適合注入目標油層的最大界限θ值。經過計算出的值小于其相應的水質準數時，表明當前使用的水質與地層是匹配的，不需要考慮水質選擇問題。當計算出的值大于θ′時，則說明目前正在使用的水質已經與當前儲層不匹配，這個時候就需要根據對應的θ′，進行水質的重新選取。

4 考慮注水歷史的水質決策方法

在目標區塊注水過程中，以單井作為計算單位，進行水質決策方法的研究。在計算地層的水質敏感系數θ時，需明確單井儲層滲透率及當前所用水質。計算水質敏感系數之后，與相應的水質準數進行對比，用以判斷現在所用的水質能否適應當前儲層。

計算出的水質敏感系數小于相應的水質準數，則說明目前注入水水質符合水質標準。相對來看，如果大于的話，就需要考慮水質決策，具體注水水質決策的步驟如下。

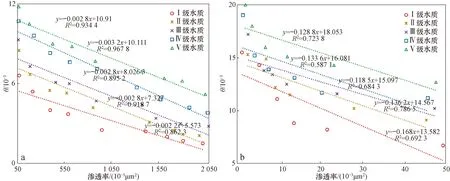
圖8 五種水質下水質敏感系數(θ)的大小隨滲透率變化擬合直線Fig.8 Fitting results of water quality-sensitivity coefficient changing with permeability under five types of injection water qualitya.滲透率>50× 10-3 μm2；b.滲透率<50× 10-3 μm2

表4 滲透率水質敏感系數(θ)取值Table 4 Water quality sensitivity coefficients of different permeability

1) 計算單井對應油層孔隙體積，如公式(7)所示。

φφi=Shφ

(7)

式中：V為單井儲層孔隙體積，m3；S為單井所控油層的供油面積，m2；h為油層有效厚度，m；φ為儲層平均有效孔隙度，%；i為注水井標號，i= 1，2，3，…，N。

2) 計算單井的無因次注入量，如公式(8)所示。

Qi=Qti/Vφi

(8)

式中：Qi為單井的無因次注入量，無量綱；Qti為單井從開始注水到目前累積總注水量，m3；Vφi為單井對應油層孔隙體積，m3。

(9)

考慮經濟因素的限制，為防止出現某一口井的水質不匹配，就更換整個注水系統水質的做法，當所控儲層的θ值大于對應的水質敏感系數θ′的井的數量大于整個注水系統所有井數量的1/2，此時再根據該水質決策方法重新選擇水質。

4) 計算當前整個目標區塊對應油層的平均滲透率。因不同井注水量不同，對儲層滲透率傷害程度不同，所以需要在取得各單井的月度注入情況報表的基礎上，依靠其中數據，統計目前各注水單井的實際注入量Qi，再通過公式(10)計算出該注水系統對應儲層的平均滲透率，再根據注水水質標準決定注水系統目前應該匹配哪種水質。

(10)

5) 在注水系統所對儲層的平均滲透率確定的情況下，結合注水水質標準，選擇目前注水系統適合的注水水質。

5 油田應用模擬

以孤東油田為例，該油田目前單元開發出現含水高、液量低與壓力高的特點。利用所建立的七區西單井注采模型，定壓差生產，壓差為2 MPa，進行產能預測，用以重新審視水質決策。模擬水驅前的地層平均滲透率約為2 000×10-3μm2，研究注入不同水質下的儲層滲透率及產能變化情況，為水質決策方法提供論證。

綜上所述，注入不同級別的注入水對儲層滲透率的改變情況不同。從衰減情況看，當注水達到20 a左右時，Ⅴ級水質下的儲層滲透率呈現明顯的下降；在注水達到50余年后，滲透率下降速度開始逐漸變慢，最終下降至580×10-3μm2左右。水驅的過程中如果堵塞達到了一定的程度，注入水中的污染物很難繼續進入儲層，造成滲透率下降變緩的情況，甚至有些情況下會發生“憋縫”，出現儲層滲透率增大的假象。

注水40 a后，通過線性差值可得θ值為0.005 31，當前累積注水量38 ×106m3，計算當前單井儲層孔隙體積為306×103m3，當前單井無因次注入量為124 PV，當前滲透率為1 034.687×10-3μm2，水質準數θ′為0.006 8，因此需要進行更換水質的重新決策。依靠行業注水標準表1可知當前應選用Ⅳ級水質進行生產。通過圖9可以看出，當注水達到40年左右，從Ⅴ級水質換到Ⅳ級水質后，繼續進行注水，產量相應增加。如圖10所示，累積產油量增加了約2.5×104m3，采收率提高了1.3%。然而若繼續更換較好的水質，產能雖然得到提高，但效果接近Ⅳ級水質，這時候考慮到經濟因素，選擇Ⅳ級水質最為合適。

6 結論

1) 水質一定下，巖心的K越高，K/K0下降越慢；K越低，K/K0下降越快。對于高滲巖心，水質的影響比較大，當無因次注入量在200 PV時，Ⅰ級水質中高滲巖心滲透率保留率會在0.7左右，而在Ⅴ級水質中則是處于0.3左右。對于滲透率略低的巖心，水質因素的影響較小，K/K0會快速下降到一個較低的水平。

2)K/K0與無因次注入量Qi的關系公式,可用于重新審視水質與地層滲透率的匹配關系，進而定量計算和預測一定注入歷史下具體注水層的滲透率。

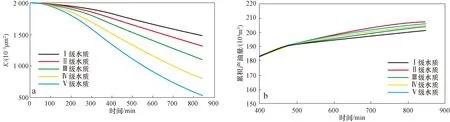
圖9 滲透率為2 000× 10-3 μm2的儲層在不同水質條件下滲透率與產量的變化情況Fig.9 Change of permeability and production with time for reservoirs with a permeability of 2 000×10-3 μm2 under different injection water qualitya.滲透率變化情況;b.產量變化情況

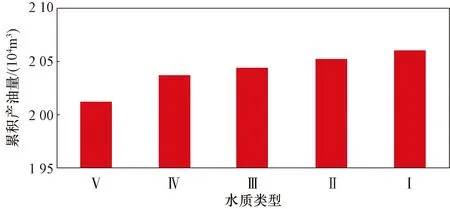
圖10 五種不同級別水質條件下累積產油量對比Fig.10 Comparison of cumulative oil production from reservoirs flooded with water of different quality

3)在定量表征數學模型基礎上，定義地層滲透率的水質敏感系數θ，確定了注水決策界限為11.9～13.4,7.2～13.2,6.6～9.2,5.3～8.5和5.3～6.7。以此作為與儲層相適應的水質選取標準，為水質決策提供了參數依據，通過水量加權確定儲層平均滲透率，形成水質決策方法。