帶有擾動的變時滯離散系統可達集估計

莊 蘇，叢玉豪,2

（1. 上海大學 理學院，上海 200444；2. 上海海關學院，上海 201204）

可達集估計是控制理論中一個重要的研究課題，它在許多領域有著廣泛的應用，如安全檢查[1]、峰間極小化[2]、參數估計[3]和具有飽和執行器的控制系統[4]。系統的可達集是指從初始條件出發，能夠到達的所有系統狀態的集合。通常人們很難獲得可達集的精確特征，所以，需要確定一個能夠界定可達集的區域，并且希望這個區域能夠盡可能的小，這就是可達集估計問題。

眾所周知，在工程和實際系統中，一方面，由于數據變換、測量誤差、線性化近似等原因，擾動輸入現象是不可避免的。對于具有有界峰值擾動的系統，研究可達集估計問題的最新方法之一就是橢球體技術，其目的是確定包含可達集的橢球體。Boyd等[1]提出，這種橢球可以通過使用Lyapunov方法和線性矩陣不等式（LMI）技術獲得。

另一方面，在各種實際系統中，時滯經常發生，它的存在可能導致系統不穩定[5]。然而目前對于時滯系統可達集的研究還比較少。因此，如何找到一個盡可能小的估計來界定時滯系統的可達集引起了許多學者的關注[6-12]。Fridman等[6]采用Lyapunov-Razumikhin方法研究了帶有有界峰值擾動的時變時滯連續線性系統的可達集估計問題；Kim[7]改進了Fridman等的研究成果，通過建立適當的Lyapunov-Krasovskii泛函，提出了一個改進的可達集橢球界，其中時滯相關條件以僅涉及一個非凸參數的矩陣不等式形式給出；Zuo等[8]提出了一種用于多面體不確定系統可達集估計的極大Lyapunov-Krasovskii泛函方法；Nam等[9]認為時滯下限不必為零，提出利用時滯分解技術來估計可達集。

值得注意的是，上述文獻中考慮的系統都是連續的。實際上，隨著計算機技術的發展，大多數控制工程應用系統都是數字實現的。因此，直接對離散模型進行研究更為合理。到目前為止，對于離散時滯系統的可達集估計問題的研究還很少。That等[10]討論了受狀態時滯和有界擾動的線性離散系統的可達集有界問題，提出了一種新的極軸投影的概念；Lam等[11]研究了具有有界擾動和多重常時滯的離散多面體系統的可達集估計問題。但是上述結果僅僅針對開環系統，而對于系統可達集估計的控制器設計問題研究成果較少。比如，Zhang等[12]研究了具有分布時滯的連續系統的控制器設計問題；Chen等[13]研究了離散線性切換系統的狀態反饋控制器設計問題，但并未考慮時滯對系統可達集估計的影響。但有關利用反饋控制器來研究離散變時滯系統的可達集估計問題還未被涉及。此外，上述文獻都假設系統的初始值為零，這個條件在可達集估計的過程中帶來了一些限制。

本文在有界擾動下，研究了一類變時滯離散系統的可達集估計和控制器設計問題，其中系統的初始值不再要求為零。利用Lyapunov-Krasovskii泛函方法，得到界定閉環系統可達集的充分條件。之后，通過求解優化問題，確定了一個盡可能小的區域來估計系統的可達集，最后給出兩個仿真實例驗證所得結果的有效性。

1 問題描述

考慮變時滯離散系統

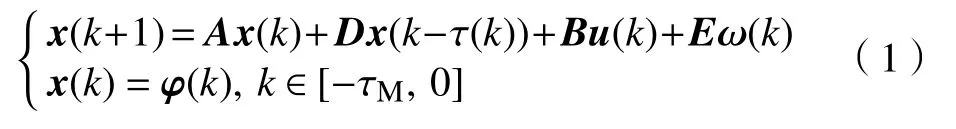
式中：x(k)=[x1(k),x2(k),···,xn(k)]T∈Rn為系統的狀態向量；u(k)為輸入向量；A,D,B和E為適當維數的常矩陣；τ(k)為時變時滯，且滿足0＜τm≤τ(k)≤τM，τm,τM為非負整數。

初始條件 φ(k)滿足

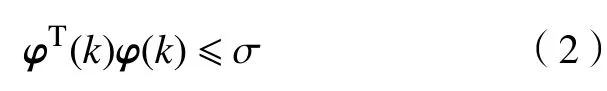
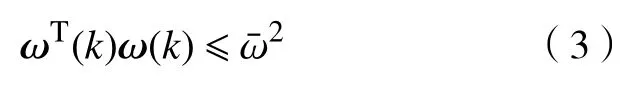
定義1在有界擾動下，系統（1）的可達集為

定義2對于矩陣P＞0，橢球的定義如下

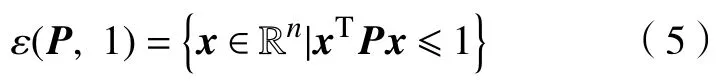
對于系統（1），考慮如下形式的狀態反饋控制器

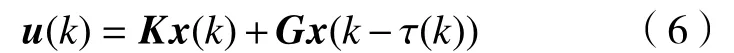
式中，K和G為待定控制器增益矩陣。

將狀態反饋控制器式（6）代入系統（1），可得如下閉環系統

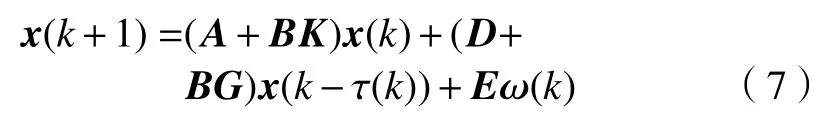
定義3令，稱,λ1,λ2,···,λn是A的特征值}為矩陣A的譜半徑。若ρ(A)＜1，則稱矩陣A是Schur穩定的。

本文的主要目的是設計一個狀態反饋控制器，使閉環系統的可達集包含在橢球體中，并且橢球體盡可能小。因此，為了得到本文主要結果，首先給出引理1和引理2。

引理1[14]設V(x(k))是滿足的Lyapunov泛函，且V(x(k))＞0。若存在標量0＜α＜1使得

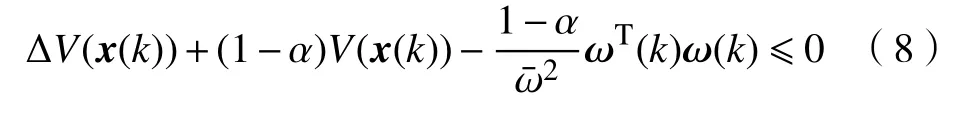
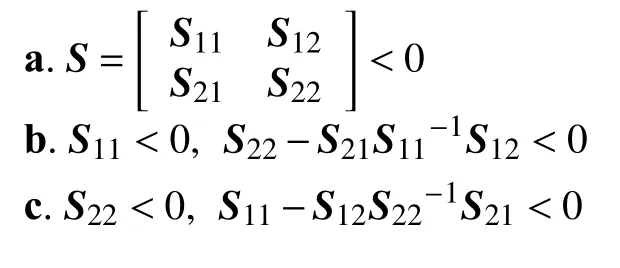
2 主要結論

2.1 可達集的橢球界

本文旨在設計一個狀態反饋控制器（6），使得閉環系統（7）的可達集包含在橢球里面，并且該橢球要盡可能的小。以下定理給出系統（1）～（3）可達集橢球界存在的充分條件。

定理1考慮在有界峰值擾動（3）下的系統（7），若存在正標量λ1,λ2,λ3,λ4，矩陣＞0，＞0，＞0，＞0,L,R及標量0＜α＜1，滿足

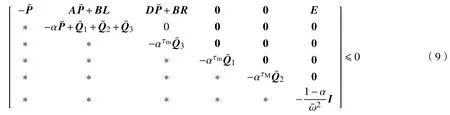
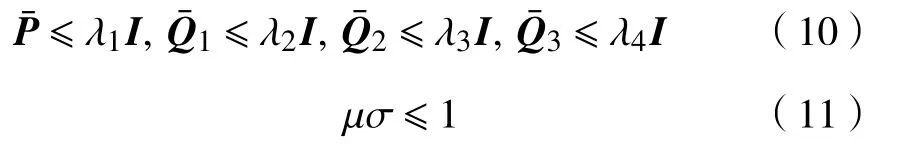
其中

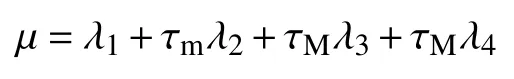
那么，存在狀態反饋控制器（6），使得閉環系統（7）的可達集包含在橢球中。

證明選取如下Lyapunov-Krasovskii泛函：

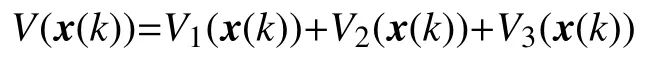
其中

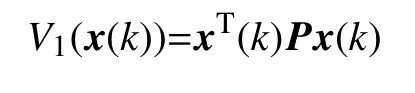
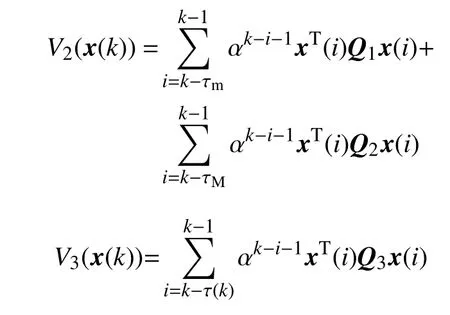
定義 ΔV(x(k))為V(x(k))的向前差分，則

不論是硬件方面在全市率先定標檢測室樣板間，還是軟件方面創新開發APP及政府文化建設，江岸食藥監局始終不忘初心，以歸零心態重新出發，奮力拼搏趕超，農殘檢測工作再次走在全市前列。

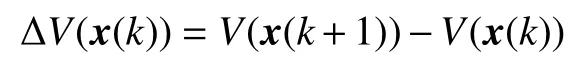
那么

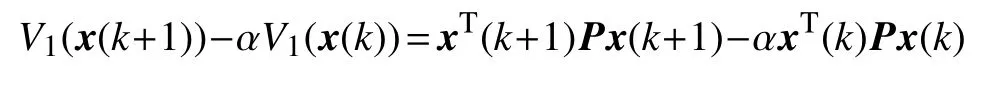
為了簡便，式（8）記為

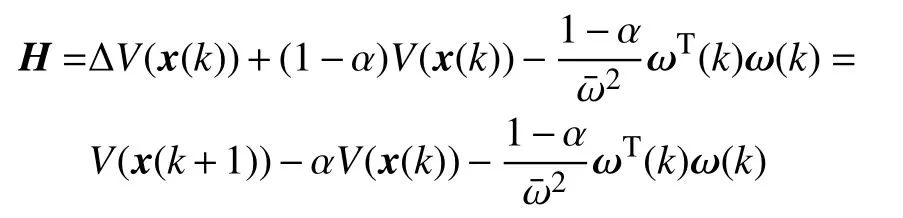
運用引理1，可得

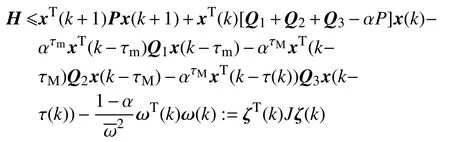
其中

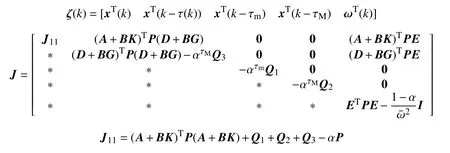
若J≤0，運用Schur補引理，可得

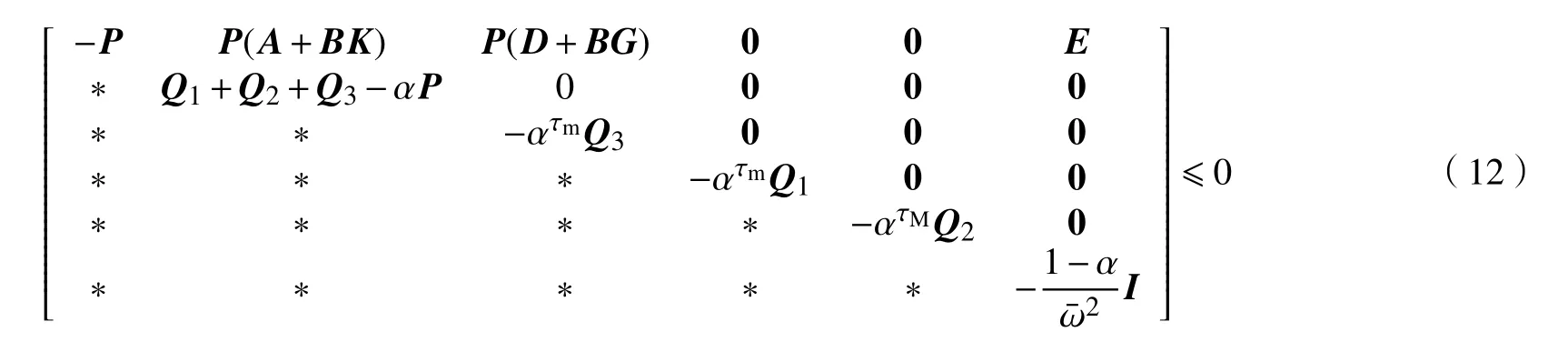
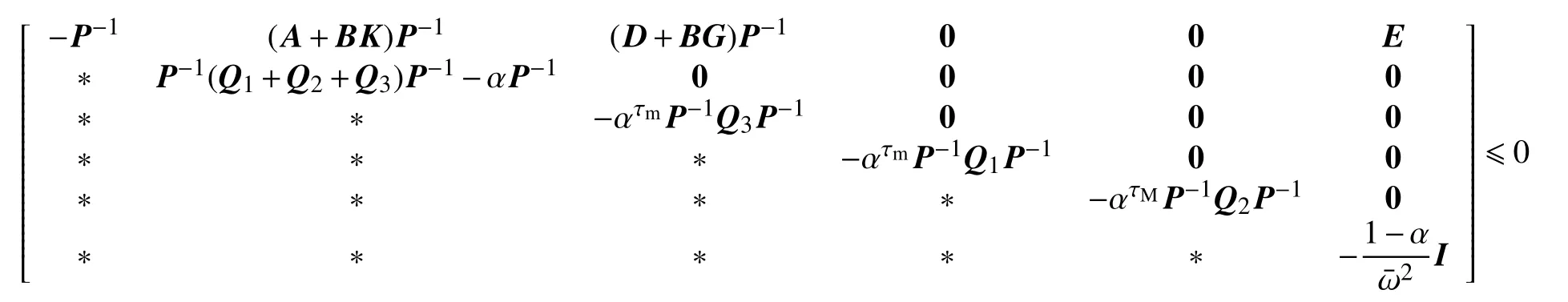
進一步，考慮Lyapunov泛函初值V(x(0))

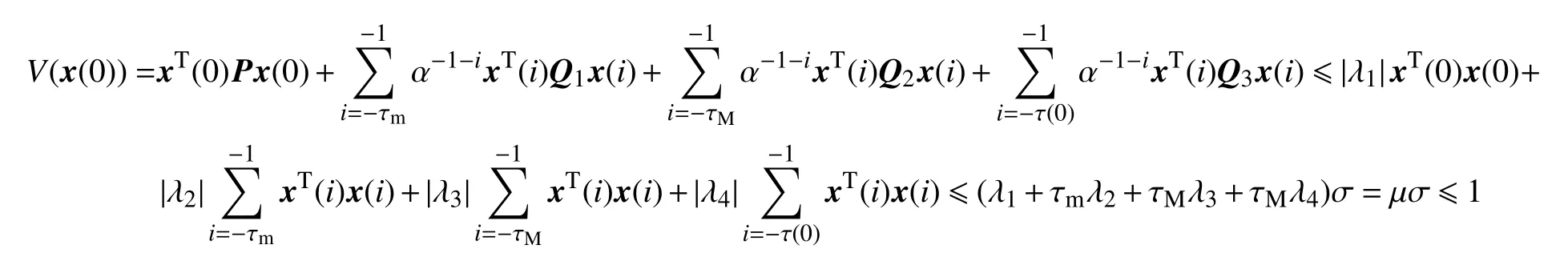
由條件（10）～（11）和引理2可知，

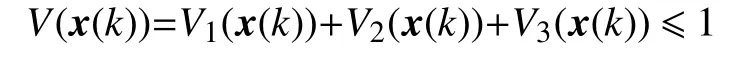
由于V2(x(k)),V3(x(k))≥0，所以V1(x(k))≤1。即，xT(k)Px(k)是橢球ε(P,1)的內部。由此可以得出結論：系統（7）的可達集包含在ε(P,1)中。定理1證畢。

在狀態反饋控制器設計過程中，開環系統不一定穩定，只需滿足定理1中的相關條件，就可以為系統設計控制器，得到穩定的閉環系統。

定理1中得到的條件不是LMI，因為它包含決策變量的乘積。然而，如果標量 α是固定的，則式（9）中的條件對于矩陣變量也是線性的。

為了求解帶有參數λ1,λ2,λ3,λ4的矩陣不等式式（10），首先要將其轉化為LMIs的形式。例如，不等式可表述為線性矩陣不等式，記=diag(λ1,λ1,···,λ1)。其中被定義為一個矩陣變量，并且依賴于決策變量λ1。

系統（13）優化問題可以轉化為

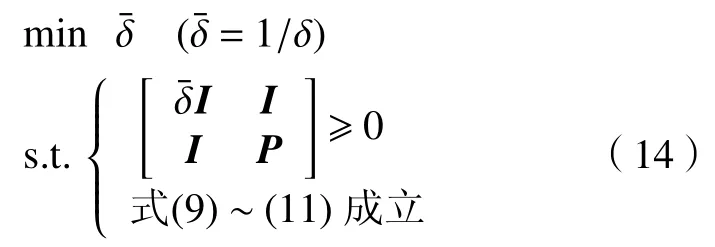
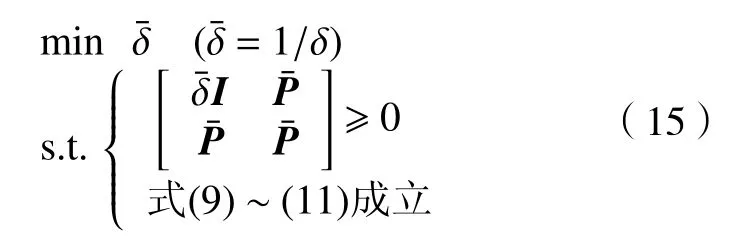
2.2 算法描述

定理1給出了有界擾動下閉環系統的可達集的界定條件，通過上述優化方法可以對邊界橢球進行優化。然而，定理1中的結果是一個包含非凸標量 α時滯相關的矩陣不等式，通過固定α，可以使該問題轉化為求解線性矩陣不等式（LMI）。

為了獲得可達集的最小橢球，必須確定最優的標量α，這可以通過遺傳算法（GA）來實現。算法如下：

a. 在（0, 1）中隨機生成α，每個 α都是GA種群的一個個體；

b. 對于每個α，利用mincx. 求解包括變量的LMI優化問題，得到最優的；

c. 設置最大代數，如果達到該數字，則GA終止，否則，繼續GA過程；

d. 根據每個α 的適應值，以概率選擇下一代個體；

e. 根據給定的概率對新一代進行交叉和變異操作；

3 數值算例

本節給出兩個數值實例來驗證結果的有效性。

例1考慮時滯離散系統（1），系統參數為

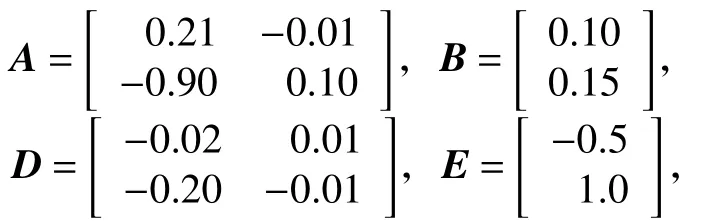
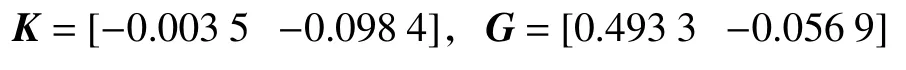
由定理1得到的邊界橢球以及閉環系統的狀態如圖1所示。由圖可見，閉環系統的狀態包含在橢球ε(P,1)中。

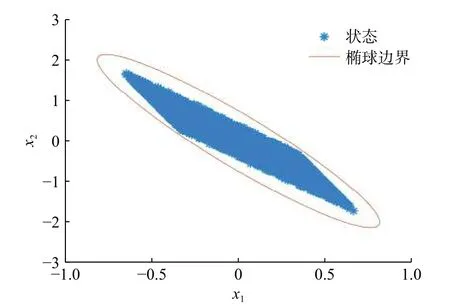
圖1 可達集和橢球邊界（例1）Fig.1 Reachable set and ellipsoidal bound (Example 1)

例2 考慮時滯離散系統（1），系統參數如下：

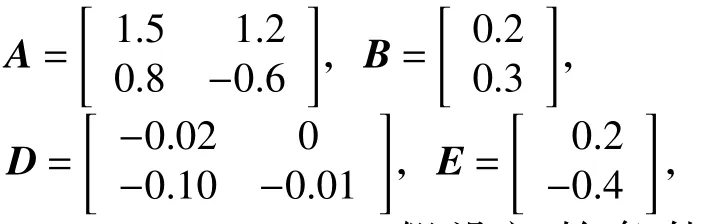
注意到，例2中A不是Schur穩定矩陣，因此開環系統的可達集不能被任何橢球體所界定。所以可以通過設計狀態反饋控制器，處理閉環系統的可達集估計問題。

通過求解優化問題（15），計算結果如下：

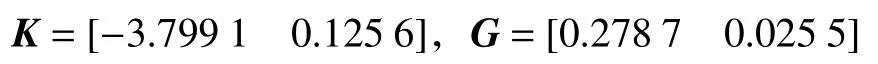
由定理1得到的橢球邊界以及閉環系統的狀態如圖2所示。由圖可見，閉環系統的狀態包含在橢球ε(P,1)中。

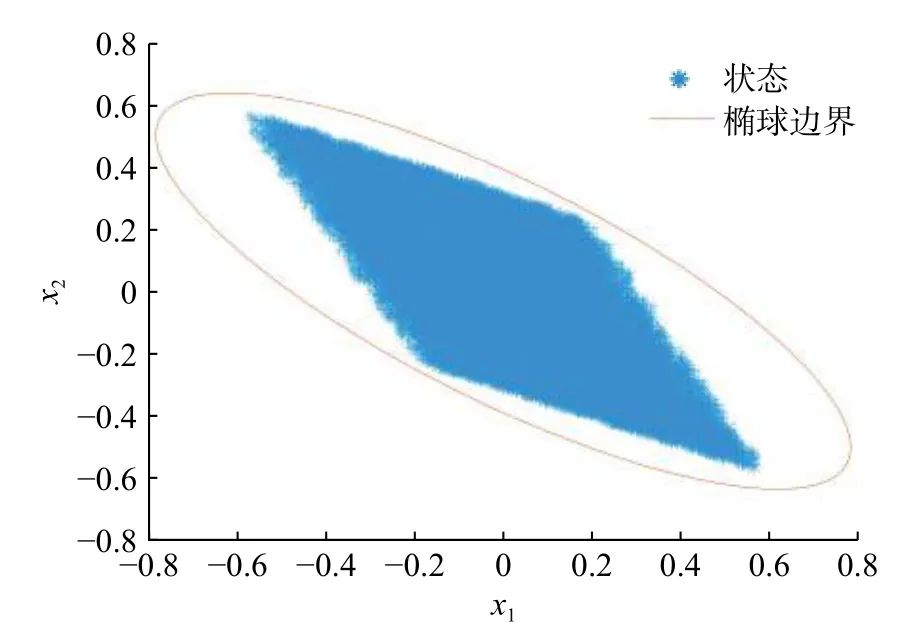
圖2 可達集和橢球邊界（例2）Fig.2 Reachable set and ellipsoidal bound (Example 2)

4 結 論

研究了在有界峰值擾動下離散變時滯系統的可達集估計問題，且系統的初值不必為零。通過設計狀態反饋控制器，將系統由開環系統轉化為閉環系統。隨后，利用Lyapunov-Krasovkii泛函方法給出了閉環系統可達集的橢球邊界。為了使該橢球體盡可能小，提出了優化方法。在此過程中，采用遺傳算法求解最優參數，數值算例驗證了本文所得結果的有效性。