修正的變分迭代法在四階Cahn-Hilliard 方程和BBM-Burgers 方程中的應用*

鐘鳴 田守富 時怡清

(中國礦業大學數學學院,徐州 221100)

變分迭代法是一種基于變分原理,具有高數值精度的數值格式,目前已廣泛應用于各類強非線性孤立波方程的數值求解中.本文利用修正的變分迭代法對兩類非線性方程進行研究.該格式是對原數值方法的一種改進,即在變分項前引入了參數h.通過定義誤差函數的離散二范數并在定義域內繪出h-曲線,從而確定出使誤差達到最小的h,再返回原迭代過程進行求解.同時,參數的引入也擴大了原數值解的收斂域,在迭代次數一定的情況下達到了數值最優.在數值實驗中,將上述結果應用于四階的Cahn-Hilliard 方程和Benjamin-Bona-Mahoney-Burgers 方程.對于四階的Cahn-Hilliard 方程,普通的變分迭代法絕對誤差在 1 0?1 左右,經過修正后,絕對誤差降為 1 0?4,而且修正后的方法擴大了原數值解的收斂域.對于Benjamin-Bona-Mahony-Burgers 方程,利用帶有輔助參數的變分迭代法將數值解的精度提高到 1 0?3,對真解的逼近效果優于原始的變分迭代法.此數值方法也為其他強非線性孤立波微分方程的數值求解提供了方法和參考.

1 引言

非線性科學作為現代數學物理的一個重要組成,具有廣泛的分支.如非線性場論[1]、玻色-愛因斯坦凝聚物[2]、孤立波理論[3,4]、非線性光學[5,6]等.而非線性發展方程本身的物理背景和孤立波解的特殊性質使得孤子理論成為當前科學發展的前沿和熱點問題.目前,已經發展出了多種多樣的用來處理各種可積方程的解析方法,如Fokas 方法[7,8]、反散射變換[9?11]、達布變換[12,13]等.最近,光孤子的出現也引起了一大批學者的關注[14?17].但是由于發展型方程的強非線性,解析方法不總是適用的.因此數值方法的出現大大促進了孤立子理論和非線性物理的發展.如楊建科[18]提出的平方迭代算法來進行孤立波的穩定性分析得到了廣泛的應用;Bao 和Yin[19]利用四階時間分裂傅里葉譜方法研究了Diarc 方程,也被推廣到其他非線性方程中;Antoine 等[20]使用數值方法研究了非線性薛定諤方程的動力學性質;Cockburn 和Shu[21]以及Jiang 和Shu[22]率先提出了間斷有限元和加權無本質振蕩(WENO)等方法,極大豐富了數值求解偏微分方程的格式.

本文要介紹的變分迭代法與上述幾種傳統的數值求解方法相比,有著求解過程靈活、收斂速度快、數值精度高等優勢.He[23]首次提出了變分迭代法,并對變分迭代方法進行了非常清晰的討論.同時該方法也被推廣到各類積分-微分方程[24,25]的數值求解中.Hesameddini 和Latifizadeh[26]使用Laplace 變換重構了變分迭代算法;Salkuyeh[27]證明了變分迭代算法的收斂性.至此,變分迭代法的基本理論已經成形.Noor 和Mohyud-Din[28]利用He’s 多項式對變分迭代法進一步改進,該方法將變分迭代法與同倫攝動法[29]進行結合,大大提高了數值精度;Zayed 和Rahman[30]利用改進后的變分迭代法研究了KdV 方程和Wu-Zhang 方程的數值解,說明了變分迭代法在處理高維問題上的優勢.

本文第2 節簡要介紹原始變分迭代法的原理以及求解過程;第3 節重點介紹帶有參數攝動的修正變分迭代法[31],該方法通過在變分項前引入參數h,從而對原始數值算法進行改進,提高了格式的收斂性;第4 節和第5 節將上述方法應用到兩類強非線性孤立波微分方程中,其逼近效果理想,且與問題的物理性質兼容.

2 變分迭代法

考慮一般的微分方程

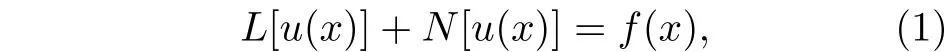
其中L[u(x)]和N[u(x)] 分別代表線性項和非線性項,f(x) 為已知函數.變分迭代法的主要思想是為(1)式構造一個校正泛函如下.

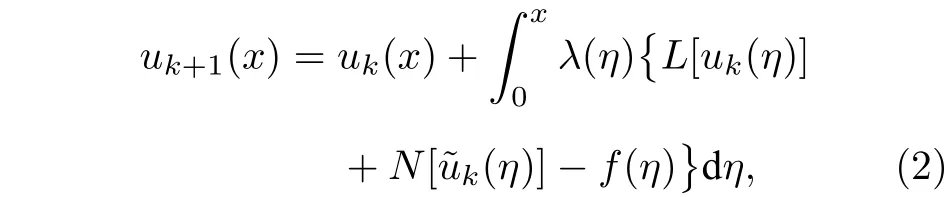
其中λ(η) 稱為廣義的拉氏乘子,可以用變分理論最佳識別.對(2)式兩邊同時對uk(x) 取變分δ,即

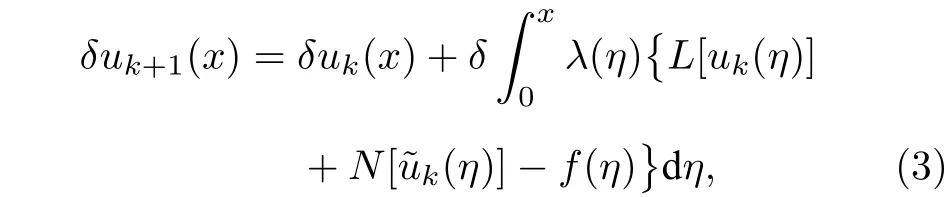
簡而言之,方程(1)的求解過程如下,給定初值u0(x),

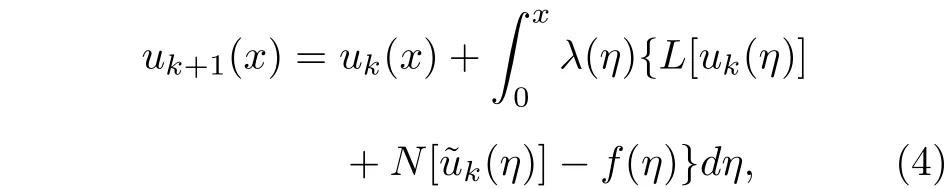
其中k0,1,···,進行迭代計算.

上述通過迭代算法得到解的方法便稱為變分迭代法.

3 修正的變分迭代法

可以將未知的輔助參數插入到變分迭代算法(4)式中,則算法修正如下:

給定初值u0(x),通過以下迭代式進行計算

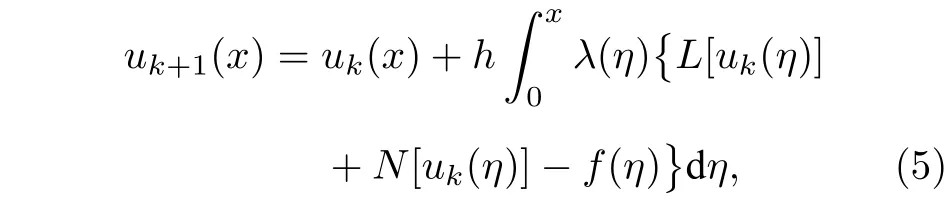
其中k0,1,···.通常會采取截斷解uk(x,t,h),其中含有輔助參數h,它保證了數值精度、收斂速度以及收斂域,這種方法被稱為帶有輔助參數的變分迭代算法.該格式的最大優點是簡便,并且能在較大的收斂域中對原方程進行近似.通常,可通過誤差函數在給定的區域內根據二范數畫出h曲線,從而確定出h的最佳取值,再將h代入到迭代算法(5)式中進行求解.

4 四階Cahn-Hilliard 方程

考慮如下的四階Cahn-Hilliard 方程:

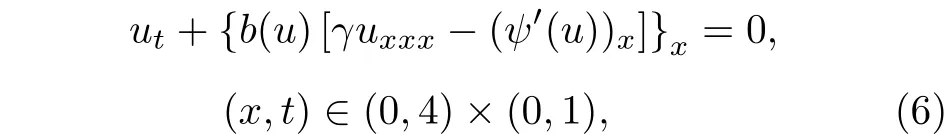
同時給定初值u(x,0)u0(x).其中ψ(u) 是關于u的光滑函數,一般為非線性.四階Cahn-Hilliard方程是Cahn 和Hilliard[32]在1958 年研究二元合金的分離現象時首次提出的.隨著現代科學技術的不斷發展,該方程的應用越來越廣泛,例如多相流中的界面動力學.一些學者利用經典的數值方法對四階Cahn-Hilliard 方程進行求解,例如有限元方法[33]、間斷有限元法[34]、多重網格法[35].本文的主要工作是通過修正的變分迭代法對四階Cahn-Hilliard 方程進行數值求解,并且與原始的格式進行了對比.

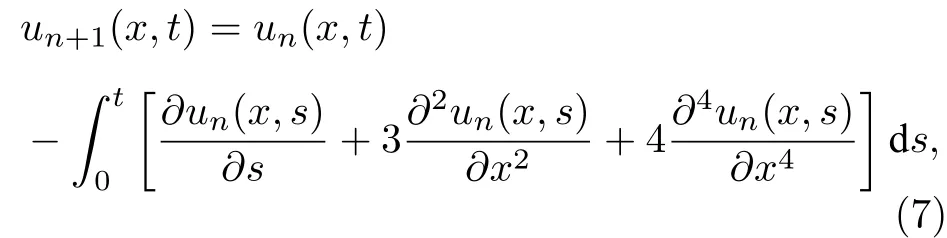
取上述初值后便可以進行計算求解.通過迭代求解,圖1 給出了u10(x,t) 的絕對誤差圖像.

由圖1 可以看出,在x和t較大時,誤差會偏大.如果繼續執行迭代過程,則可以提高精度;當n趨向無窮大時,可以獲得精確解.

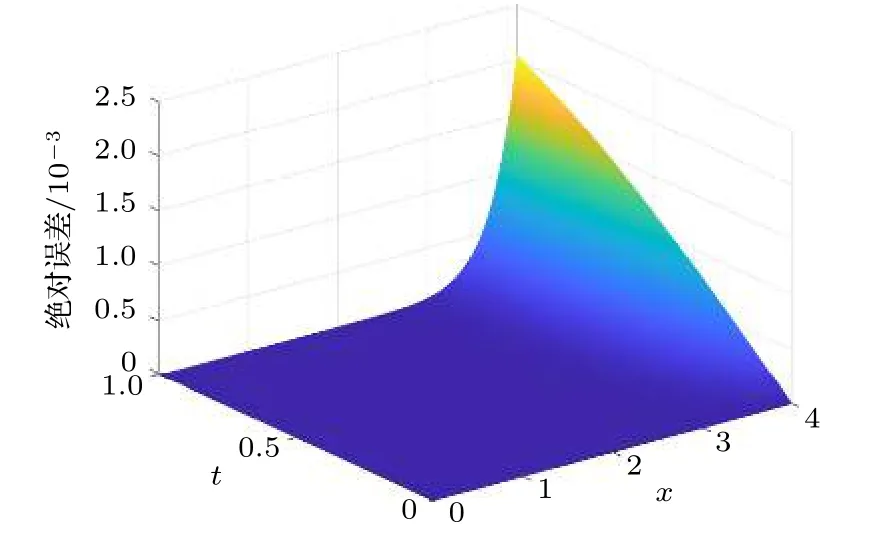
圖1 原始算法的誤差Fig.1.Error of the original algorithm.

利用帶有輔助參數的變分迭代法,得出以下迭代公式

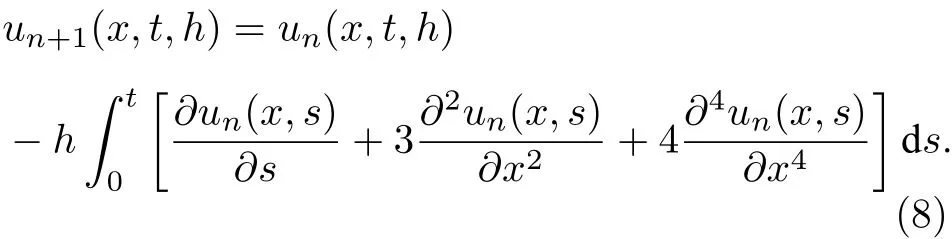
下面通過方程定義誤差函數如下:

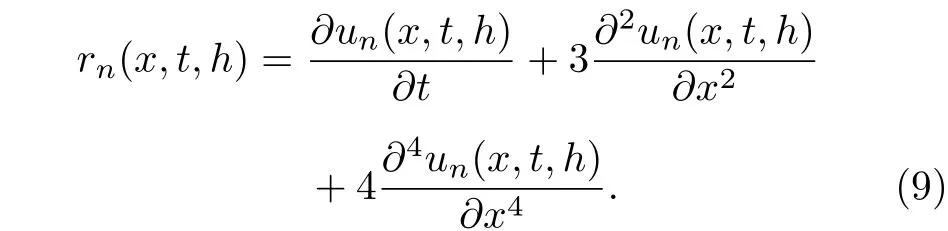
為了找到一個合適的參數h,圖2 給出了誤差函數在離散網格上的二范數.其中,離散后的誤差函數的二范數定義為

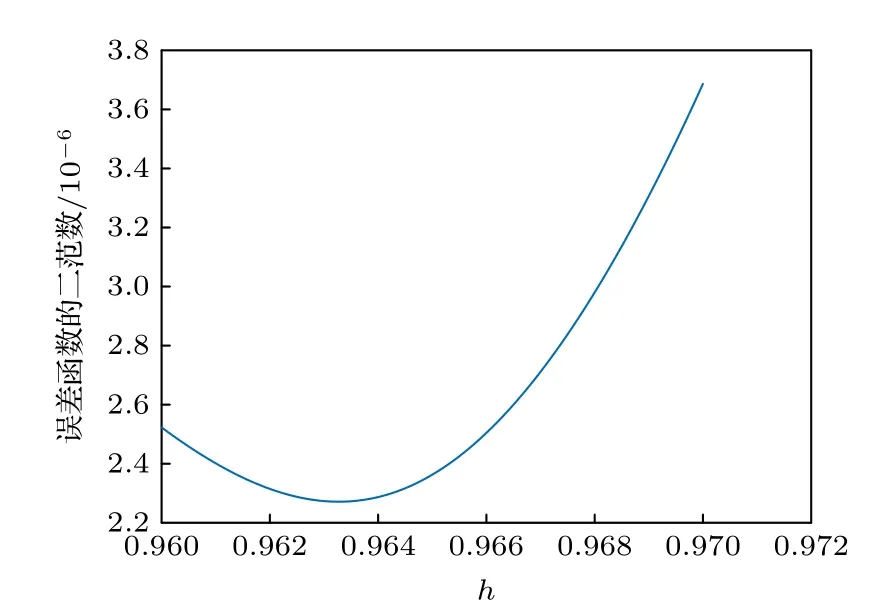
圖2 h-曲線Fig.2.h-curve.

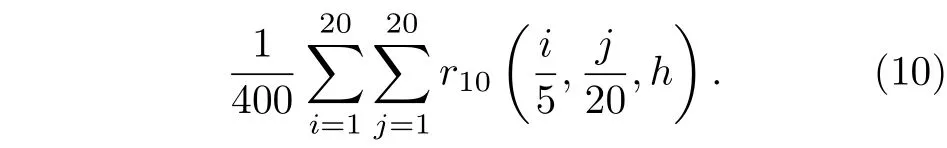
根據圖2,選取h0.963575 作為輔助參數,將其代回到(8)式進行迭代求解.結果與真解之間的絕對誤差如圖3 所示.可以看出,帶有輔助參數的變分迭代法不僅擴大了收斂域,同時提高了數值精度.

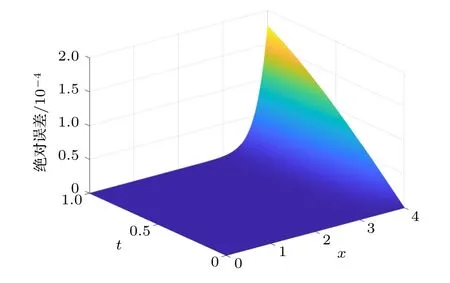
圖3 帶有參數的算法的誤差Fig.3.Error of algorithm with parameter.

圖4 和圖5 分別給出了區域內的真解與數值解圖像.

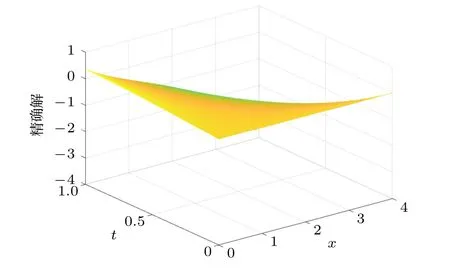
圖4 精確解Fig.4.Exact solution.

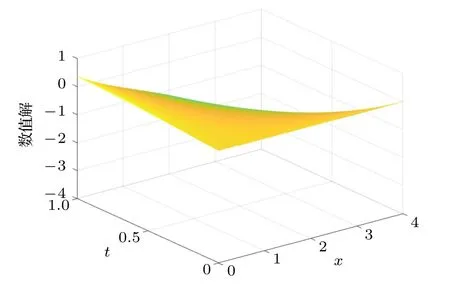
圖5 數值解Fig.5.Numerical solution.

圖6 中,固定x4,給出了數值解與真解的剖面圖對比.

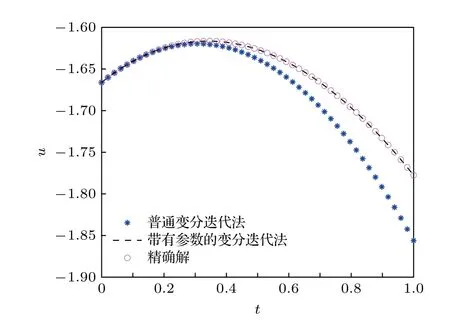
圖6 x=4 時原方法和修正后方法的數值解以及真解的圖像Fig.6.The numerical solution of the original method and the corrected method,as well as the image of the exact solution when x=4.

5 Benjamin-Bona-Mahony-Burgers(BBM-B)方程

Benjamin-Bona-Mahony-Burgers (BBM-B)方程表示為

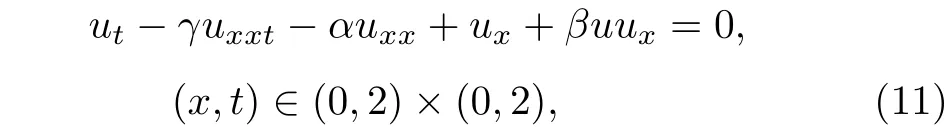
給定初值為u0(x).其中α,β,γ為已知常數.上述方程由 Benjamin 等[36]提出并研究,用于研究均勻水槽中小振幅水波的行為.其中,u(x,t) 代表水平x方向上的流體速度.作為特殊情況,這些方程包括非線性擴散模型的Burgers 方程和非線性分散介質中的長波模型的BBM 方程.Karakoc 和Bhowmik[37]利用B 樣條的伽遼金有限元方法進行了數值模擬.

在本文的數值實驗中,取α1,β12,γ1,,該問題有以下精確解:

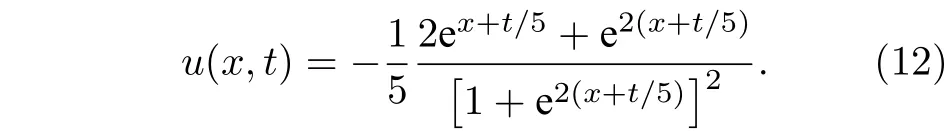
原始的變分格式可以利用以下迭代公式進行求解:

圖7 給出了給定區域內u4(x,t) 的誤差圖像.在x和t偏小的情況下,誤差不會增加很快;但是當x和t增大時,誤差會迅速增長到 10 左右.從圖7不難得出以下結論:原始的變分迭代法對于真實解的逼近效果較差,而且在增加迭代次數的情況下,會出現數值不穩定的情況.

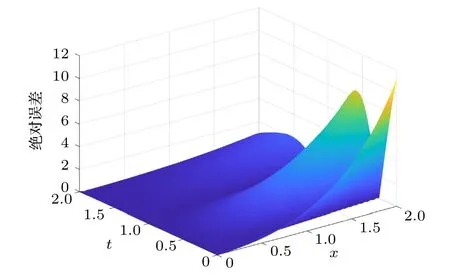
圖7 原始算法的誤差Fig.7.Error of the original algorithm.

故下面采用參數攝動的變分迭代法進行數值求解.迭代公式為

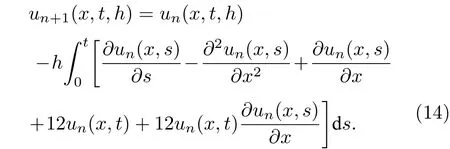
通過參數的引入,本文通過誤差函數定出h的最佳取值.誤差函數定義如下:

引入節點后,h曲線給出了h的局部最佳取值.定義誤差函數的二范數如下:

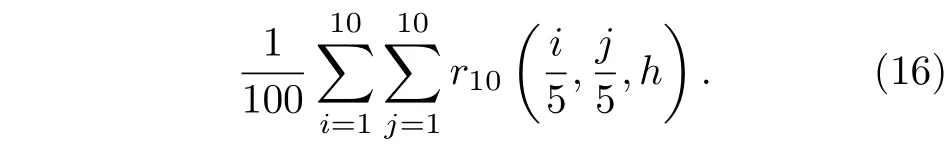
從圖8 可以看出,當h0.1037 時,整體誤差達到極小值.故在(14)式中取h0.1037,進行迭代求解.圖9 給出了改進得到的數值解與真解之間的誤差,不難看出帶有參數攝動的數值格式大大降低了數值解的誤差,絕對誤差降低到 1 0?3,對真解的逼近達到了理想效果.區域內不同點的真解和數值解值如表1 所列.圖10 和圖11 給出了數值解和真解的圖像對比.

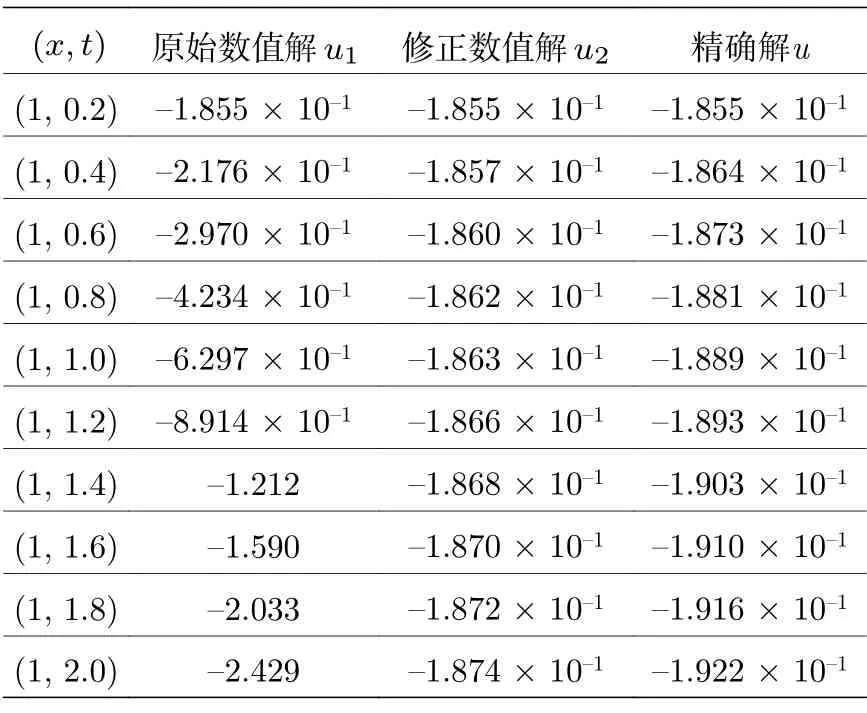
表1 不同點處真解與數值解對比Table 1.Comparison of true and numerical solutions at different points.

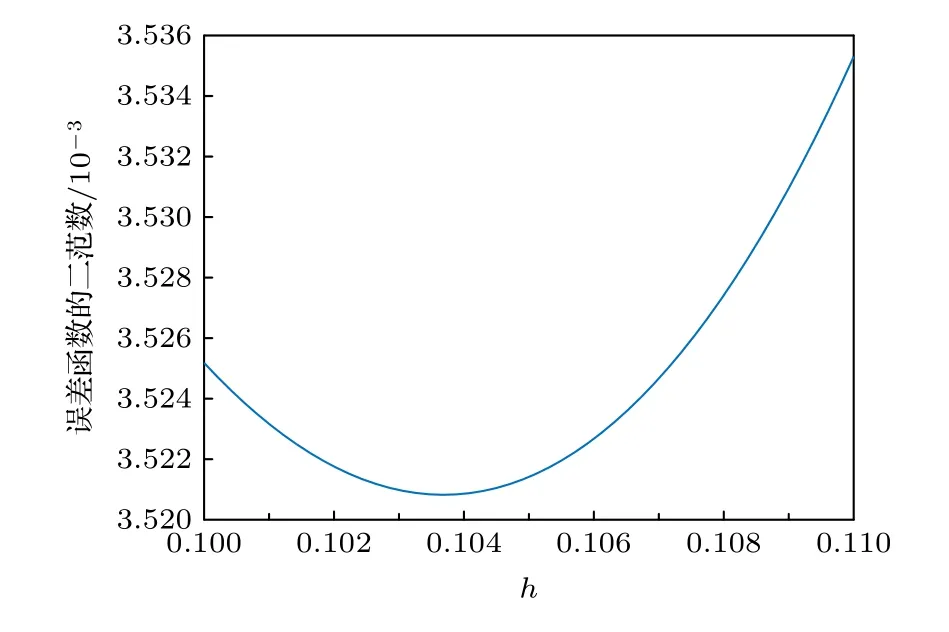
圖8 h-曲線Fig.8.h-curve.

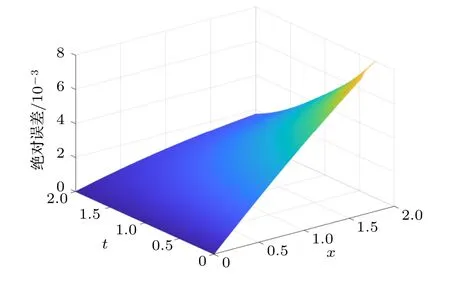
圖9 帶有參數的算法的誤差Fig.9.Error of algorithm with parameters.

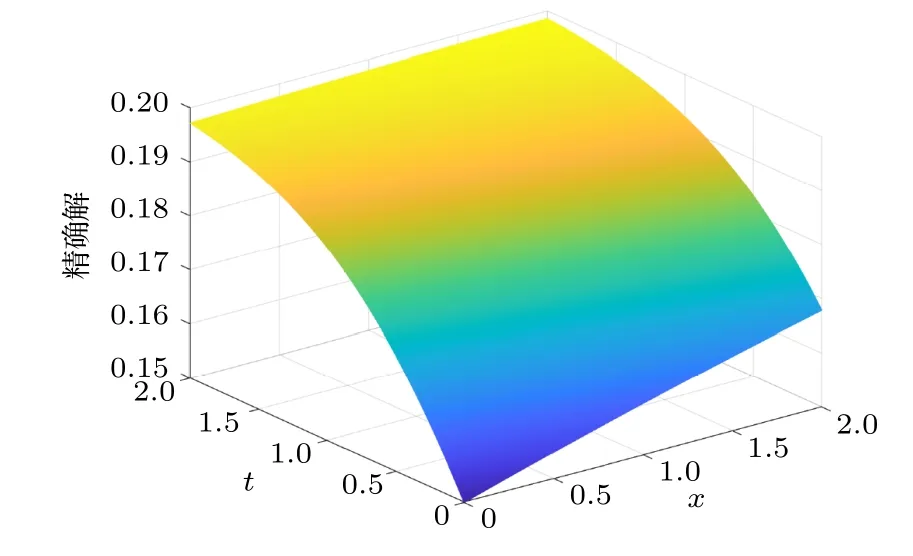
圖10 精確解Fig.10.Exact solution.

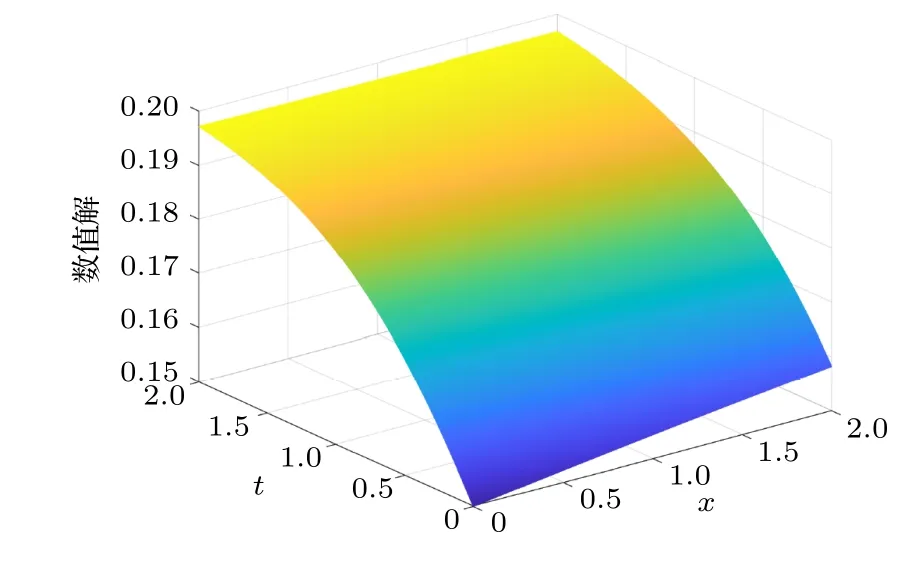
圖11 數值解Fig.11.Numerical solution.

6 結論

本文使用具有輔助參數的變分迭代算法可以解決四階的Cahn-Hilliard 方程和BBM-B 方程的數值解問題.具有輔助參數的變分迭代算法在應用,計算精度與效率等方面具有明顯的優勢.其中輔助參數可以通過h曲線和殘差函數的2 范數的誤差來確定.圖形和數值結果表明,帶有參數攝動的變分迭代算法適用于物理科學和工程學中出現的大部分線性和非線性問題,優于原始的變分迭代算法.

感謝中國礦業大學數學學院楊金杰博士的討論.