一類超混沌系統的動力學分析及電路實現

宋 爽，湯 瓊，瞿民凱，趙思遠

（湖南工業大學 理學院，湖南 株洲 412007）

1 背景知識

1979年，學者O.E.R?ssler首次發現了一個可以同時產生兩個方向上雙曲不穩定的混沌奇異吸引子的四維動力學系統[1]，并將之命名為超混沌現象。相較于常見的三維混沌系統，超混沌系統在實際應用中更能滿足通信保密、圖像加密、人工神經網絡、非線性電路等領域的需求。超混沌系統可以通過引入新的狀態變量反饋或基于憶阻器元件實現，得到四維及以上的高維動力學系統[2-5]，并通過改變非線性項取值范圍或憶阻器的控制參數，獲得倍周期分叉、單渦卷吸引子、雙渦卷吸引子、單方向多渦卷吸引子，甚至網格多渦卷吸引子等混沌現象，現已成為混沌系統中極具研究價值的一個方向。

相較于低維混沌系統較為簡單的動力學特性和不夠多的密鑰參數，超混沌系統具有更復雜的動力學特性和更豐富的密鑰參數。判定一個動力學系統是否為超混沌系統，最直觀的判斷標準就是具有兩個或兩個以上的正Lyapunov指數。

近幾十年來，國內外學者一直在研究生成超混沌系統的方法。受學者Li Q.D.[6]發現超混沌Chen系統的啟發，科研工作者們多通過引入新狀態變量反饋法生成超混沌系統[7-14]。由于引入狀態變量的反饋控制器多為非線性項，它可進一步豐富動力學系統的混沌特征，增加系統的不可預測性。該系統的電路實現取決于反饋量非線性項的復雜程度，如何找到簡單且易實現的超混沌系統一直是混沌電路的研究目標。

雖然關于超混沌系統的構造已經有了大量的研究，但是由于混沌吸引子較為復雜的動力學特性，現有關于多渦卷混沌系統電路實現的報道仍然比較少。因此，對不同非線性控制函數構造的超混沌系統進行詳細的動力學分析，并搭建出對應的電路模型，是十分必要的。因此，本研究在三維Lü系統[7]的基礎上加以修改，構建了一個基于狀態變量反饋的四維動力學系統，經計算Lyapunov指數后，證實其為超混沌系統。然后，對其進行了基本的平衡點穩定性分析、耗散性分析、對稱性分析等動力學分析，并通過計算Lyapunov指數及維數、繪制Poincaré截面圖等方法對該超混沌系統進行了數值仿真分析。最后，根據反相器、積分器等基本的運算放大電路搭建出其相應的電路模型。本研究基于憶阻器反饋設計新的超混沌系統，該方法在增加系統維度的同時豐富了系統的混沌特征，且對應的混沌電路設計更易實現，本研究可為混沌系統的電路實現提供參考。

2 超混沌系統的數學模型

在三維Lü系統基礎上進行修改，構建了一個基于狀態變量反饋的四維動力學系統，新的超混沌系統的狀態方程如下：

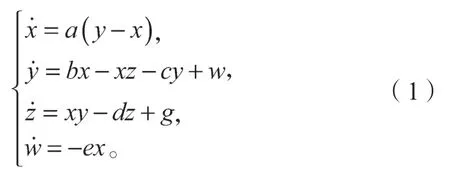
式中：a、b、c、d、e、g均為實數，且a、b、c、d、e均為正實數，e為控制參數。

由式（1）可知，該混沌系統是基于狀態變量反饋控制實現的超混沌系統。

當系統（1）取a=35、b=35、c=1、d=3、e=3、g=-27時，得到該超混沌系統的相軌跡圖如圖1所示。

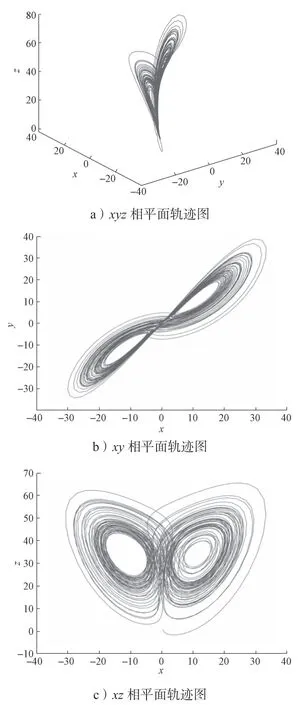
圖1 超混沌系統（1）的相軌跡圖Fig.1 Phase diagram of the hyperchaotic system (1)

通過觀察圖1所示超混沌系統的相軌跡圖可以得知，該超混沌系統的渦卷數目為2個，有明顯的混沌現象。

3 超混沌系統的動力學分析及數值仿真分析

3.1 超混沌系統的動力學分析

由于非線性混沌系統的解析解通常無法輕易獲得，所以需要通過平衡點穩定性分析、耗散性分析等定性分析的方法獲得系統的近似形態。

3.1.1 平衡點穩定性分析

對于一個四階非線性自治系統，經平衡點線性化后得到其雅可比矩陣，根據解得的特征值性質的不同，會得到不同性質的平衡點。下面針對每一個平衡點逐一展開討論。

令系統（1）的右邊全部等于0，則可以得到如下方程組：

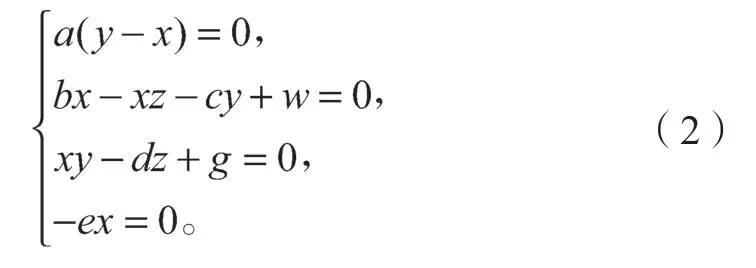
解得系統（1）的平衡點有兩種情況：

1）d=0時，系統無平衡點；

2）d≠0時，系統存在平衡點P1（0, 0,, 0）。

3.1.1.1 系統（1）無平衡點時的超混沌吸引子

取a=8、b=0.1、c=1、d=0、e=2、g=-8時，初值為[0 1 1 0]時，系統（1）沒有平衡點，且此時該新超混沌系統的Lyapunov指數為：

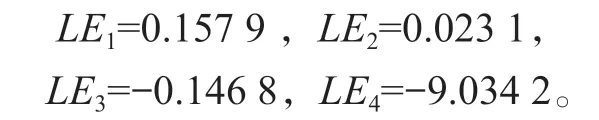
可見，系統（1）滿足存在兩個正的Lyapunov指數的條件，故該系統存在隱藏的超混沌吸引子，其相圖如圖2所示。

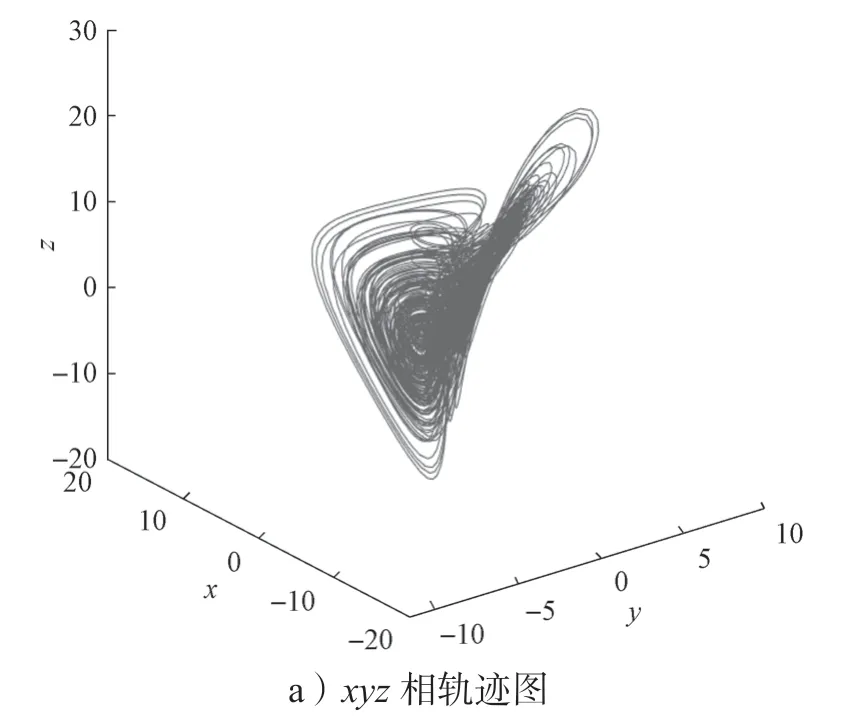
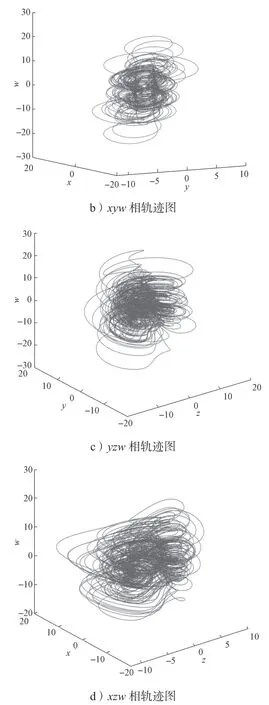
圖2 系統（1）隱藏超混沌吸引子的相軌跡圖Fig.2 Phase diagram of the hidden hyperchaotic attractor of system (1)

通過觀察圖2所示的相軌跡圖可知，該系統有明顯的混沌現象。

3.1.1.2 系統（1）有一個平衡點時的超混沌吸引子

當d≠0時，系統存在平衡點P1(0, 0,, 0)。其中，g可取任意實數，則該系統有無限平衡點集。在平衡點處做線性化處理，可得到系統（1）線性化后的雅可比矩陣為

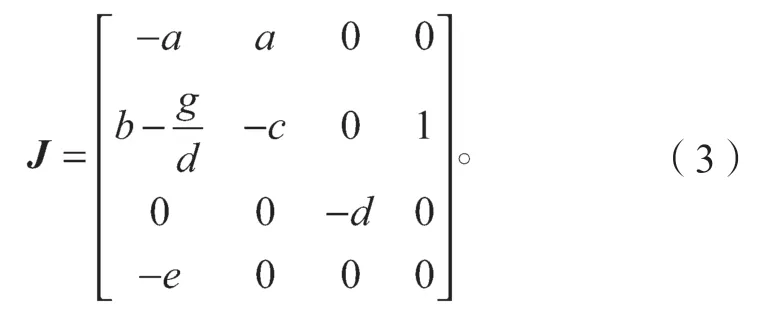
將式（3）代入平衡點坐標后，令|λI-J|=0，則系統（1）在平衡點處線性化后得到的特征方程為

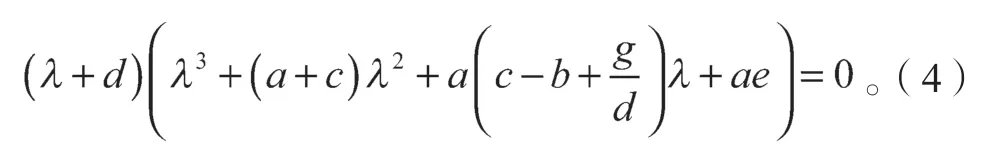
特征方程的第一個特征值為λ1=-d，設

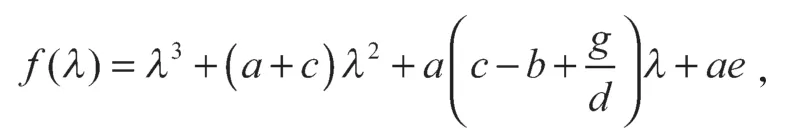
則根據Routh-Hurwitz判據，可得：

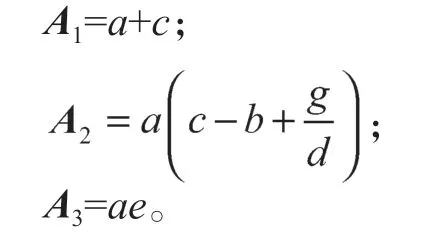
則有

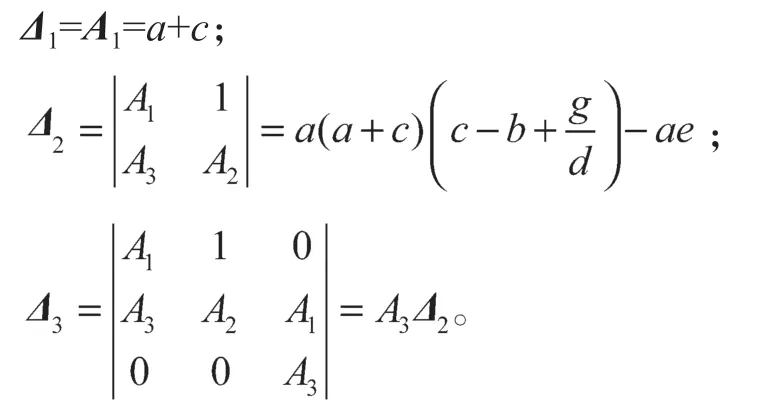
若系統（1）同時滿足

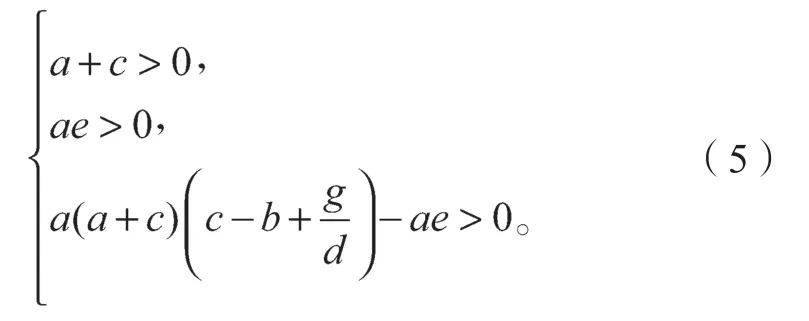
當系統（1）取a=35、b=35、c=1、d=3、e=3、g=-27時，在平衡點P1處對系統（1）進行線性化處理后，求得對應特征方程（4）的解為

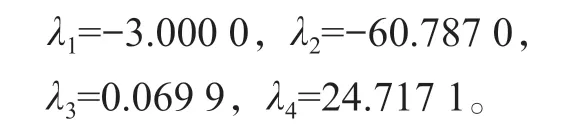
此時，特征方程（4）的解為兩正兩負的實特征值，且所有特征值之和滿足λ1+λ2+λ3+λ4<0，故此時系統（1）的平衡點P1是具有二維穩定流形和二維不穩定流形的鞍焦平衡點。將此時系統（1）的各參數取值代入后，式子仍然成立，故P1是不穩定的鞍焦點，系統呈現超混沌現象，此時系統（1）的相圖如圖3所示，可見結果符合前文論述結論。

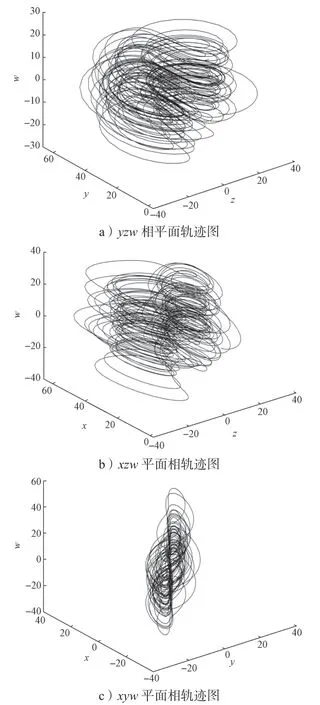
圖3 系統（1）有一個平衡點時的超混沌吸引子相軌跡圖Fig.3 Phase diagram of the Hyperchaotic system (1)with an equilibrium point

3.1.2 對稱性分析

對于超混沌系統（1）做(x,y,z,w)～ (-x, -y, -z,-w)變換后，發現該系統的狀態方程仍保持不變。故該系統關于z軸對稱，且這種對稱關系對于系統的所有參數都成立。

3.1.3 耗散性分析

系統（1）的相空間容積率為

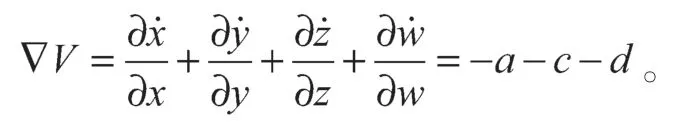
當a-c-d<0時，系統是耗散的，相空間的體積元將以指數形式收斂：

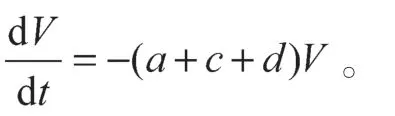
解得V=V0e-(a+c+d)t。

即當時間趨近于無窮大時，系統的每一條軌線都將以-(a+c+d)的速度指數收斂至0。最終，系統的所有軌線收斂至體積為0的集合，系統的所有軌線都固定于一個吸引子上。

當系統（1）取a=35、b=35、c=1、d=3、e=3、g=-27時，=-(35+1+3)=-39<0，即此時的系統（1）是耗散的。

3.2 超混沌系統的數值仿真分析

由于混沌系統的解對初值具有敏感依賴性，從而很難證明所獲得的近似解是否會收斂于系統的真實解。因此，除了對系統進行定性分析之外，還需要通過數值分析方法，如Lyapunov指數譜、Poincaré圖等，對混沌系統進行進一步的定量分析，以彌補定性分析的某些不足，從而更全面地研究動力學系統的混沌特征。

3.2.1 Lyapunov指數譜及維數

當取a=35、b=35、c=1、d=3、e=3、g=-27時，可以計算得：

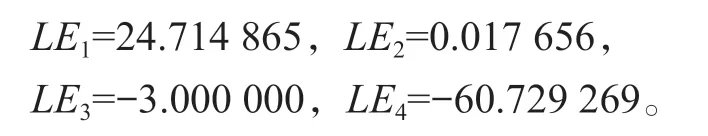
此時，系統（1）滿足存在兩個正的Lyapunov指數，處于超混沌狀態，其Lyapunov指數圖見圖4。

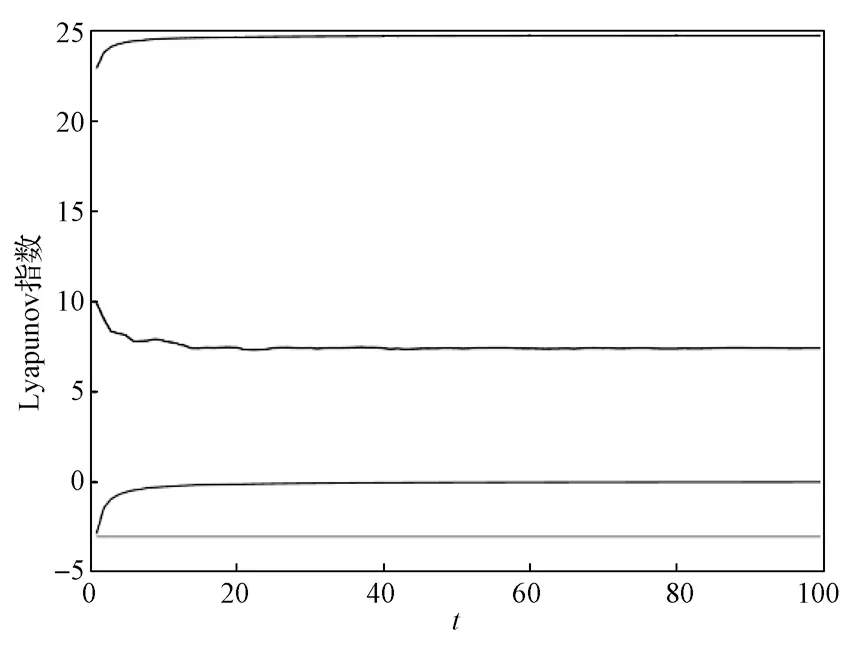
圖4 系統（1）的Lyapunov指數圖Fig.4 Lyapunov exponential diagram of system (1)

Lyapunov維數計算公式為

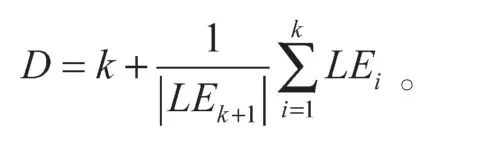
其中，k滿足以下條件：

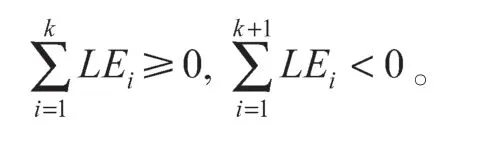
將Lyapunov指數代入后算得，

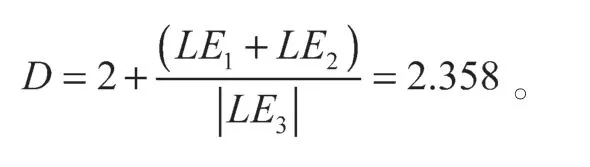
故可知該超混沌系統為分數維，具有豐富的動力學特性。

3.2.2 Poincaré截面圖

當選取參數a=35、b=35、c=1、d=3、e=3、g=-27時，繪制出該系統的Poincaré截面圖，如圖5所示。

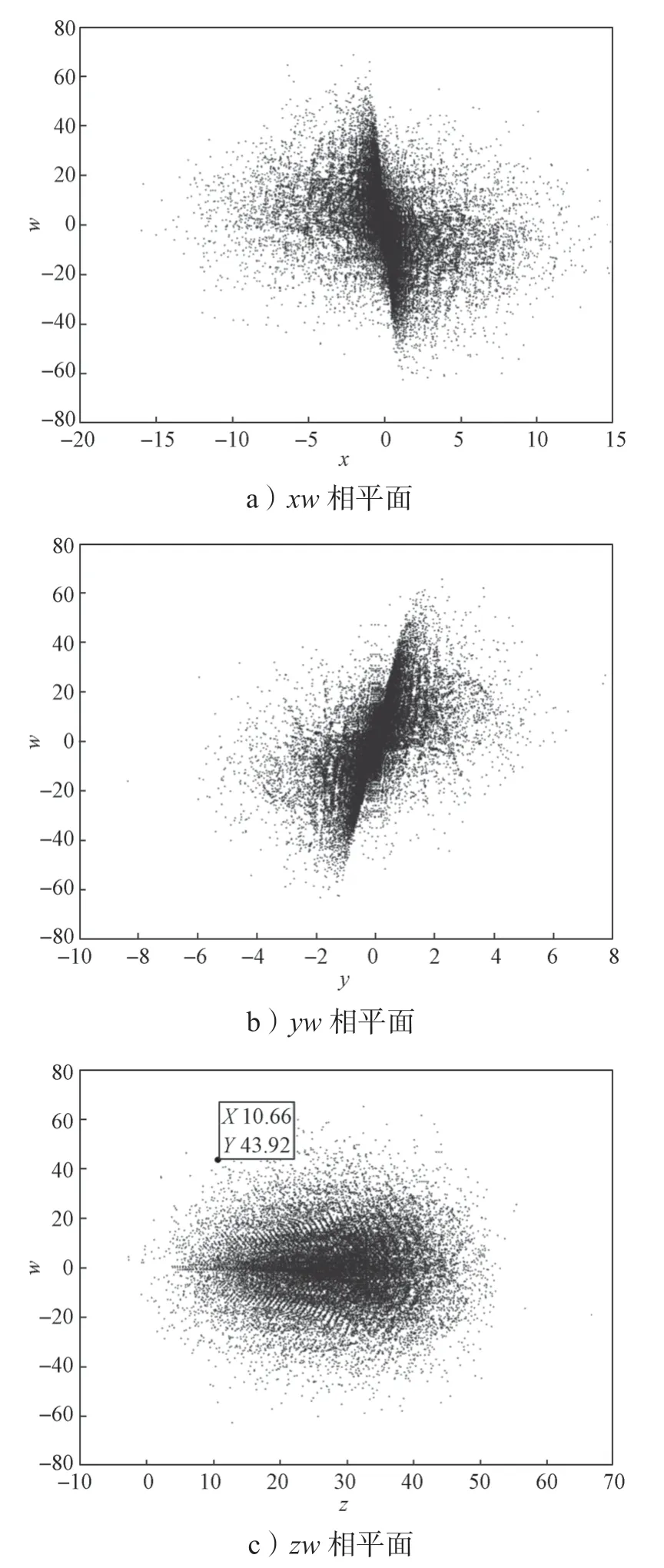
圖5 系統（1）的Poincaré截面圖Fig.5 Poincaré diagram of system (1)

觀察圖5所示的系統（1）Poincaré截面圖可以發現，不論是yz相平面還是xw相平面的Poincaré截面圖，上面都有著一片密密麻麻雜亂分布的點，結合該系統有兩個正Lyapunov指數的特征，可以得知此時系統（1）處于超混沌狀態。

4 超混沌系統的電路實現

本文采取模塊化設計思路，運用簡單的電感、電容、運算放大器等元件實現電路的搭建。

由于要運用到反相器等運算放大電路，需先將方程組（1）改寫為

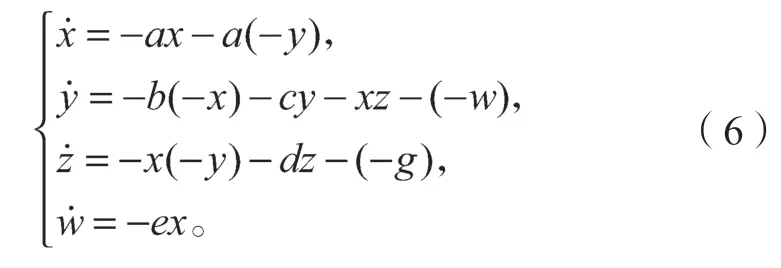
為了使信號在時域上擴展而幅度不發生變化，需要先對各變量取值范圍進行核查，若各變量取值超過元件額定值，則需要對系統的狀態方程進行時間尺度變換：

令τ=τ0，其中τ0是時間尺度變換因子，取τ0=100 μs，則方程組可改寫為

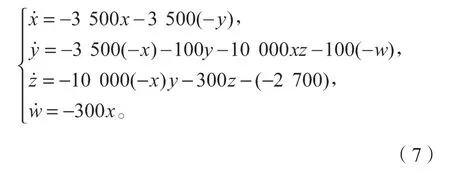
根據式（7），可搭建出其對應的輸出為x、y、z、w的電路圖，如圖6所示。

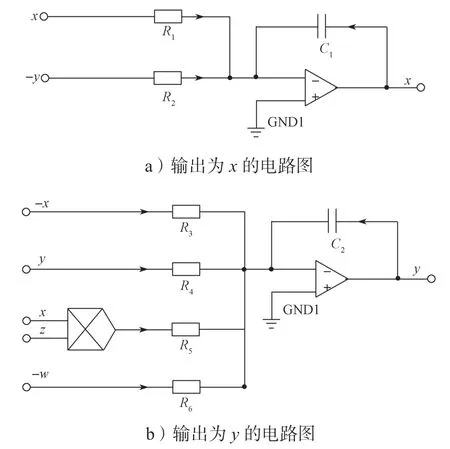
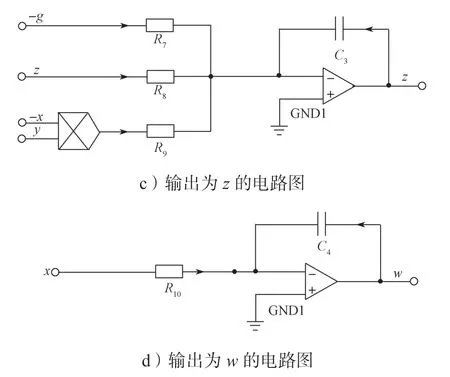
圖6 系統（1）的Simulink電路圖Fig.6 Simulink simulation circuit of system (1)

圖6中，當運算放大器工作于線性狀態時，其兩個輸入端可視為等電位。由于運算放大器的差模輸入電阻較大，故流入運算放大器輸入端的電流可以小到忽略不計，即可以將運算放大器的兩個輸入端視作開路，得到：

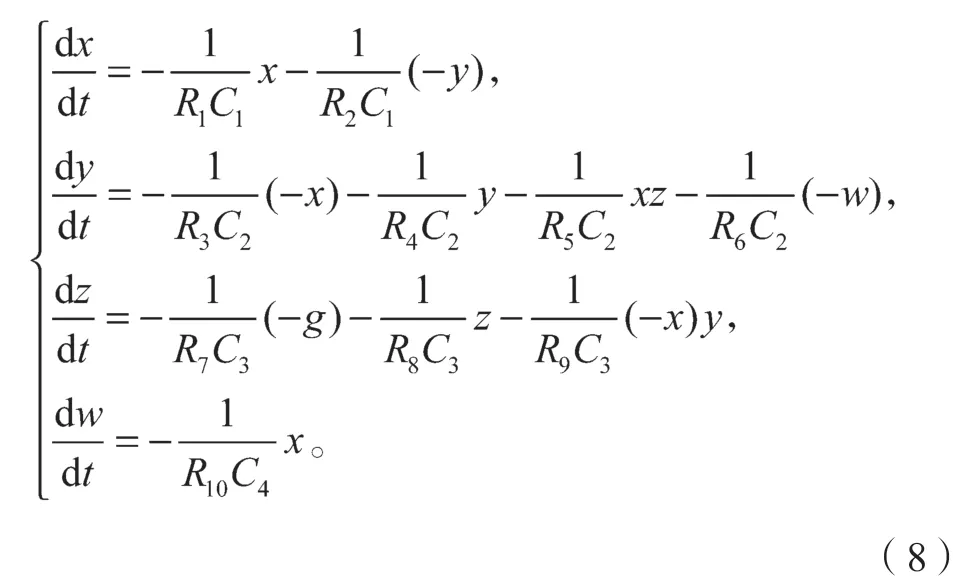
圖中的電容是為了避免因參數選取過大導致進入混沌前時間過長，特選取C1=C2=C3=C4=100 nF，比較式（7）和（8），可得：

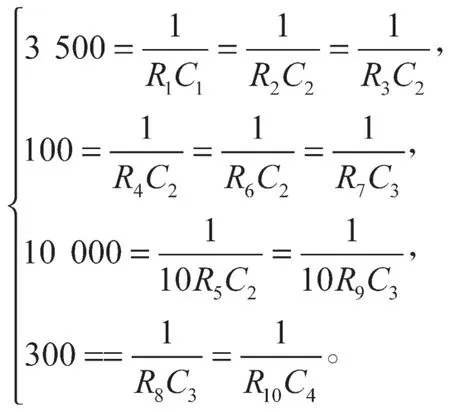
解得：R1=R2=R3=2.86 kΩ，

R4=R6=R7=100 kΩ，

R5=R9=0.1 kΩ，

R8=R10=33.33 kΩ。

故可得系統（1）的電路圖如圖7所示。

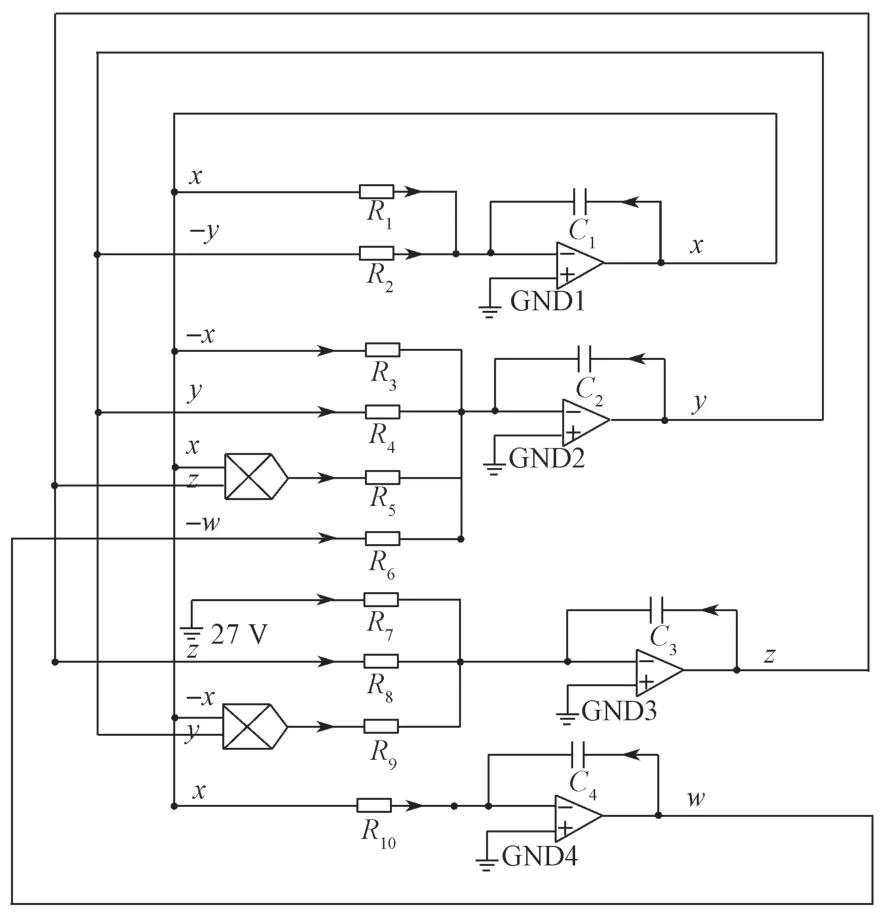
圖7 系統（1）的電路圖Fig.7 Circuit realization diagram of system (1)

5 超混沌系統電路的仿真驗證

為了證明設計電路的正確性，在Simulink中搭建了對應的模擬電路。本文采用了模塊化設計的思路，運用運算放大器、電容、電感等基本元件組成反相器，與積分器一起搭建出模擬電路。其中，給定運算放大器的門限電壓設置為±15 V，考慮到乘法器AD633JN的乘法因子為0.1/V，R5、R9的取值變更為1 kΩ，并按照計算出的參數設置元件的值，觀察示波器輸出的結果，所得仿真結果如圖8所示。

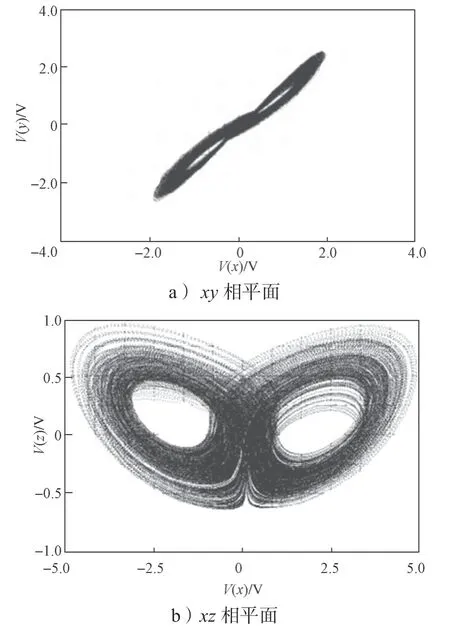
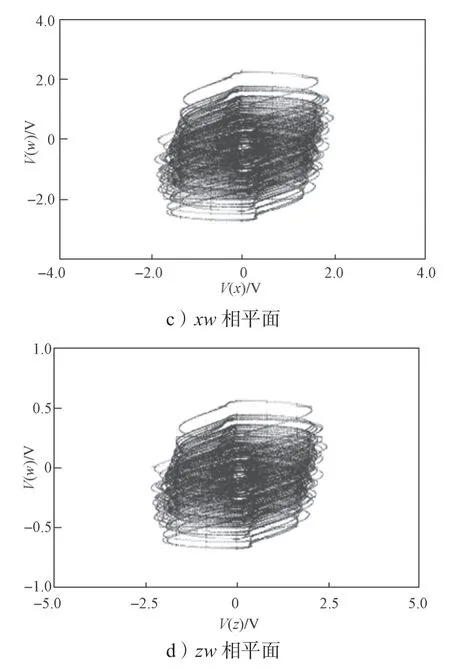
圖8 系統（1）的Simulink仿真結果圖Fig.8 Simulation diagrams of system (1)

將圖8所示仿真結果與吸引子相軌跡圖進行對比，發現該超混沌電路的實驗結果與Matlab的數值仿真結果一致，這證明所設計的電路準確有效。

6 結語

相比于常見的三維混沌系統，超混沌系統有著更為復雜的混沌特征，更能滿足現代通信保密、圖像加密、人工神經網絡、非線性電路等領域的需求。如何找到結構簡單、動力學特性豐富的超混沌系統，并且將其應用到實際生產與生活中，是混沌理論一直追求的目標。

本文采用狀態變量反饋法構造了一個新的超混沌系統，通過根據平衡點對應的雅可比矩陣計算出相應的特征值判定平衡點的穩定性等定性分析方法，以及計算Lyapunov指數和維數、繪制Poincaré截面圖等定量分析方法，對超混沌系統進行了基本的動力學分析。通過基本的運算放大電路，搭建了新超混沌系統的電路模型，并利用Matlab-Simulink仿真模塊庫驗證了電路實現的準確性，為超混沌系統的研究提供了新的思路。