城市道路混合路由算法研究
谷志茹,榮 青,李 敏,黎朝暉,信志平
(湖南工業大學 軌道交通學院,湖南 株洲 412007)
1 研究綜述
在新興的車聯網通信系統中,因車聯網拓撲結構的高速變換且復雜難測,使得各網絡節點信息分布不均勻,資源調配難以有效滿足不同環境下的通信需求[1]。因此有研究者提出在交叉路口和雙向快速4車道兩類交通場景下,對按需距離矢量路由(Ad hoc on demand distance vector routing,AODV)和目的節點序列矢量路由(destination sequenced distance vector routing,DSDV)進行性能比較[2],結果表明不同路由算法對不同場景的表現性和適應性均不同。故本研究選取城市道路上復雜多變的交通路口作為研究場景,在此場景下,因路邊單元實時與過往車輛進行信息交互,交通燈覆蓋的通信區域內可能會出現車輛密度突變而導致的車聯網系統信息冗余和數據丟失等問題。本文擬對車車通信時所涉及的路由算法進行綜合研究。
已有研究中,所涉及的基于地理位置的路由算法大多采用貪婪周邊無狀態路由(greedy perimeter stateless routing,GPSR)[3]的轉發思想,且總是選擇離目的地最近的節點轉發,以減少路徑消耗,但對節點位置信息要求極高,且易陷入路由空洞。文獻[4]對其進行了優化,在選擇下一跳節點時,選傳遞范圍內最可靠的節點轉發,在高速、網絡密集的環境中,極大地減少了時延和節點跳數,提高了可靠率。但在低速、網絡稀疏的環境中,其性能不佳。文獻[5]利用人工蜂群算法尋找最小轉發路徑,避免陷入路由空洞。但若兩節點相距較遠,路徑規劃會增加計算復雜度和時延性能,這是因為雖避免了路由空洞,但節點跳數增多。文獻[6]在選擇下一跳節點時,綜合考察了兩節點間的節點接近率和下一跳節點前向轉發區域密度,以此作為評價指標,擇優選擇下一跳節點,避免多跳狀態信息造成的路由開銷。文獻[7]提出了路徑感知GPSR策略,即在節點陷入路由空洞時復制數據包,并同時使用左手和右手轉發規則,以繞過路由空洞。文獻[8]針對交叉路口環境下的數據轉發情形,在選擇下一跳節點時,兼顧鏈路穩定性和距離衰減性等因素,提前預測路口節點,使數據包能夠利用路口協調節點來投遞數據,避免了路由環路問題。
基于拓撲的路由算法采用按需距離矢量路由AODV[9]的轉發思想,節點通過廣播路由請求包和回復路由應答分組,建立路由通路。但網絡過于密集或稀疏都會影響通路的建立。針對這一問題,文獻[10-11]根據接收節點所處環境信息動態配置節點等待時延和轉發概率,再按優先級先后轉發,避免了局部網絡風暴和傳輸延遲等問題。
綜上可知,無論是基于地理位置還是基于拓撲的路由算法,在紅綠燈路口下的適應性和表現性都有所不足,如:
1)節點密度驟增時,貪婪轉發算法因周期性地進行鄰居列表訪問,信息更新過于頻繁,因而導致計算復雜,工作量增大;
2)節點密度驟減時,距離矢量轉發算法在高速移動的節點間無法建立穩定的路由通路,數據投遞準確率低且存在極大的傳輸時延。
針對以上算法在紅綠燈路口下實施時存在的弊端,提出一種自適應限制性混合路由算法(adaptive restrictive hybrid routing protocols,ARHP),對其進行優化:
1)對各節點數據投遞時的通信區域設置限制條件,并在受限區域內對節點密度、運動方向和速度進行考察,通過權重分析擇優選取下一跳節點。
2)針對不同的網絡環境設置不同的轉發模式,通過對當前網絡狀態進行實時評估,完成轉發模式間的切換。
2 ARHP路由算法的構成
2.1 受限貪婪轉發
基于地理位置的路由GPSR選擇下一跳節點時,僅通過判斷各節點間的歐氏距離,就盲目地投遞數據包,極易陷入路由空洞。針對這一問題,提出從多方面考察鏈路質量,對其進行綜合評價,以此擇優選取下一跳節點,其中可考察的因素為通信范圍內的有效鄰居節點數和兩通信節點間的鏈路生存時間。
2.1.1 有效鄰居節點數
在選擇下一跳節點時,需考慮通信范圍內的鄰居節點數量,可對節點的通信范圍進行限制。鄰居節點通信區域內的受限節點數量如圖1所示。
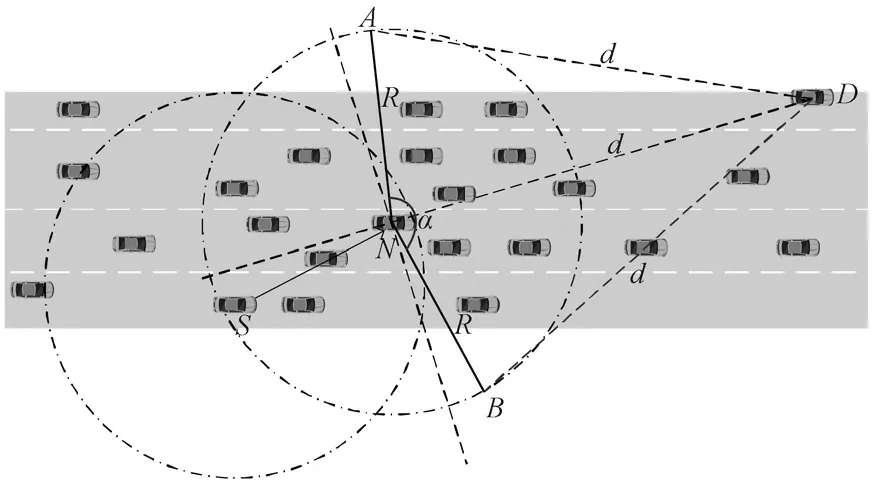
圖1 鄰居節點通信區域內的受限節點數量Fig.1 Number of restricted nodes in communication region of neighbor nodes
由圖1可知,將所考察的下一跳節點與目的節點相連接,以考察的下一跳節點為原點,最大通信距離R為半徑,畫一個圓,在圓上所有與目的節點間距離短于原點到目的節點間距離的節點均納入原點的鄰居節點考察范圍。即在考察范圍內的節點均需位于平面角度為α的扇形區域內,且滿足
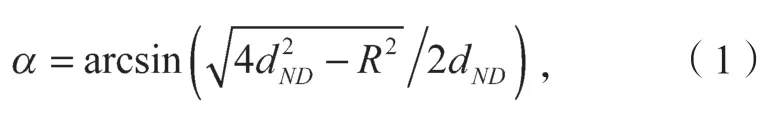
式中:R為節點的最大通信半徑;dND為鄰居節點N(xN,yN)到目的節點D(xD,yD)的距離,其值可由式(2)得到。
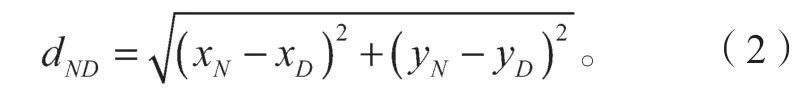
若已知鄰居節點通信范圍內的任意節點i的坐標為i(xi,yi),可求出節點i到目的節點D的距離:
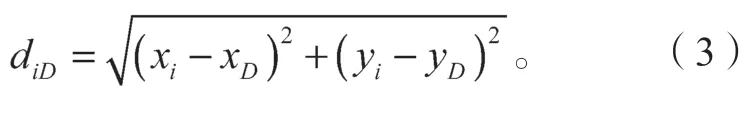
結合式(2)和式(3),可求得任意節點i對應的距離函數fi。
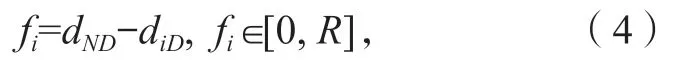
式中fi的有效取值范圍為[0,R],若任意節點i的距離函數不在此區間,則視該節點為無效節點。
設隨節點有效性變化的因變量為K,當任意節點i同時滿足公式(1)和(4)時,K>0,有效鄰居節點數量為n+1;反之,K≤0,節點不計數。故有效節點密度(effect node density,DEN) 如下:
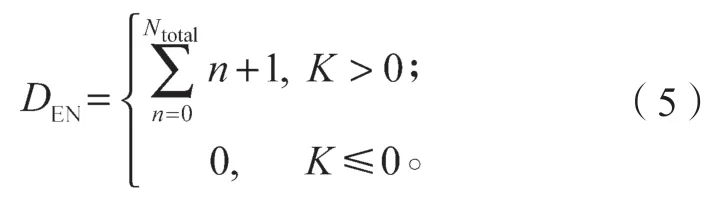
式中:n為通信范圍內有效鄰居節點的數量,初值為0;Ntotal為通信范圍內所有節點數量。
2.1.2 鏈路生存時間
假若源節點S和鄰居節點N在現階段相互保持著鏈路通信,經過一段時間后,兩節點的相對位置發生偏移,鏈路斷裂。這段時間即為兩節點的鏈路生存時間,可由源節點S和鄰居節點N的位置、速度聯立求解獲得。
已知S(xS,yS)為源節點,N(xN,yN)為鄰居節點;根據坐標信息可求得節點S、N間的平面夾角θ和歐氏距離dSN:

當兩節點同向移動時,將式(6)(7)代入式(8)中,則可求出節點S、N間的最大鏈路生存時間TLink。
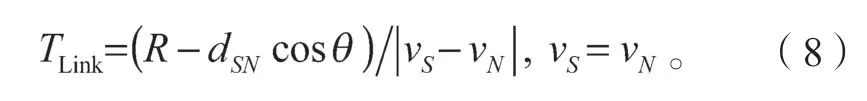
式中:vS為源節點S的移動速度;vN為鄰居節點N的移動速度,vS=vN表示兩節點同向;當間距dSN一定時,角度越大,鏈路生存時間TLink越長。
同理,當兩節點反向移動時,根據兩節點的相對位置,即可求出節點S、N間的TLink。
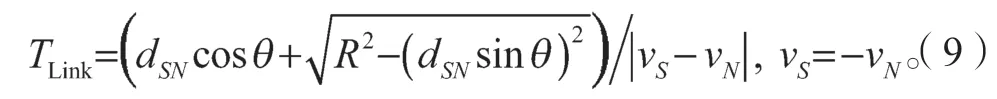
式中:vS=-vN表示兩節點反向;當間距dSN一定時,角度越大,鏈路生存時間TLink越短。
當兩節點反向移動時,若要計算鏈路生存時間,需提前考察式(10)是否成立。
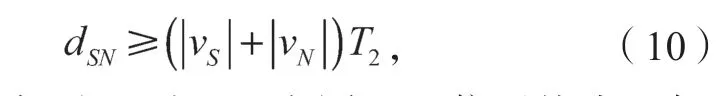
式中,T2為數據處理時延,在同一通信系統中,任意兩節點間的數據處理時延近似相同。
在數據傳輸期間,源節點S和鄰居節點N的相對位置發生變化,其變化示意圖如圖2所示。
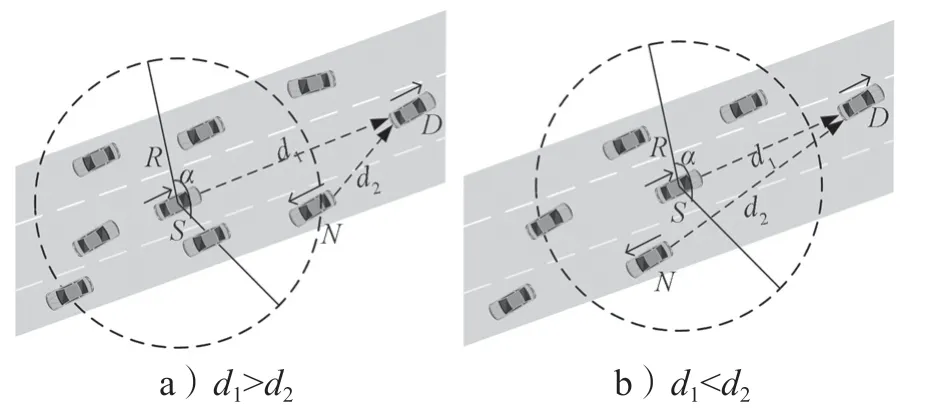
圖2 經T2后,兩節點相對位置變化情況示意圖Fig.2 Changes of the relative positions of two nodes after T2
在圖2a中,經過時間T2后,源節點與目的節點間距離d1大于鄰居節點與目的節點間距離d2,即d1>d2時,可將鄰居節點N納入可選節點,并將其與源節點S間的鏈路維持時間TLink×1。
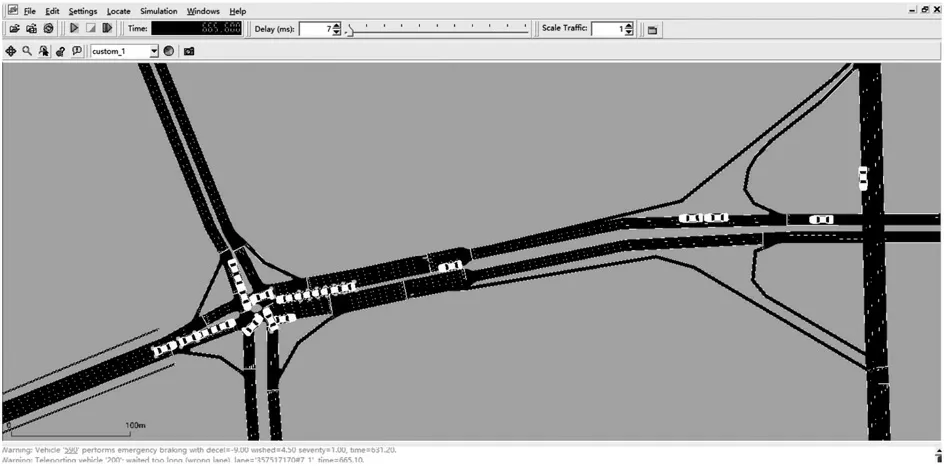
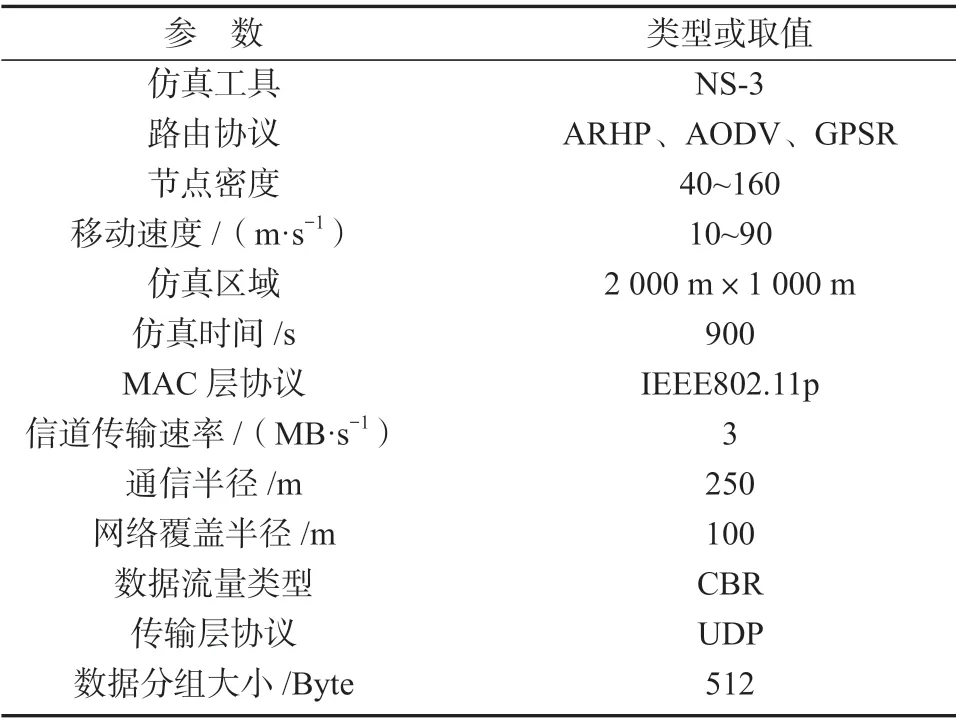
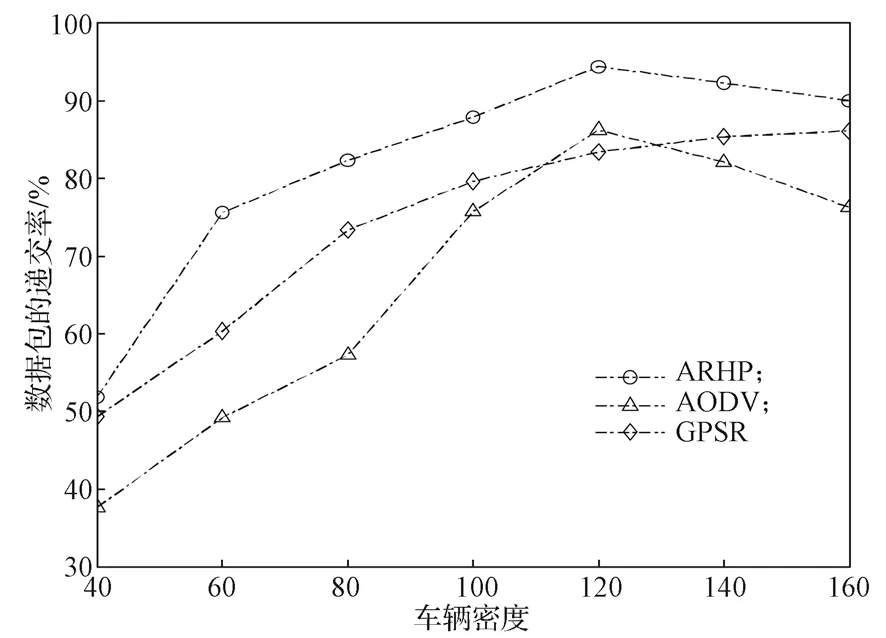
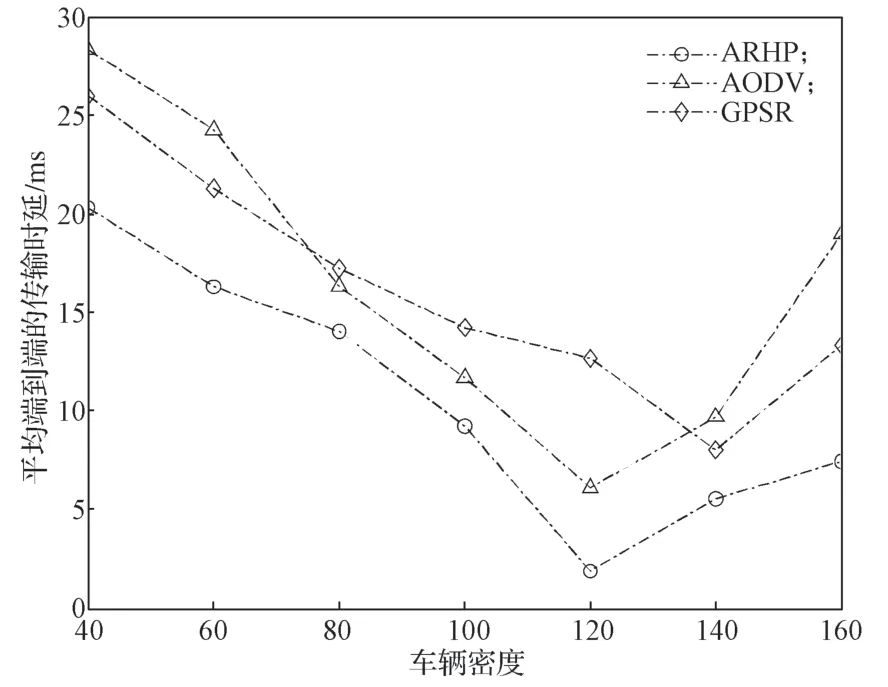
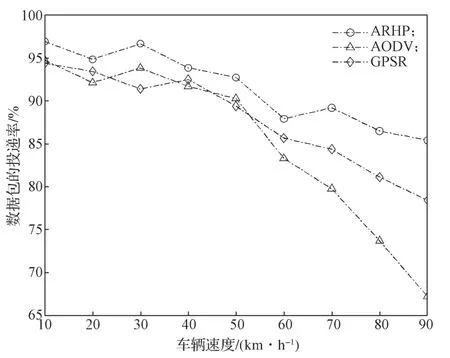
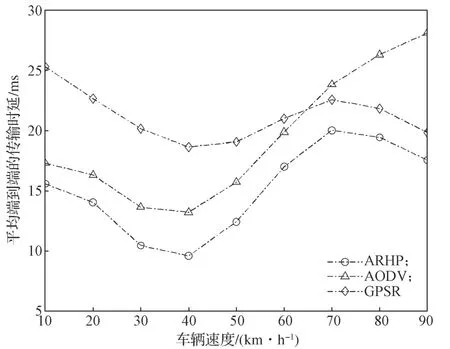
圖2b中,經過時間T2后,d1 設隨數據交互后節點間位置變化而變化的考察變量為Q,經過時間T2后,若d1>d2,則Q>0,鏈路維持時間為TLink×1;反之,若d1 綜合考慮鏈路生存時間和有效鄰居節點密度,對它們進行層次權重決策分析,并建立鏈路質量的相關權重函數Lquality。 式 中:w1、w2為權重值,且w1+w2=1,0 通過以上的優化改進,數據包可在限制性條件下高效投遞。但在網絡密集處,受限貪婪轉發因缺乏一個已建立的穩定路由,導致每個節點每一次數據投遞都要對鄰居節點集進行計算,計算負載大。因此,提出距離矢量轉發機制探知數據投遞路徑,按需建立穩定路由,針對交通擁堵、車輛密集的場景,提前做好線路規劃。 由于距離矢量轉發能高效傳遞數據信息的前提是建立穩定路由。故可對當前網絡狀態進行實時評估,以評估值作為兩種轉發模式間的切換依據。其中常用的評估指標有:節點位置偏移、鄰居節點數量變化率。 2.2.1 節點位置偏移 分別設當前節點S和其任意鄰居節點i在t-1時刻的位置坐標為、,目的節點的位置坐標為D(xD,yD),可得出節點S與目的節點D間的平面夾角,為 任意鄰居節點i與目的節點D間的平面夾角可表示為 同時,可求出在t-1時刻,節點S和節點i的間隔距離,為 已知當前節點S的移動速度為vS,可預測出該節點在下一時刻t相對于目的節點的偏移位置[12]: 同理,已知任意鄰居節點i的移動速度vi,可預測出該節點在下一時刻t相對于目的節點的偏移位置,為。 由式(15)和式(16),再聯立鄰居節點的偏移位置it求解,可得出t時刻節點S和節點i的間隔距離,為 由式(14)(17),可以得出當前節點的所有鄰居節點位置總偏移(node position migrate,NPM)量dNPM,為 已知當前節點的所有鄰居節點中移動速度最快和最慢的節點的速度為vmax、vmin;在t-1時刻到t時刻間,它們對應的最大位移量分別為S1、S2, 分析式(18)~(20)可知,當節點位置總偏移量dNPM≥S1時,視為動態網絡;而當dNPM≤S2時,則視為通信區域內的節點處于相對靜態狀態。 2.2.2 節點數量變化率 節點數量變化率為當前節點在t-1時刻的鄰居節點數Nt-1和t時刻的鄰居節點數Nt差值的絕對值與Nt之比,即節點數量變化(change number,CN)率ηCN為 其中,Nt>0。當ηCN趨于0時,可認為通信范圍內節點數量不變,網絡連通性良好。 綜合考察節點位置偏移和鄰居節點數量變化率,對它們進行層次分析以判斷當前網絡狀態(network status,NS),用VNS表示,為 式(22)中,ρ1、ρ2均為權重值,且ρ1+ρ2=1,0<ρ1<1, 0<ρ2<1。當VNS≥max{dNPM,ηCN}時,狀態標志位Flag=1,采用受限貪婪轉發。當VNS趨于0時,網絡狀態標志位Flag≠1,切換至受限距離矢量轉發模式。 在交叉路口的網絡通信環境下,設計車與車之間的網絡布局和數據交互方式,其中所涉及的ARHP路由算法的具體實現過程如下。 step 1對當前節點通信范圍內所有鄰居節點進行鏈路質量權重值計算,根據所求Lquality值判斷該節點是否參與競爭轉發; step 2若Lquality≤0,則不參與競爭。當所有鄰居節點的Lquality值皆小于0時,當前節點暫存數據包,并不斷訪問鄰居列表直至耗盡數據包的生存期; step 3若Lquality>0,該節點參與競爭轉發,將Lquality反饋回當前節點,對其所處網絡狀態VNS進行實時評估。 step 4當網絡狀態標志位Flag=1,采用受限貪婪轉發進行數據投遞。即當前節點將各鄰居節點反饋回的Lquality值從高到低依次排列,擇優選取權重值最大的節點進行投遞; step 5當網絡狀態標志位Flag≠1時,轉發模式切換為距離矢量轉發;即節點僅向平面角度為α的區域內的鄰居節點不斷地廣播路由請求包,以建立路由通路,使此后的數據可直接在此通路投遞,無需進行額外計算。 在整個數據傳輸過程中,需時刻對當前網絡狀態VNS進行判斷,一旦達切換閥值即切換轉發模式。也需實時判斷當前節點是否為目的節點,若為目的節點,說明數據已傳輸成功,退出當前通信網絡;反之,重復以上傳輸過程,直至數據投遞完成。 實驗采用開源網絡仿真平臺NS-3仿真網絡算法,以交通模擬器SUMO(simulation of urban mobility)模擬車輛在遇到紅燈或綠燈時的運動軌跡。對ARHP進行不同環境下的實驗仿真,并分析對比ARHP、AODV和GPSR多種路由協議在數據包的遞交率和端到端時延上的性能表現。 在OpenStreetMap官網上導出湖南省株洲市天元區的地圖。利用SUMO的工具插件對其進行處理,獲得道路環境信息,選取模擬區域2 000 m×1 000 m,10個紅綠燈路口、15條雙向兩車道的道路交通模型。車輛的初始位置是隨機分布的,車輛在道路上的運動受車輛沿道路跟隨模型(Kraus模型)的限制。且每輛車都配備了全向天線和GPS定位器,可獲取車身的位置、行駛方向、運動速率等信息,并實時與其他車輛節點共享。任意選定其中一個紅綠燈十字路口,其仿真道路場景如圖3所示。 圖3 仿真道路場景圖Fig.3 Road simulation scene 圖3中,車輛隨機進入等待紅綠燈行列,進入的車輛數取值范圍為[40,160]。假設車輛在綠燈場景下均勻速行駛,其取值范圍為[10,90] km/h,仿真場景參數見表1。 表1 仿真場景參數Table 1 Simulation scene parameters 設計兩組實驗,一組實驗設置固定車速為v=60 km/h,令節點密度為[40, 160],步長為20;另一組實驗設置固定節點密度n=120,車速變化范圍為[10,90] km/h,步長為10。進行多次實驗取其均值,分析各算法在不同節點密度和車輛速度下的性能表現。仿真時所采用的性能指標定義如下。 1)包的遞交率。指目的節點接收的包總數Nreceive與源節點發送的包總數Nsend的比值,它反映了網絡數據傳輸的成功率(packet delivery rate,PDR),符號為rPDR,即。 2)平均端到端時延(average end-to-end delay,AEED)。指將所有數據包接收和發送之間的時間差ti求和并取均值,其反映了網絡數據傳輸效率,符號為AEED,即。 為了評估節點密度對系統通信性能的影響,實驗一對ARHP、AODV和GPSR在數據包的遞交率、平均端到端的時延等方面的性能表現進行仿真分析,取其均值構成關聯曲線圖,實驗結果見圖4和5。 圖4 不同節點密度下的數據包遞交率變化曲線Fig.4 Change curve of packet delivery rate under different node densities 由圖4所示不同節點密度下的數據包遞交率的對比結果可知,隨著節點密度的增大,路由環境趨于穩定,GPSR和AODV的遞交率持續穩步增長,在節點密度從n=80到n=120間時,AODV因所需的穩定網絡結構完全搭建好,遞交率快速增長了29%;而后因出現局部廣播風暴,遞交率有所下降。ARHP在節點密度小時,無法建立牢固的路由通路,故采用受限貪婪轉發在扇形區域α內做最優數據投遞路徑選擇;隨著節點密度增大到n=120時,采用有限貪婪轉發和距離向量混合轉發模式,數據包遞交率達最優值;然后完全采用受限距離向量轉發模式,若節點密度持續增大,數據包的投遞率因受環境因素的影響而有所降低。但ARHP投遞率仍平均比AODV和GPSR分別高16%, 8%以上,體現了ARHP選擇下一跳節點時,根據受限條件和所處通信環境,采用了最有利的轉發模式。 由圖5所示不同車輛密度下端到端的傳輸時延大小可知,節點為n=40時,網絡連通性較低,易陷入路由空洞和造成數據丟失,端到端的時延值均較高。節點數在80到120間時,ARHP的端到端時延大幅度下降,降到1.8 ms,因節點密度增加,路由通路已建好,下一跳節點選擇時無需實時進行參數計算便可維持高效的距離向量轉發。當n>120后,網絡出現局部密集,路由通路的建立和節點間數據交互所需的時延增大,ARHP的傳輸性能下降,但結果顯示ARHP較AODV、GPSR數據傳遞造成的端到端時延仍低6%以上。 圖5 不同節點密度下平均端到端傳輸時延曲線Fig.5 Transmission delay curve of average end-to-end delay under different node densities 為評估不同車速對通信系統性能的影響,實驗二對ARHP、AODV和GPSR在不同車速下的各方面性能表現進行了數據分析,實驗結果見圖6和7。 圖6 不同車輛速度下數據包遞交率變化曲線Fig.6 Variation curve of packet delivery rate under different vehicle speeds 圖6為不同車速下的數據包投遞率對比結果。由圖可知,車速較低時,網絡連通性好,三者的投遞率均有較好的性能表現。隨著車速增大,投遞率均逐漸降低,當車速大于v=60 km/h時,網絡拓撲結構高速變換,許多路由通路斷裂,數據包大量丟失或傳輸錯誤,GPSR和AODV的投遞率分別急速下降了7.3%和16%。ARHP因進行了高效的數據投遞,且根據環境自適應的調整信標間隔周期,快速地適應車速變換帶來的鄰居列表更新頻率,高效組網構建路由通路,極大地減緩了投遞率的下降速度,性能表現優于AODV和GPSR。 圖7為3種路由協議在不同車輛速度下平均端到端的時延。由圖可知,車速較低時,路由通路穩定,GPSR因需對鄰居節點進行周期性參數計算,端到端的時延偏高。隨著車速增大,鏈路連通性降低,AODV無法建立穩固的路由通路,需反復進行路由訪問,因而增加了節點跳數和傳輸時延;GPSR和ARHP因其路由傳輸特點,受到速度變化的影響相對較小,故兩者的傳輸時延均低于AODV。 圖7 不同車輛速度下平均端傳輸到端時延變化曲線Fig.7 Variation curve of average end-to-end transmission delay under different vehicle speeds 本文提出一種基于貪婪轉發和距離向量轉發的快速組網混合路由算法ARHP,解決了城市道路紅綠燈路口場景下,車輛密度突變給通信系統帶來的信息冗余和數據丟失等問題。ARHP算法結合了貪婪轉發對鄰域節點選擇的高效性和距離矢量轉發對降低計算復雜量的優化性。在貪婪轉發中,對鏈路質量和端到端時延值綜合考察,對鄰域節點進行最優選擇,網絡密集時切換至距離向量轉發模式,減少不必要的計算量,這樣可以有效緩解網絡負載過重問題,節約數據傳輸開銷。對ARHP、AODV、GPSR 3種路由算法進行數據分析,大量的實驗仿真結果表明,隨著節點密度和移動速度的增大,ARHP算法在多方面的性能均優于AODV、GPSR路由算法。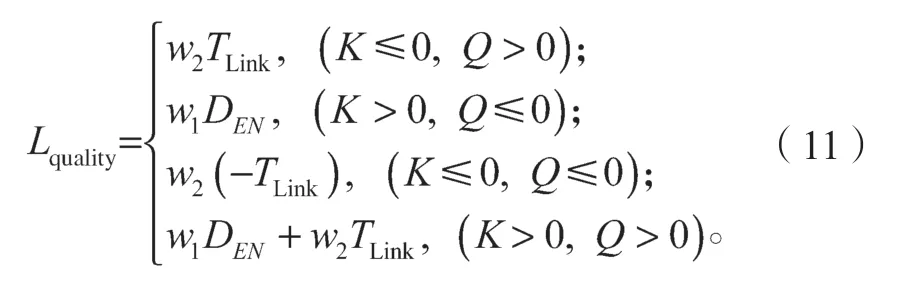
2.2 網絡狀態評估
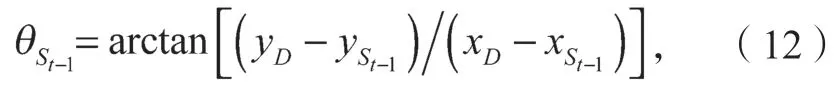
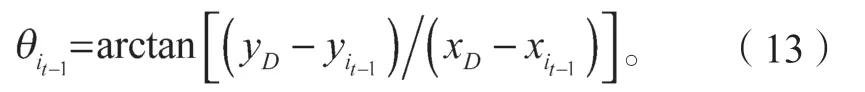
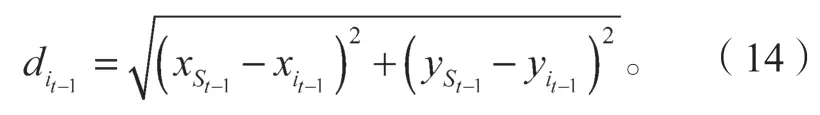
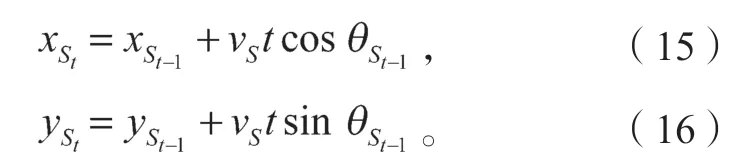
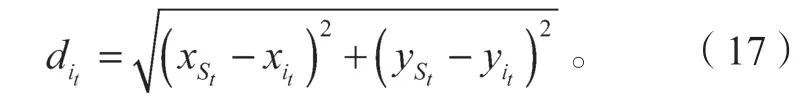
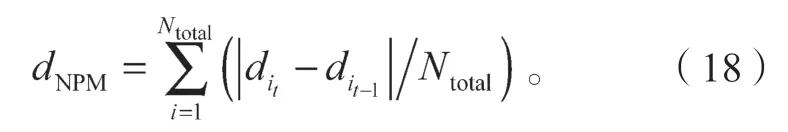

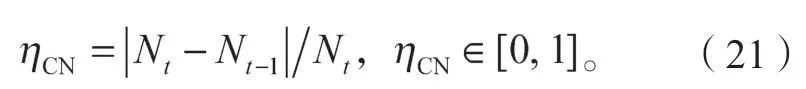

2.3 具體實現過程
3 仿真分析
3.1 場景設置
3.2 結果分析
4 結語

