數控機床加工精度誤差預測研究
柳 博,王文濤,彭才華
(蘭州現代職業學院理工分院,甘肅 蘭州 730000)
目前由于五軸數控機床在加工技術上的優越性能使其備受公眾關注,其無論在零部件的加工質量、生產效率等方面均遠遠高于三軸數控機床。但是在機械零部件的加工精度上較難控制[1]。本文基于此,對當下有關五軸數控機床提高精度的熱點問題進行研究,在其相比于三軸數控機床的各項優點上,采用定量等精度分析手段對五軸機床進行相應測試研究,以此顯著延長五軸數控機床的精度壽命提供一定的技術參考。
1 五軸機床的運動誤差
本次主要對五軸數控機床的運動誤差進行研究,其結構圖詳見圖1。首先需要對五軸數控機床的誤差進行逐個檢索剖析,其主要包括有兩根在X、Z方向上的旋轉軸線以及三根在X、Y、Z方向上的直線軸線[2]。國內部分專家對該數控機床的運動誤差做出了一定探討,研究表明該數控機床的旋轉軸誤差與直線軸誤差共計11種之多(其中包括3個直線軸運動誤差與8個旋轉軸運動誤差),這其中αay、βay、ray分別表示為A軸相對于X軸、Y軸、Z軸的旋轉角度誤差,而rxy、αyz、βzx分別為X軸、Y軸、Z軸的垂直角度誤差,詳見圖2所示。而且因為垂直角度誤差的測量與三軸數控機床的誤差測量方法大致相同,而且相比旋轉角度的運動誤差而言可以忽略不計,因此本文主要對上述八種旋轉角度誤差進行探討。
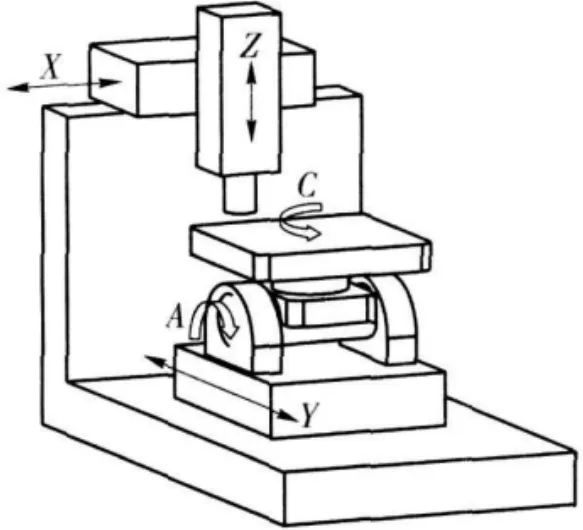
圖1 五軸數控機床結構簡圖
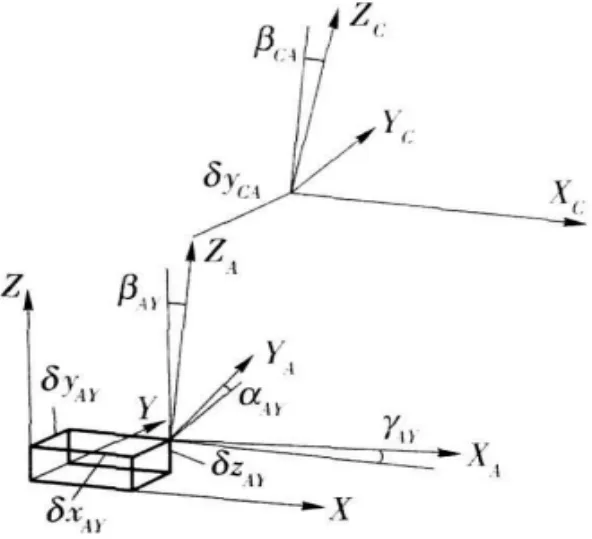
圖2 雙軸轉臺的運動誤差
2 運動誤差模型的建立
本模型主要采用變換矩陣數值分析法對五軸數控機床進行運行誤差建模分析,根據機床所對應的誤差與運動鏈可以得到機床的球桿儀球心的矩陣方程式:

由式中可見,Xtc、Ytc、Ztc為五軸數控機床中球桿儀球心的初始坐標測量值。但是由于其旋轉角度運動誤差均為微小量值,因此該齊次逆轉矩陣可以簡化如下:

基于本文所研究的五軸數控機床為雙旋轉工作機制,因此在該數控機床工作中可以采用多軸同步來進行加工任務操作,但是若同步的軸數過多將不利于對旋轉角度誤差的運動分解[3]。因此本文考慮較為便捷的運動設計方案,即使得C軸充分固定,讓A軸進行旋轉運動,而且也應該考慮到兩個球桿儀間的運動軌跡分別呈現切線方向、徑直方向、軸面方向三種軌跡狀態,從而產生了A軸旋轉球桿儀徑向、A軸旋轉球桿儀軸向、A軸旋轉球桿儀切向、C軸旋轉球桿儀徑向、C軸旋轉球桿儀軸向、C軸旋轉球桿儀切向六種軌跡姿態運動組合,因此可以得出球桿儀球心位置的向量矩陣(C軸固定,A軸旋轉):

依據建模計算得出:球桿儀兩端距離在特定位置的距離計算公式,且綜合所測球桿儀在特定的位置時的長度數值,可組合方程組,對方程組求解后即可得出誤差數值。
3 運動誤差分離
通過上述的誤差矩陣模型可知,其盡管可以通過齊次逆轉矩陣得出相應的矩陣方程式,但并不能得出精確的方程解,因此可以根據上述方程式的最優解推導出相應的精確方程解,但想求得最優解,就必須計算出旋轉角度誤差值,進而求解長度誤差[4]。通過上述的軌跡姿態運動組合進行相應操作,進而編寫相關程序使得五軸數控機床按照既定程序進行運動軌跡模擬,并且注意讀取工作臺中的球桿儀的各項長度測量值,實際的觀測值見表1。

表1 數控機床工作臺中的讀取長度值
五軸數控機床的旋轉角度運動誤差可以通過以下步驟解出:
當C軸固定但A軸旋轉時,工作臺上的雙球儀在A軸旋轉到90°時的讀數為LAA2,根據方程組LAA2=L-HβCAHrAY并代入βCA=L-LAA2-HrAY/H。當C軸固定但A軸旋轉時,工作臺上的雙球儀在A軸旋轉到0°時的讀數為LAA1,根據方程組LAA2=L-HβCA-HβAY并代入βCA=LLAA1HβAY/H。進一步由表1可知,當C軸固定時,球桿儀在旋轉軸A轉到0°和90°時的讀數分別為LCA1、LCA2,因此可以通過上述方程式中得出的機床工作臺各項誤差實際觀察值得到下列方程:
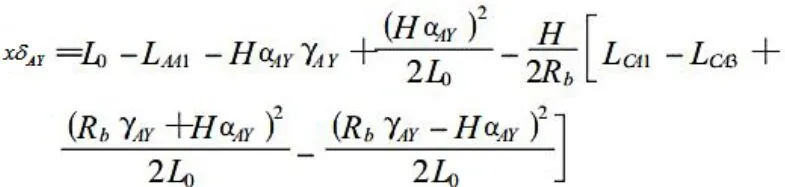
4 仿真
本次仿真主要應用Matlab軟件根據模型的向量矩陣進行誤差仿真模擬研究,首先精確的計算出五軸數控機床工作臺上的球桿儀在六種軌跡姿態上所處的實際長度值,并將其數值代入到上述的誤差分解步驟之中,進而求得誤差模型的識別誤差值。在本文的誤差仿真模擬過程中,設計該機床的球桿儀理想長度為120mm,A軸與C軸到機床工作臺球桿儀球心的理想距離分別為220mm、120mm,進而依據旋轉角度誤差的齊次矩陣模型得出相應的誤差值。通過表2可以看出,此誤差源的識別算法的可靠程度很高,其絕對誤差均在合理范圍以內,因此應用此算法可以很好地用于機床的誤差補償。

表2 各個運動誤差的給定與識別值
5 結論
本次基于對五軸數控機床的誤差模擬研究,提出了有關機床的復雜旋轉角度的運動誤差計算方法,通過Matlab軟件進行了誤差模擬仿真研究,使得對該類數控機床的運動模擬誤差控制大大簡化,也為其提供了相對可靠的誤差模型基礎,對對五軸數控機床零部件加工的位置誤差與姿態誤差補償具有重要意義。

