一種考慮主應力空間的巖石非線性真三軸強度準則

李修磊，陳 臣，凌天清

(1.重慶交通大學 河海學院，重慶 400074；2.重慶交通大學 土木工程學院，重慶 400074)

各種巖體工程中，巖石都會受到地應力場的影響，巖體開挖時應力場會重新分布，復雜應力狀態可能會導致巖石發生變形和破壞。強度準則就是研究各種應力場作用下巖石的強度及確定巖石破壞時的塑性區范圍，是巖石工程穩定性評估和結構優化設計的基礎。由于Mohr-Coulomb(M-C)、Griffith和Hoek-Brown(H-B)強度準則表達式簡單且強度參數物理意義明確，在巖體工程理論和數值計算分析中廣泛應用。其中，M-C準則為線性準則，無法反映巖石強度隨圍壓增加呈非線性增加的關系，因而只適用于低圍壓的情況[1]；雖然Griffith和H-B準則更符合實際情況，但高圍壓下與試驗數據偏差較大[2-3]。為此，一些學者[4-6]改進了M-C和H-B準則，通過減去一個含圍壓的非線性項使其對三軸試驗數據的擬合精度更高，但增加了參數數量及其確定的難度。上述強度準則認為巖石破壞強度只與大和小主應力有關，均未考慮中間主應力的影響，與真三軸試驗數據明顯不符。

大量真三軸試驗結果證明，中主應力對巖石強度有顯著影響[7-9]，一是以中、小主應力相等為初始點，巖石的強度隨著中主應力的增加先增加后減小，但始終高于常規三軸試驗強度；二是巖石越致密堅硬，中主應力效應越大。一些學者在大量試驗和理論分析的基礎上，提出了多種巖石三維強度準則，可歸納為兩類:1)依據強度理論和試驗數據構建新的巖石強度準則表達式，如由Misses強度理論推導的考慮靜水壓力的Drucker-Prager(D-P)強度準則[10]；尤明慶[11]基于試驗數據提出了指數形式的巖石真三軸強度準則，但該準則認為巖石強度隨著中主應力的增加始終是增大的，與真三軸試驗結果明顯不符。2)基于常規三軸強度準則對拉壓過渡帶考慮中主應力修正，如Mogi和俞茂宏分別將中主應力引入M-C準則中，構建了Mogi經驗強度準則和統一強度準則[12-13]，從不同的角度描述了巖石強度的多軸性；張強等[14]在指數型強度準則[2]的基礎上，引入羅德過渡函數導出了巖石三維強度準則；目前主要集中于H-B準則三維化的研究，國內外學者已提出了多種三維化H-B準則，如Priest等[15-19]的研究。這些三維化的H-B強度準則有效地推進了強度理論的發展，但仍未擺脫H-B準則的初始缺點，且存在表達式過于復雜或不滿足偏平面上外凸的強度特性，與真三軸試驗結果差別較大；線性的M-C準則適應性更差。

大量研究結果表明，巖石強度在子午面上隨著靜水壓力的增加而增大，但增加幅度先增大后減小并最終趨于零，經典的M-C和H-B準則無法準確描述巖石強度的這一變化過程。因此，準確的常規三軸強度準則是構建真三軸強度準的基礎。本文將依據從原文獻中搜集的大量常規三軸和真三軸試驗數據，先構建符合子午面上巖石強度變化規律的強度準則，再通過引入中主應力參數和羅德應力參數考慮中主應力的影響，從而建立一種新的巖石非線性真三軸強度準則。

1 現有典型巖石強度準則

1.1 改進的Mohr-Coulomb準則

為了描述巖石強度隨圍壓變化的非線性，Singh等[4]在M-C準則的基礎上減去了一個二次項，提出了改進的Mohr-Coulomb(MM-C)強度準則，表達式如下：

(1)

(2)

式中：c和φ分別為黏聚力和內摩擦角；σcrti為臨界圍壓，通常取為σc；c0和φ0分別為低圍壓下巖石的黏聚力和內摩擦角。當圍壓達到臨界圍壓后(即σ3=σcrti)，式(1)滿足?(σ1-σ3)/?σ3=0，其計算結果為定值。

1.2 Hoek-Brown準則

1980年，Heok和Brown[20]依據大量常規三軸試驗結果，針對完整堅硬巖石提出了帶有經驗性質的Heok-Brown(H-B)強度準則，該準則本身就具有非線性特征，為了使其更具有普適性，隨后又提出了廣義H-B準則[21]，表達式如下：

(σ1-σ3)=σc(mσ3/σc+s)a

(3)

式中：σc為單軸抗壓強度；m、s和a為巖石材料參數，與巖石性質及擾動破碎程度有關。對于完整巖石，為了方便計算分析以及在進行H-B準則的三維化時，通常取s=1.0和a=0.5。

1.3 指數型強度準則

依據常規三軸試驗所得巖石強度隨圍壓的變化關系，You等[2,22]提出了指數型的強度準則，并對比了十幾種準則對試驗結果的預測精度，表明指數型準則最優，其數學表達式如下:

(4)

式中：σc為巖石的單軸抗壓強度，σ∞為巖石的極限主應力差，k0表示σ3=0時巖石強度的影響系數。

1.4 Drucker-Prager準則

1952年，Drucker和Prager[10]在Mises強度準則的基礎上，考慮靜水壓力導出了Drucker-Prager(D-P)準則，該準則屈服面為圓錐體形狀，在π平面上為一簇光滑的圓曲線，表述形式簡潔，應用較為廣泛。以應力不變量表述的D-P準則的表達式如下：

(5)

式中：α和κ為D-P準則參數，I1和J2分別為應力張量第一不變量和偏應力張量第二不變量。

MM-C準則[4]認為三軸等圍壓應力條件下圍壓超過臨界圍壓時巖石抗壓強度不再發生變化，臨界圍壓的確定較為模糊，通常選擇巖石的單軸抗壓強度作為臨界圍壓，所得預測值與試驗結果存在明顯不符。H-B準則[20-21]雖然能夠表征巖石強度隨圍壓增加的非線性變化，但較高圍壓下的預測值明顯大于試驗結果。指數型準則[2, 22]雖然是目前公認預測精度較高的巖石強度準則[6]，由式(4)可知，等圍壓應力條件下巖石的偏應力隨著圍壓的增加始終是增大的，與試驗結果也存在不符之處。以上3種準則均無法預測真三軸應力條件下的巖石強度。D-P準則[10]在等圍壓條件下巖石強度與圍壓將退化為線性關系，無法反映巖石強度隨圍壓的非線性變化。針對上述幾種典型巖石強度準則的不足，以下將基于大量試驗結果提出更符合實際情況的巖石非線性真三軸強度準則。

2 冪函數型巖石強度準則的構建

巖石的強度特性和破壞模型與受到的應力狀態密切相關，巖石的應力狀態通常用大主應力σ1、中主應力σ2和小主應力σ3來表征，主應力之間總要滿足F(σ1,σ2,σ3)≤0。巖石的強度特性主要由常規三軸試驗(σ1>σ2=σ3)測得，即要滿足F(σ1,σ3)≤0，若等號成立F=0，巖石破壞，通常將強度準則寫成如下形式：

σs=f(σ3)

(6)

基于圓柱體巖石試樣的常規三軸試驗結果，利用數學方法可以確定函數f的形式用于描述強度σs與圍壓σ3的關系。

2.1 等圍壓條件下強度準則

根據常規三軸試驗結果，巖石的破壞強度包線在τ-σ坐標系中呈向下凹的非線性特征，隨著圍壓的增加逐漸趨于平緩，圍壓足夠大時為水平線，如圖1所示。Barton[23]將圍壓足夠大時剪切強度不變的初始點定為巖石的臨界狀態，達到臨界狀態后對應的主應力差(σ1-σ3)達到最大值，隨圍壓不再變化，保持為定值。根據圖1中巖石強度包線的變化規律，定義臨界圍壓對應主應力差的最大值為Q∞，令其值為Q∞=(1+k)σc，σc為單軸抗壓強度，k為巖石達到臨界狀態時的影響系數。為了避免確定臨界圍壓帶來的不便和參數的增多，同樣采用以(1+k)σc作為臨界圍壓σcrti，構建一種新的適用于三軸等圍壓條件下的巖石強度準則，表達式如下：

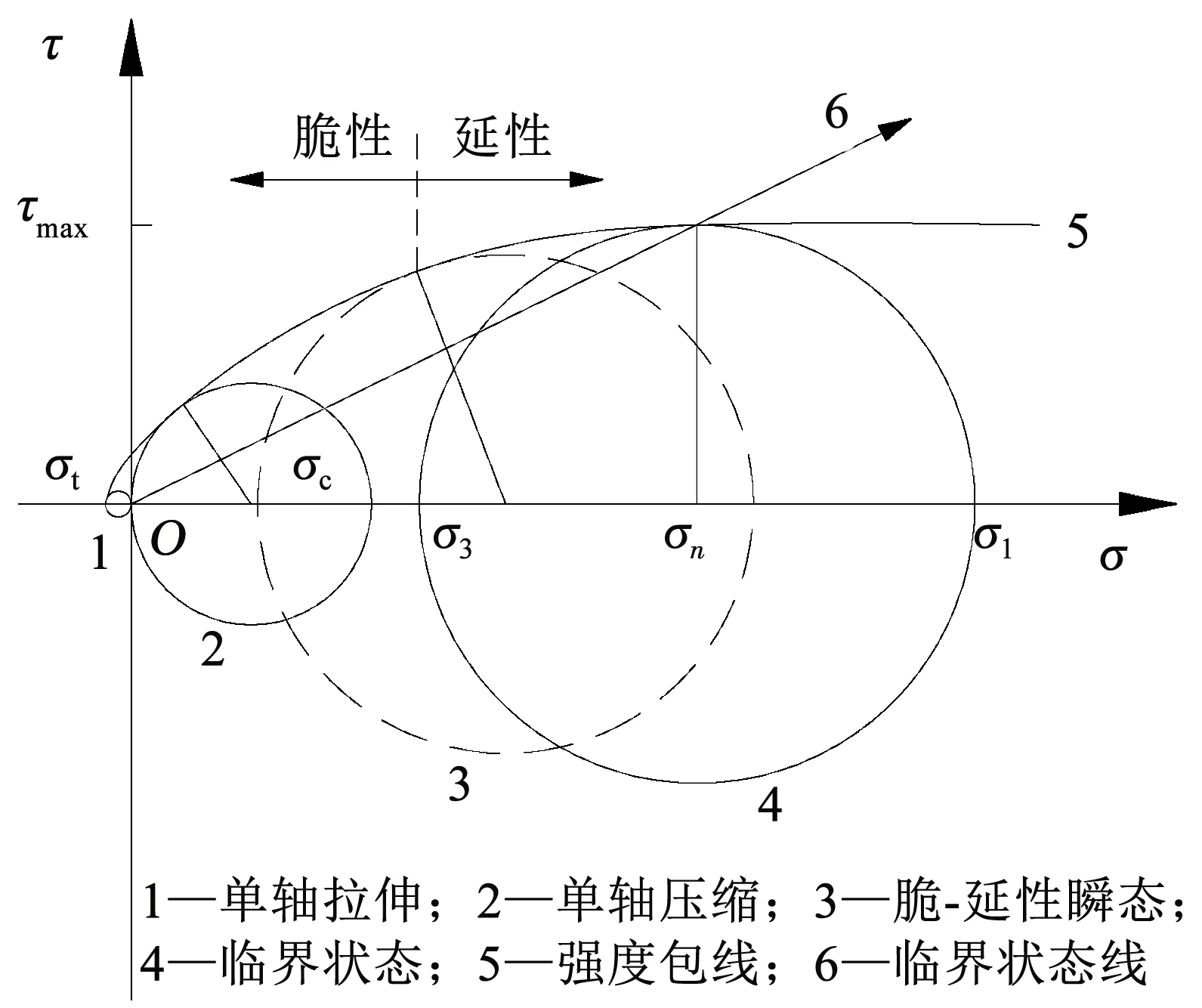
圖1 完整巖石的Mohr圓強度包線

當0≤σ3≤(1+k)σc時,

(7a)

當σ3≥(1+k)σc時，主應力差為定值，即

σs-σ3=(1+k)σc

(7b)

式中：σs為巖石的常規三軸壓縮強度，此時其數值與σ1相等；m為圍壓σ3=0時的影響系數。根據式(7)可知，當σ3=(1+k)σc，則σs=2(1+k)σc，此時巖石的常規三軸壓縮強度等于臨界圍壓的兩倍。對式(7a)進行求導可得m和k之間的關系為

(8)

對式(7a)兩邊取對數，可得

(9)

2.2 真三軸強度準則

巖石力學性質非常復雜，三維應力狀態下表現出顯著的非線性強度特性，在子午面上具有明顯的靜水壓力效應，在偏平面上表現出明顯的中主應力效應[14]。定義中主應力參數β來反映應力狀態如下:

(10)

彈塑性理論中，往往引入羅德應力參數μ以表示中主應力的影響，其代表應力狀態的中主應力與大、小主應力的相對比值，即

(11)

由式(10)和(11)不難證明，μ和β之間存在如下關系:

μ=2β-1

(12)

當μ=-1和β=0時，即σ1>σ2=σ3為常規三軸壓縮試驗；當μ=1和β=1時，即σ1=σ2>σ3為常規三軸拉伸試驗。通常情況下3個主應力之間的關系為σ1>σ2>σ3，則μ介于-1和1；β介于0和1。

考慮小、中主應力對巖石強度的影響，在上述所建等圍壓條件下強度準則(見式(7))的基礎上，引入中主應力參數β和羅德應力參數μ，構建由兩個冪函數公式聯合表示的巖石真三軸強度準則，即

σ1=σs+H(σ2-σ3,σ3)

(13)

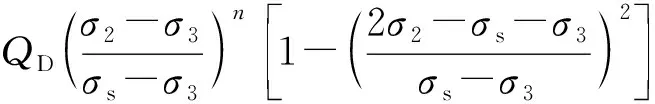
(14)

式中：QD為中主應力影響的巖石強度的最大值；n為巖石強度達到最大值時的參數；當σ2=σ3時滿足H(σ2-σ3,σ3)=0，σ1=σs即為常規三軸壓縮強度，由式(7)求得。

由式(14)對中主應力σ2進行求導，可得

(15)

令?H/?σ2=0，由于真三軸試驗中β≠0，因而有n(1-μ2)-4μβ=0，并結合式(10)～(12)可得

(16)

(17)

小主應力σ3一定的情況下，當中主應力σ2滿足式(17)時，真三軸巖石強度達到最大值。

3 強度準則的評估標準

巖石強度準則參數的確定方法及其預測精度的評估標準有多種形式，根據相關文獻[5]建議采用最小二乘法選擇以均方根誤差(RMSE,ERMS)最小為目標函數來確定強度參數；選擇兩種方法來評估強度準則的預測精度：回歸系數R-平方值(R2)和平均相對誤差(MAPE,EMAP)。 MAPE簡單有效，可直接反映預測誤差的絕對值大小。其中，ERMS、R2和EMAP分別定義為

(18)

(19)

(20)

4 準強度準則驗證及比較

4.1 常規三軸試驗結果驗證及比較

根據已有文獻[5-6,22]報道，統計了12種巖石的常規三軸壓縮試驗結果，將這12種巖石編號為1～12號，分別對應平頂山砂巖、Darley Dale砂巖、錦屏石巖、Bunt砂巖、Carrara大理巖、Yamaguchi大理巖、Cedar石英閃長巖、Indiana石灰巖、Dunham白云巖、Mizuho粗面巖以及Westerly花崗巖。針對上述12種巖石的常規三軸壓縮試驗結果，利用式(7)和(18)在MATLAB軟件中編寫程序確定相關參數(見表1)，得到了所建等圍壓條件下強度準則預測值與巖石試驗強度的對比情況，如圖2所示。可以看出，巖石的常規三軸試驗強度隨著圍壓的增加而增大，增加幅度逐漸減小，且圍壓足夠大時增加幅度近似為零，具有明顯的非線性特征；本文強度準則的預測值曲線與試驗強度曲線有非常高的吻合程度。由表1可知，本文強度準則對所有巖石強度預估的相關性回歸系數R2均在0.98以上，且平均相對誤差EMAP均在4%以下(除7號巖石為6.83%)，如圖5所示。7號巖石(Ceder英云閃長巖)的EMAP略大與其試驗強度的離散程度較大有關，見圖2(b)。以上分析表明本文強度準則能夠很好地預測不同類型巖石在不同圍壓下的試驗強度，具有良好的普遍適用性。

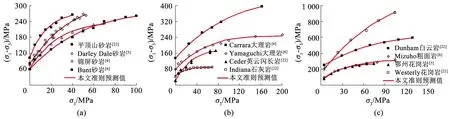
圖2 本文強度準則對12種巖石試驗強度的預測

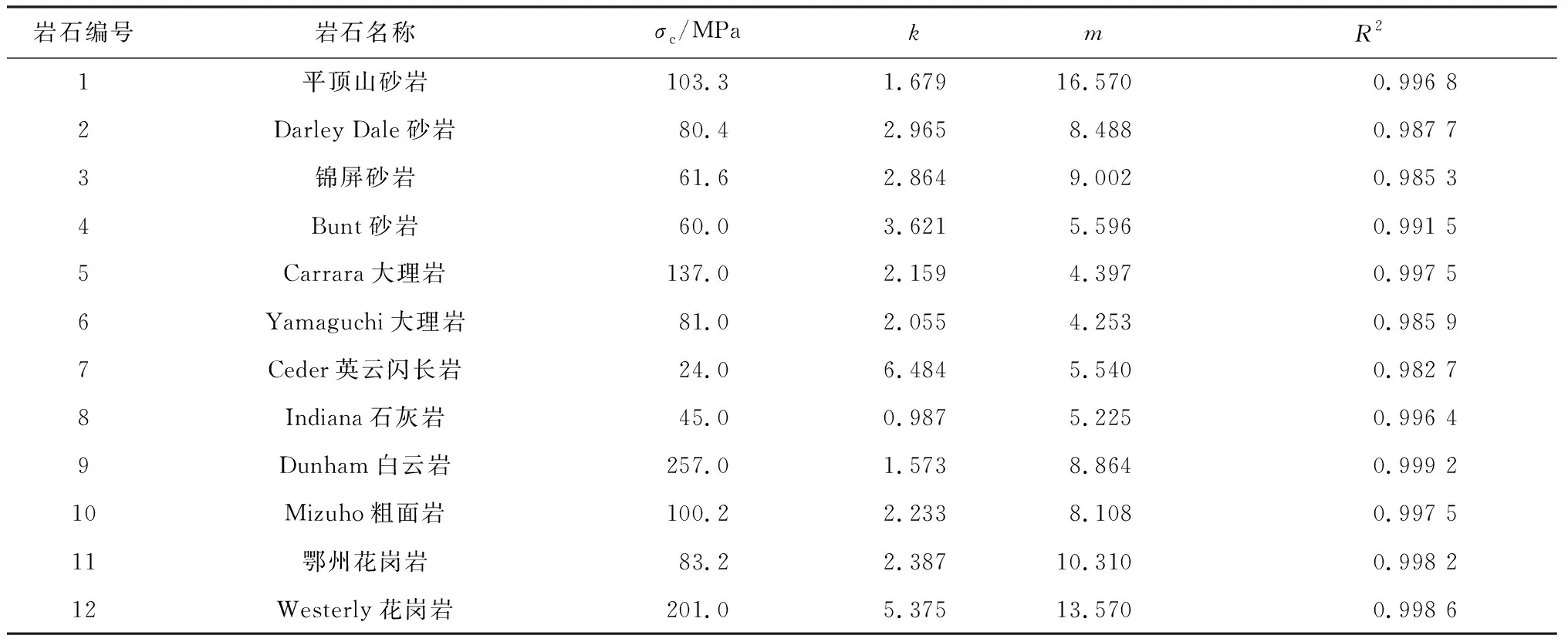
表1 本文準則對巖石常規三軸強度的預測結果

選擇7號Yamaguchi大理巖和11號鄂州花崗巖為對象，充分比對本文強度準則與其他4種典型強度準則之間的差異性，對巖石常規三軸試驗強度的預測情況如圖3所示。

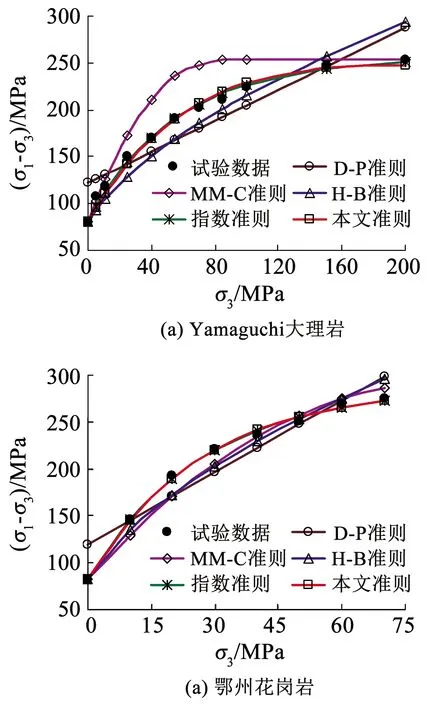
圖3 不同強度準則對不同巖石強度預測的比較

由圖3可以看出，本文強度準則和指數準則(目前被認為預測精度較高的強度準則[6])對巖石試驗強度的預測精度最高，兩者預測值與試驗結果幾乎完全重合；H-B準則的預測值在低圍壓時偏小，而高圍壓時又有明顯的偏大現象；對于MM-C準則，當圍壓超過臨界圍壓(單軸抗壓強度)時巖石強度隨圍壓不再發生變化，導致其預測精度較差；當圍壓小于臨界圍壓時，其預測精度與H-B準則相當；D-P準則退化為常規三軸應力狀態時，巖石強度與圍壓之間是線性關系，故預測精度最差。

為了進一步比較分析上述5種巖石強度準則對巖石強度預測的差異性，圖4、5分別給出了12種巖石的均方根誤差ERMS和平均相對誤差EMAP。同樣可以看出，本文強度準則與指數準則預測得到的不同類型巖石的ERMS和EMAP非常接近，遠小于其他3種強度準則；本文強度準則、指數準則、H-B準則、MM-C準則和D-P準則對所有12種巖石預估所得ERMS的平均值分別為4.431、4.276、10.903、16.804和18.429 MPa，所得EMAP的平均值分別為2.32%、2.43%、5.28%、7.39%和13.74%，也可以看出，本文強度準則和指數準則對巖石強度的預測精度最優，依次是H-B準則、MM-C準則和D-P準則。由表1、圖4、5還可以看出，當圍壓小于單軸抗壓強度σc時， MM-C準則與H-B準則的預測精度相當；當圍壓大于σc時，前者的預測精度將變得很差，與其選擇σc作為臨界圍壓有直接關系。

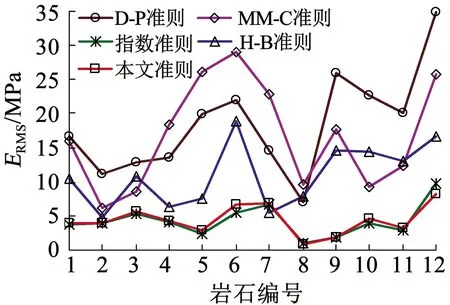
圖4 不同巖石強度準則預測的均方根誤差比較

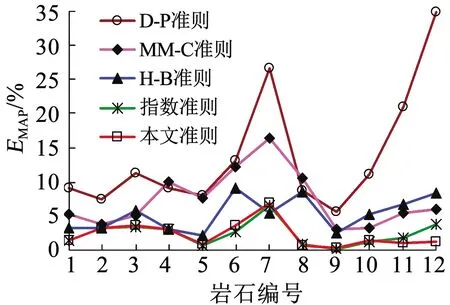
圖5 不同巖石強度準則預測的平均相對誤差比較

4.2 真三軸試驗驗證

真三軸應力條件的巖石試驗強度是評估巖石強度準則的重要方面，利用相關文獻[17-19]報道的8種巖石的真三軸試驗數據對建立的巖石強度準則進行驗證。對這8種巖石進行13～20編號，依次為Westerly花崗巖、KTB閃巖、Dunam白云巖、Mizuho粗面巖、Yuubari板巖、Solenhofen石灰巖、Shirahama砂巖和Manazuru安山巖，利用式(13)～(17)和式(18)在MATLAB軟件中編寫程序，確定這些巖石材料的強度參數，見表2。

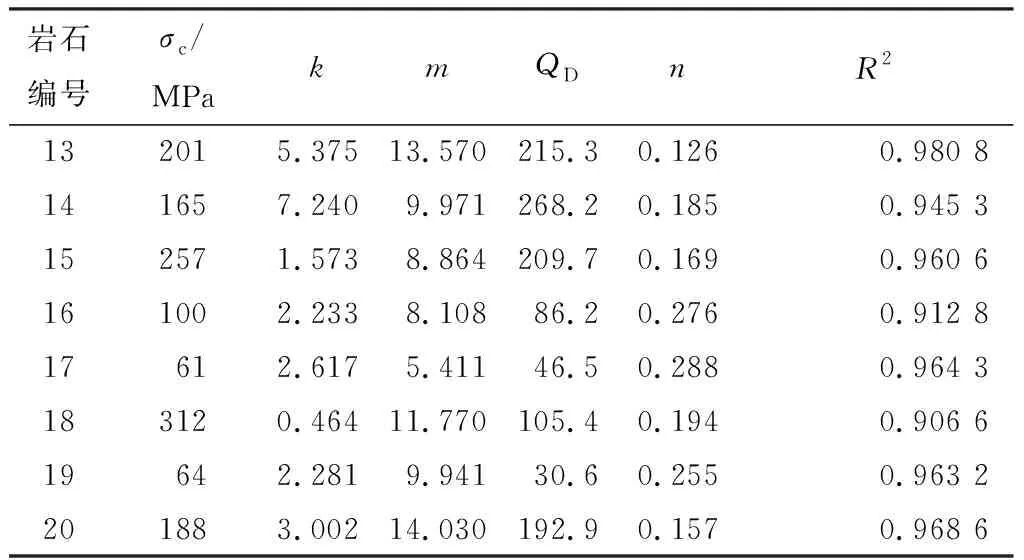
表2 本文準則對巖石真三軸強度的預測結果

圖6給出了所建真三軸強度準則預測值與8種巖石真三軸試驗數據的對比。圖中對角線σ1=σ2和實線σ2=σ3中間所夾上凸形弧狀實線為本文真三軸強度準則的理論計算曲線，左側紅色實線為本文等圍壓條件下強度準則的理論計算曲線；左右側邊界紅色實線分別為常規三軸壓縮和拉伸的狀態線。由圖6可以看出，本文建立的真三軸強度準則與巖石試驗數據有較高的吻合度，能夠較好地反映中主應力效應使巖石強度明顯增強的影響，也很好地反映了巖石強度從常規三軸壓縮到三軸拉伸過程中，巖石強度隨中主應力增加先增大后減小的變化規律；左側σ2=σ3的壓縮曲線與右側σ1=σ2的拉伸狀態線之間的差值呈現出逐漸增大的變化趨勢，由σc逐漸增加到(1+k)σc；由式(7)可知圍壓足夠大時，圖6中左右兩側壓縮和拉伸狀態線為平行線，較好地反映了巖石的靜水壓力效應，但經典的M-C準則、H-B準則和D-P準則并不符合這一規律，這也是本文強度準則的優勢。由表2可知，本文真三軸強度準則對上述8種巖石預估的相關性回歸系數R2均大于0.9，其中有5種巖石超過了0.96。以上說明所建巖石真三軸強度準則能夠較好地預測不同應力狀態下不同類型巖石的強度。

本文強度準則對8種真三軸巖石試驗結果預測得到的均方根誤差ERMS和平均相對誤差EMAP，如圖7所示。可以看出，所建強度準則預測所得的ERMS和EMAP除14號巖石外(分別為74.23 MPa和7.79%)，其余7種巖石均分別在40 MPa和5%以下；14號巖石(KTB閃巖)的ERMS和EMAP相比其他巖石較大，主要原因在于圍壓σ3=150 kPa時真三軸試驗所得KTB閃巖大主應力隨中主應力變化的離散程度非常大(見圖6(b))，導致了所建強度準則對KTB閃巖的預測精度較差。以上分析說明本文強度準則對不同類型巖石的真三軸試驗強度同樣有較高的預測精度，具有良好的普遍適用性。

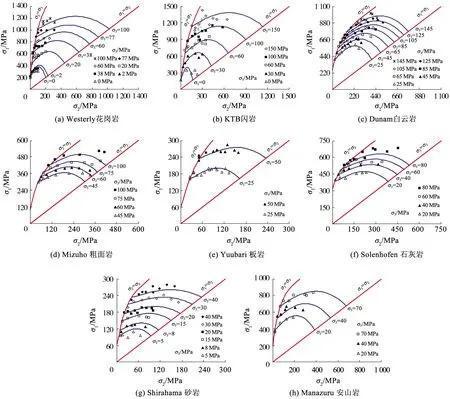
圖6 本文強度準則對8種巖石真三軸試驗強度的預測

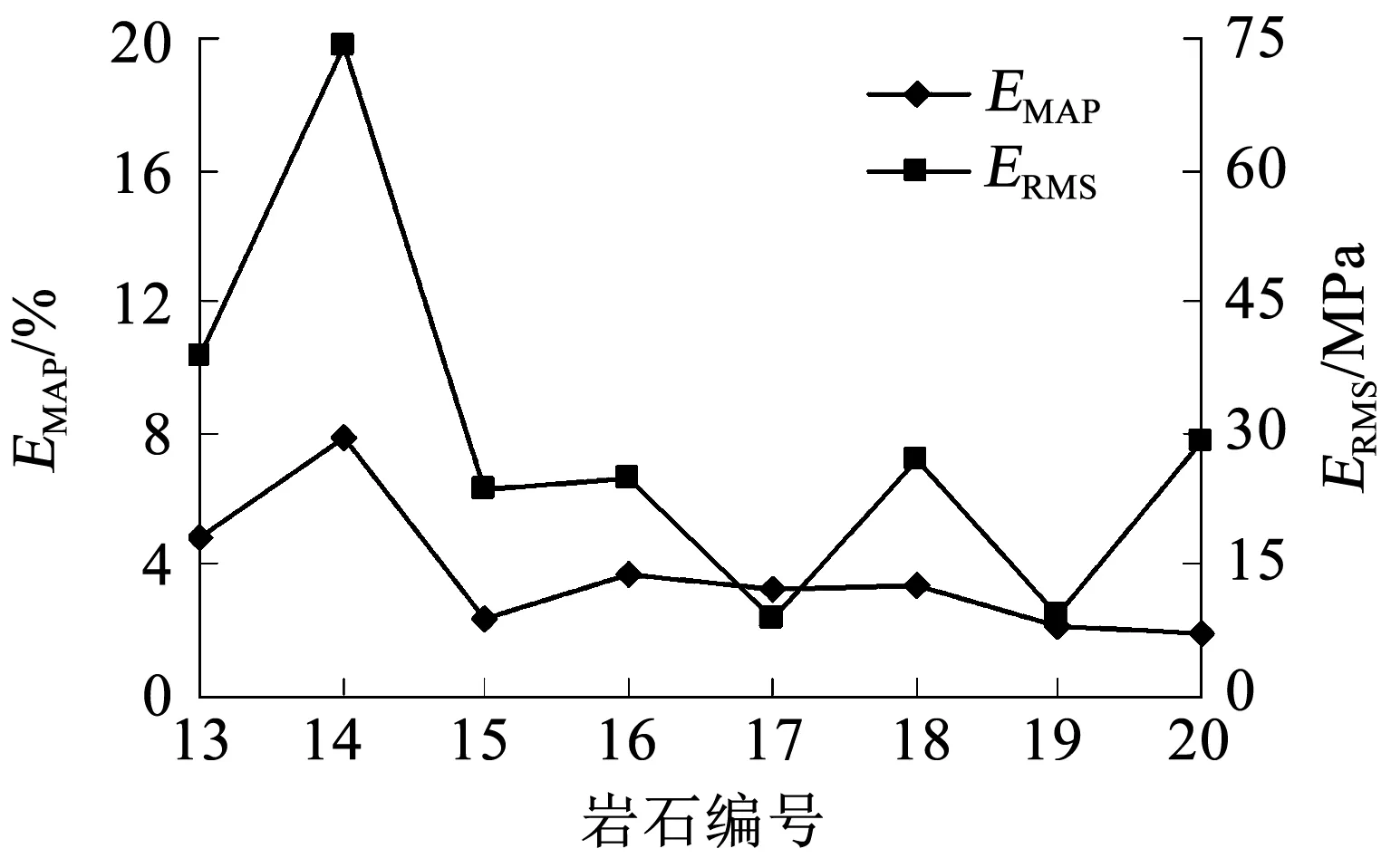
圖7 本文強度準則對8種巖石真三軸試驗結果預測的均方根誤差和平均相對誤差

選擇13號Westerly花崗巖和14號KTB閃巖為對象，對比本文強度準則與已有3種真三軸強度準則[17-19]對巖石真三軸試驗強度的預測情況，分析不同強度準則之間的差異性，如圖8所示。其中，文獻[17-19]均是在H-B準則基礎上建立的真三軸強度準則。可以看出，4種強度準則均可描述小主應力σ3一定時中主應力σ2變化對大主應力σ1的影響規律；文獻[18]所建強度準則顯示σ1受σ2影響幅度很小，預測值與試驗結果差距很大；文獻[19]所建強度準則顯示σ1在σ2較小時達到最大值后又隨σ2快速減小，且多數情況下左側壓縮狀態線上的σ1明顯小于右側拉伸狀態線上的σ1，與實際情況不太相符；相比本文強度準則,多數情況文獻[17]所建強度準則的預測值在σ2較小時略有偏大，在σ2較大時又有所偏小，而本文所建強度準則與試驗結果更為接近。綜合比較，本文強度準則略優于文獻[17]，依次是文獻[19]和文獻[18]提出的強度準則。

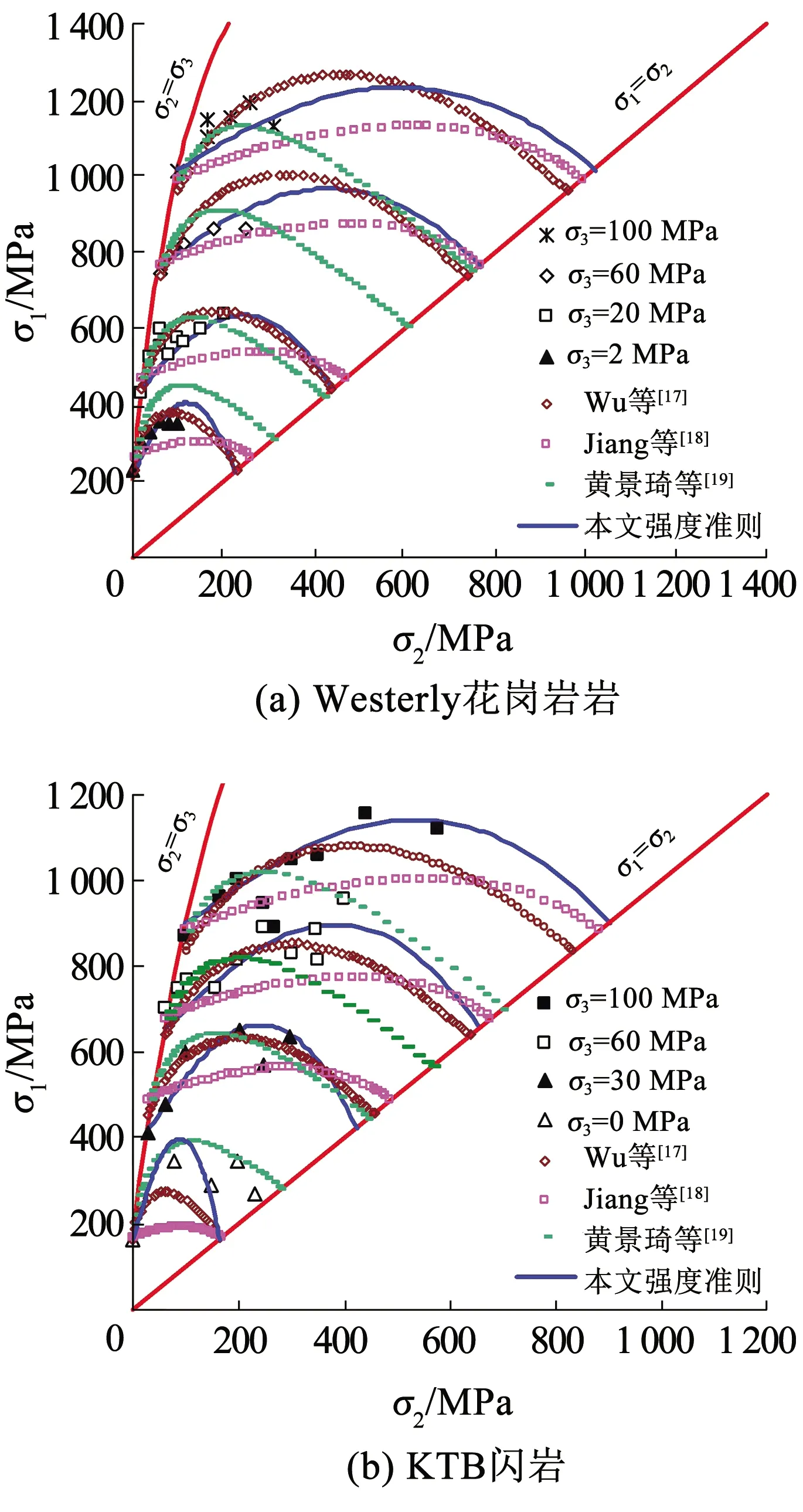
圖8 不同真三軸強度準則對不同巖石強度預測的比較

5 真三軸強度準則的主應力空間

由平均正應力p和廣義剪應力q分別與主應力之間關系可以得到p-q應力空間上強度準則子午面的變化特征；由π平面坐標軸與主應力空間坐標軸之間的關系可以得到強度準則在π平面上的空間特征，計算公式如下

(21)

(22)

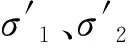
以19號Shirahama砂巖為對象，取表2中的強度參數，所建強度準則的p-q應力空間上子午面和主應力空間偏平面上的形狀特征如圖9所示。

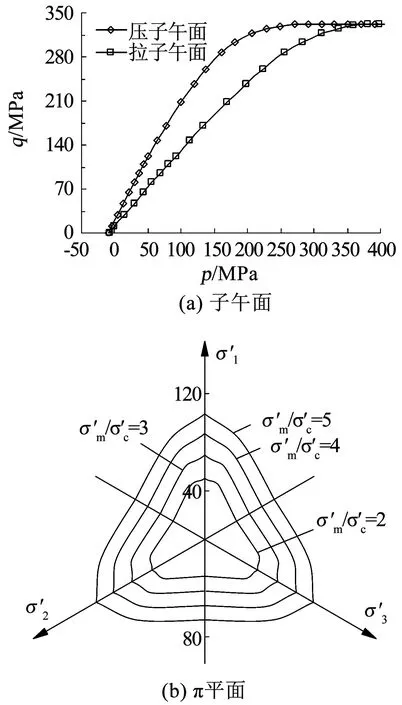
圖9 本文強度準則的空間特征

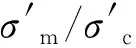
6 結 論

1)12種巖石的常規三軸試驗結果對比表明，本文強度準則預測值與不同類型巖石的試驗強度非常接近，所得相關性系數R2均在0.98以上，本文強度準則、指數準則、H-B準則、MM-C準則和D-P準則對12種巖石常規三軸試驗強度預測所得EMAP的平均值分別為2.32%、2.43%、5.28%、7.39%和13.74%，本文強度準則略好于指數準則，后3種準則的預測精度依次降低，說明本文強度準則具有良好的普遍適用性。

2)8種巖石的真三軸試驗結果對比表明，本文強度準則與不同類型巖石的試驗強度吻合程度較好，能夠很好地反映大主應力隨中主應力的增加呈先增大后減小的變化規律，所得R2均在0.9以上(有5種巖石的R2大于0.96)，說明本文強度準則能夠較好地預測不同應力狀態下巖石的真三軸試驗強度。

3)本文強度準則在拉、壓子午面上的偏應力差值隨平均正應力由零逐漸增加再逐漸減小為零，在π平面上近似為一簇連續頂角外凸的曲線三角形，且隨著平均正應力增加逐漸向外擴展，拉、壓區間呈弧形過渡，很好地反映了巖石靜水壓力效應和中主應力對大主應力的影響規律。