基于數(shù)學(xué)建模的高中數(shù)學(xué)教學(xué)策略探究

張芝悅

[摘? 要] 數(shù)學(xué)建模是深化數(shù)學(xué)概念、原理、定理等知識(shí)的理解和應(yīng)用數(shù)學(xué)知識(shí)解決實(shí)際情境問(wèn)題的基本手段. 文章在分析基于數(shù)學(xué)建模的高中數(shù)學(xué)教學(xué)原則的基礎(chǔ)上，以《三角函數(shù)的應(yīng)用》為例探究了基于數(shù)學(xué)建模的高中數(shù)學(xué)教學(xué)策略.

[關(guān)鍵詞] 數(shù)學(xué)建模;高中數(shù)學(xué);策略

高中數(shù)學(xué)教學(xué)不僅要注重相關(guān)概念和數(shù)學(xué)方法的深度理解，培養(yǎng)學(xué)生從日常生活中發(fā)現(xiàn)問(wèn)題、分析問(wèn)題的意識(shí)，而且也要理論聯(lián)系實(shí)際，有效提高學(xué)生應(yīng)用所學(xué)知識(shí)解決實(shí)際問(wèn)題的能力. 而作為高中學(xué)生必備的數(shù)學(xué)核心素養(yǎng)之一，數(shù)學(xué)建模素養(yǎng)不僅能夠培養(yǎng)學(xué)生應(yīng)用數(shù)學(xué)語(yǔ)言表達(dá)實(shí)際問(wèn)題的能力，而且也能反過(guò)來(lái)利用模型思想鞏固所學(xué)知識(shí)，深化相關(guān)概念、原理、定理等知識(shí)的理解. 因此，以提高數(shù)學(xué)建模素養(yǎng)為核心，探究高中數(shù)學(xué)教學(xué)方式具有重要的意義.

[?]基于數(shù)學(xué)建模的高中數(shù)學(xué)教學(xué)原則

1. 激發(fā)興趣原則

在高中數(shù)學(xué)建模素養(yǎng)培養(yǎng)中，教師應(yīng)最大限度地讓學(xué)生了解數(shù)學(xué)建模的魅力，使學(xué)生具有強(qiáng)烈的意愿自主地開(kāi)展探究性學(xué)習(xí). 例如，在教學(xué)《三角函數(shù)的應(yīng)用》時(shí)，教師請(qǐng)學(xué)生扮演船長(zhǎng)，并詢問(wèn)“船長(zhǎng)”面對(duì)如下問(wèn)題時(shí)該如何處理：“當(dāng)貨船航行到九江港時(shí)，你最想獲得哪方面信息”“如何調(diào)查港口水深與日期時(shí)間的關(guān)系”“面對(duì)貨船被擱淺的風(fēng)險(xiǎn)，如何選擇合理的港口進(jìn)出時(shí)間”，由此激發(fā)學(xué)生探究的興趣，促使學(xué)生嘗試解決實(shí)際問(wèn)題中所蘊(yùn)含的數(shù)學(xué)信息.

2. 聯(lián)系實(shí)際原則

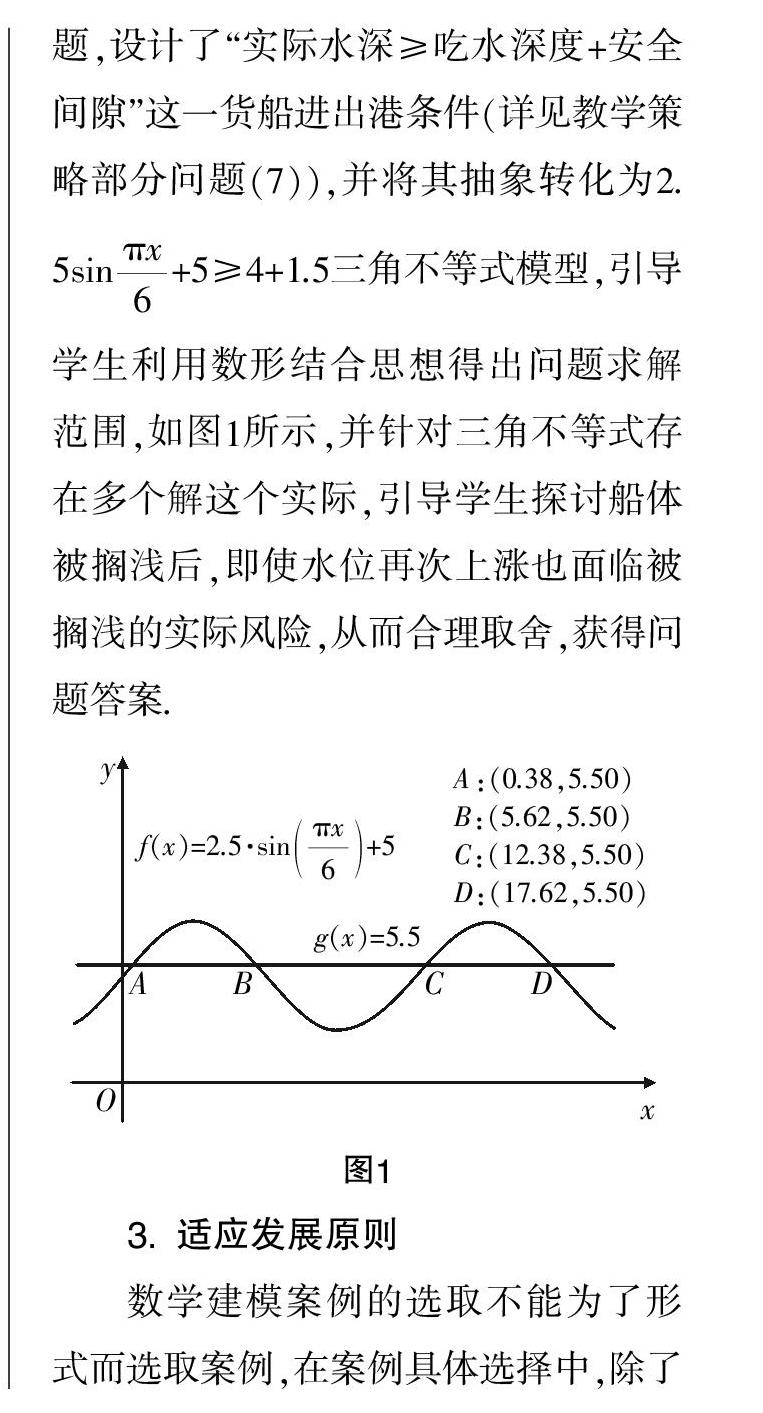
為了更加真實(shí)地刻畫現(xiàn)實(shí)世界是高中數(shù)學(xué)建模的核心，因此，在設(shè)計(jì)和選擇數(shù)學(xué)建模主題時(shí)，教師應(yīng)從學(xué)生熟悉的日常生活場(chǎng)景著手，有效促使學(xué)生感受數(shù)學(xué)建模的真實(shí)性. 同時(shí)，教師還應(yīng)及時(shí)引導(dǎo)學(xué)生發(fā)現(xiàn)問(wèn)題，求解和驗(yàn)證所建立的數(shù)學(xué)模型，從而將教學(xué)中所學(xué)習(xí)到的知識(shí)與實(shí)際生活相聯(lián)系. 例如，貨船吃水深度是實(shí)際生活中經(jīng)常所聽(tīng)到的概念，因此，教師應(yīng)結(jié)合航行安全問(wèn)題，設(shè)計(jì)了“實(shí)際水深≥吃水深度+安全間隙”這一貨船進(jìn)出港條件（詳見(jiàn)教學(xué)策略部分問(wèn)題（7）），并將其抽象轉(zhuǎn)化為2.5sin+5≥4+1.5三角不等式模型，引導(dǎo)學(xué)生利用數(shù)形結(jié)合思想得出問(wèn)題求解范圍，如圖1所示，并針對(duì)三角不等式存在多個(gè)解這個(gè)實(shí)際，引導(dǎo)學(xué)生探討船體被擱淺后，即使水位再次上漲也面臨被擱淺的實(shí)際風(fēng)險(xiǎn)，從而合理取舍，獲得問(wèn)題答案.

3. 適應(yīng)發(fā)展原則

數(shù)學(xué)建模案例的選取不能為了形式而選取案例，在案例具體選擇中，除了要滿足學(xué)生的心理發(fā)展特征和智力發(fā)展水平外，還應(yīng)遵循因人而異、適時(shí)發(fā)展的原則，在合理的教學(xué)階段選擇適當(dāng)?shù)默F(xiàn)實(shí)問(wèn)題. 例如，對(duì)于初次接觸數(shù)學(xué)建模思想的學(xué)生，教師應(yīng)重點(diǎn)培養(yǎng)學(xué)生應(yīng)用數(shù)學(xué)知識(shí)描述現(xiàn)實(shí)問(wèn)題的能力，注重將教材中的例題或習(xí)題進(jìn)行改編;對(duì)于已經(jīng)具備數(shù)學(xué)建模意識(shí)的學(xué)生，教師應(yīng)將教學(xué)的重點(diǎn)放置在真實(shí)情景中抽象出數(shù)學(xué)概念和數(shù)學(xué)模型的能力;對(duì)于已經(jīng)熟悉建模過(guò)程的較高階段的學(xué)生，教師應(yīng)選擇較為完整的實(shí)際問(wèn)題，及時(shí)引導(dǎo)學(xué)生經(jīng)歷數(shù)據(jù)收集、模型建立、模型驗(yàn)證、模型對(duì)比等過(guò)程，不斷提升學(xué)生的數(shù)學(xué)建模素養(yǎng).

[?]基于數(shù)學(xué)建模的高中數(shù)學(xué)教學(xué)策略

1. 創(chuàng)設(shè)問(wèn)題情境，培養(yǎng)數(shù)學(xué)化能力

數(shù)學(xué)核心素養(yǎng)的提高必須借助數(shù)學(xué)化過(guò)程，并且缺乏問(wèn)題情境的教學(xué)是空洞的，因此，教師應(yīng)從學(xué)生實(shí)際生活出發(fā)，結(jié)合教學(xué)目標(biāo)和所授內(nèi)容，創(chuàng)設(shè)學(xué)生感興趣的問(wèn)題情境，促使學(xué)生找出現(xiàn)實(shí)情境與數(shù)學(xué)知識(shí)之間的規(guī)律與聯(lián)系，并從數(shù)學(xué)的視角出發(fā)，應(yīng)用數(shù)學(xué)知識(shí)和方法將其轉(zhuǎn)化為數(shù)學(xué)問(wèn)題加以分析.

例如，在組織學(xué)生學(xué)習(xí)完三角函數(shù)知識(shí)時(shí)，教師應(yīng)根據(jù)所授內(nèi)容，利用視頻播放九江港碼頭漲潮時(shí)貨船駛?cè)牒降劳？看a頭進(jìn)行裝卸，落潮時(shí)及時(shí)返回的生活場(chǎng)景. 在此基礎(chǔ)上，設(shè)計(jì)如下問(wèn)題串要求學(xué)生應(yīng)用已學(xué)知識(shí)發(fā)現(xiàn)問(wèn)題情境中所蘊(yùn)藏的數(shù)學(xué)規(guī)律.

（1）貨船為什么在漲潮時(shí)駛?cè)牒降溃瑸槭裁丛诼涑睍r(shí)返回？

（2）假如你就是船長(zhǎng)，你最想了解該港口哪方面的信息？

（3）如果讓你調(diào)查港口水深與日期時(shí)間的關(guān)系，你會(huì)采用哪些方式？

（4）假如表1所反饋的是某一日九江港時(shí)間與水深之間關(guān)系，你能從中獲取哪些有用信息？

2. 滲透建模思想，促進(jìn)實(shí)踐應(yīng)用能力

思維品質(zhì)與關(guān)鍵能力是數(shù)學(xué)核心素養(yǎng)的本質(zhì)，而模型思想可以有效幫助學(xué)生理解數(shù)學(xué)概念、原理的本質(zhì)與規(guī)律，解決現(xiàn)實(shí)生活中的某一類問(wèn)題，并且，數(shù)學(xué)的實(shí)踐應(yīng)用能力正好體現(xiàn)了數(shù)學(xué)建模素養(yǎng)的關(guān)鍵能力，因此，教師應(yīng)按照“生活問(wèn)題—建立模型—求解模型—解釋結(jié)果”的思路，不斷滲透建模思想和方法，促使學(xué)生有效體驗(yàn)完整的數(shù)學(xué)建模過(guò)程. 值得強(qiáng)調(diào)的是，由于課時(shí)的有限性，教師應(yīng)將數(shù)據(jù)的收集等過(guò)程最大限度地留置在課外交流合作中完成.

例如，在上述問(wèn)題情境創(chuàng)設(shè)和實(shí)際問(wèn)題數(shù)學(xué)化之后，教師應(yīng)及時(shí)通過(guò)如下教學(xué)方式滲透建模思想與方法.

（5）我們學(xué)習(xí)過(guò)的函數(shù)模型有哪些，能否應(yīng)用相關(guān)數(shù)學(xué)模型描述九江港水深與時(shí)間的變化關(guān)系？

（6）在直角坐標(biāo)系中畫出以上數(shù)據(jù)的散點(diǎn)圖，并計(jì)算相關(guān)函數(shù)模型.

3. 注重回顧反思，提升創(chuàng)造遷移能力

數(shù)學(xué)的學(xué)習(xí)是理解與反思的過(guò)程，學(xué)生有了疑惑才能主動(dòng)深入地探究和思考，并且數(shù)學(xué)建模還是一個(gè)循序漸進(jìn)的過(guò)程，因此，教師應(yīng)及時(shí)引導(dǎo)學(xué)生反思建模過(guò)程，鼓勵(lì)學(xué)生大膽地提出自己的猜想和疑惑，啟發(fā)學(xué)生提出新的問(wèn)題.? 同時(shí)，教師還應(yīng)幫助學(xué)生通過(guò)思維導(dǎo)圖等方式組織學(xué)生及時(shí)進(jìn)行歸納總結(jié)，有效培養(yǎng)學(xué)生的知識(shí)遷移能力. 仍以上述案例教學(xué)為例，在上述相關(guān)函數(shù)模型獲得之后，為了研究的深入，教師還應(yīng)設(shè)計(jì)如下問(wèn)題及時(shí)引導(dǎo)學(xué)生不斷回顧反思，促進(jìn)學(xué)生數(shù)學(xué)建模素養(yǎng)的提高.

（7）由于每艘貨船的吃水深度是不同的，并且根據(jù)安全規(guī)定船只航行時(shí)其船底與河道之間的距離必須大于1.5米，若有一艘吃水為4米的貨船，試問(wèn)該船什么時(shí)間才能駛?cè)敫劭冢诟劭谧疃嗄芡Ａ舳嚅L(zhǎng)時(shí)間才能不被擱淺？

（8）已知某一貨船14：00開(kāi)始裝卸貨物，若吃水深度以0.3 m/h的速度下降，并且其他條件同上述問(wèn)題（7），為了防止該船被擱淺，試問(wèn)這艘貨船必須在何時(shí)之前停止裝卸駛向更深水域？

4. 多元化過(guò)程性評(píng)價(jià)，提高合作探究能力

簡(jiǎn)單的應(yīng)用題測(cè)試無(wú)法激發(fā)學(xué)生數(shù)學(xué)建模探究的興趣，也無(wú)法在數(shù)學(xué)建模教學(xué)中起到良好的教學(xué)效果，并且，學(xué)生對(duì)同一問(wèn)題的理解是不同的，因此，教師應(yīng)摒棄以成績(jī)?yōu)槲ㄒ粯?biāo)準(zhǔn)的評(píng)價(jià)體系，實(shí)施多元化和多樣化教學(xué)評(píng)價(jià)，注重學(xué)生自評(píng)、互評(píng)、開(kāi)放題的測(cè)試、小論文等形式，有效掌握數(shù)學(xué)建模中學(xué)生思維品質(zhì)、關(guān)鍵能力以及存在的不足. 特別是對(duì)于學(xué)生數(shù)學(xué)建模過(guò)程中暫時(shí)找不到問(wèn)題解決思路和方法的學(xué)生教師應(yīng)及時(shí)給予鼓勵(lì)和指導(dǎo)，幫助其樹(shù)立信心;對(duì)于學(xué)生數(shù)學(xué)建模過(guò)程中呈現(xiàn)出的創(chuàng)造性建議教師應(yīng)及時(shí)給予肯定.

例如，在上述案例中，教師可以從以下幾個(gè)方面進(jìn)行多元化的過(guò)程性評(píng)價(jià)：

①學(xué)生討論發(fā)言、結(jié)果匯報(bào)中的表現(xiàn);②數(shù)據(jù)收集、分析的方法是否合理;③模型的建立是否符合案例實(shí)際;④建模過(guò)程中解決困難的機(jī)制和辦法;⑤模型反思，或提出新的探究問(wèn)題;⑥小組合作和計(jì)算過(guò)程中學(xué)生的狀態(tài).

總之，教學(xué)活動(dòng)中，教師應(yīng)充分發(fā)揮學(xué)生這一數(shù)學(xué)建模活動(dòng)的主體作用，通過(guò)創(chuàng)設(shè)問(wèn)題情境、引導(dǎo)學(xué)生建立和求解數(shù)學(xué)模型、貫穿過(guò)程性評(píng)價(jià)、注重回顧反思等策略，有效提升學(xué)生的數(shù)學(xué)化、合作探究、實(shí)踐應(yīng)用等能力.