求解鐵路物流配送中心選址問題的改進灰狼優化算法

郝芃斐，池 瑞，屈志堅，涂宏斌，池學鑫，張地友

（華東交通大學電氣與自動化工程學院，南昌 330013）

0 引言

近年來，市場各種類型的物流形式都在不斷地擴大著其服務的范圍，爭取實現物流中心的最大輻射范圍和最佳利用率。鐵路物流配送中心作為物流體系的重要基礎設施，它具有速度快、費用低、運量大、連續性好的優點，在交通和物流業中發揮重要作用。鐵路物流中心的建設對提升鐵路貨物運輸服務品質、提供鐵路物流可持續發展的基礎設施具有重要意義［1］。

國內學者對于物流選址的問題進行了大量的研究分析。傳統的求解方法主要有三種，分別是分支定界法、重心法與拉格朗日松弛法［2］，其中，分支定界法常用來解決小規模選址問題；重心法主要用于求解單一物流配送中心選址問題；拉格朗日松弛法則是可以求取中等規模問題的次優解。由于鐵路物流配送中心選址模型是帶有復雜約束的非線性模型，屬于典型的NP-hard 問題［3］，而傳統的群智能算法，像基本灰狼優化算法（Grey Wolf Optimizer，GWO）在迭代后期易陷于局部最優并且收斂精度不高［4］，無法很好地解決鐵路物流中心選址的問題。目前，很多研究者通過運用一些智能算法與實際選址問題相結合來研究這個問題，如：袁群等［5］通過遺傳算法（Genetic Algorithm，GA）和禁忌搜索算法相結合，并用貪婪算法改進基本遺傳算法來有效避免早熟及局部最優現象，提高了求解物流選址最優解的效率；李茂林［6］為了解決傳統猴群算法全局收斂度低的問題，通過非線性調節因子和lateral 變異策略對算法進行改進，最后將改進后的猴群優化算法用于物流配送中心選址的實際問題中；生力軍［7］針對經典粒子群算法在解決物流選址問題時易早熟收斂并且只能得到局部最優解的問題，提出了量子粒子群算法來求取物流配送中心選址的最優解；李小川等［8］將人群搜索算法中的行為意識引入煙花算法，來避免基本煙花算法魯棒性差的缺陷。盡管上述優化算法可以求得所需解，但單一機制的群智能優化算法無法滿足求解具有多個配送點與需求點的鐵路物流配送中心位置的需要，因此本文提出一種改進的灰狼優化算法。

基本灰狼優化算法（GWO）是Mirjalili 等［9］提出的一種新調整參數少的群體智能算法，原理簡單且易于實現，但容易在迭代后期陷于局部最優，影響收斂速度及精度［10］。因此本文從尋找最佳的鐵路物流配送中心位置出發，以求解31 個需求點、6 個配送中心的中等規模鐵路物流中心選址為模型，提出一種帶有佳點集和差值剔除策略的改進灰狼優化算法（Improved Grey Wolf Optimization，IGWO），最后將改進的灰狼優化算法用于求解中等規模的鐵路物流配送中心選址問題上。

1 鐵路物流中心選址模型

在鐵路物流中心選址問題中，由于鐵路物流中心自身的特殊性，一般情況下鐵路物流中心為中大規模，運輸主要以大宗貨物為主，適宜遠距離運輸，所以鐵路物流中心的選擇很大程度上決定了鐵路物流運輸的發展［11］。

1.1 鐵路物流中心選址問題模型假設

為了構建適當的模型，提出以下假設：

1）在已有的鐵路物流中心所輻射到的服務及配送區域的需求總量上，物流中心自身的負荷工作能力恒滿足其配送及服務區域的總需求量。

2）在物流中心所限區域范圍內，滿足一一對應的服務。3）將鐵路物流中心與其配送和服務區域的需求點之間的距離以及產生的費用作為主要考慮因素。

4）在費用計算中加入一個懲罰值，當物流中心與配送點距離大于3 000 km時需要考慮到這個懲罰值。

5）以降低距離產生的費用為目標，通過限定規范營運費用，可有效控制運營成本。

1.2 鐵路物流中心選址問題模型構建

基于以上5 點假設，通過具有普遍性和代表性的物流選址模型問題影響因素分析，從M個備用鐵路物流配送中心中找出m個物流配送中心向n個需求點進行配送服務，選取并建立了如下物流選址模型［12］。

目標函數：

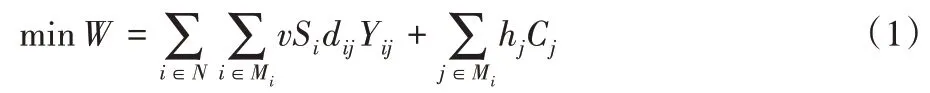
約束條件：

其中：目標函數W是各鐵路物流配送中心到需求點的運費與配送中心所需建設費用之和；N為所有需求點的序號集合；Mi是所有備用配送中心與需求點i之間的距離小于s的集合；s為距離上限；v為運費率；wi為需求點i的需求量；dij為需求點i與其最近鐵路物流配送中心j的距離；Cj為鐵路物流配送中心的固定成本；p為從備選鐵路物流中心選出的物流中心總和數；Yij、hj為0-1變量。

式（1）代表所有鐵路物流中心運營成本總和，構成模型的目標函數；式（2）可保證每個配送點與物流中心之間的一一對應關系；式（3）表示只有當備選的物流配送中心被選中才可以提供相應服務；式（4）表示從物流配送中心到需求點距離不超過s；式（5）表示鐵路物流配送中心數為p；式（6）表示當決策變量為1 時，表示備選物流配送中心被選中，并由其供應需求點i的需求量，否則為0。

2 標準灰狼優化算法

灰狼是一種以群居生活為主的頂級食肉動物，它們有著嚴格的社會等級制度［13］。通常每個群體中有5～12 只狼，其中第1 層稱為α，是灰狼種群中的最高領導者，負責決策各項事務；第2 層稱為β，在整個種群中協助頭狼α；第3 層稱為δ，主要負責偵察以及狩獵等事務，嚴格遵守α和β的指令；第4層稱為ω，它聽從于其他所有階層的指令。當灰狼在包圍獵物的過程中，它們的行為可以表達為：

其中：式（7）表示灰狼自身與獵物的距離；式（8）表示灰狼X在算法第t+1 代時的位置；式（9）、（10）用于計算系數向量A與C；收斂因子a按照式（18）從2～0 線性減少，r1和r2是在0～1 隨機產生的向量。

當灰狼發現獵物的位置時，狼群會逐漸包圍獵物，第4 層的ω狼會根據α、β、δ灰狼的位置更新位置，數學模型如下：

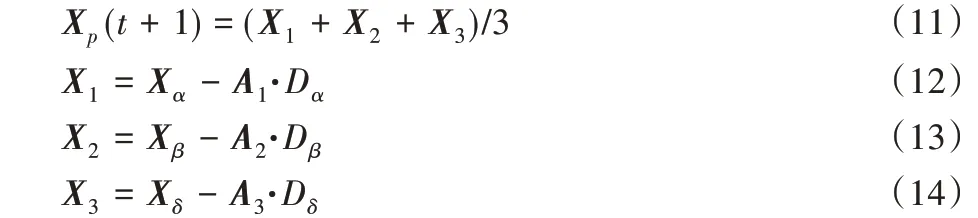
其中：式（12）、（13）和（14）中的A1、A2、A3由式（9）計算得出；Dα、Dβ、Dδ的定義如式（15）、（16）和（17）所示；C1、C2、C3由式（10）計算得出。

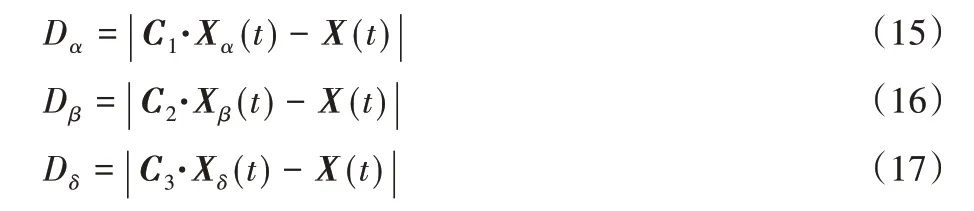
當灰狼終止移動的時候準備開始攻擊獵物。隨著迭代次數的增加，a的值在2～0線性減小，更新如式（18）所示：

其中Tmax表示最大迭代次數。

3 改進的灰狼算法

在基本的灰狼算法中，初始種群是隨機產生的，并且根據式（11）～（14）來進行位置更新，但是每次迭代前后并未進行信息交換。針對以上基本灰狼算法的不足，提出如下改進的灰狼優化算法（IGWO）。

3.1 基于佳點集的種群初始化方法

初始種群在搜索空間內均分布能夠使得種群具有更強的多樣性，進而有助于提高算法的全局搜索能力。用佳點集（Good Point Set，GPS）理論的取點法代替隨機法可以使個體在空間中更加可靠地均勻分布，提高算法穩定性［14］。比起最初灰狼算法隨機產生的辦法，佳點集初始種群更具有穩定性和遍歷性。

佳點集的基本定義與性質為：

1）設Gs是s維歐氏空間中的單位立方體，即x∈Gs，，1 ≤k≤n}。

2）當r=，則說明p就是滿足s≤(p-3)2的最小素數，此時對應的r為所求佳點。

3）若Pn的偏差含量滿足?(n)=C(r，ε)nε-1，其中r為佳點，Pn(k)稱為佳點集，ε是隨機產生的任意正數，C(r，ε)是有且只和r、ε有關的常量。

3.2 差值剔除策略

基本GWO在處理一些高維數問題時，在迭代后期收斂速度慢、易陷入局部最優［15］。本文受到布谷鳥搜索（Cuckoo Search）算法的啟發，可以通過概率刪除方式，根據一定概率Pa剔除GWO中的差解，并產生對應規模的新解的方法。通過在標準灰狼算法完成位置更新后加入差值剔除策略（D-value Elimination Strategy，DES）這一方法來提高算法的尋優能力。

差值以概率Pa剔除后，按如下計算式產生對應規模的新解：

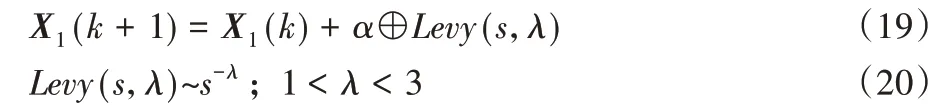
根據式（19）～（20）生成一個新的解替換更新X。差值剔除策略增強了算法的局部尋優能力，有效避免了處理問題時陷于局部最優的情況，增加算法找到最優解的概率。

3.3 IGWO算法步驟

本文提出的IGWO算法步驟如下：

步驟1 設定算法參數。包括種群規模、最大迭代次數、上下界以及維數，令迭代次數的初始值l=0，根據式（9）～（10）在搜索空間中隨機生成控制參數。

步驟2 種群初始化。在搜索空間中利用佳點集初始化種群的方法生成最初的初始種群以及對應位置。

步驟3 根據適應度函數對灰狼位置進行更新，計算出每個灰狼個體此時位置的適應值。若灰狼當前的位置優于自身記憶的最優位置，則用當前位置替代它；若目前全局搜索的最優位置優于到當前為止搜尋到的最優位置，就用全局最優的位置替代。

步驟4 將適應度值排列前三位置的灰狼個體記為α、β、δ，它們對應的位置記為Xα、Xβ、Xδ，Xα作為主導的位置。

步驟5 按照式（12）～（14）計算其余灰狼個體與α、β、δ灰狼之間的位置，并且根據式（15）～（17）更新當前其余灰狼個體的位置。

步驟6 對當前最優的灰狼個體α的位置進行式（19）～（20）操作，增加最優位置Xα的局部尋優能力。

步驟7 更新步驟1 中隨機產生的參數r、A、C的值，再令l=l+1，返回步驟3循環，直到迭代次數達到最大限制值。

4 數值仿真

為測試本文提出的改進灰狼優化算法（IGWO）的優化效果進行大量的Matlab數值仿真實驗，并且與基本GWO進行了比較。選取了10 個測試函數（如表1 所示），兩種算法種群規模均取30，最大迭代次數取500。

表1 十個測試函數Tab.1 Ten test functions

4.1 佳點集初始化種群的仿真分析

采用佳點集來改進基本GWO初始種群的方法，有效提高了算法的全局收斂性以及搜索效率。為了更加直觀看出利用佳點集初始種群帶來的優化性與可行性，選取了在6 個具有代表性的測試函數下，單獨加入佳點集初始化種群（GWOGPS），來驗證算法的有效性。當測試函數在30 維的情況下，將6 個測試函數Schwefel’s 2.22 函數、Sphere 函數、Zakharov函數、Sum Square 函數、Ackley 函數以及Rastrigin 函數針對適應度值的結果進行實驗比對，如圖1所示。

通過圖1 可以看出，在算法中單獨加入佳點集可以有效提高基本GWO的尋優結果，通過在實驗中單獨加入佳點集來初始化種群，使GWO-GPS 可以很快找到最優結果，但依舊存在對于某些函數的尋優結果并不是特別理想，只在部分迭代次數階段有效。總之，單獨加入佳點集初始化種群可以提高大部分基本GWO 的尋優結果，只對有部分測試函數具有局限性。

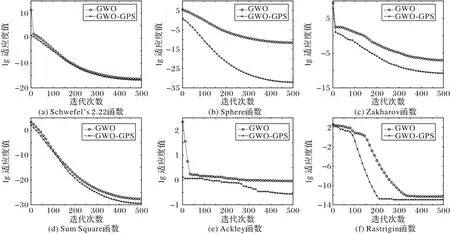
圖1 GWO與GWO-GPS的尋優結果比較Fig.1 Optimization results comparison of GWO and GWO-GPS

4.2 差值剔除策略的仿真分析

通過典型測試函數尋優實驗，發現加入差值剔除策略可以增加局部尋優能力，而且在基本GWO 中，它充分考慮到的是局部尋優，尋找每一次的最優解，通過差值剔除策略的加入形成的GWO-DE 則是在全局尋優能力上有所提升。為了更加直觀顯示改進算法的有效性，將GWO-DE 在函數30維的情況下，分別對10 個測試函數進行尋優，如圖2 選取了其中6 個測試函數的尋優結果。從圖2 中可以看出，加入差值剔除策略的GWO-DE 尋優速度更快，求解精度更高，但對于Rastrigin函數尋優效果不明顯。

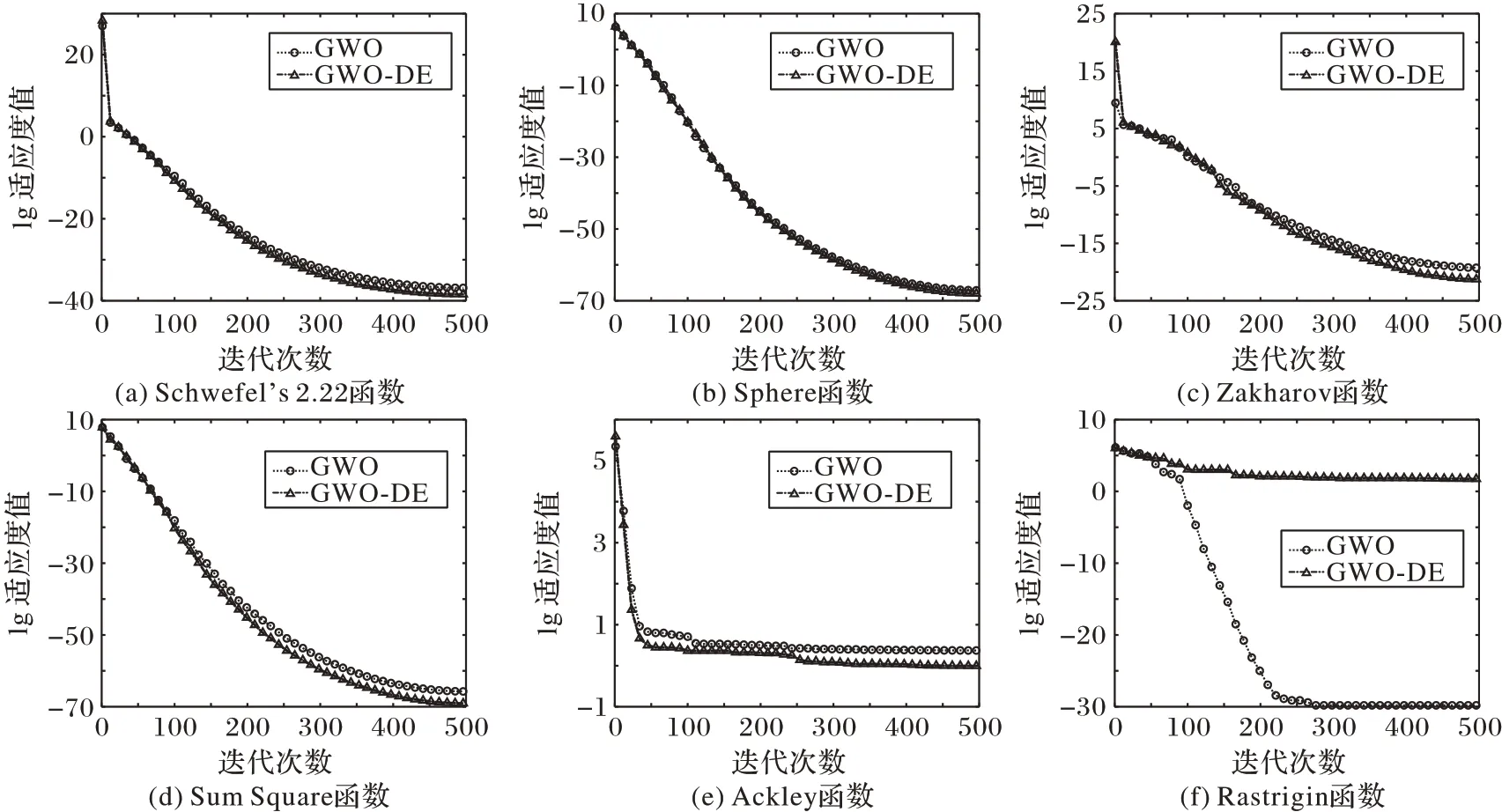
圖2 GWO與GWO-DE的尋優結果比較Fig.2 Comparison of optimization results of GWO and GWO-DE

4.3 IGWO仿真分析

為了比較的公平一致性，在實驗中基本GWO 和IGWO 采用相同的實驗參數和測試環境，可以從表2 的數據看出：IGWO 產生適應值的最優結果（Best）、最差結果（Worst）、平均結果（Mean）和方差結果（St.dev）都優于基本GWO 產生的結果，平均結果相比較說明在一定的迭代次數下IGWO 具有更快的收斂速度；10個函數的方差對比表明，IGWO 產生的方差更小，說明IGWO在每次的優化過程中穩定性和魯棒性更好。

為了更加直觀地反映算法的尋優效果，將基本GWO 與IGWO對6個測試函數的收斂曲線結果進行比對，如圖3所示。從圖3可以清晰地看出：對6個函數的測試中，無論是從收斂快 慢還是收斂精度上比較，IGWO都比基本GWO有所提高。

圖3 GWO和IGWO對6個函數的收斂性能比較Fig.3 Convergence performance comparison of GWO and IGWO for six functions

為了更加直觀看出IGWO的尋優性能，圖4選取了在單峰函數Sphere 與多峰函數Rastrigin 下，GWO、GWO-GPS、GWODE、IGWO 算法的尋優性能進行對比。通過仿真實驗可以看出，加入佳點集的初始化種群算法可以增強種群的遍歷性，在迭代前期可能效果不是特別明顯，但隨著迭代次數增加，GWO-GPS 的尋優性能就顯現出來了。再加入差值剔除策略來生成對等規模的新解，GWO-DE提高了收斂速度，可以幫助算法跳出局部最優。可見，IGWO 相比較GWO 更具有優越性，可以考慮把IGWO 運用到解決實際問題中，比如求解鐵路物流中心選址的問題上。

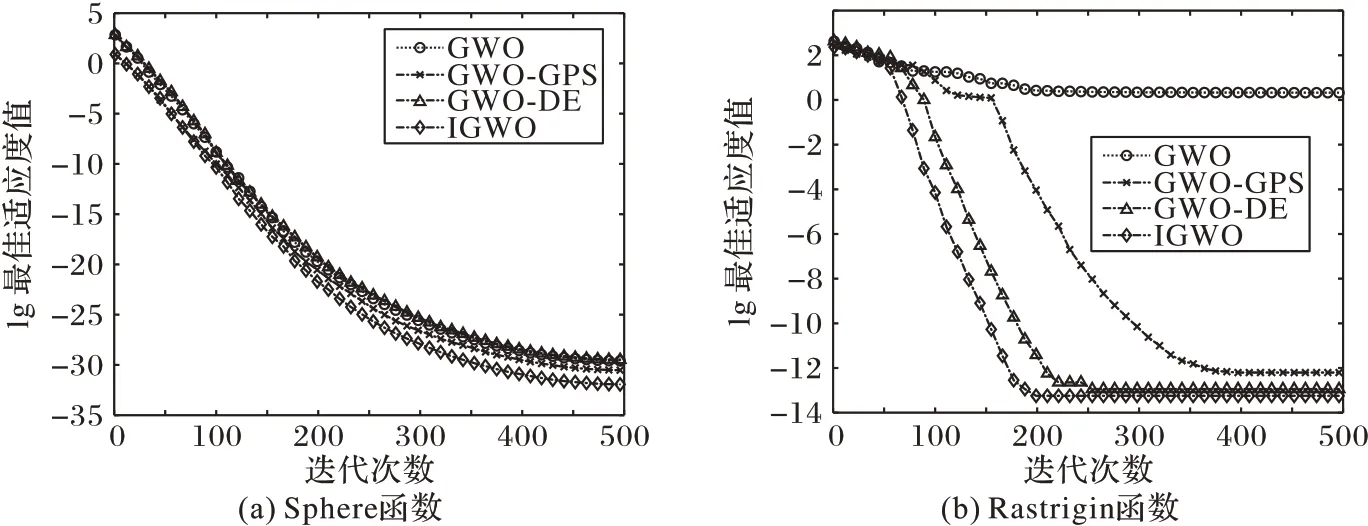
圖4 函數測試下GWO、GWO-GPS、GWO-DE、IGWO尋優性能對比Fig.4 Optimization performance comparison of GWO，GWO-GPS，GWO-DE，IGWO under function test

5 鐵路物流中心物流選址比對

為了驗證本文所提IGWO的優化可行性，本文獲取31個需要鐵路物流配送的城市地理位置信息，選取式（6）為目標函數，建立物流配送中心選址數學模型，并將IGWO與基本粒子群優化（Particle Swarm Optimization，PSO）算法、灰狼優化算法（Grey Wolf Optimizer，GWO）、差分進化（Differential Evolution，DE）算法與遺傳算法（GA）的迭代效果進行比對。假設31城市分別需要一個需求點，并從31個需求點中選出6個作為鐵路物流配送中心，其中地址的空間位置及需求量如表3所示。

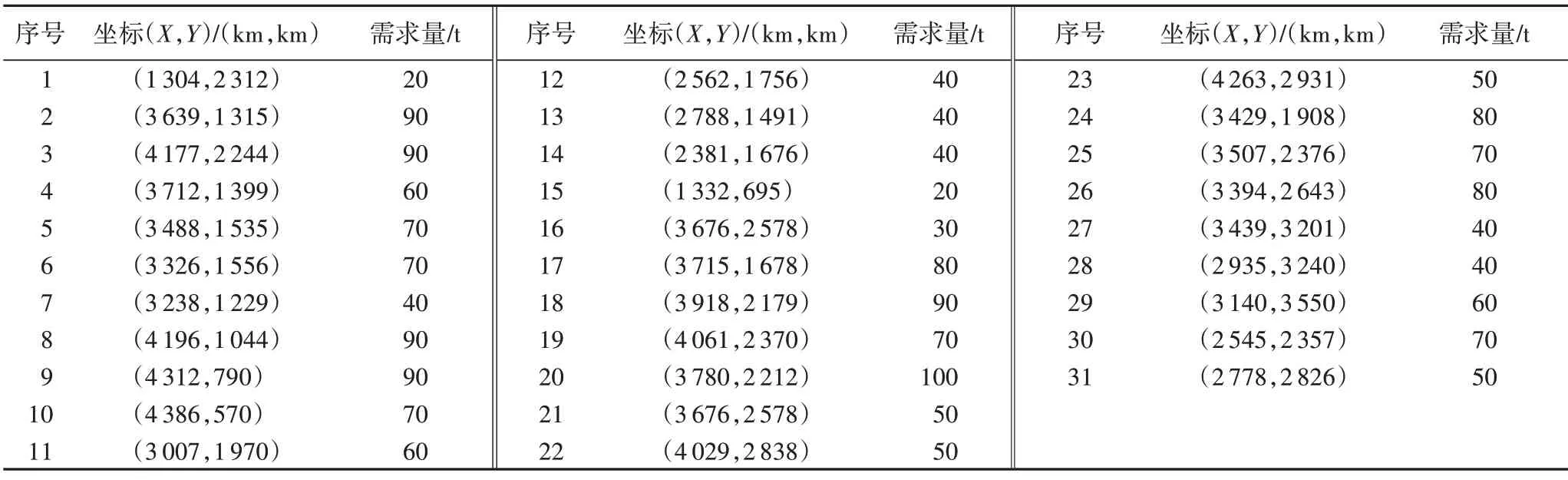
表3 用戶的位置與空間需求量Tab.3 Users’locations and space requirement amounts

圖5 分別展示了算法GWO 和IGWO 的鐵路物流中心選址，圖中所顯示的物流配送中心即為算法求得的最優解。

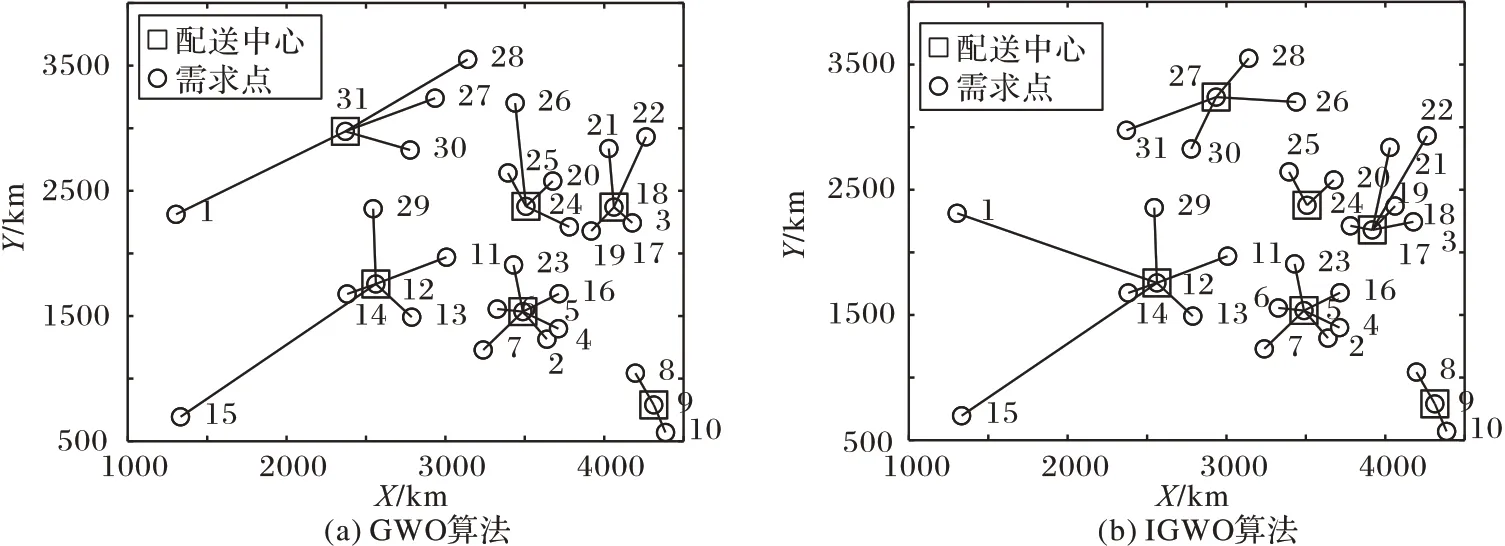
圖5 兩種算法選址結果對比Fig.5 Comparison of location selection results of two algorithms

以圖5（a）為例進行說明，配送中心31負責需求點26、27、28、30 的配送任務，配送中心24 負責需求點13、20、25 的配送任務，配送中心18 負責為需求點3、17、21、22 提供服務，配送中心12負責需求點1、11、13、14、15、29的配送服務，配送中心5 為需求點2、4、6、7、16、23 提供配送服務，配送中心10 為需求點8、9 提供配送服務。以此類推，圖5（b）展示IGWO 算法的選址方案，其中方框表示配送中心，圓點表示需求點，方框與圓點之間的連線表示某需求點的物資由物流配送中心負責配送。用本文所提改進灰狼優化算法對鐵路物流配送中心選址模型進行優化，得出的選址方案為［27，24，18，12，5，9］。

為了驗證IGWO在鐵路物流選址中的有效性，通過圖6對IGWO與其他四種基本智能算法適應度值進行對比。

圖6 五種算法迭代效果對比Fig.6 Comparison of iterative effects of five algorithms

從圖6 可以看出，在迭代前期IGWO 適應度值高于算法PSO、DE 與GA，隨著迭代次數的增加，IGWO 的全局尋優能力進一步增強，搜索與開發能力提高，IGWO 尋得的適應度值優于GWO 與GA。在整個迭代過程中，PSO 與DE 的穩定性更強，最終的尋優結果也略優于IGWO，但PSO 在迭代初期易陷于局部最優。還可以看出，在代數迭代的初期，GWO 最優值更穩定，但隨著迭代次數的增加，GWO 陷入了局部最優解，而IGWO 解決了這個問題，它從局部最優中跳出，增強了局部尋優能力，使得數據質量優于GWO。

從表4 可以看出，IGWO 尋優結果相較于GWO 提高了3.2%，IGWO 相較于PSO、DE、GA 運行速度分別提高了39.6%、46.5%、65.9%；IGWO 相較GWO 時間增加了5.6%，因為在GWO 中加入了差值剔除策略會導致再次生成與篩選種群的過程，消耗一定的時間，但尋優結果更加理想。雖然PSO 與DE 的適應度值更小，但它們的運行速度更慢。綜上所述，結合適應度值與運行速度整體綜合考慮，IGWO 優于大部分經典智能算法，有效減少了選址時間，全局搜索能力強，不易陷于局部最優，因此IGWO 求解鐵路物流配送中心選址問題求解得到的選址方案可以為實際的鐵路物流選址規劃提供一定程度的參考。

表4 5種算法的性能比較Tab.4 Performance comparison of five algorithms

6 結語

針對基本灰狼算法（GWO）求解鐵路物流配送中心的問題的局限性，本文提出了一種改進的灰狼優化算法（IGWO）。在GWO基礎上引入了佳點集來優化初始種群，使初始種群更加具有遍歷性，搜索能力加強。在基本灰狼算法位置更新中加入了差值剔除策略增加擾動因素，加快了收斂速度，有效避免了陷入局部最優，提高了局部尋優能力。

在對10 個標準測試函數的實驗仿真表明，本文提出的IGWO 有效提高了優化效率、收斂速度和魯棒性；然而，IGWO也有自身的局限性，對于某些測試函數實驗結果并不理想，可見IGWO 對于部分函數不適合。通過加入IGWO 優化鐵路物流選址模型，是對于求解鐵路物流中心選址的一種有效補充，可以有效降低運營成本。下一步研究可在模型的選取上進行優化，使IGWO 在物流選址問題或更多工業工程問題中有更深層次的優化性。