基于改進鯨魚優化算法的血液供應鏈網絡多目標魯棒優化設計

董 海，吳 瑤，齊新娜

（1.沈陽大學應用技術學院，沈陽 110044；2.沈陽大學機械工程學院，沈陽 110044）

0 引言

2020 年新冠肺炎在全球蔓延，中國醫療隊及各有關部門的敏捷應對，為世界疫情治療贏得了寶貴時間。因此，在突發情況之時，如何更快、更好地完成各方面物資供應［1］，尤其是醫療物資供應成為了現階段學者們需關注的問題。血液供應作為醫療物資供應的一部分，也是生鮮供應的一種，其擁有與其他產品與眾不同的特點，例如：存儲時間短、需求預測難、中斷風險高、血型可兼容等。早期學者Nahmias［2］在研究時，就提出將血液作為生鮮易腐領域產品的想法；Gunpinar 等［3］針對血液產品中血小板和紅細胞的壽命很短的特點（1～3 d），提出了一個整數不確定條件下平衡計分卡的規劃公式，達到總成本最少的目標；Dillon 等［4］提出了一個考慮易腐性和需求的不確定性的兩階段規劃模型來設計紅細胞庫存政策；Zahiri等［5］考慮了血液供應鏈網絡的設計血型兼容性，建立了最小化總成本和最大化需求的雙目標優化函數；Heidari-Fathian等［6］提出了一種用于血液供應鏈設計的雙目標魯棒優化模型，旨在盡可能降低成本和碳排放；Diabat 等［7］將基于場景的雙目標魯棒優化應用于血液供應鏈，并考慮了隨機中斷的設施和路線進行優化。

易腐產品供應鏈網絡在設計時，國內外學者對于不確定因素的控制多采用模糊規劃、隨機規劃以及魯棒優化等方法。Zahiri等［8］提出了一種針對易逝品的供應鏈網絡模型，并應用魯棒方法控制其參數的不確定性；Darestani 等［9］考慮易腐貨物的排隊制度，對一個雙目標的閉環供應鏈網絡進行魯棒優化，并通過實驗驗證方法的有效性。對于更加脆弱的血液供應鏈網絡設計，學者們也多采用此類方法。Cheraghi 等［10］針對血液供應鏈網絡設計考慮了兩種血制品的制造方法，并利用魯棒優化方法來解決這一問題的不確定的需求；Ensafian等［11］又提出了一個隨機規劃模型來設計本地的血液供應鏈網絡，考慮到病人詳情給出了血小板的年齡和匹配規則；Rahmani［12］提出了一個動態魯棒的選址?分配模型，用于在災難情況下，在設施中斷風險和不確定性的情況下設計血液供應鏈網絡；Hosseini-Motlagh 等［13］開發了一種雙目標不確定性環境下的血細胞供應鏈網絡設計模型，目標為總成本最低，并采用隨機魯棒方法處理其不確定因素。魯棒優化方法是解決供應鏈網絡設計問題的有效方法。

血液供應鏈網絡設計問題是一個NP-hard 問題。近年來，學者多采用智能算法［13-14］解決此類問題。鯨魚優化算法（Whale Optimization Algorithm，WOA）是在2016 年由國外學者Mirjalili等［15］模擬鯨魚捕食方式開發的一種仿生物學算法，近幾年來，以其人工參數少、操作簡單的優勢，已應用于不少的大規模處理問題，如物流配送中心選址［16］和電網配置［17］等方面。但由于傳統WOA存在后期收斂速度慢、容易陷入局部最優的劣勢，有學者將其他算法與其結合［18］，改善其在運行過程中的缺陷。

綜上所述，現階段血液供應鏈網絡設計存在需求不確定、中斷風險等不確定因素，且在求解此類大規模問題時復雜性較高。因此，本文提出一個考慮安全庫存的血液制品供應鏈網絡設計多目標優化模型，并使用魯棒優化方法對不確定性因素進行處理，再通過ε-約束方法將多目標問題轉化為單一目標函數。針對上述模型，本文提出差分WOA（Differential WOA，DWOA）對其求解，并通過實驗驗證模型的有效性以及算法的優勢。

1 模型建立

1.1 問題描述

本文研究一個多層級、多周期、多產品的血液制品供應鏈網絡，如圖1所示。該網絡圖包含5個節點：血液捐助者D、當地血液中心B、移動采血車M、血液實驗中心L以及各醫院集合H。血液捐助者可以選擇附近的移動采血車或者當地血液中心進行捐贈，移動采血車將血液送到最近的當地血液中心或者血液實驗室。當地血液中心將從捐贈者或者移動采血車處收集的血液發送至血液實驗中心，血液實驗中心將血液進行分離處理，分離為白細胞、血漿、血小板等血液制品，分別按照不同標準存儲，再按照需求分別發放給各優先級醫院。

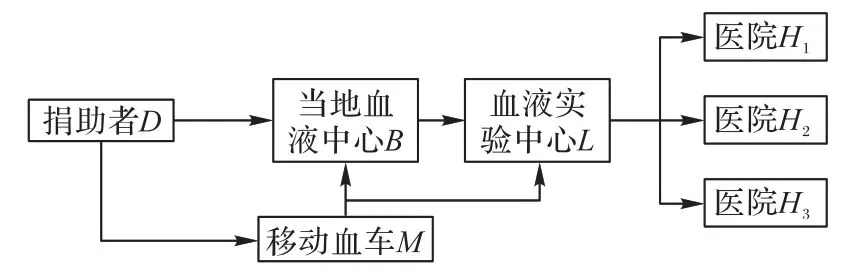
圖1 血液供應鏈網絡Fig.1 Blood supply chain network

1.2 模型假設及符號定義

本文假設如下：

1）移動采血車和當地血液中心的候選位置固定；2）各個采血點容量固定有限；3）假設各運輸過程均采用一種運輸方式；4）為避免收集階段血液過期，血液從采集到運輸至血液實驗中心時間小于8 h；5）未滿足需求將產生短缺費用；6）醫院庫存內額外的不同保質期的血制品作為安全庫存。

基于建模需要，定義符號如表1～3。

表1 符號定義Tab.1 Symbol definition

表2 參數定義Tab.2 Parameter definition

表3 決策變量Tab.3 Decision variables

1.3 模型建立

基于上述，本文建立如下模型：目標函數1 為最小化成本函數，目標函數2通過最小化血液中心l的存儲量來最小化時間。約束條件如式（3）～（31）所示。

目標函數1 最小化成本=建立成本+運輸成本+產出和持有成本+過期成本+需求不滿足成本+安全庫存成本

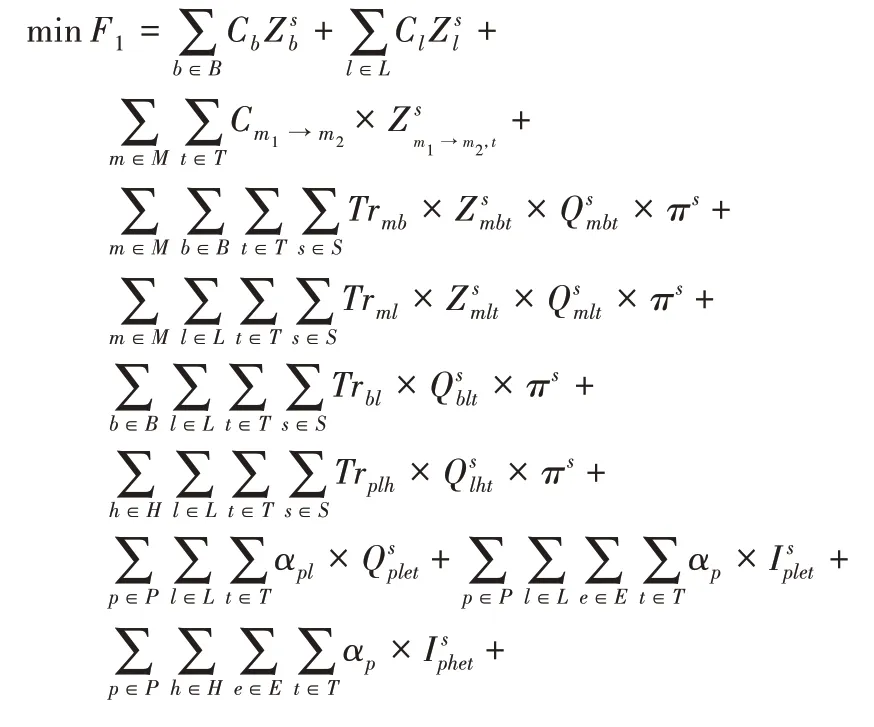
約束（3）表示每個周期最多只可以有1 個移動采血中心更換位置：

約束（4）表示移動采血中心的開放數量：

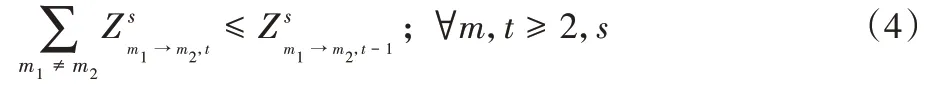
約束（5）表示每階段面向同一區域人群只有一個移動采血中心或者當地血液中心：

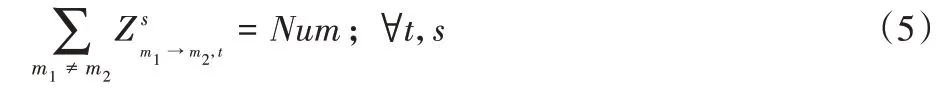
約束（6）表示捐贈者可以在移動采血中心和血液中心之間選一個進行獻血。

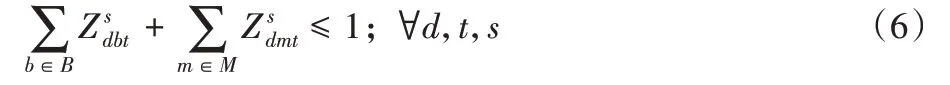
約束（7）、（8）、（9）表示移動采血中心和當地血液中心的覆蓋范圍：

約束（10）～（21）表示各節點及它們之間的流量、容量和庫存量限制：

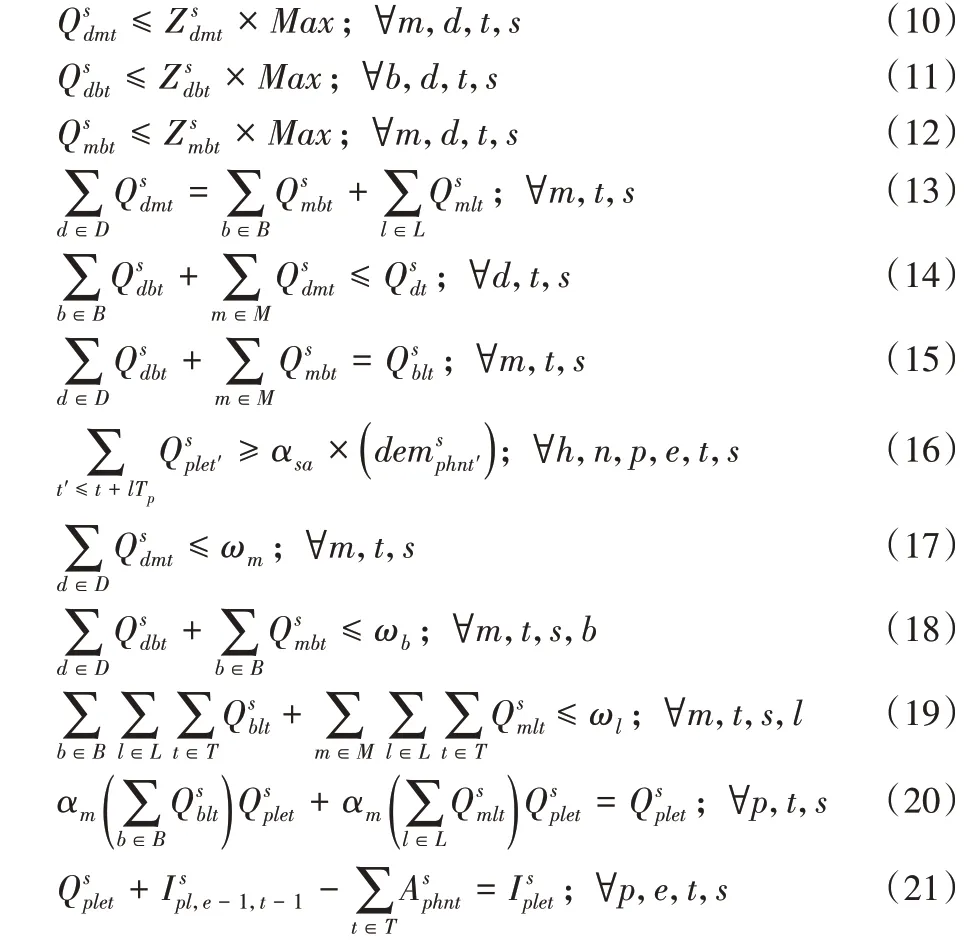
約束（22）和（23）分別表示產品需求量限制和過期限制：

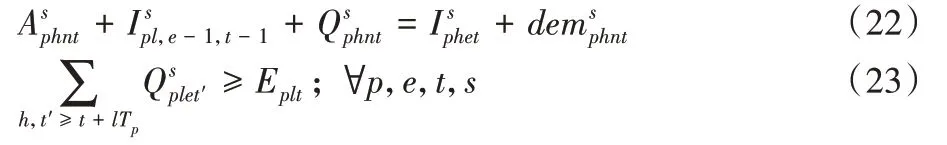
約束（24）、（25）表示未分配給優先級高的醫院之前不給低優先級的醫院配送：

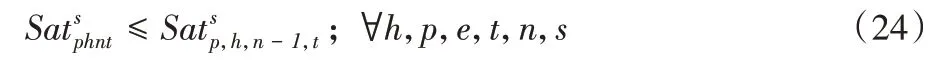
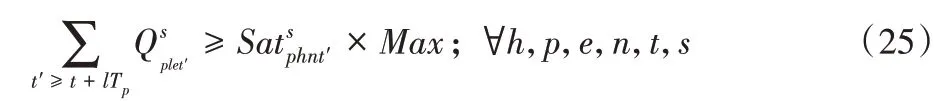
約束（26）、（27）表示血液實驗中心和醫院需求區的損耗：

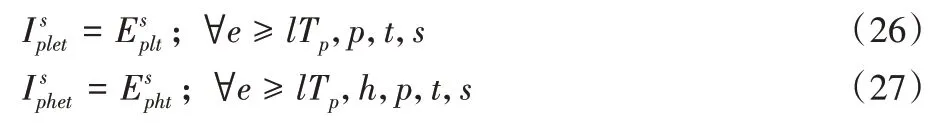
約束（28）、（29）保證血液實驗中心和醫院第一階段的初始庫存為0：

約束（30）、（31）表示決策變量的取值范圍：

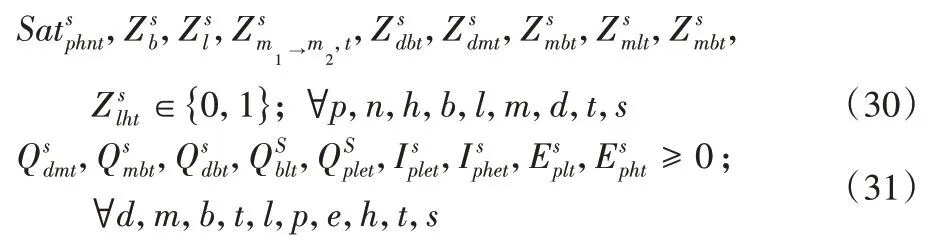
2 模型處理

2.1 多目標處理

隨著供應鏈網絡設計中需求增多，處理多目標問題成為近年來的熱點研究內容。求解此類問題一般采用標量、交互、模糊、元啟發式和決策輔助等方法。本文將采用ε-約束方法［19］對模型進行單一目標函數轉化。在應用ε-約束方法前，先對函數進行Pareto最優處理。Pareto最優的定義如下：

假設一個有“W”個目標的多目標函數定義如下：

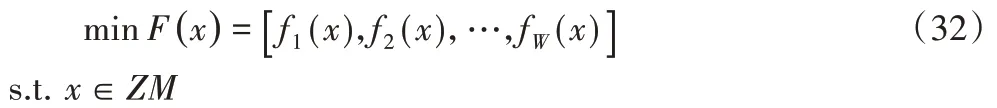
其中：X的集合ZM為問題的決策空間；f?(x)(?=1，2，…，W)為目標函數，W維函數稱為問題的目標空間。本文采用的ε-約束方法，處理細節為將其中一個目標函數最小化，其他目標附加為約束，具體如下：

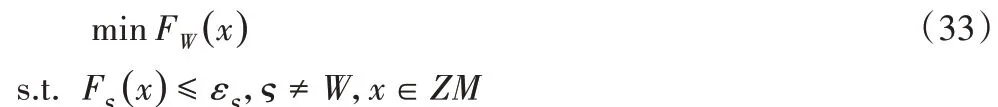
定理1每 個w∈{1，2，…，W}都ε?=F?x*，??∈{1，2，…，W}；x*∈ZM是一個約束條件下問題（32）的帕累托最優解。

定理2如果對于一些W，ε?=F?x*，??∈{1，2，…，W}，將x*∈X定義為一個在約束（34）下的問題（33）唯一解（對于一些W，ε?=F?x*，??∈{1，2，…，W}；x*∈ZM，其則為一個帕累托最優解。

定理3對于任何的上界向量ε={ε1，ε2，…，εW}，x*∈X，是問題（33）在約束下的一個帕累托最優解。

ε-約束方法在處理多目標優化問題方面，因其操作簡單，計算速度快，且具有很強的適用性，是一種非常有效的處理方法［20］。其主要思路是將其中一個更為重要或決策者更為偏好的目標作為目標，將其余目標轉換為約束條件，再進行求解。

本節用ε-約束方法對目標函數{F1，F2}進行處理。具體方法是將F1作為目標函數，F2被認為一個帶ε2的約束。因此，上文中的多目標模型可以轉化為以下單目標模型：

其他約束不變

2.2 魯棒處理

供應鏈網絡在真實設計中存在較多的不確定性，本文將使用魯棒優化方法［21］對上述模型進行處理。將發生概率為πs的不確定性場景的有限集合定義為s∈{1，2，…，S}，具體模型如下：

其中：成本函數是場景s∈S下的確定模型的最優值，成本函數是s∈S場景下發生的最優值。權重系數η和ρ是自由設定的兩個參數。

本文中移動采血車m，當地血液中心b和各節點間路線（當地血液實驗中心l和移動采血車m到當地血液中心b；當地血液中心b到當地血液實驗中心l；移動采血車m到當地血液實驗中心l的路線）是不確定的。根據以上描述，可得魯棒模型如下：

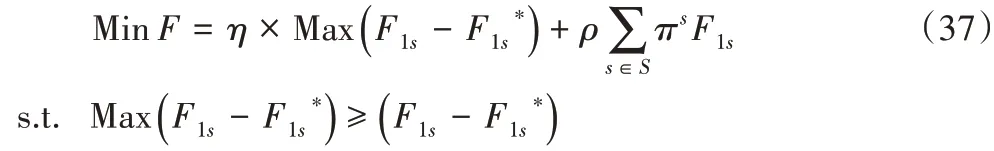
式(3)～(31)

其中：F1s和F1s*如式（38）、（39）所示：

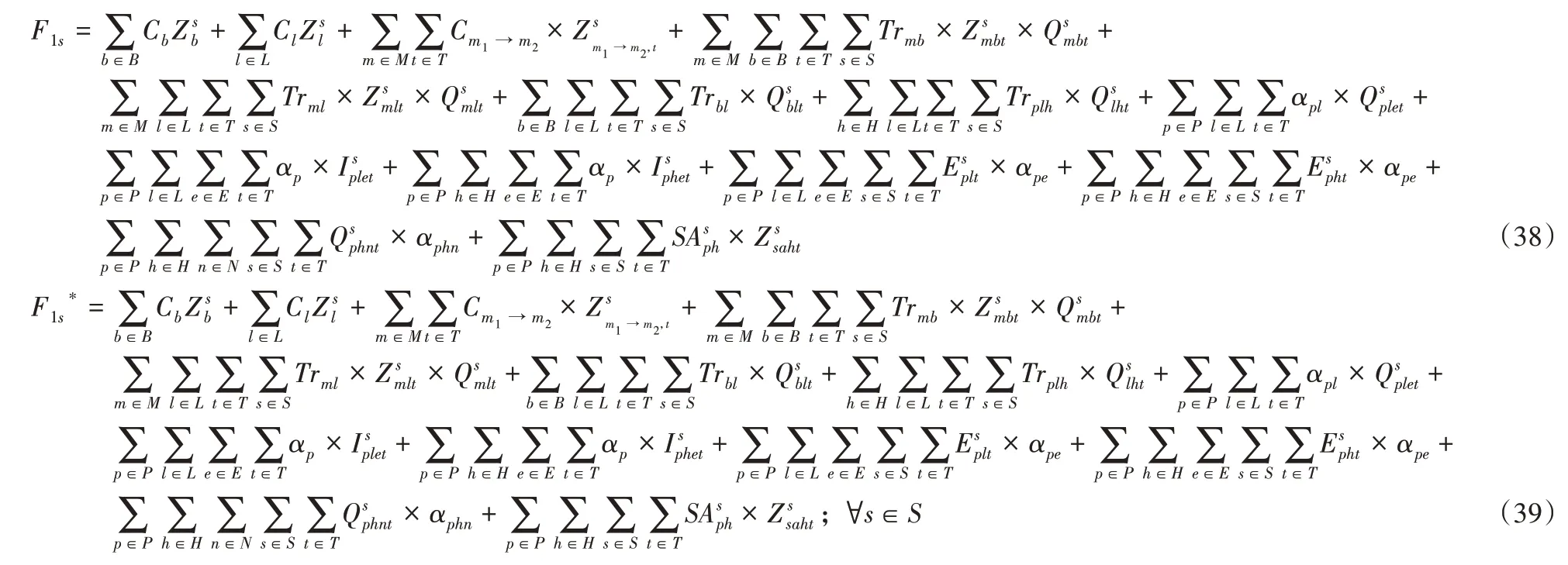
3 求解方法

3.1 原始鯨魚優化算法

WOA 的基本思想是通過模擬鯨魚獨特的捕食行為和社會行為來進行優化。以下為具體過程的數學模型。

3.1.1 包圍獵物

該階段選擇一個搜索代理，將其定義為前一代中的最佳解決方案。其他搜索代理試圖避開最優代理來實現全局搜索，具體描述如下：

其中：υ代表當前迭代次數；AW·DW是包圍步長；AW和CW是系數向量；XW(υ)是當前鯨魚位置向量；XW'(υ)是當前最優鯨魚位置向量；XW(υ+1)是每一次迭代中需要更新的最佳位置向量。系數向量AW和CW的計算如下：

其中：τ稱為收斂因子，其隨迭代次數增加從2 線性遞減到0；rand為區間［0，1］內的隨機數。τ的求解公式如下：

其中：υ為當前迭代次數；υmax是最大迭代次數。

3.1.2 泡沫網攻擊

鯨魚在捕食時通常采用螺旋運動的方式先包圍獵物，再進行捕獵。

在這一階段討論了兩種方法：收縮環和螺旋更新位置。收縮環的機制與全局搜索相似，并取值AW=[-1，1]；另一種方法是螺旋更新位置，根據當前位置和最優代理構造對數螺旋曲線，使得搜索代理逐步逼近最佳位置。具體描述如下：

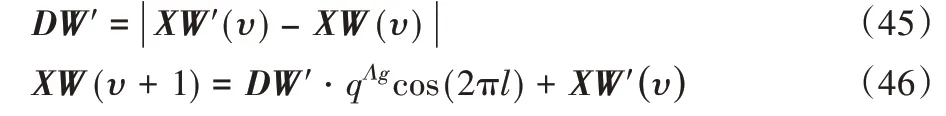
其中：DW'指當前鯨魚與最佳位置的距離，也就是獵物位置的向量；Λ為數螺旋形狀的常數量；g是區間[-1，1]內的隨機數；q為歐拉數，q=e。假設收縮包圍機制和螺旋位置更新概率相同，均為0.5。

3.1.3 搜索獵物

搜索獵物采取魚群隨機性位置更新的方法，數學模型如下：

其中：Xrand是隨機所得的位置向量。如果AW超出[-1，1]的范圍，就通過隨機尋找鯨魚個體，并根據個體的方位，排查其他鯨魚位置，面向全局搜索找到合適的獵物。

3.2 本文差分鯨魚優化算法

原始鯨魚優化算法存在著收斂精度低、收斂速度慢，以及容易陷入局部最優等缺點，而差分算法中的交叉和變異操作恰好因其全局搜索性強、性能更優，可彌補WOA 在這方面的劣勢。基于此，本文將差分算法的交叉變異方法應用到傳統鯨魚優化算法中，得到DWOA。利用差分算法中的變異策略替代WOA 中的隨機選擇策略，免去了參數D對于隨機搜索的影響；與此同時，在WOA進行隨機選擇新個體時，有效地利用了差分算法的交叉策略，使DWOA 搜索速度更快且種群更具多樣性。DWOA的具體策略如下。

變異策略：

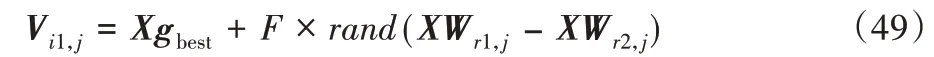
其中：Xgbest為當前種群最優位置；XWr1、XWr2為種群隨機個體；rand∈[0，1]；F為變異常數且F>0。

交叉策略：

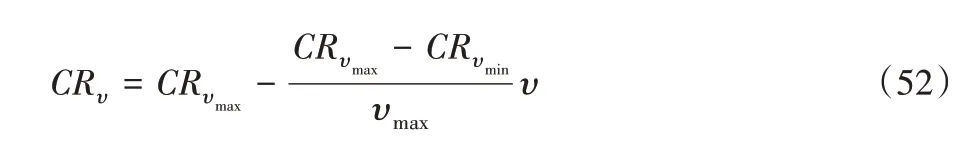
其中：υmin為最小迭代次數；CR為交叉概率；Fmax和Fmin分別為F的最大和最小值。

3.3 編碼處理

模型中決策變量只能取0-1，利用rand 函數和round 函數隨機取值0-1。供應鏈網絡設計問題的原始解為血液捐贈者起點到醫院客戶終點的運輸矩陣，再根據具體情況分配各種資源，確定優先級。因此，本文采用平均隨機數生成函數配合約束系數的方法，得到決策變量的值。在計算中，各個變量均采用實數編碼方法進行編碼。由d個捐助者、b個當地血液中心、i個血液實驗中心，m個移動采血車、h個醫院組成一條完整的編碼鏈，編碼長度為d+b+i+h+1，每條鏈均表示一條完整的血液供應鏈網絡生命周期內的運輸路徑。將個體適應度子集F編碼為群體中的解Xτ(τ=1，2，…，θ)，假定子集包含θ個個體適應度的值，即F=(F(ρ1)，F(ρ2)，…，F(ρθ))，若F(ρθ+1) ≥F(ρθ)，則F(ρθ+1)被選擇。

綜上所述，DWOA 的流程如圖2 所示，Y是用于確定選擇搜索環繞還是螺旋更新位置的因子。

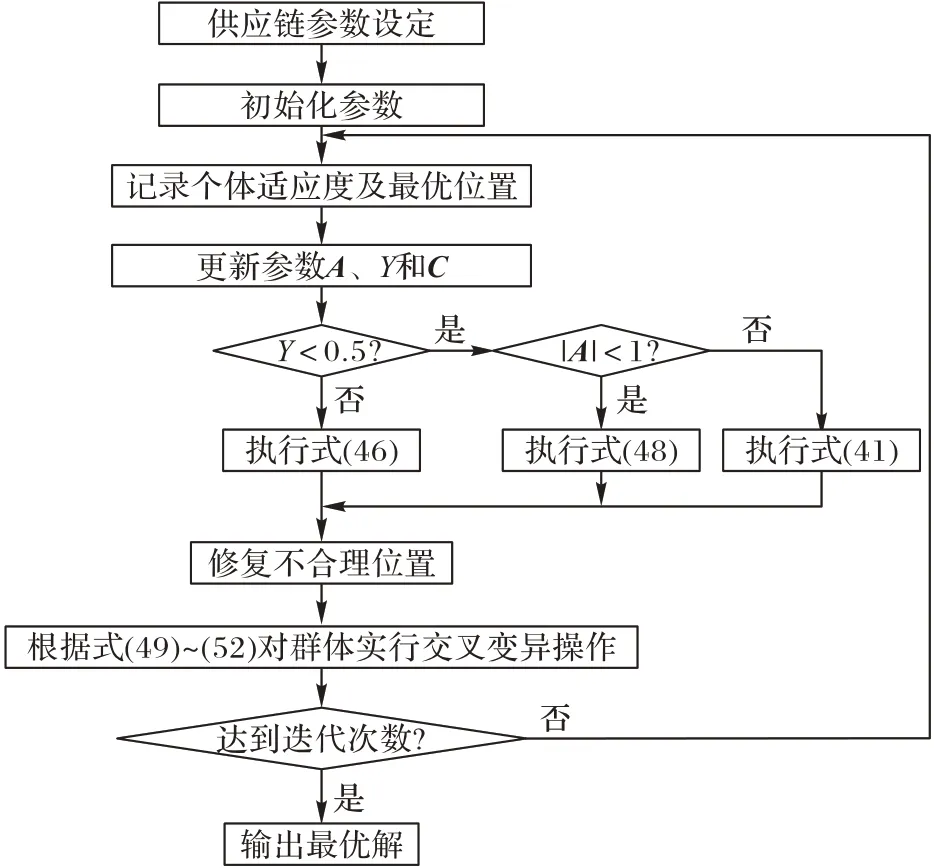
圖2 DWOA的流程Fig.2 Flowchart of DWOA

4 算例驗證

4.1 魯棒模型分析

為了分析魯棒模型的保守程度和擾動水平對于優化結果的影響，本節將針對表4 中的測試問題1、2，分別比較了相同擾動水平下，不同保守程度與不同擾動水平和相同保守程度兩種情況下，模型最優解和計算時間的數值，參數取值范圍如表5，結果如表6所示。

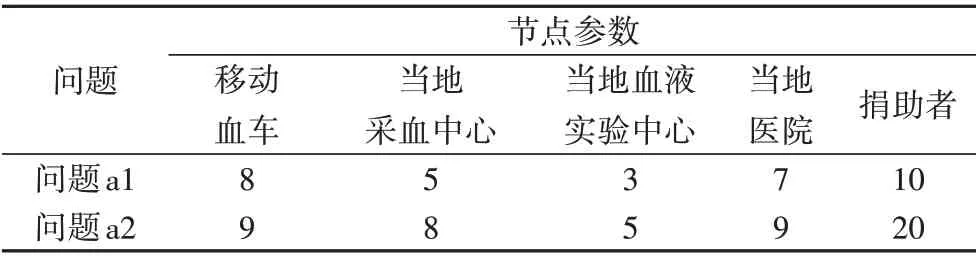
表4 測試問題aTab.4 Test question a

表5 參數范圍Tab.5 Parameter range

表6 不同擾動水平和保守程度下測試問題a分析Tab.6 Test question a analysis under different disturbance levels and conservation degrees

由此可知，血液供應鏈網絡設計存在不確定性時，總成本和總時間均大于各自確定性模型的預期值。隨著保守程度增加，總成本和時間都有所增加。也可以理解為，為應對不確定參數的擾動水平增加，需增加成本維持供應鏈網絡的穩定性。針對不同問題需求，保守程度和擾動程度存在一個最優值使得目標函數1、2 都是相對最優。與此同時，通過CPU 時間對比可知，一定范圍內，魯棒性能越強、越穩定，計算所需時間越短。

4.2 不確定性參數對模型影響

為了探究不確定性參數對于模型的影響，本節考慮其他參數一致的測試問題10 個（如表7），參數取值范圍如表5，得到結果如表8～9。

表7 測試問題b Tab.7 Test question b

表8表示隨著權重變化，目標函數（Z1、Z2）、ε-約束目標函數的變化。

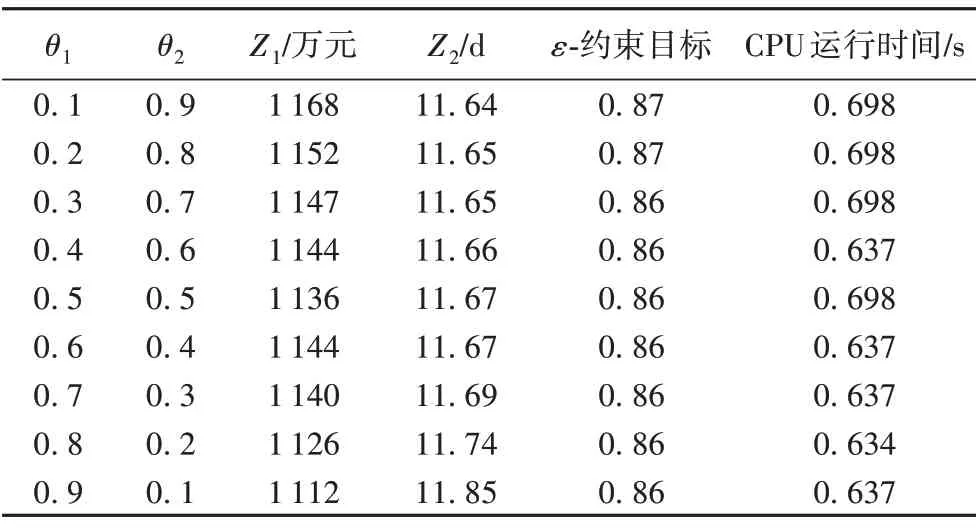
表8 不同權重下的函數最優值Tab.8 Optimal values of functions under different weights

表9 是針對隨機的10 個問題，魯棒模型和確定性模型對于需求的短缺的變化情況。

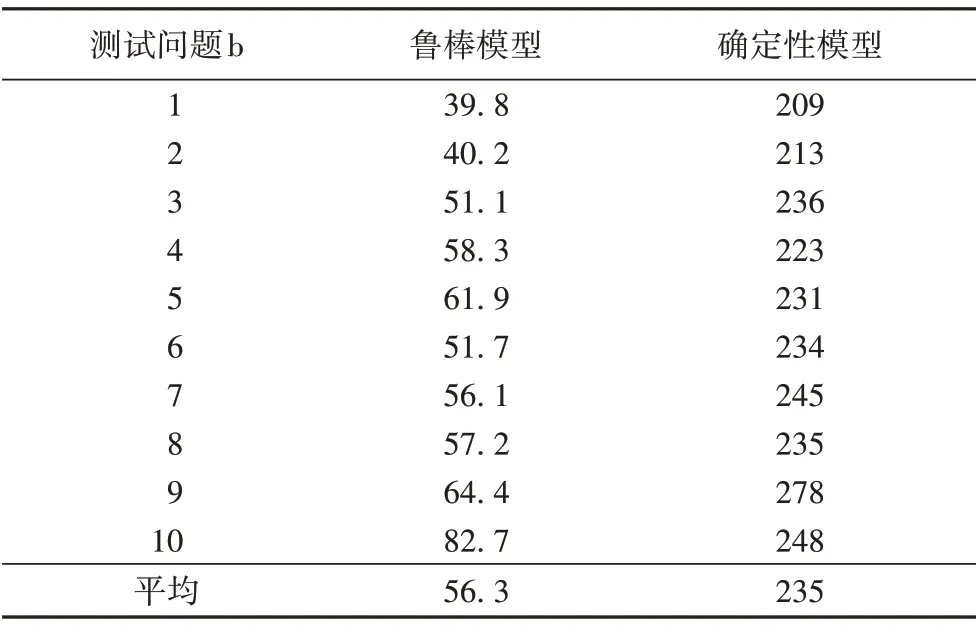
表9 需求不確定時魯棒模型與確定模型的需求短缺情況比較Tab.9 Comparison of demand shortages between robust model and deterministic model with uncertain demand

從表9 可知，魯棒模型相較于確定性模型在需求短缺方面有著絕對的優勢，短缺量平均減少76%，同時也體現出魯棒模型的穩定性。

4.3 算法性能測試

針對表4 的10 個隨機問題，本節利用Matlab 軟件對遺傳算法（Genetic Algorithm，GA）、原始鯨魚優化算法（WOA）、粒子群優化（Particle Swarm Optimization，PSO）算法和本文DWOA 進行對比分析，迭代500 次，四種算法對比分析如圖3所示。

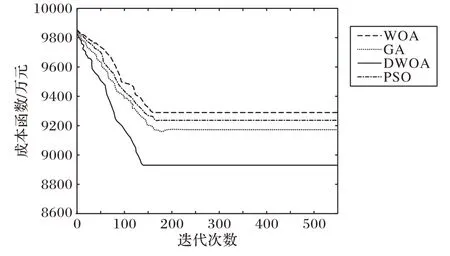
圖3 WOA、GA、PSO與DWOA算法成本的對比Fig.3 Cost comparison of WOA，GA，PSO and DWOA algorithms

由圖3 可知，DWOA 在求解問題時，相較于其他對比算法求解時間最短、目標值最優，更能擺脫局部最優。

WOA、GA與PSO算法相比各有優勢：WOA與PSO算法成本雖略高些，但可以更快搜索到最優解；GA雖收斂速度較慢，但求解成本更低一些，結果更優。

5 結語

針對血液供應鏈網絡設計的多目標魯棒優化問題，本文得出以下結論：

1）建立以成本最小、存儲時間最短的目標函數，并采用ε約束將雙目標函數轉化為單目標模型，使用魯棒優化方法處理不確定性，通過實例驗證，采用魯棒優化后的模型，取得結果更優，穩定性更強且處理時間更短。

2）采用DWOA 解決NP-hard 問題，并將該方法與WOA、PSO 算法和GA 進行對比，實驗結果表明，DWOA 計算時間較短，能夠較快跳出局部最優且穩定性強，在處理血液供應鏈網絡設計問題時，具有較好的優越性。

3）現實實際醫療中，血液分離后成分種類更為復雜，本文并未對不同種類（例如血漿、血小板）的血液制品保質時間、保存環境的不同進行深入分別研究，下一步的研究工作主要考慮血液制品種類多樣性以及不同血液制品要求的多樣性對于血液供應鏈網絡設計時的影響，以保證血液供應鏈網絡設計更加貼近現實醫療。