解析幾何教學中發展學生數學運算素養的思考

北京 相文明 王長友

每年高考的解析幾何綜合問題是牽動廣大師生敏感神經的重頭戲，此題既體現出命題者的立意對教學的導向引領，同時引導學生欣賞圓錐曲線優美的性質進而感悟解析法的無窮魅力，而解決此問題的基礎是學生的數學運算素養，因此在日常教學中教師必須系統思考、科學設計與規劃，進而實現發展學生的數學運算素養.

一、典型問題再現

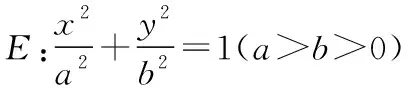
(Ⅰ)求橢圓E的標準方程；

(Ⅱ)過點P(0,-3)的直線l的斜率為k，交橢圓E于不同的兩點B,C，直線AB交y=-3于點M,直線AC交y=-3于點N，若|PM|+|PN|≤15時,求k的取值范圍.

(2)方法一：設直線l:y=kx-3，B(x1,y1),C(x2,y2),M(xM,-3),N(xN,-3),

(4+5k2)x2-30kx+25=0，400k2-400>0,

即k<-1或k>1,

且Δ=(30k)2-4×25(4+5k2)=400(k2-1)>0，

得|k|>1，

又由A,B,M三點共線得kAM=kAB，

因為|PM|+|PN|=|xM|+|xN|，

且顯然y1+2>0,y2+2>0，

又因為y1=kx1-3,y2=kx2-3分別代入，化簡得

化簡得|k|≤3,

所以k的取值范圍是[-3,-1)∪(1,3].

方法二：將原問題條件轉化為“過A作兩條直線AB,AC與橢圓交于B,C且滿足P,B,C三點共線”即可.

設直線AB的方程為y=mx-2，直線AC的方程為y=nx-2，易知m,n存在且m≠0,n≠0,m≠n.

設B(x1,y1),C(x1,y1),M(xM,-3),N(xN,-3),

又因為P,B,C三點共線，即kBP=kCP,

進一步化簡，并整理得25mn(m-n)-4(m-n)=0，

綜上，1<|kBC|≤3,所以k的取值范圍是[-3,-1)∪(1,3].

證明：設直線l:y=kx+m，A(x1,y1),B(x2,y2),P(x0,y0)，

(b2+a2k2)x2+2kma2x+a2(m2-b2)=0，

進一步整理(按照R的降冪排列)，得

變形整理，有[(kx0-(y0-m)][(λa2+b2)x0k+(λa2+b2)y0+(λa2-b2)m]=0,

顯然kx0+m-y0≠0(因為P?l)，所以(λa2+b2)x0k+(λa2+b2)y0+(λa2-b2)m=0,

再整理(b2-λa2)m=(λa2+b2)(kx0+y0).

①若x0=0，顯然y0≠0，說明直線l的斜率不存在，即直線l垂直于x軸;

(1)求C的方程；

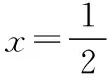
(1)因為|MF1|-|MF2|=2，所以軌跡C為雙曲線右半支，c2=17，2a=2，

|TA|·|TB|=|TP|·|TQ|，

因為k1≠k2，所以k1+k2=0.

其他過程同方法一.

結合兩道高考試題及引申思考問題的特點，容易發現研究距離問題是解析幾何重要的考查內容，而解析幾何綜合問題中常見距離問題的刻畫均需要有較強的運算素養.在上述問題的解決中學生反饋的難點有三個：

需要按照k的降冪排列整理方程等.

結合命題考查特點與學生問題、難點說明，教師在教學中必須有效落實數學運算素養的培養.

二、教學思考

高考命題要體現“一核四層四翼”， “一核”是高考的核心功能，即“立德樹人、服務選才、引導教學”；“四層”為高考的考查內容，即“核心價值、學科素養、關鍵能力、必備知識”；“四翼”為高考的考查要求，即“基礎性、綜合性、應用性、創新性”.解析幾何的綜合問題是優良的考查載體，而數學運算素養恰恰是基礎與關鍵，這就要求教師要不斷主動思考，一方面教師對數學運算素養的理解站位要高，另一方面教師要落腳更實，合理規劃數學運算素養的培養路徑，引導學生在學習過程中內化.

(一)解析幾何中數學運算素養的理解

1.課標要求

數學運算是指“在明晰運算對象的基礎上，依據運算法則解決數學問題的素養.主要包括：理解運算對象，掌握運算法則，研究運算思路，選擇運算方法，設計運算程序，求得運算結果”.

結合解析幾何的研究特征即“借助幾何圖形特點，形成解決問題思路，通過直觀想象和代數運算得到結果”，數學運算既是研究的方法又是檢驗學生運算素養水平效果的基石.

2.解析幾何中運算素養的基本層次理解

解析幾何教學中要重點關注“理解運算對象、研究運算思路、選擇運算方法”三個角度，學生數學運算素養的落實要體現差異性、層次性，是教師主動指導與設計培養的螺旋式上升的實施過程.教學中，教師一方面理解學生即學生的個體差異是客觀事實，另一方面要把數學運算分解為有針對性、具體性、操作性的目標.

3.整體把握教材內容設計中要求的數學運算素養

教學內容是直線與方程、圓與方程、圓錐曲線與方程三個層面設計，基本邏輯是由易到難、由直觀到抽象、由經驗到理性的學習過程.其中體現的運算要求為直線與圓的章節側重能用代數方法運算處理問題并體會運算的合理選擇、準確操作等；圓錐曲線側重理性思考運算的對象、運算的策略與思路、運算的方法與求解，要求學生養成準確、合理、簡潔、迅速的運算習慣，并能體會數學運算在解決數學問題中的價值.

(二)解析幾何中落實數學運算素養的策略與方法思考

解析幾何的問題幾乎處處離不開運算，學生的運算素養直接制約著教學目標是否實現，教師在教學中要明確基本的運算素養培養策略.

1.以數學邏輯推理為根本指導運算素養

章建躍先生認為：數學學習的基本任務是學會運算和推理，運算離不開推理，推理在高中乃至整個基礎教育階段的數學學習中的展現形式就是運算.會推理才能運算是基本共識，而具體在解析幾何教學中，就是要讓學生明白“研究對象是誰？研究對象間的關系如何刻畫？為什么要合理選擇代數關系刻畫圖形特征？運算的目標與方向是什么？達成的路徑是否準確與合理？”等基本問題.

教師要充分意識到邏輯推理是產生運算的思維基礎，學生只有條理清晰才能在運算的算法操作中明方向、懂算理.解析幾何綜合問題的邏輯基礎是參數選擇的準確性(能否用參數串聯表述問題)、合理性(算法是否簡潔)，重點是條件與結論的合理翻譯轉化，標準就是數學運算的可行性、操作程序的簡便性.

2.以算法為依托主動分析運算的效能

解析幾何研究的運算對象較多，教學需要引導學生從關系入手，尋找連接點，合理設計或構造運算程序與選擇運算方法，即“算什么？怎么算”.

(1)建立算法整體觀

解析幾何的問題更多是選擇合理參數，以“設而不求、尋找聯系”為出發點與落腳點，養成整體算法思考是學生必須掌握的技能.基本算法的共性是明確運算對象的方向、厘清運算的途徑與關系即整體考慮算法，重點關注運算過程中的方程本質，明確代數變形中的“主元與結構特征”.

(2)明確運算方向優化算法

運算方向決定運算程序，解析幾何問題要引導學生首先分析、思考運算的方向，進而確定運算目標與運算方法，本質是數學簡潔美的體現.

(3)掌握運算策略簡化算法

解析幾何運算策略的重要體現：一為定性與定量的結合，關注定性明方向，關注定量求準確；二是要時刻進行化繁為簡；三是整體代換重視運算結構.

3.以幾何性質為線索實現運算的優化

解析幾何的本質是用代數方法研究幾何問題，自然而然解決問題中要關注幾何圖形的性質與特征，熟練學會合理挖掘幾何性質簡化運算量.

4.以常規運算為載體逐步提升運算素養

解析幾何與運算形影不離，教師要分階段、分層次的設計實施.從數字的計算到字母的運算、從代數式的化簡到距離、角、位置關系等基本量的代數刻畫與求解、從簡單模仿到主動思辨、從關注運算結果到探究運算思路(包括分析運算條件、探究運算方向、選擇運算方法、設計運算程序)等.

5.以學生的意志品質為生長點實現運算素養的落實

學生運算素養的提升是最終的目的，學生的主動性與個性品質是關鍵，教師教學中要關注學生的認識、理解與感悟.一方面，教師要設計不同情境問題與學習方式激發學生需求與內驅力，讓學生想做；另一方面，教師要差異化設計與積極評價學生的進步與增長點，讓學生有成就；第三方面，教師要高位引領，給學生具體有效的指導，讓學生有收獲.