以問題解決之“形”，促思維生長之“神”——淺談習(xí)題處理的幾點(diǎn)看法

江蘇省無錫市江陰市夏港實(shí)驗(yàn)小學(xué) 繆美媛

“在問題解決后繼續(xù)前進(jìn)”不僅能夠充分發(fā)掘習(xí)題的價(jià)值，更能有效提升學(xué)生的思維。但是在實(shí)際教學(xué)中，很多教師對這一點(diǎn)的認(rèn)識遠(yuǎn)遠(yuǎn)不夠，在處理習(xí)題時(shí)，往往只滿足于學(xué)生獲得正確的答案。

數(shù)學(xué)教育家波利亞說過：“即使相當(dāng)好的學(xué)生，找到問題的答案并寫出漂亮的答句之后，就合上書本找點(diǎn)別的事情來做，這樣他們就失去了一次自我提升絕佳機(jī)會(huì)。” 確實(shí)如此，很多情況下，學(xué)生在問題解決的過程中，會(huì)帶來一些零散的、模糊的、感性的認(rèn)識，但“問題解決”的能力并沒有獲得相應(yīng)的提升。因此，在問題解決之后繼續(xù)前進(jìn)，不僅僅是為了鞏固學(xué)生原有的認(rèn)識，更重要的是使學(xué)生獲取更一般的策略，形成新的認(rèn)知，有效地發(fā)展數(shù)學(xué)思維。

一、進(jìn)行恰當(dāng)追問，深化原有的知識結(jié)構(gòu)

數(shù)學(xué)問題解決的過程往往伴隨著對數(shù)的概念抽象和數(shù)量關(guān)系的建構(gòu)。在解決問題的過程中，學(xué)生并不一定都是進(jìn)行理性思考，很多時(shí)候依賴的是直覺和對例題的簡單模仿。如果教師能夠在學(xué)生解決問題之后，適時(shí)適當(dāng)?shù)刈穯枺蚜?xí)題和本節(jié)課的學(xué)習(xí)內(nèi)容相結(jié)合，讓學(xué)生不斷地思考、交流，學(xué)生就會(huì)在思考的過程中，深化對原有知識結(jié)構(gòu)的認(rèn)知。

在蘇教版數(shù)學(xué)三年級下冊“認(rèn)識分?jǐn)?shù)”的教學(xué)中，筆者設(shè)計(jì)了3個(gè)核心問題，讓學(xué)生自主探索：

第一個(gè)問題：“8個(gè)桃子平均分成4份，每份是幾分之幾？”（如圖1）學(xué)生下意識地得到了“”三種不同的答案，產(chǎn)生這樣的疑惑和分歧是在筆者意料之中的。學(xué)生形成認(rèn)知上的沖突，就會(huì)迫不及待地想通過動(dòng)手操作來驗(yàn)證，并在操作驗(yàn)證中明確解決問題的方法。經(jīng)過操作，學(xué)生進(jìn)一步清晰地感知了“一個(gè)整體”的含義。

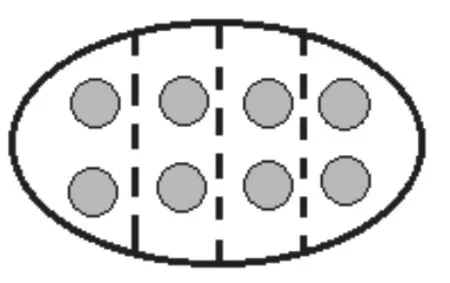
圖1

圖2

圖3

二、回顧解題過程，提升解決問題的水平

弗賴登塔爾認(rèn)為，數(shù)學(xué)的發(fā)現(xiàn)來自直覺，而分析直覺理解的原因是通向證明的道路。這就是說：學(xué)生在問題解決的過程中獲得的經(jīng)驗(yàn)，必須借助回顧反思，才能有意識地思考問題解決背后潛藏的數(shù)學(xué)實(shí)質(zhì)，學(xué)生的思維才能真正深入到數(shù)學(xué)化的過程之中，才能有效地提高學(xué)生問題解決的水平。

基于課標(biāo)“四基”的要求，在三年級下冊《長方形和正方形的面積計(jì)算》這節(jié)課的設(shè)計(jì)時(shí)，筆者著重思考了以下兩個(gè)問題：

（1）長、正方形面積計(jì)算公式的獲得，學(xué)生該經(jīng)歷怎樣的學(xué)習(xí)過程？

公式的背后，濃縮了一系列的操作推理過程。是讓學(xué)生實(shí)際測量后歸納和驗(yàn)證，還是引導(dǎo)其逐步深入地操作、想象、推理、歸納？毋庸置疑，體驗(yàn)的深刻必然促進(jìn)理解的深入。基于此，在充分把握了長方形面積公式本質(zhì)的基礎(chǔ)上，依據(jù)學(xué)情，本節(jié)課精心設(shè)計(jì)了難度漸增的三個(gè)層次的探索活動(dòng)，引導(dǎo)學(xué)生主動(dòng)探索、自主發(fā)現(xiàn)面積公式：第一層次，同桌合作用1cm2的小正方形直接測量1號長方形的面積；第二層次，1個(gè)小正方形都不能用，測量出2號長方形面積；第三層次，想象計(jì)算，逐步抽象出長方形的面積公式。

（2）除了收獲一個(gè)計(jì)算公式，這節(jié)課學(xué)生還能收獲些什么？

公式的獲得當(dāng)然是本節(jié)課的主要目標(biāo)，但是，教學(xué)也不能僅僅止步于知識技能的習(xí)得。除此之外，我們還能給學(xué)生些什么？結(jié)合公式的探索過程，通過幾個(gè)小環(huán)節(jié)的引導(dǎo)梳理，本節(jié)課，還著力讓學(xué)生感受了“簡單入手—發(fā)現(xiàn)規(guī)律—總結(jié)方法”這一數(shù)學(xué)問題解決方法，從而為學(xué)生今后的學(xué)習(xí)埋下研究的“種子”，長方形的面積計(jì)算成了學(xué)生后續(xù)學(xué)習(xí)中知識和方法上的雙重“跳板”。

基于以上思考，在課末，筆者引導(dǎo)學(xué)生反思：“這節(jié)課你有什么收獲？”學(xué)生們紛紛發(fā)表觀點(diǎn)。一個(gè)學(xué)生說：“我學(xué)會(huì)了求長方形和正方形的面積方法，長方形的面積=長×寬，正方形的面積=邊長×邊長。”另一個(gè)學(xué)生說：“我不僅學(xué)會(huì)了怎么計(jì)算面積，我還知道了研究問題，可以從簡單的開始。”還有一個(gè)學(xué)生說：“我知道了研究問題要多找?guī)讉€(gè)例子，經(jīng)過觀察、實(shí)驗(yàn)、數(shù)據(jù)分析和思考，就能找到里面的奧秘。”……雖然學(xué)生的語言是稚嫩的，但是思考卻越來越深刻了。今后，學(xué)生再遇到此類問題，就可以進(jìn)行方法和思想的遷移，這種能力具有生長力，學(xué)生解決問題的能力在回顧中獲得了實(shí)實(shí)在在的提高。

三、反思解題結(jié)果，優(yōu)化解決問題的策略

學(xué)生的探究呈現(xiàn)出不同的結(jié)果，這就反映出學(xué)生思維水平的不同。教師既要關(guān)注結(jié)果的正確與否，更要借助結(jié)果的表達(dá)，透視學(xué)生的思維，進(jìn)而提升學(xué)生的思維，優(yōu)化解決問題的策略。

學(xué)生在認(rèn)識了因數(shù)和倍數(shù)后，接下來就要研究一個(gè)數(shù)的因數(shù)和倍數(shù)。筆者出示例題：寫出36的所有因數(shù)。

首先放手讓學(xué)生嘗試去寫，在巡視時(shí)有意識地尋找學(xué)生的答案。在交流反饋中呈現(xiàn)學(xué)生三種不同寫法：

（1）36的因數(shù)有：3，9，12，6，4，36，1；

（2）36的因數(shù)有：1，36，2，18，3，12，4，9，6；

（3）36的因數(shù)有：1，2，3，4，6，9，12，18，36。

然后把三份學(xué)習(xí)單的答案放在投影上，問：“你知道三位同學(xué)是怎樣想的嗎？”讓所有學(xué)生一起反思他們的思考。在交流中學(xué)生逐漸認(rèn)識到：第一種方法是想到一個(gè)寫一個(gè)，思維比較亂，這樣容易遺漏；第二種方法是一對一對地找，先想1×幾，再想2×幾，接著3×幾，找的時(shí)候還很有順序，這樣就不會(huì)遺漏；第三種方法也是一對一對地尋找，但它比第二種方法更好，好在寫完后，所有的因數(shù)是按從小到大的順序排列的，是怎么做到的呢？原來是在寫的時(shí)候一前一后，這樣就排成了一組從小到大排列的數(shù)，顯得更加有序。在這樣的反思中，學(xué)生逐步形成了“成對尋找”“分組書寫”“有序思考”的策略。

四、分析錯(cuò)誤原因，生成新的教學(xué)資源

在學(xué)習(xí)的過程中，學(xué)生犯錯(cuò)誤是在所難免的。犯錯(cuò)并不是一件壞事，一些典型的錯(cuò)誤如果能夠及時(shí)地捕捉，反而會(huì)成為非常好的教學(xué)資源，讓課堂有“生成”的精彩，并起到防微杜漸的作用。因此，在課堂教學(xué)中，教師要鼓勵(lì)學(xué)生真實(shí)地表達(dá)自己的想法，并引導(dǎo)其他學(xué)生共同分析錯(cuò)誤的原因。

教學(xué)蘇教版數(shù)學(xué)四年級下冊《軸對稱圖形》一課時(shí)，筆者呈現(xiàn)了長方形、正方形、平行四邊形、圓，一起探究這些平面圖形是不是軸對稱圖形。在研究到平行四邊形時(shí)，學(xué)生產(chǎn)生了分歧：大部分學(xué)生認(rèn)為平行四邊形是軸對稱圖形，只有極少學(xué)生則認(rèn)為平行四邊形不是軸對稱圖形。

隨即，筆者問：“口說無憑，你怎么說服同學(xué)？”這時(shí)，一個(gè)學(xué)生拿出一個(gè)平行四邊形，通過對折說明了平行四邊形不是軸對稱圖形。其他學(xué)生仍有疑問：“換個(gè)方向再對折也許可以重合。”于是，學(xué)生們嘗試了將平行四邊形朝多個(gè)方向?qū)φ郏l(fā)現(xiàn)仍然不能完全重合，這才形成了一致的結(jié)論：平行四邊形不是軸對稱圖形。

而筆者卻沒有就此止步，而是引導(dǎo)全班學(xué)生思考：“為什么剛才很多同學(xué)會(huì)把平行四邊形誤認(rèn)為是軸對稱圖形？”學(xué)生反思自己的思考，有的說：“因?yàn)槲覜]有操作，是憑感覺的。”有的說：“沿對角線對折，兩邊的形狀和大小完全相同。”還有的說：“沿對角線對折，感覺會(huì)重合。”筆者接著說：“從剛才這些同學(xué)的回答中，你得到了什么啟示？”學(xué)生紛紛舉手發(fā)言，有的說“判斷一個(gè)圖形是不是軸對稱圖形，不能憑感覺，而要借助對折，看一看對折后兩邊的圖形能不能完全重合。”有的說：“即使對折后兩邊的圖形形狀、大小都相同，也不一定是軸對稱圖形。”還有的說：“很多圖形看起來像軸對稱圖形，但不一定是。”“數(shù)學(xué)不能憑感覺做出判斷，而要真正深入地去思考。”……由此可見，很多貌似粗心的錯(cuò)誤，如果做進(jìn)一步的分析，往往都能找到更深層次的原因，或是認(rèn)知層面的，或是思維層面的，或是心理層面的。教師有意地回避錯(cuò)誤或者無視錯(cuò)誤也就在無形中浪費(fèi)了一次絕佳的教育契機(jī)和一個(gè)絕好的教育資源。

綜上所述，筆者認(rèn)為數(shù)學(xué)教師絕不能滿足于在問題解決之后，只給學(xué)生一個(gè)正面的肯定，而要深入鉆研問題，挖掘問題蘊(yùn)含的教學(xué)價(jià)值，更要細(xì)致觀察學(xué)生的解答過程，準(zhǔn)確把握學(xué)生的思維水平，設(shè)計(jì)恰當(dāng)?shù)膯栴}，做出恰當(dāng)?shù)囊I(lǐng)，使每一個(gè)學(xué)生都能夠借問題解決之“形”，促思維生長之“神”。