楊輝三角在解決遺傳學問題中的妙用

>>>辛 波

本文通過對楊輝三角和數量遺傳的分析，找到了兩者之間的數學邏輯關系，進而提出解決數量遺傳題的新方法，為利用數學知識解決遺傳學問題提供了新思路。

一、楊輝三角的特點

楊輝三角，是二項式系數在三角形中的一種幾何排列，由我國南宋數學家楊輝于1261年在其所著的《詳解九章算法》中首先提出。在人教版八年級數學上冊中，我們已經接觸過楊輝三角。下圖即為楊輝三角：

圖1 楊輝三角

楊輝三角的內容有很多，本文主要用到下面幾點：

（1）每個數等于它上方兩數之和。

（2）每行數字左右對稱，由1 開始逐漸變大。

（3）第n 行的數字有n 項。

二、數量遺傳的特點

楊輝三角與遺傳學有什么關系呢？楊輝三角的數學特征與遺傳學中的數量遺傳有密切關系。高中生物課本中孟德爾遺傳定律所提到的性狀，例如豌豆的高莖和矮莖、圓粒和皺粒，在表現型上都顯示出質的差別，所以叫質量性狀。但是除了質量性狀外，生物體中還廣泛存在著另一類性狀差別，這些性狀的變異呈連續狀態，界限不清楚，不容易區分，叫做數量性狀。生物體的很多性狀，如玉米穗的長度、作物的產量、小麥種子的顏色等，都屬于數量性狀。數量性狀的遺傳雖然復雜，但本質上仍然屬于孟德爾遺傳定律的范疇，可以用多基因理論來解釋。數量遺傳的多基因理論主要包括以下三點：

（1）數量性狀受多對基因支配。

（2）這些基因對表現型影響小，相互獨立，但以積累的方式影響相同的表現型。

（3）每對基因均表現為不完全顯性，按孟德爾法則分離。

三、楊輝三角和數量遺傳的邏輯關系

上面給大家介紹了楊輝三角和數量遺傳的多基因理論，那么這兩者之間到底存在著怎樣的邏輯關系呢？下面通過一道例題來分析一下。

例1.小麥的粒色受兩對基因R1和r1、R2和r2控制，且獨立遺傳。R1和R2決定紅色，r1和r2決定白色，并有累加效應，所以麥粒的顏色隨R的增加而逐漸加深。將紅粒(R1R1R2R2)與白粒(r1r1r2r2)雜交得F1，F1自交得F2，則F2的表現型有 種，比例為 。

解析：根據題干中所給信息：R1和R2決定紅色，r1和r2決定白色，并有累加效應，麥粒的顏色隨R的增加而逐漸加深，這屬于數量遺傳。下面把F2的基因型和表現型詳細展示出來。

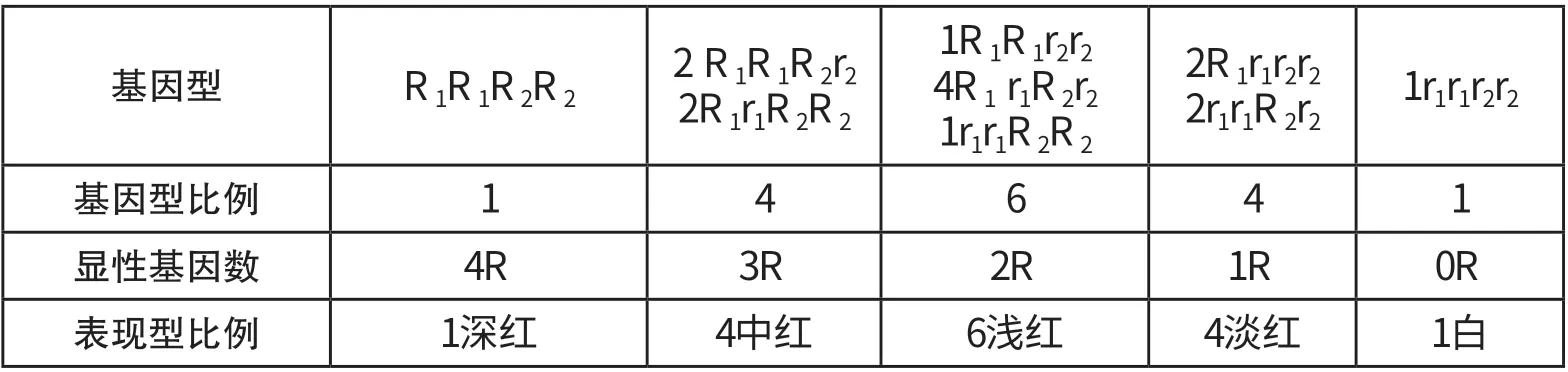
表1 兩對基因決定的小麥粒色的遺傳

從圖表中可以看出表現型有5 種，比例為1:4:6:4:1。那么這組數字有什么規律呢？通過與楊輝三角比較發現，這組數字就出現在了楊輝三角中，也就是說，兩對基因控制的數量遺傳對應的數字是楊輝三角中的1:4:6:4:1。那么，如果是由三對基因控制的數量遺傳與楊輝三角又有什么關系呢？我們繼續假設小麥的粒色是由三對等位基因R1r1R2r2R3r3控制，那么F2中顯性基因的數量和表現型的比例為：

表2 三對基因決定的小麥粒色的遺傳

我們把這組數字和楊輝三角比較發現，1:6:15:20:15:6:1 再次出現在了楊輝三角中，而且和剛才的1:4:6:4:1 正好隔了一行。通過比較這兩組數據可以發現這樣的規律：數量遺傳的數學特征是符合楊輝三角分布的，而且是取其單數行遺漏雙數行得到的。兩對基因控制的數量遺傳對應第5行，三對基因控制的數量遺傳對應第7 行，如果是四對基因控制的呢？答案是第9 行。其他以此類推。找到規律后，在解題中就可以直接使用了。

四、楊輝三角的應用

例2.(2014年上海生物卷，25題）某種植物果實重量由三對等位基因控制，這三對基因分別位于三對同源染色體上，對果實重量的增加效應相同且具疊加性。已知隱性純合子和顯性純合子果實重量分別為150g和270g。現將三對基因均雜合的兩植株雜交，F1中重量為190g的果實所占比例為（ ）。

A.3/64 B.5/64 C.12/64 D.15/64

解析1（傳統方法）：由于顯性純合子AABBCC 和隱性純合子aabbcc 果實重量分別為270g 和150g，所以每個顯性基因增重為20g，AaBbCc 果實重量為210g。F1中重量為190g 的果實基因型中含有兩個顯性基因和四個隱性基因，共有六種基因型：AAbbcc、aaBBcc、aabbCC、AaBbcc、AabbCc、aaBbCc。AAbbcc所占比例為1/4×1/4×1/4=1/64，同理aaBBcc和aabbCC均為1/64；AaBbcc所占比例為2/4×2/4×1/4=4/64，同理AabbCc 和aaBbCc 均為4/64；所以1/64×3+4/64×3=15/64。

解析2（楊輝三角法）：通過對題干分析我們發現，果實重量是受三對基因控制的數量遺傳，三對基因在楊輝三角中對應的數字是1:6:15:20:15:6:1，一共是64 份，190g 的個體含有兩個顯性基因，兩個顯性基因對應的數字是15，這樣我們就得到15/64。

通過這兩道例題我們展示了楊輝三角和數量遺傳的邏輯關系，而這種邏輯關系巧妙地解決了數量遺傳中的數學問題，提供了一種新的方法。利用楊輝三角來解決遺傳問題，相對于傳統方法而言計算量下降、準確度提高。數學中有很多知識可以用來解決生物問題，例如排列組合、二項式定理等。當然還有更多的數學知識等待大家去發掘，希望大家能多多研究，帶來更精彩的內容。