帶藥纏繞復合材料殼體張力分析及優化研究①

魯昊鉞，徐曉衛，鄭 慶，林天一，王林祥，江 真

(上海航天動力技術研究所，上海 201109)

0 引言

輕量化已成為高性能固體動力的發展趨勢之一，碳纖維增強復合材料(CFRP)因其高的比強度和比模量，已廣泛用在各類固體火箭發動機上[1-2]。其中，使用推進劑藥柱作為纏繞芯模，直接纏繞形成燃燒室殼體這一技術解決了推進劑澆注固化后與包覆層的脫粘問題，同時一體固化成型，減重效果明顯，具有十分巨大的發展潛力。該技術由歐洲推進技術協會(Societe Europeene De Propulsion，SEP)于20世紀80年代最先開始研究[3-5]。

帶藥纏繞技術中，張力制度至關重要。關于纏繞張力的研究，可概括為理論推導、仿真分析和實驗研究三大類。在理論推導過程中，丁寶庚等[6]分析了正在纏繞層施加的張力對已纏繞層張力的“放松效應”，建立了薄壁金屬內襯下的纏繞張力公式。SHIH等[7]建立了干法纏繞過程的力學模型，在纏繞層剩余張力的理論分析方面，大多數文獻使用彈性疊加原理進行計算。劉成旭等[8]針對柔性芯模提出了芯模徑向剛度的概念，為纏繞過程中剩余張力的理論計算提供了基礎。康超等[9]引入芯模徑向剛度后，基于各向異性纏繞層的彈性變形和厚壁筒理論，在彈性范圍內給出了纏繞層的徑向應力與環向應力。LIU等[10]基于線性熱粘彈本構模型，建立了考慮熱粘彈性效應的固化殘余應力分析模型，并利用所提出的工藝分析和優化模型，尋找最佳纏繞角度和纏繞張力。

纖維纏繞過程的有限元分析對結構設計和質量控制的意義重大。MANTELL等[11-12]建立了熱固性樹脂基復合材料纖維纏繞過程的仿真模型，將工藝變量(纏繞速度、張力、施加溫度)與制品的力學性能聯系起來。任明法等[13-15]根據含有金屬內襯纏繞成型制品在纏繞、固化和預超壓三個制造工藝過程中的特點，提出“溫度參數”法對纏繞過程進行仿真分析，提出等剩余張力的“迭代搜索法”張力制度設計。徐腸等[16]提出了利用“死活單元”模擬纖維纏繞過程的有限元數值計算方法，計算模擬實際纏繞過程。梁清波等[17]在引入芯模的徑向剛度系數基礎之上，結合了“溫度參數法”與“死活單元”法的優勢，將整體模型劃分為不同纏繞層，以溫度產生的收縮應力等效纏繞張力。

在實驗研究方面，WEI等[18]通過實驗探究了纏繞張力對纖維纏繞復合管彈性模量的影響。實驗結果表明，彈性模量隨纖維張力的增大而增大，纖維張力的影響不太顯著。汪洋等[19]通過不同張力單向板的拉伸和壓縮試驗發現，纏繞張力在60～80 N的區間范圍內，單層板的拉伸和壓縮性能較好。張曉軍等[20]給出了張力遞減的制度，可提高NOL環的拉伸性能。

本文對帶藥柱纏繞復合殼體使用的張力制度進行了研究，以纏繞層“剩余張力梯度”最小為目標，對張力制度進行優化，為帶藥柱纏繞復合殼體張力制度的設計及優化提供借鑒。

1 纏繞張力理論分析模型

固體推進劑屬于粘彈性材料，其力學性能同時是溫度和時間的函數，但纏繞過程與整個發動機的全生命周期相比可忽略。因此，認為纏繞過程中的藥柱芯模滿足虎克定律。在此基礎上，引入如下假設：

(1)除芯模重力外，纏繞過程中纖維層和藥柱芯模只受到纏繞張力產生的均勻外壓作用；

(2)纏繞過程中，藥柱芯模始終處于彈性范圍內；

(3)各纏繞層間緊密接觸，無任何的切向滑移，忽略摩擦力產生的影響；

(4)纏繞過程始終保持軸對稱性質。

本文所用藥柱芯模的物性參數見表1，張力作用的模型如圖1所示。

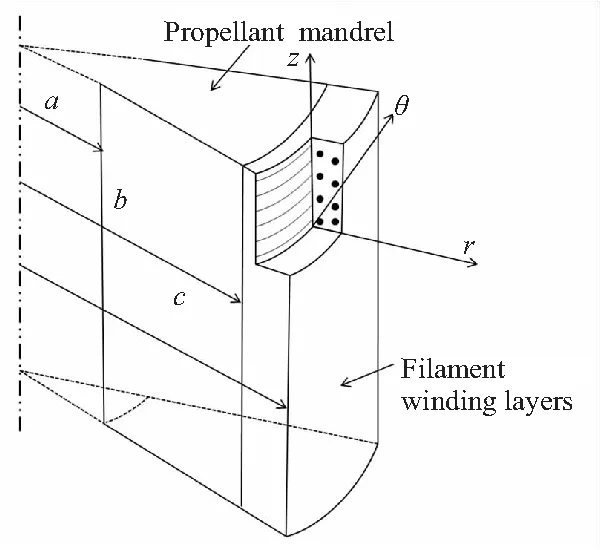
圖1 帶藥柱纏繞結構及張力作用模型

表1 藥柱芯模組件物性參數

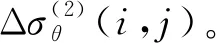
(1)

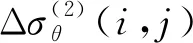
2 帶藥柱環向纏繞張力松弛分析

工程上鋼芯模常用的張力制度有恒張力模型、恒力矩模型及錐度張力模型。恒張力制度纏繞時，各層施加的張力一致，當前纏繞層會對已纏繞層的張力產生放松作用；恒力矩纏繞時，纏繞張力對芯模軸線的力矩是恒定的，隨著纏繞進行，纏繞半徑增大，張力減小，纏繞層出現“內緊外松”的現象；錐度張力模型是恒張力和恒力矩制度的線性疊加。這三種纏繞張力模型分別滿足以下關系[21]：

恒張力：

Tw(R)=T0

(2)

恒力矩：

(3)

錐度張力：

(4)

式中b為藥柱芯模外徑；R為正在纏繞層的半徑；T0為初始纏繞張力；α為錐度系數，α∈[0,1]。

本文試驗所用模擬藥柱芯模組件模量為30 MPa，通過單根纖維在藥柱芯模上纏繞的有限元仿真分析，初始纏繞張力在60 N時，對30 MPa模量的藥柱芯模組件影響較小。因此，取初始纏繞張力T0=60 N，藥柱芯模組件模量為30 MPa進行剩余張力分析。分別將恒張力、恒力矩及錐度張力公式代入式(1)，以60 N為初始纏繞張力作為輸入，錐度張力模型中的錐度系數α取0.95，以纏繞半徑為橫軸，剩余張力為縱軸，可做出不同張力制度下的剩余張力曲線，見圖2。可看到，當使用推進劑藥柱作為芯模后，纏繞層的剩余張力變化很大，對比不同張力制度下剩余張力的分布可以看到，恒張力制度與恒力矩制度下的剩余張力分布相近，這與文獻[8-9]中鋼制芯模下恒張力及恒力矩制度的剩余張力分布存在較大差異。錐度張力可減小藥柱芯模對張力的松弛所用，但前幾層的剩余張力仍為負數，纏繞時樹脂未固化，不能承載反向的壓縮應力。因此，負的剩余張力表示纏繞層已被完全放松，較大的應力狀態差異會導致纏繞層在固化過程中出現褶皺等質量問題，見圖3。

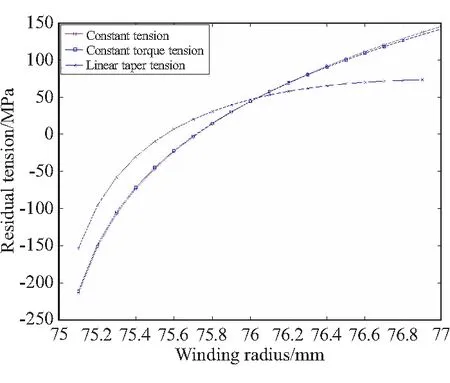
圖2 帶藥纏繞不同張力制度下纏繞層剩余張力曲線

圖3 恒張力制度下NOL環的褶皺缺陷

進一步分析等剩余張力制度，本文使用迭代搜索法[13]對等剩余張力制度進行求解，以纏繞16層為例，圖4給出了分別達到5、10、20、40 N等剩余張力狀態時需要施加的纏繞張力。可看到，使用等剩余張力制度時，纏繞張力在首層施加的最大，隨著纏繞層數的增加而遞減，且各層遞減的幅度逐漸降低。對于常規纏繞機，其施加張力的范圍在20～80 N之間，在該區間范圍內，已無法對帶藥柱纏繞復合殼體進行等剩余張力制度的纏繞。

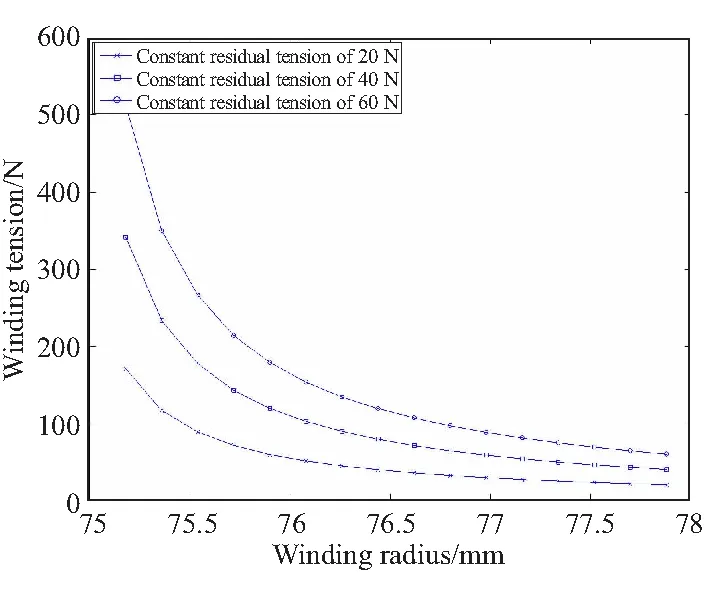
圖4 不同等剩余張力下的纏繞張力制度

3 基于粒子群算法的張力制度優化

以藥柱為纏繞芯模后，纏繞層剩余張力的變化明顯，工程中鋼芯模常用的遞減張力制度不再具有適用性，需要根據藥柱芯模的特點對張力制度進行優化。一個較為合理適用的方法就是以纏繞層剩余張力的梯度為目標進行優化，等剩余張力模型中，每一層的剩余張力為恒定值，剩余張力的梯度為零。因此，本文以纏繞層的剩余張力梯度之和最小式(5)為優化目標，對施加的纏繞張力進行優化。

(5)

粒子群優化算法(Particle swarm optimization algorithm，PSO)以其高精度、收斂快、算法簡單易于實現等優點，被廣泛地用于解決實際工程優化問題[22]。將PSO算法與纏繞過程相結合，每一組張力制度視為粒子群中的一個粒子，粒子的維度就是纏繞層數，如圖5所示。

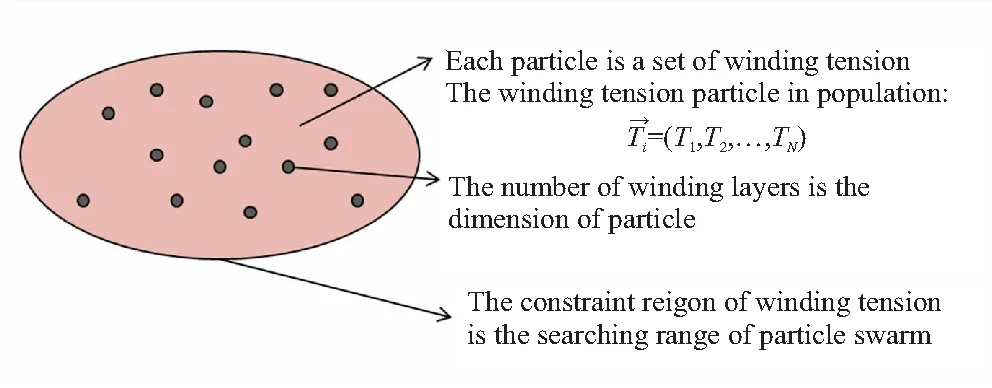
圖5 粒子群算法優化張力制度示意圖

使用式(6)確定個體和種群的最優位置。其中，Pis表示個體最優位置，Pgs表示全局最優位置。

(6)

使用式(7)更新粒子的速度和位置，c1和c2是學習因子，為非負常數，c1調節粒子向自身最好的方向前進，c2控制粒子向全局最優方向前進；r1和r2是相互獨立的偽隨機數，服從[0,1]上的均勻分布。

(7)

纏繞張力制度的PSO算法步驟如下：

(1)初始化規模為m的張力制度粒子群，對粒子群的位置和速度進行初始化；

(2)取式(5)為適應度計算公式，計算每個粒子的適應度值；

(3)使用式(6)確定個體最優位置Pis和種群最優位置Pgs；

(4)根據式(7)更新搜尋粒子的位置和速度；

(5)當迭代步數或適應度值達到設定值時，輸出纏繞張力制度。否則，返回第二步。

粒子群算法優化流程見圖6。

圖6 粒子群算法優化流程圖

根據文獻[19]中纏繞張力及強度關系的試驗結果，結合實際纏繞機可執行的張力范圍，帶藥柱纏繞的張力設定為20～60 N。在此范圍內，使用PSO對藥柱芯模NOL環環向纏繞的張力制度進行優化，具體過程為粒子群中每個粒子是一種張力制度，計算各張力制度下的剩余張力(即適應度值)，根據粒子群算法的位置和速度公式更新各粒子(張力制度)，在個體最優位置繼續尋找合適的張力制度，如此往復，直到滿足精度要求或達到預設的迭代次數。

圖7為PSO程序給出的適應度以及剩余張力的曲線，從迭代過程中適應度值變化曲線可看出，在迭代至200步后適應度趨于穩定，算法收斂，最終取整后得到的優化張力制度為

圖7 粒子群優化算法迭代過程及優化張力制度下的剩余張力分布

Tw=[60,40,31,25,21,20,20,20,20,20,20,20,20, 20,20,20]

可看到，首層張力達到給定上限60 N，逐層降低后達到給定下限20 N，這是由于藥柱芯模組件的模量較低，導致環向纏繞時的張力放松明顯，首層張力為最大預設值時，纏繞5層后其張力就已被完全放松，各層張力變化的梯度逐層減小，與理論分析中得出的結論相一致。

圖8給出了優化張力制度和常規張力制度下纏繞層剩余張力分布的對比。可看到，在優化張力制度下，纏繞層的剩余張力在前5層趨于一致，且各纏繞層剩余張力的梯度明顯降低，優化效果明顯。

4 試驗驗證

試驗依據國標GB/T 1458—2018“纖維纏繞增強塑料環形試樣力學性能試驗方法”中的規定進行，纖維使用東麗公司T700碳纖維，基體為自制的環氧體系低溫固化樹脂，纖維帶寬度3.5 mm，單層平均厚度0.18 mm。使用單環纏繞法在鋼芯模上纏繞了恒張力和逐層遞減2 N張力制度的NOL環，使用圓筒切環法在藥柱芯模上纏繞了恒張力和優化張力制度的NOL環，各類NOL環拉伸試樣7個，剪切試樣9個(從3個NOL環中均與切取)。鋼芯模及藥柱芯模NOL環見圖9。

(a)Steel mandrel NOL rings (b)Propellant mandrel NOL rings

圖10和圖11給出了不同張力制度下鋼芯模和藥柱芯模NOL環的拉伸和剪切性能，可得出：

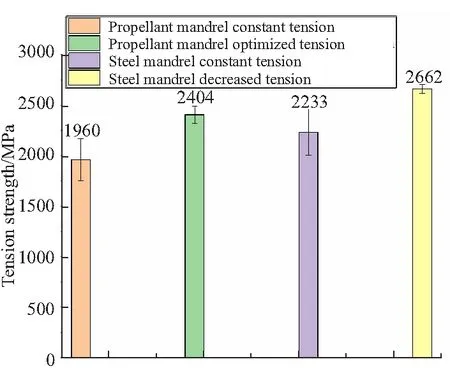
圖10 不同NOL環的拉伸強度

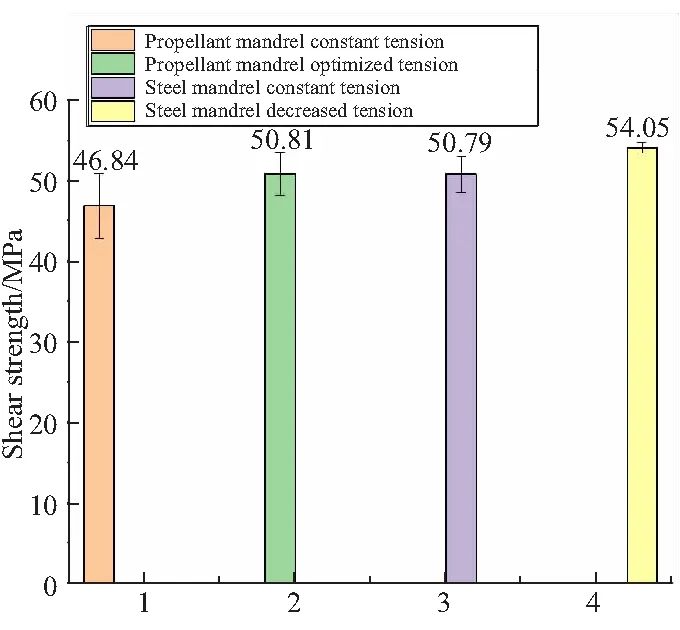
圖11 不同NOL環的剪切強度

(1)遞減2 N張力制度下鋼芯模NOL環力學性能最好，恒張力制度下藥柱芯模NOL環力學性能最差；

(2)在相同的纏繞芯模下，遞減2 N張力制度和優化張力制度下NOL環的力學性能較恒張力制度的要好，離散系數也較低，表明當纏繞層的剩余張力趨于一致后，NOL環的力學性能有所提升；

(3)使用藥柱芯模時，優化張力制度NOL環的拉伸強度和剪切強度較恒張力NOL環的分別提高了22.9%和8.4%，表明以“最小剩余張力梯度”為優化目標得到的優化張力制度，可提高NOL環的力學性能。

圖12(a)～(d)分別給出了鋼芯模NOL環和藥柱芯模NOL環的破壞模式。本文制備的NOL環除纏繞芯模和張力制度改變外，其余影響因素盡可能保持一致。因此，張力制度和纏繞芯模的差異是導致NOL環拉伸試件破壞模式不同的主要原因。優化張力制度NOL環纏繞層的剩余張力趨于一致，為整體拉斷形式的破壞，表明纖維同時承力，同時破壞，充分發揮了碳纖維的力學性能。

恒張力制度鋼芯模NOL環和藥柱芯模NOL環均存在局部分層斷裂的破壞模式，尤以藥柱芯模為甚，部分試件呈現出沿環向劈裂的破壞模式，見圖12(e)，其主原因為使用藥柱芯模后，各層剩余張力的梯度偏大，內層纖維的纏繞張力已被完全放松，固化成型后存在纖維層的褶皺或屈曲。拉伸時，存在缺陷的部位容易出現應力集中，導致纏繞層分層、劈裂，部分纖維提前拉斷，無法同時承載，影響了纖維強度的發揮。

(a)Steel mandrel with decrease 2 N per layer (b)Steel mandrel with constant winding tension

5 結論

本文對帶藥柱纏繞固體火箭發動機殼體成型中使用的張力制度進行了研究，對纏繞過程中藥柱芯模進行了分析，使用PSO算法對帶藥柱纏繞過程中的張力制度進行了優化，并對優化張力制度進行了試驗驗證，可指導高性能帶藥柱纏繞復合殼體的纏繞設計工作。

(1)使用藥柱推進劑作為芯模，其模量較低，張力松弛的原因主要是芯模發生徑向變形，從而造成纏繞層的張力放松，使用恒張力進行纏繞時，各層的剩余張力分布相差很大，易出現褶皺缺陷；

(2)使用優化張力制度纏繞的藥柱芯模NOL環，相比恒張力制度NOL環的拉伸強度提高了22.9%，剪切強度提高了8.4%，優化效果明顯。

以上結論表明，帶藥柱纏繞復合殼體成型過程中張力制度的選擇至關重要，纏繞結束后，各纏繞層趨向于等剩余張力狀態，可充分發揮纖維的力學性能，提高承載能力。

目前，關于纏繞層的剩余張力公式均基于彈性芯模推導而來，本文的分析模型及優化算法亦是使用彈性芯模假定，從優化結果來看，使用彈性芯模推導的優化張力制度具有一定效果，但實際中的推進劑藥柱為粘彈性材料，若想得到纏繞層準確的剩余張力，需要使用粘彈性材料的本構進行推導，這也是帶藥柱纏繞復合殼體張力制度設計的發展方向。