GM-Markov模型在船舶水上交通事故預測中的應用

李政良，杜柏松，劉然，高健

（浙江海洋大學 船舶與海運學院，浙江 舟山 316022）

0 引言

船舶水上交通安全長久以來一直受到國際社會的廣泛關注，船舶水上交通事故的預測是保障水上安全的一項重要內容。國際社會出現了一系列方法，如加權灰色理論預測法、BP神經網絡模型預測、博克斯-詹金斯法、時間序列預測法等用于船舶水上交通事故的預測。上述方法中，加權灰色理論預測[1]需要人為選取合適的權值矩陣，博克斯-詹金斯法[2-3]在預測長期的數據時預測精度趨于下降，BP神經網絡模型[4]往往導致局部極小化且程序復雜，另外還有時間序列等預測方法，在進行相關預測時均有不盡人意之處。灰色預測模型[5]實質上是利用時間響應函數即指數曲線去擬合實際值，但其對于振蕩幅度和速度較大的船舶水上交通事故數據的預測結果存在較大的偏差，而馬爾科夫預測是一個能夠反映隨機因素影響程度大小和修正偏離程度的動態系統。鑒于此，本文擬將馬爾科夫預測與灰色預測理論的優勢互補[6]，構造GM-Markov預測模型來對未來一段時間內的船舶水上交通事故數做出預測和判斷，經實例驗證計算表明該模型可以有效地減小預測序列的波動性，從而增加預測值的精確度，可以更為準確地進行船舶水上交通事故預測，為主管機關管控船舶的水上交通安全提供精確的數據支持。

1 GM-Markov預測模型

1.1 灰色GM（1.1）預測

根據選擇的數據設立原始序列為:X(0)（k）={x（1），x（2），…，x（n）}；設X（1）為X（0）的一階累加序列，則為：X（1）=(x(1)（1），x(1)（2），…，x(1)（n））；由累加序列構造一階線性方程：

1.2 馬爾科夫預測

馬爾科夫預測是對原始數據進行狀態劃分和估計轉移概率參數化并預測事物未來所屬狀態的隨機過程，其一般步驟如下。

1）劃分狀態區間。根據原始數據和灰色預測值的數值、數量和需要擬合的精度進行狀態區間的劃分。

2）計算轉移概率矩陣P。公式為

1.3 預測模型的精度檢驗

根據式（6）、式（7）可得出一個綜合評定預測模型的精度分級表，如表1所示。

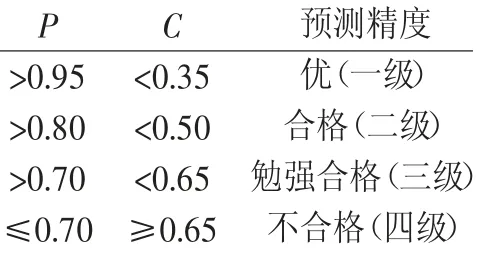
表1 預測精度等級劃分表

2 馬爾科夫模型在船舶水上交通事故中的應用

2.1 灰色GM（1,1）模型預測

根據我國交通運輸部每年發布的《交通運輸行業發展統計公報》，可查得2004—2018年我國船舶水上交通事故發生的事件數據如表2所示，由表2可以看出船舶水上交通事故的發生數量15年來總體呈下降趨勢，符合灰色預測模型的特點，故采用灰色GM（1,1）模型進行預測計算。

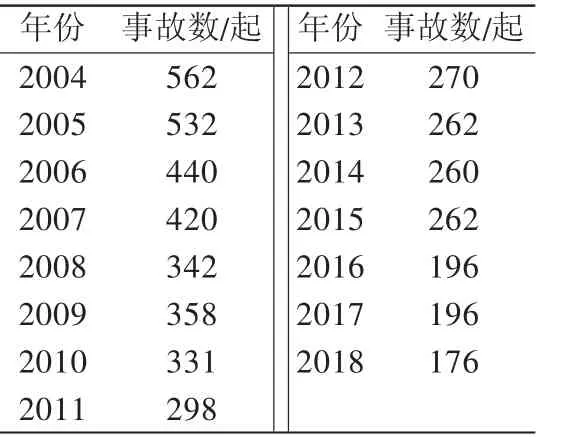
表2 2004—2018年我國船舶水上交通事故情況

按照灰色GM（1,1）模型構建過程進行以下程序：

選擇原始時間序列為

X（0）={X（1），X（2），…，X（15）}={562.0，532.0，440.0，420.0，342.0，358.0，331.0，298.0，270.0，262.0，260.0，262.0，196.0，196.0，176.0}。

將原始數列累加得累加生成數列為

X（1）={X（1）（1），X（1）（2），…，X（1）（15）}={562.0，1094.0，1534.0，1954.0，2296.0，2654.0，2985.0，3283.0，3553.0，3815.0，4075.0，4337.0，4533.0，4729.0，4905.0}。

計算X（1）的緊鄰生成值序列得

Y={y（1），y（2），…，y（15）}={1656.0，2628.0，3488.0，4250.0，4950.0，5639.0，6268.0，6836.0，7368.0，7890.0，8412.0，8870.0，9262.0，9634.0，4905.0}。

綜上計算可得船舶水上交通事故的灰色預測數值序列，如表3所示。

2.2 GM-Markov預測

根據灰色預測計算結果如表3所示，可知灰色預測的相對誤差平均值Q值達到了7.57%，預測模型的小概率誤差值P為0.933（0.80＜P＜0.950）, 預測模型的后驗差比值C為0.451（0.35＜C＜0.50）。由表1可知該模型的精度等級為二級，預測精度一般，只是達到了“合格”級別。通過表1可以看出，2004—2018年的船舶水上交通事故數據并非線性下降，而是有很大的波動性和復雜性；同時，由上文建模分析，馬爾科夫預測可以對灰色GM（1,1）預測值的振動幅度進行修正，因此將兩者結合起來進行船舶水上交通事故的預測計算，希望能提高預測精度。

根據船舶水上交通事故灰色預測值的相對誤差值，將預測情況分為4種狀態：低估（-0.0746，0.0005）、較準確（0.0005，0.0756）、高 估（0.0756，0.1507）、極 度 高 估（0.1507，0.2256），然后，通過確定2004—2018年我國船舶水上交通事故的分布狀態和年數，可得矩陣：

其中P(1)為一步轉移概率矩陣，則多步狀態轉移概率矩陣為P(n)=[P(1)]n。

據此可得出灰色預測的修正值，即灰色馬爾科夫預測模型的預測值，如表3所示。

3 船舶水上交通事故預測結果及分析

3.1 預測結果

通過灰色GM（1,1）模型和GM-Markov模型對船舶水上交通事故進行計算得到相應的預測值，如表3所示。

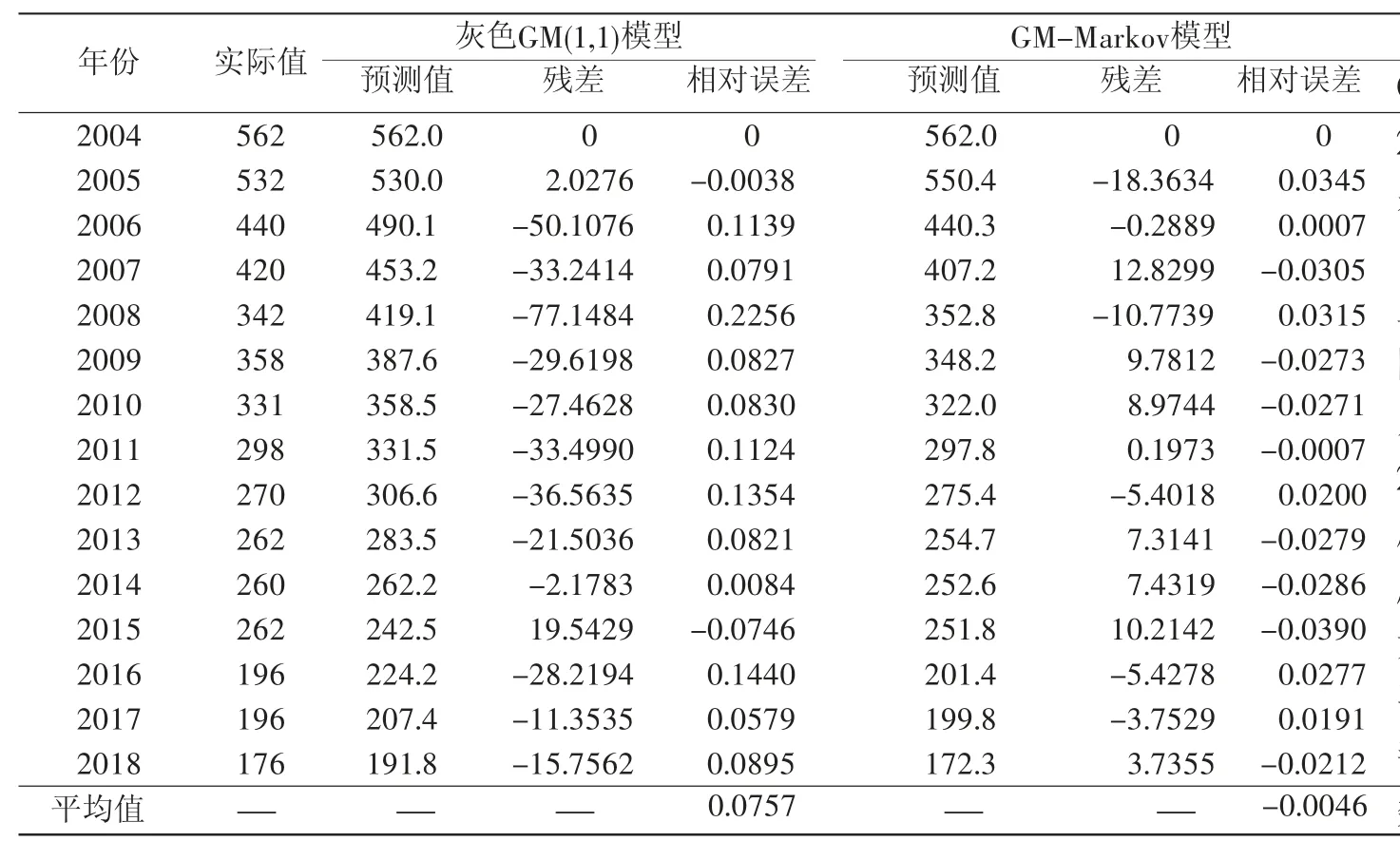
表3 灰色GM（1,1）模型與GM-Markov模型預測誤差對比

根據灰色預測和灰色馬爾科夫預測值結果，作2種預測模型預測值和實際值的對比曲線，如圖1所示。

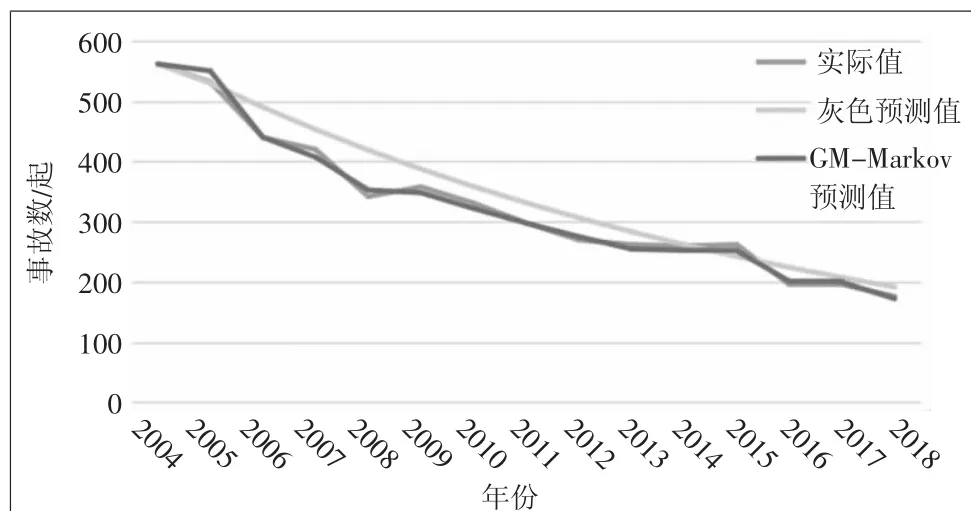
圖1 2種預測模型預測結果擬合曲線

3.2 GM-Markov模型的預測分析

3.2.1 GM-Markov模型預測精度分析

計算出2種預測模型的相對誤差均值、小概率誤差、后驗差比值，灰色預測模型的分別為7.6%、0.933、0.451，GM-Markov預測模型的分別為-0.46%、1.000、0.074，可以看出GM-Markov模型求得的預測值相對誤差平均值Q為-0.46%，明顯優于灰色預測預測值的Q值（7.57%），而且GM-Markov模型預測值曲線與實際值曲線走勢基本相同。根據誤差檢驗公式對我國船舶水上交通事故灰色預測值及GM-Markov模型預測值進行后驗差校驗，GMMarkov預測模型的小概率誤差值P為1（P＞0.950）, 預測模型的后驗差比值C為0.074（小于0.35），由表1預測精度等級劃分表知，GM-Markov模型的預測精度等級為一級（優），說明GM-Markov模型進一步提升了船舶水上交通事故預測中的精度。

3.2.2 GM-Markov模型的可行性分析

以2004—2018 年的船舶水上交通事故數作為原始數據對GM-Markov模型的可行性進行驗證，求出2004—2018年的預測值，通過預測值和實際值的比較可以發現，GM-Markov預測值與實際值非常接近，相對誤差僅為-0.46%，預測精度等級為一級（優）；完全符合對預測模型精度的要求，可以作為船舶水上交通運輸事故預測的優先選用模型。

利用船舶水上交通事故GM-Markov預測模型，對2019、2020、2021年進行預測，預測結果如表4所示。

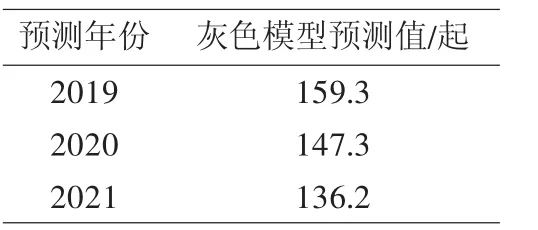
表4 2019-2021年水上交通事故GM-Markov預測值

由交通部發布的《2019年水上交通事故年報》可知2019年實際發生的船舶水上交通事故數為137起，預測值和真實值相差22.3起。究其原因，近年來我國政府加大了對運輸船舶的監管力度，船公司管理差、船況差、船員素質差等突出問題得到明顯解決，船舶水上交通環境持續改善，使得船舶水上安全交通事故數明顯降低。但是切不可掉以輕心，從歷史數據可以看出船舶水上交通事故數存在很大的隨機性和不規律性；同時，今年新冠疫情肆虐全球，給船員的換班和遣返造成很大影響，導致大量船員在船工作時間超過合同期，甚至超過STCW等國際公約規定的船員在船最長工作時間，船員疲勞、超期工作將給船舶安全帶來巨大隱患，希望相關部門能特別注意今年的船舶水上交通安全問題。

4 結語

1）通過對比分析灰色預測和GM-Markov模型預測各精度指標，發現GMMarkov模型相對于傳統的灰色預測模型而言，精度和擬合度更佳，能更好地描述船舶水上交通事故的未來走勢和數據序列的隨機波動變化。2）船舶水上交通事故數屬于具有固定趨勢但非線性變化的離散型數值，由本文預測研究可知，GM-Markov預測模型適合這樣的離散型數據的預測，可用于相關數據類型的預測計算，具有一定的普適性。3）根據近幾年統計數據變化可以看，出船舶水上交通事故數雖然呈下降趨勢，但數值跳躍性很大，考慮到受2020年新冠疫情影響，因船員換班困難導致大規模船員在船超期工作，這給船舶水上交通安全帶來了巨大隱患，相關部門應該對今年的水上交通安全形勢引起特別的重視。GM-Markov模型可以作為船舶水上交通事故預測的數據模型，GM-Markov模型相對更為精準的預測能幫助水上交通安全主管機關制定更為完善的預防措施，在誤差允許的范圍內，為船舶水上交通事故預測提供新的理論依據。