地鐵線路扣件剛度對(duì)鋼軌振動(dòng)與波磨的影響

朱寧 楊新文 趙治均

摘要：為探明整體道床軌道區(qū)段波磨發(fā)生機(jī)理及其對(duì)輪軌系統(tǒng)參數(shù)的影響規(guī)律，建立輪對(duì)和整體道床軌道三維有限元模型，分析輪軌共振模態(tài)與整體道床鋼軌振動(dòng)特性，探討鋼軌扣件剛度和輪對(duì)振動(dòng)模態(tài)對(duì)整體道床區(qū)段鋼軌波磨的影響規(guī)律。結(jié)果表明：鋼軌扣件剛度主要影響鋼軌起跳共振頻率，而對(duì)鋼軌pinned-pinned共振頻率影響甚微;較低的扣件剛度將激發(fā)鋼軌較大的振動(dòng)，在特定頻段上過大的鋼軌振動(dòng)會(huì)導(dǎo)致對(duì)應(yīng)波長波磨的加劇，進(jìn)而加速波磨的發(fā)展;鋼軌在358?Hz下的橫向彎曲變形是地鐵整體道床區(qū)段線路產(chǎn)生特征波長為40?mm波磨的主要原因，故可采取減振措施抑制輪軌系統(tǒng)在358?Hz處的橫向振動(dòng)響應(yīng)，從而抑制波磨的產(chǎn)生和發(fā)展。

關(guān)鍵詞：地鐵;整體道床;無砟軌道;扣件;車輪;振動(dòng);鋼軌波磨;有限元

中圖分類號(hào)：TP391.99;U213.53

文獻(xiàn)標(biāo)志碼：B

文章編號(hào)：1006-0871（2021）03-0049-06

DOI：10.13340/j.cae.2021.03.009

Abstract：To?explore?the?mechanism?of?rail?corrugation?in?monolithic?ballast?bed?track?section?and?its?influence?on?wheel?rail?system?parameters，?the?three-dimensional?finite?element?model?of?wheel?set?and?monolithic?ballast?bed?track?is?established.?The?wheel?rail?resonance?mode?and?the?vibration?characteristics?of?monolithic?ballast?bed?rail?are?analyzed，?and?then?the?effects?of?rail?fastening?stiffness?and?wheel?set?vibration?mode?on?rail?corrugation?in?monolithic?ballast?bed?section?are?studied.?The?results?show?that?the?rail?fastening?stiffness?mainly?affects?the?rail?take-off?resonance?frequency，?but?affects?little?on?the?pinned-pinned?resonance?frequency.?The?lower?rail?fastening?stiffness?stimulates?the?greater?vibration?of?the?rail，?and?the?excessive?rail?vibration?in?a?specific?frequency?band?aggravates?the?rail?corrugation?of?the?corresponding?wavelength，?so?as?to?accelerate?the?corrugation?development.?The?transverse?bending?deformation?of?rail?at?358?Hz?is?the?main?reason?for?the?characteristic?wavelength?of?40?mm?rail?corrugation?in?the?monolithic?ballast?bed?section?of?metro.?Therefore，?vibration?reduction?measures?can?be?taken?to?suppress?the?lateral?vibration?response?of?wheel?rail?system?at?358?Hz，?and?then?the?generation?and?development?of?rail?corrugation?can?be?restrained.

Key?words：metro;monolithic?ballast?bed;ballastless?track;rail?fastening;wheel;vibration;rail?corrugation;finite?element

0?引?言

鋼軌波磨是長期困擾鐵路建設(shè)的問題，尤其是在重載鐵路建設(shè)中，這一問題更嚴(yán)重。我國城市軌道交通發(fā)展迅猛，尤其是軌道投入運(yùn)行超過30年后，鋼軌波磨問題越來越成為困擾城市軌道交通工務(wù)維修養(yǎng)護(hù)人員的一個(gè)重要問題[1]。鋼軌波磨不會(huì)實(shí)質(zhì)性地影響鋼軌的使用和行車安全，但在波磨嚴(yán)重的地段，列車振動(dòng)和噪聲增大，輪軌受力增大，扣件系統(tǒng)和車輛轉(zhuǎn)向架容易產(chǎn)生裂紋[2]，進(jìn)而出現(xiàn)軌道部件破損（見圖1），使軌道交通的運(yùn)營成本增加，并影響軌道交通的運(yùn)行安全。

各國學(xué)者對(duì)鋼軌波磨的發(fā)生機(jī)理、特征和控制措施進(jìn)行諸多研究，鋼軌波磨的發(fā)生機(jī)理是認(rèn)識(shí)并控制波磨的前提。目前，學(xué)者們最為認(rèn)可的波磨機(jī)理是固定波長機(jī)理和損傷機(jī)理。GRASSIE[3]將波磨按照不同的固定波長機(jī)理和損傷機(jī)理分為響軌波磨、車轍型波磨、P2力共振波磨、重載波磨、輕軌波磨和軌道形式波磨等6類。谷永磊[4]研究分析高速鐵路無砟軌道鋼軌波磨的成因與分類。金學(xué)松等[5]按照波磨是與系統(tǒng)固有特性相關(guān)還是由初始不平順發(fā)展而來，將其成因總結(jié)為自激振動(dòng)理論、反饋振動(dòng)理論和其他理論等3類。鋼軌波磨發(fā)生機(jī)理復(fù)雜，影響因素眾多，與車輛-軌道結(jié)構(gòu)系統(tǒng)中各個(gè)部分均有一定關(guān)聯(lián)，因此至今未有一種統(tǒng)一的機(jī)理解釋各種波磨現(xiàn)象。在對(duì)實(shí)際線路中發(fā)生波磨的機(jī)理進(jìn)行研究時(shí)，需要綜合車輛、線路、軌道、輪軌關(guān)系等各方面，研究梳理出誘發(fā)鋼軌引起波磨的關(guān)鍵影響因素。

為控制地鐵線路環(huán)境振動(dòng)，各種類型的減振軌道涌現(xiàn)。研究表明，在各種類型的減振軌道上，鋼軌波磨發(fā)生的概率仍均較大[6-7]。鋼軌高彈性扣件是一種有效的軌道減振結(jié)構(gòu)，可以較好地控制列車引起的環(huán)境振動(dòng)，但減振扣件軌道區(qū)段的鋼軌波磨問題愈發(fā)凸顯，如先鋒扣件、浮軌等[8]。已有研究大多數(shù)集中在現(xiàn)場觀測的定性詮釋上[9]，對(duì)于整體道床減振扣件地段鋼軌波磨的理論仿真、軌道結(jié)構(gòu)參數(shù)與輪軌關(guān)系的匹配方面研究較少。鐘碩喬等[10]將實(shí)測鋼軌短波波磨不平順數(shù)據(jù)作為不平順激勵(lì)，通過數(shù)值計(jì)算，得到在科隆蛋扣件線路上不平順發(fā)展過程中車輛動(dòng)力學(xué)響應(yīng)的變化情況。

為探明整體道床軌道區(qū)段波磨發(fā)生機(jī)理及其對(duì)輪軌系統(tǒng)參數(shù)的影響規(guī)律，以蘇州城市軌道交通為研究對(duì)象，建立輪對(duì)和整體道床軌道三維有限元模型，分析輪軌共振模態(tài)與整體道床軌道鋼軌導(dǎo)納特性，研究該區(qū)段鋼軌波磨的產(chǎn)生原因，探討鋼軌扣件剛度與輪對(duì)振動(dòng)模態(tài)對(duì)整體道床軌道區(qū)段鋼軌波磨的影響規(guī)律。

1?軌道和輪對(duì)有限元模型

1.1?整體道床軌道有限元模型

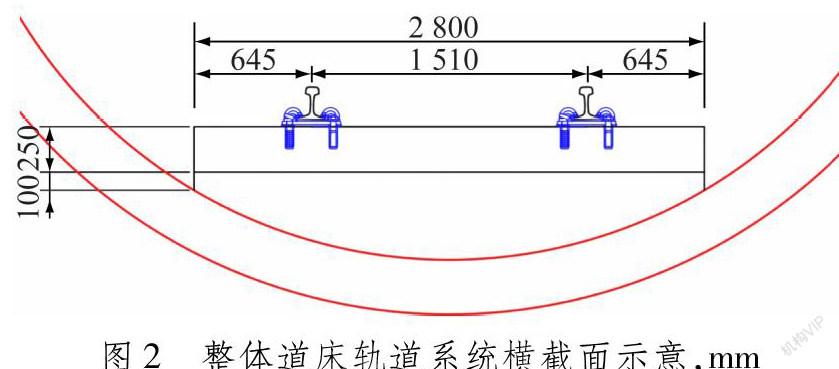
為系統(tǒng)研究分析蘇州城市軌道交通整體道床區(qū)段的鋼軌振動(dòng)特性，采用有限元軟件Abaqus建立整體道床軌道結(jié)構(gòu)三維實(shí)體有限元模型。軌道結(jié)構(gòu)有限元模型的參數(shù)參考蘇州城市軌道交通實(shí)際建設(shè)線路的設(shè)計(jì)參數(shù)，其橫截面參數(shù)見圖2，有限元模型的動(dòng)力學(xué)參數(shù)見表1。

針對(duì)所建立的軌道系統(tǒng)三維實(shí)體有限元模型，使用Lanczos法進(jìn)行軌道系統(tǒng)模態(tài)分析，提取軌道系統(tǒng)的固有頻率及其對(duì)應(yīng)模態(tài)，分析軌道系統(tǒng)容易產(chǎn)生激烈動(dòng)力響應(yīng)的激勵(lì)頻率及其對(duì)應(yīng)的振動(dòng)形態(tài)。在鋼軌和軌下結(jié)構(gòu)模型中，為降低內(nèi)部動(dòng)力波的端部反射對(duì)軌道結(jié)構(gòu)振動(dòng)特性的影響，鋼軌縱向長度應(yīng)足夠長。參考國內(nèi)外有關(guān)的計(jì)算模型[11]，確定軌道系統(tǒng)的模型長度為25?m，可以反映列車運(yùn)行過程中近似無限長鋼軌的振動(dòng)特性。軌道系統(tǒng)結(jié)構(gòu)在橫截面上均為對(duì)稱結(jié)構(gòu)，為提高計(jì)算速度，建立單股軌道結(jié)構(gòu)的對(duì)稱模型。最終建立的整體道床軌道三維有限元模型見圖3。

1.2?輪對(duì)有限元模型

車輛輪對(duì)同樣參考蘇州城市軌道交通運(yùn)營廣泛使用的B型電客車的有關(guān)設(shè)計(jì)數(shù)據(jù)，其中車輪的主要參數(shù)為軸重14?t、輪徑840?mm，軸型為RC3。建立的車輛輪對(duì)三維有限元模型見圖4。

2?整體道床軌道導(dǎo)納特性與波磨關(guān)系

2.1?輪對(duì)與整體道床軌道模態(tài)分析

2.1.1?整體道床軌道模態(tài)分析

整體道床無砟軌道在0～2?000?Hz范圍內(nèi)共有2?332階模態(tài)，其前50階固有頻率見表2，軌道的典型振型見圖5。由此可知，整體道床無砟軌道的軌下基礎(chǔ)幾乎不參與振動(dòng)，前12階振型為鋼軌的橫向彎曲變形，從第13階開始以鋼軌的垂向彎曲變形為主，其中第16階振型伴有鋼軌的橫向彎曲。

2.1.2?輪對(duì)模態(tài)分析

對(duì)城市軌道交通B型車的輪對(duì)進(jìn)行自由模態(tài)分析，即不加任何外部約束，使其具有與動(dòng)力學(xué)模型相同的自由度。與軌道系統(tǒng)模態(tài)分析方法相同，最終得到輪對(duì)在0～2?000?Hz范圍內(nèi)的固有頻率及其對(duì)應(yīng)的振型。輪對(duì)的固有頻率及其典型振動(dòng)分布分別見圖6和7。

輪對(duì)的振動(dòng)形式有徑向振動(dòng)、軸向振動(dòng)、徑向彎曲和軸向彎曲等。

2.2?整體道床軌道導(dǎo)納特性分析

為全面反映鋼軌的振動(dòng)特性，計(jì)算0～10?000?Hz頻率范圍內(nèi)的垂向和橫向鋼軌位移導(dǎo)納，計(jì)算步長為1?Hz。對(duì)于整體式道床軌道系統(tǒng)，鋼軌垂向位移導(dǎo)納見圖8。鋼軌在不同頻率下均會(huì)產(chǎn)生振動(dòng)，其中有2種典型的振動(dòng)形式，對(duì)應(yīng)各個(gè)導(dǎo)納峰值：鋼軌共振和pinned-pinned共振。鋼軌共振頻率即導(dǎo)納圖中的第一個(gè)峰值對(duì)應(yīng)頻率180?Hz。鋼軌pinned-pinned振動(dòng)是指支撐于兩根軌枕之間的鋼軌受到激勵(lì)后產(chǎn)生的縱向機(jī)械波，其駐波節(jié)點(diǎn)剛好在軌枕處。第一個(gè)峰值之后的各個(gè)峰值均屬于pinned-pinned振動(dòng)，其頻率主要有1?100、3?160、5?138和7?800?Hz。

整體式道床軌道系統(tǒng)的鋼軌橫向位移導(dǎo)納見圖9。其振動(dòng)特性與重型鋼彈簧軌道結(jié)構(gòu)的鋼軌類似，有2種典型的振動(dòng)形式：橫向鋼軌共振和橫向pinned-pinned共振，并且在190～508?Hz頻率范圍內(nèi)持續(xù)震蕩，存在一系列導(dǎo)納峰值，此頻段的振動(dòng)與線路的短波長波磨關(guān)系密切。

綜合分析圖8和9可知，在列車運(yùn)行過程中，整體式道床軌道系統(tǒng)的鋼軌振動(dòng)響應(yīng)峰值頻率主要有104、180、190、212、238、263、294、326、360、405、434、471、508、684、842和1?100?Hz等，在這些頻率下，鋼軌的動(dòng)力響應(yīng)更加劇烈，可能由此產(chǎn)生更加嚴(yán)重的鋼軌磨耗。結(jié)合軌道系統(tǒng)和輪對(duì)模態(tài)分析結(jié)果，在列車運(yùn)行過程中容易發(fā)生劇烈的輪軌共振而造成嚴(yán)重磨耗的頻率主要有263、358、405和471?Hz，對(duì)應(yīng)頻率下的輪軌振動(dòng)模態(tài)見圖10。

進(jìn)一步結(jié)合蘇州城市軌道交通的波磨現(xiàn)場實(shí)測數(shù)據(jù)，在線路區(qū)段處，其現(xiàn)場工程情況條件與所建立的整體道床軌道三維實(shí)體有限元模型相同，經(jīng)過現(xiàn)場測試數(shù)據(jù)處理和分析[12]，得到其波磨特征波長為40和200?mm。此區(qū)段列車的實(shí)際運(yùn)營車速為50?km/h，短波波磨的特征波長40?mm對(duì)應(yīng)頻率約為347?Hz。考慮到實(shí)際運(yùn)營過程中的車輪輪對(duì)的附加質(zhì)量，相同振動(dòng)形態(tài)下輪軌系統(tǒng)的動(dòng)力響應(yīng)頻率應(yīng)略低于軌道系統(tǒng)本身在外界單獨(dú)激勵(lì)下的振動(dòng)頻率，因此該線路的短波波磨對(duì)應(yīng)的鋼軌振動(dòng)頻率應(yīng)約為358?Hz。由圖10b可知，此頻率下鋼軌和輪對(duì)的振動(dòng)形態(tài)以橫向振動(dòng)為主，也就是說，鋼軌在358?Hz下的橫向彎曲變形是此區(qū)段線路產(chǎn)生特征波長為40?mm波磨的主要原因。通過采取減振措施，重點(diǎn)抑制輪軌系統(tǒng)在358?Hz處的橫向振動(dòng)響應(yīng)，降低鋼軌在此頻率的振幅，可以降低對(duì)應(yīng)波長的周期性鋼軌磨耗，進(jìn)而抑制波磨的產(chǎn)生和發(fā)展。

2.3?扣件剛度的影響分析

2.3.1?扣件垂向剛度

在保持其他參數(shù)不變的情況下，分別將扣件垂向剛度取值5、10、20、30、40和50?kN/mm，計(jì)算分析鋼軌跨中簡諧力激勵(lì)下激勵(lì)點(diǎn)處鋼軌的垂向?qū)Ъ{，結(jié)果見圖11。

改變軌道系統(tǒng)的扣件垂向剛度，主要影響鋼軌在0～1?000?Hz頻率范圍內(nèi)的垂向振動(dòng)特性。具體來說，鋼軌在10和200?Hz附近的導(dǎo)納峰值明顯改變，但不會(huì)影響鋼軌的pinned-pinned振動(dòng)。當(dāng)扣件垂向剛度過小（小于5?kN/mm）時(shí)，該峰值頻率接近20?Hz從而表現(xiàn)不明顯，整個(gè)頻段內(nèi)鋼軌的振幅都很大。在特定頻段上，過大的鋼軌振動(dòng)會(huì)導(dǎo)致對(duì)應(yīng)波長的磨耗加劇，從而加速波磨的發(fā)展。在與波磨特征波長相關(guān)的364?Hz附近，存在一系列導(dǎo)納峰值，適當(dāng)增大扣件剛度可以明顯降低振幅，有助于抑制波磨的發(fā)展。

2.3.2?扣件橫向剛度

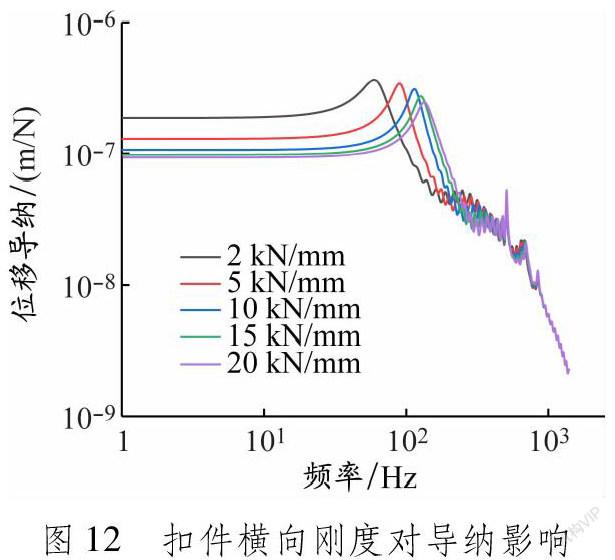
在保持其他參數(shù)不變的情況下，分別取鋼軌扣件橫向剛度值為2、5、10、15和20?kN/mm等5種情況，計(jì)算分析鋼軌跨中簡諧力激勵(lì)下激勵(lì)點(diǎn)處鋼軌的橫向?qū)Ъ{，見圖12。

改變鋼軌扣件橫向剛度，主要影響鋼軌0～800?Hz頻率范圍內(nèi)的橫向振動(dòng)特性。具體來說，鋼軌在100?Hz附近、160～500?Hz中多個(gè)頻率和700?Hz附近的導(dǎo)納峰值明顯改變，但不影響800?Hz附近的振動(dòng)峰值，說明增大扣件橫向剛度會(huì)導(dǎo)致該峰值頻率提高，對(duì)應(yīng)的導(dǎo)納峰值同時(shí)略微減小。在與波磨特征波長相關(guān)的頻率364?Hz附近，存在一系列導(dǎo)納峰值，適當(dāng)增大扣件橫向剛度可以明顯降低振幅，有助于抑制波磨的發(fā)展。

3?結(jié)?論

建立輪對(duì)和整體道床軌道三維有限元模型，進(jìn)行模態(tài)分析和導(dǎo)納分析，研究線路扣件剛度對(duì)鋼軌導(dǎo)納特性與波磨的影響，得到以下結(jié)論。

（1）?鋼軌扣件剛度主要影響鋼軌起跳共振頻率，對(duì)鋼軌pinned-pinned共振頻率影響甚微。

（2）?鋼軌扣件剛度降低，將激發(fā)鋼軌較大的振動(dòng)，在特定頻段上過大的鋼軌振動(dòng)會(huì)導(dǎo)致對(duì)應(yīng)波長波磨的加劇，進(jìn)而加速波磨的發(fā)展。在與波磨特征波長相關(guān)的400?Hz附近，存在一系列導(dǎo)納峰值，適當(dāng)增大扣件剛度可以明顯降低振幅，有助于抑制波磨的發(fā)展。

（3）?鋼軌在358?Hz下的橫向彎曲變形是此區(qū)段線路產(chǎn)生特征波長為40?mm波磨的主要原因，可通過采取減振措施，重點(diǎn)抑制輪軌系統(tǒng)在358?Hz處的橫向振動(dòng)響應(yīng)，降低鋼軌在此頻率的振幅，降低對(duì)應(yīng)波長的周期性鋼軌磨耗，進(jìn)而抑制波磨的產(chǎn)生和發(fā)展。

參考文獻(xiàn)：

[1]?ZHAO?X，?WEN?Z?F，?WANG?H?Y，?et?al.?Modeling?of?high-speed?wheel-rail?rolling?contact?on?a?corrugated?rail?and?corrugation?development[J].?Journal?of?Zhejiang?University：Science?A，?2014，?15（12）：946-963.

[2]?李偉.?地鐵鋼軌波磨成因及其對(duì)車輛/軌道行為的影響[D].?成都：西南交通大學(xué)，?2015.

[3]?GRASSIE?S?L.?Rail?corrugation：Characteristics，?causes，?and?treatments[J].?Proceedings?of?Institution?of?Mechanical?Engineers，?Part?F：Journal?of?rail?and?rapid?transit，?2009，?223（6）：581-596.?DOI：10.1243/09544097JRRT264.

[4]?谷永磊.?高速鐵路無砟軌道鋼軌波浪形磨損機(jī)理研究[D].?北京：北京交通大學(xué)，?2017.

[5]?金學(xué)松，?李霞，?李偉，?等.?鐵路鋼軌波浪形磨損研究進(jìn)展[J].?西南交通大學(xué)學(xué)報(bào)，?2016，?51（2）：264-273.?DOI：10.3969/j.issn.0258-2724.2016.02.006.

[6]?關(guān)慶華，?張斌，?熊嘉陽，?等.?地鐵鋼軌波磨的基本特征、形成機(jī)理和治理措施綜述[J].?交通運(yùn)輸工程學(xué)報(bào)，?2021，?21（1）：316-337.?DOI：10.19818/j.cnki.1671-1637.2021.01.015.

[7]?李響.?地鐵減振軌道結(jié)構(gòu)振動(dòng)及鋼軌波磨研究[D].?北京：北京交通大學(xué)，?2019.

[8]?CUI?X?L，?CHEN?G?X，?YANG?H?G，?et?al.?Study?on?rail?corrugation?of?a?metro?tangential?track?with?Cologne-egg?type?fasteners[J].?Vehicle?System?Dynamics，?2016，?54（3）：353-369.?DOI：10.1080/00423114.2015.1137955.

[9]?張厚貴.?北京地鐵鋼軌波磨的機(jī)理及整治方案研究[D].?北京：北京交通大學(xué)，?2015.

[10]?鐘碩喬，?吳磊，?李偉，?等.?鋼軌波磨對(duì)地鐵車輛動(dòng)力學(xué)響應(yīng)的影響[J].?計(jì)算機(jī)輔助工程，?2012，?21（6）：26-30.?DOI：10.3969/j.issn.1006-0871.2012.06.006.

[12]?楊新文，?翟婉明.?軌道交通輪軌噪聲機(jī)理、預(yù)測與控制[M].?上海：同濟(jì)大學(xué)出版社，?2017：40-46.

（編輯?武曉英）