基于數學建模思想的初中數學應用題的教學策略研究

葉麗平 梁衛超

摘 要：本文以初中階段數學課程中的應用題教學策略為研究對象，嘗試引入數學建模思想，對具體教學方案形成指導，以此完成初中數學應用題教學模式的方法升級，為一線教育工作提供實踐指導方案.

關鍵詞：初中數學;建模思想;應用題;教學策略

中圖分類號：G632 ? ? ?文獻標識碼：A ? ? ?文章編號：1008-0333（2021）32-0054-02

收稿日期：2021-08-15

作者簡介：葉麗平（1976.7-），女，江蘇省連云港人，本科，中學一級教師，從事初中數學教學研究.

梁衛超（1974.11-），男，江蘇省宿遷人，本科，中學一級教師，從事初中數學教學研究.

初中階段的數學課程尤為重要，是學生形成學科思維模式的關鍵時期.在實際教學工作中，對于應用型人才的需求，以及教育工作的升級發展，要求對數學學科教學內容進行創新調整，發揮數學建模思想優勢，幫助學生更加系統、深刻地認識學科知識體系，通過應用題解答，提高數學學科能力.而對這一應用內容的分析，應從數學建模思想的適應性入手，結合實踐策略展開探討.

一、數學建模思想在初中數學教學中的適應性

數學建模思想，是對實際事務的數學化處理，將實際事務中的抽象內容，提取出來，以更具邏輯性的特征完成表達.在初中數學課程中的應用，數學建模思想本身就帶有明顯的學科適應性.尤其在處理應用題類型的數學問題時，能夠在數學學科知識與實際情況間，建立起邏輯性的聯系，在幫助學生了解數學思維、掌握數學思維、應用數學思維分析實際問題上，有著明顯的指導作用.

尤其數學模型思想中的實踐模型搭建，不僅可以將學生的思維轉化為實踐操作，也能在具體的動手中，提高學生的綜合能力.宏觀上，這一內容也深入地迎合了素質教育的理念，是現代化教育發展的重要途徑.

二、數學建模思想在初中數學應用題教學中的應用策略 ?1.深度開發教材，提高學生數學能力

當前，初中教育應用的數學課程教材，是教育部統一編撰的專業教學材料.在系統性、科學性、教育性、指導性等條件上，有明顯的優勢效果.在數學應用題的建模思想教學應用中，深度開發課程教材，不僅可以提高教學質量，也能有效地提高學生的數學能力.從教育的宏觀視角來看，這種對統一教材的開發，也可以保證數學建模思想的應用推廣，實現教育整體升級的應用目標.以初一教材為例，在鴿子與鴿籠問題中，應從數學建模思想的角度入手，引導學生進行解題分析.首先，教師應讓學生對應用題題目進行分析，確定其中的關鍵詞句，然后以此類詞句為基礎，建立起等量關系模型.課堂上，學生就未知數問題，常出現意見分歧，存在兩種不同意見.一類是將鴿子的數量作為未知數，而另一種則傾向于將鴿籠的數量作為未知數.對此，可以對兩種意見進行統一，形成一種等量關系.由此，不僅統一了學生的意見，也將數學模型的基本思想引入課堂.接下來，教師可以使用代數式，進行數學語言轉化，將數學應用題，以數字等量關系的形式呈現出來，并通過方程未知量的求解，完成數學模型的等量關系分析.

2.鞏固課程知識，聯系生活實際問題

初中階段，應當加強學生對基礎知識的掌握，并在實際應用中進行鍛煉，以此提高學生處理實際問題的綜合能力.初中數學的應用題型，就是本著這一初衷設置的.在引入數學模型思想過程中，也要強調與實際問題的關聯性，以此保證題型類別特征的充分發揮.例如，在七年級上冊教材第三章《一元一次方程》的教學過程中，教師可以結合課程知識，聯系生活實際問題，對課程知識進行轉化，將數學語言轉換到具體的生活問題中.案例引導中，可以設置兩個牧童，其中，甲對乙說：“把你的羊給我一只，我的羊數量就是你的2倍”.乙回答“如果你給我一只，咱們倆羊的數量就相同了”.在這一例題中，教師可以幫助學生設置“審題、設元、建模、解答”的解題思路.審題中，根據甲和乙對話，確定兩個羊群的數量關系.然后在設元分析中，確定未知量，設甲的羊群中羊的只數為“X”，得出乙羊群中羊的只數為“（X-2）”.再根據對話內容，確定該應用題的等量條件，并列出方程式“（X+1）=2（X-2-1）”.最后，進入建模階段，通過這一例題，引導學生對這一問題進行分析，確定這一數學語言應用的特征，并從中總結出一般規律.由此，引導出此類應用題的轉化與求解方式，并與大量實際應用問題銜接，讓學生熟悉并掌握此類型題目的計算方式.又如，在對《生活中的反比例關系》這一課程教學中，教師可以將“踩氣球”這一游戲項目作為案例，引導出波義爾定律.在向學生提出pV=k（k為常數，k>0）這一公式之后，提出氣球內氣體壓強p是它體積的反比例函數，并以此假設為基礎，寫出解析式p=k/V（k為常數，k>0）.通過這一分析，確定數學建模分析的多種應用條件，以實現教材內容的深度開發與教學引導應用.

3.使用邏輯導圖，引導學生形成思維體系

邏輯導圖在教學中有著天然的適應性，可以清晰地反應知識脈絡，并幫助學生構建學科思維體系.例如，教師在課程講解中，可以使用多媒體課程軟件，對課程內容進行梳理，并將抽象圖形整理成思維導圖，加深學生對于數學模型思考方式的理解.方法上，可以用課件模擬小蟲向上爬行的軌跡，現將一棵樹干做好數字距離標記.然后以動圖的方式，設置一只瓢蟲向上爬行.先向上爬行30cm，然后，再向下爬行到原點，并繼續前進15cm.此時，完成展示之后，教師可使用數學邏輯導圖的方式，完成對于課題內容的分析，并讓學生更加清晰地完成數學概念模型的量級關系.通過這一量化關系，再整理出數學應用題目的課程邏輯體系，引導學生進行邏輯分析，以此積累量化課程知識.在應用數學模型思維開展教學的過程中，這一教學輔助工具，也可以發揮出其優勢作用，通過對思考方式的整理，幫助學生快速進入狀態，完成課程知識內容的學習，保證綜合能力的成長.

4.結合社會熱點，滲透完成建模分析

數學學科與實際生活有著天然的聯系，數學應用題是處理實際生活問題的類型化計算模型.在教學工作中，應主動追蹤社會熱點問題，在吸引學生注意力的同時，保證學生對于課程學習內容的興趣.另外，對于課程熱點內容的追蹤，也能在一定程度上，提高學生的成就感，并對課程知識的內容作出主動的延展分析，進而更好的將數學建模思想與建模分析方法滲透給學生.例如，教師可以結合春、秋學期天氣變化的特征，在囑咐學生注意保暖的同時，結合教材八年級下冊中，第二十章《數據的分析》中的課后習題，引導出“體制健康測試中的數據分析”這一課題.在分析中，將天氣變化中的實際氣候條件作為引導，在關心學生體制健康狀態的過程中，引入了數學知識.由此，將學生的注意力自然地引導到了數學學科知識中，采用數學建模的分析方式，統計健康測試中的具體數據資料，在滲透建模分析條件與方法的同時，也保證了學生的成長狀態.

5.設置開放主題，激發學生自主能力

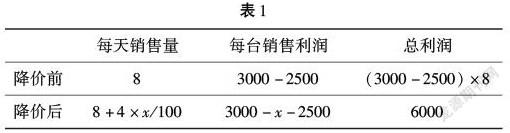
當前的素質教育環境中，應注重學生對于課程知識的主觀能動性.數學應用題課程教學，可以借助數學建模思想，創建開放性的課程主題，利用學生發散性的思維模式與積極的態度，自主地完成課程知識內容的學習.對此，教師可嘗試項目教學策略，在學生掌握一定數學建模思想后，通過小組式的開放性課題項目，保證學生對于課程知識的參與度，自主設計課程知識的學習計劃，完成應用題類型知識的解答.講解《一元二次方程》中，可將學生劃分為多個學習小組，以教學案例為引導，自主性地完成數學模型設置，在小組合作的過程中，將類項目的形式，保證整體分析的執行效果.例如，有的學生利用課余時間，對新華商場的某一冰箱產品進行市場調查，在確定冰箱進貨價為2500元的條件下，展開市場調查.當冰箱的銷售價格調整到3000元之后，一個星期平均每個工作日的銷售量可以達到8臺.而當銷售價格下調100元后，平均每個工作日可以多銷售冰箱4臺.在與實際需要相對接的條件下，如果這一商場的冰箱銷售專柜，每天想達到6000元的利潤水平，需要將每臺冰箱的銷售價格調整至多少.在學生充分調查分析后，就可根據建模分析的方式，對這一具體應用條件進行數學語言轉化.確定項目設置的問題之后，可以與另一課題小組進行對換，讓其他小組對這一問題進行解答分析.通過模型化處理，總結出“數量×單價=總價”、“數量×每件的利潤=總利潤”這兩個建立模型的基本關系.同時，根據數據變化模型，制作出這一項目的數量關系表格（如下表1所示）并完成模型求解.

綜上，通過對教材開發、課程鞏固、思維建設、熱點引入、開放主題這四個方面的建設，可以將數學學科中的建模思想，有效地對接到初中數學課程的應用題教學中.以此，不僅加深了學科思想對于學生的教育影響，也實現了初中數學課程的教學應用升級，是新時代素質教育人才需求下的教學方式轉變，可為課程改革升級，提供開放性的發展思路與應用空間.

參考文獻：

[1]李培新.小學數學應用題教學中激發學生學習興趣的有效方法探討[J].課程教育研究，2019（40）：167-168.

[2]蔡映霞.情境應用題的構造及其在初中小組合作學習教學中的應用[J].數學學習與研究，2019（08）：145-146.

[3]賈懷明.關于初中數學教學中培養學生邏輯思維能力的策略探討[J].課程教育研究，2018（49）：128.

[責任編輯：李 璟]