基于對比機制和算法因子的蜂群優化算法*

陳政 張明

（江蘇科技大學計算機學院 鎮江 212000）

1 引言

人工蜂群算法［1］（Artificial Bee Colony）是一種屬于啟發類型的群智能算法，Karaboga在2005年首次提出［2］，其是模仿蜜蜂采蜜機制，用于最優解的搜索，人工蜂群算法在求解過程中，可以不需要與問題相關的梯度信息，算法具有控制參數少，易于實現等優勢，受到越來越多的關注，已被應用于數據挖掘、圖像處理、神經網絡等領域。但同時，在當復雜的優化問題需要處理的時候，蜂群算法也存在很多問題，例如：收斂速度較慢、容易陷入局部最優等。為此，不少學者研究出了許多關于ABC算法的改進方法［3］。包括，雇傭蜂采取全局最優引導的策略，而且隨著實驗次數，引導程度相應減小，從而平衡全局和局部的搜索能力；提出在ABC算法中引入反饋機制，直接搜索最優解最有可能的位置，提高搜索效率［4］；Alam等在ABC算法中提出了，自適應步長機制，改進了算法性能；Aderhold等研究種群規模和蜜源位置更新公式在算法性能中的重要性，設計了兩種ABC算法［5］。

針對上述問題，本文提出了一種對比機制，即當種群初始化時，由于初始化的參數多而復雜，通過采取設置對比的方式［6］，可以在保證種群多樣性的前提下提高初始解的質量；同時，在蜜蜂搜索到各自的蜜源時，利用引入算法因子的方式，通過增加可以根據進化過程動態變化的因子來平衡蜂群算法的局部搜索和全局搜索能力，從而提高算法效率以及提升算法精度［7］。最后，根據仿真實驗和測試函數的數據對算法進行評測。

2 基本蜂群算法

人工蜂群算法，是一種較新的，屬于一類智能優化算法，基于模擬蜜蜂的采蜜過程提出，主要三個組成部分進行組成：食物源和雇傭蜂以及非雇傭蜂［8］。

食物源：代表蜜源。食物源下就是待求優化問題的可行解，是需要處理的基本對象［9］。食物源的好壞是通過蜜源大小評價的，即可行解的好壞是通過適應度來評價的。

雇傭蜂：又稱引領蜂，和食物源相對應，一個食物源就有一個引領蜂相對應，兩者的個數相等［10］；它的任務包括：發現食物源信息，一定概率的情況下與跟隨蜂分享信息；概率的計算通過人工蜂群算法中的選擇策略，通常根據適應度值以輪盤賭的方法計算。

非雇傭蜂：包含跟隨蜂與偵査蜂。跟隨蜂根據引領蜂提供的相關信息在蜂巢的招募區內選擇食物源［11］，而偵查蜂則在蜂巢附近尋找新的食物源。在人工蜂群算法中，跟隨蜂根據引領蜂傳遞的食物源信息，在此附近搜索新的食物源。若一個食物源在經過很多次后仍未被更新，則此引領蜂自動成為偵査蜂，尋找新的食物源代替舊的食物源［12］。

蜜蜂搜索操作由式（1）實現。

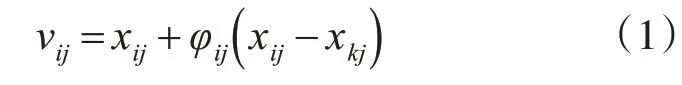
其中vij代表食物源位置，φij是［-1，1］中的隨機數，xij代表食物源第j維，xkj代表隨機選擇的不同于i的食物源的第j維位置［13］。式中，fiti為第i個食物源的收益率，隨著收益率越大，相應的食物源被選擇的概率也越大。

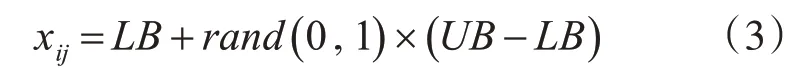
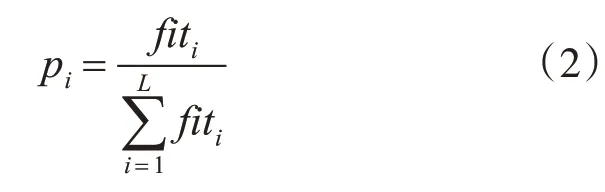
0，1內均勻分布的隨機數；LB和UB分別為問題解分量取值的下界和上界。故xi為某個食物源［14］。

同時，新解會根據下面式子計算適應度：

具體過程如圖1所示。

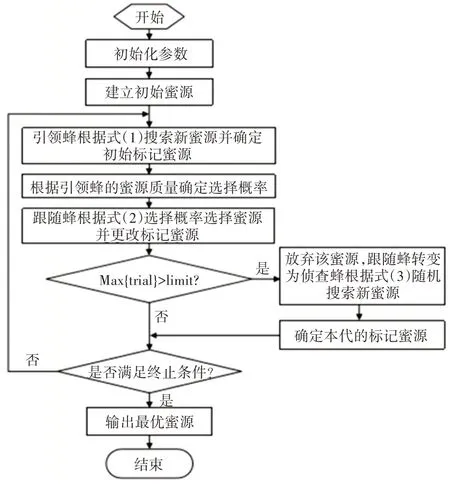
圖1 基本算法流程圖

3 改進的蜂群算法

本文針對收斂速度不快、會極大發生局部最優等問題，提出了在種群初始化和個體搜索方面改進之處。

3.1 對比機制

在種群初始化時，由于蜂群算法采取方式的隨機性，雖然在一定程度上體現了種群的多樣性，但不能夠保證初始解的質量［15］，對后面解的搜索易造成效率上的下降。所以，本文提出對比機制，即在初始化解的時候，對每個生成的個體進行M次迭代，這樣能夠達到質量更高的種群［16］。

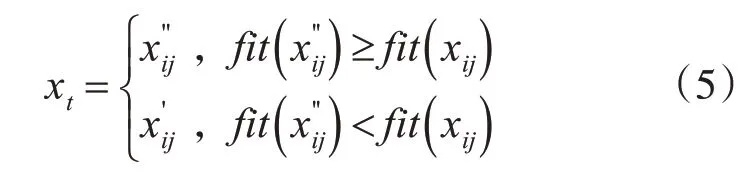
式子中，x'

ij表示個體前一次通過式（3）獲得的第j

3.2 算法因子的引入

在蜂群算法中，個體是通過搜索，然后根據共享的信息選擇最優解。但在這過程中，信息量會不斷減少，所以要考慮到全局優化和局部優化的作用［17］。因此，本文在優化過程中，引入算法因子，更好的提高了搜索的蜜源質量，即進一步篩選最優解的值，從而提高搜索能力。

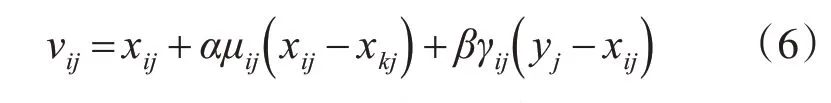
其中i為迭代次數，i∈[0 ，M]，μij是[- 1，1]之間的隨機數，γij是[ ]0，E一個隨機數，E是一個正數。yj第j維最優解的適應值。本文通過引入以上因子，在全局和局部兩方面［18］，都對搜索能力得到了相應的提高，正題優化了算法的性能，從而能夠在搜索的不同階段保證算法最優解。

3.3 CABC算法步驟

Step2：引領蜂根據式（1）搜索新蜜源，然后通過式（6）比較新蜜源，即適應度值。

Step3：之后跟隨蜂根據式（2）的概率選擇策略來選擇蜜源。

Step4：通過貪婪機制選擇更好的蜜源。

Step5：對于淘汰的蜜源，引領蜂根據式（3）轉換成偵察蜂。

Step6：記錄蜜源位置。

Step7：判斷能否滿足結束條件，如果滿足終止則輸出最佳解，否則回到Step2，直到達到limit值。

4 仿真分析

4.1 測試函數選擇與分析

本文為便于實驗仿真，采用以下四個基本函數進行算法性能比較。

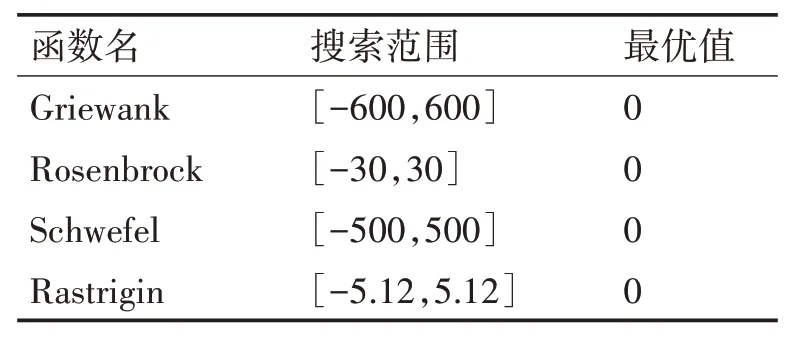
表1 測試函數

其中Schwefel為連續單模態函數，Rastrigin和Griewank為多模態非線性全局優化函數［19］，峰形呈現高低起伏的不定跳躍性，具有震蕩性，因此用來測試算法的搜索能力；Rosenbrock函數較為復雜，用于測試算法綜合性能［20］。

4.2 實驗評價標準

首先實驗設備為一臺64位PC機，算法是通過Matlab2014a軟件，用M語言實現。相關的實驗設置參數如下：種群數大小設為40，引領蜂個數和跟隨蜂個數各為20，最大迭代次數為1000次，判斷是否停滯的limit=100。

同時，為體現出算法的優化性能，每個測試函數獨立運行10次，記錄平均值、方差。

從圖2的四個測試函數運行結果看，基本ABC算法存在著收斂速度不快、收斂精度會比較低的問題。而改進后的CABC算法，Griewank、Schwefel、Rastrigin函數不僅收斂速度、精度和全局優化能力明顯優于ABC算法，即使對于Rosenbrock函數，CABC算法早期收斂速度快，后期趨于停滯，但整體性能明顯高于ABC算法。并且，由于CABC算法采取了對比機制，在運行初期階段，CABC初始解精度方面就明顯優于ABC算法，而且與最優值的差距明顯縮小，所需要的迭代次數也明顯減少。

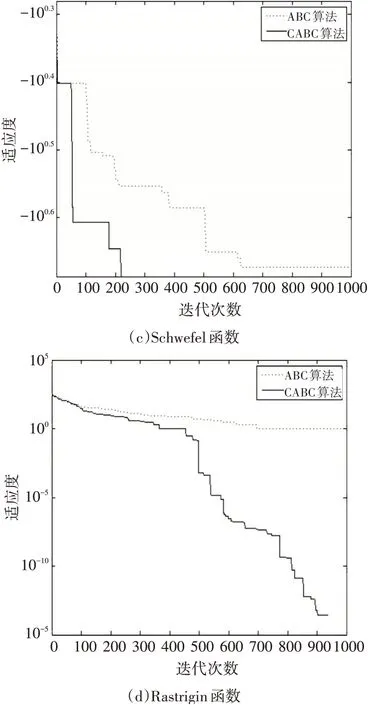
圖2 ABC算法和本文CABC算法的收斂曲線對比

整體而言，從以上的所有實驗分析可以得出結論，本文算法在性能上更加具有明顯的改進效果，說明改進的算法很好地改善了基本算法的存在會發生局部之最優的問題，也提高了解的精度。

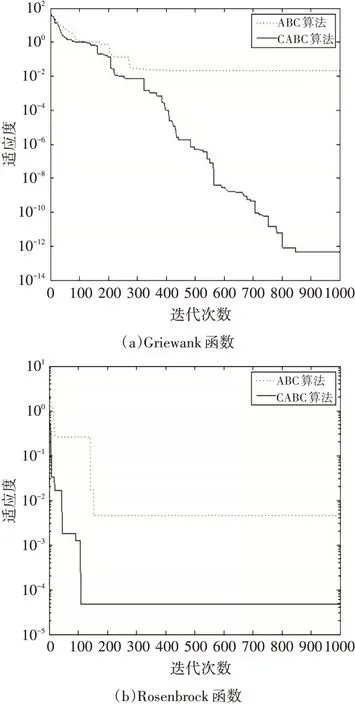
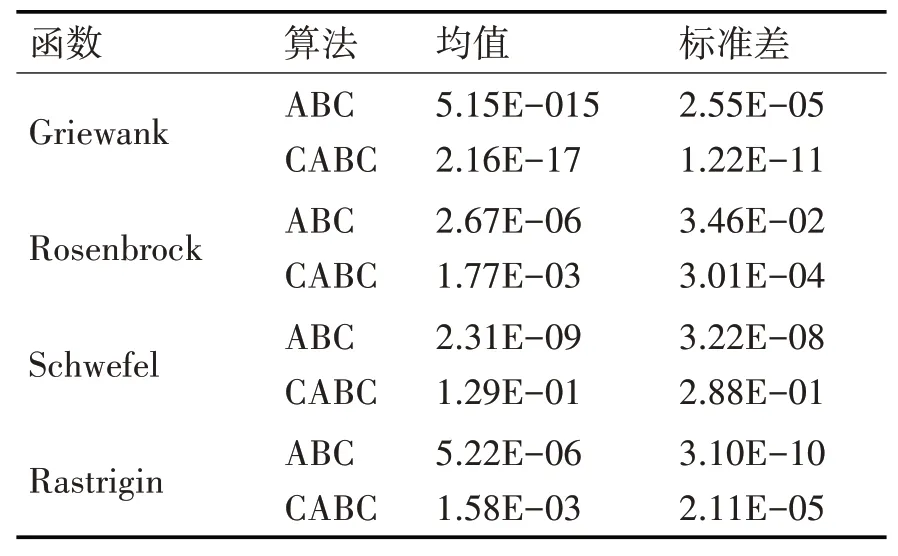
表2 四個函數實驗比較結果

5 結語

本文提出了一種改進的算法，通過在種群初始化的時候，加入對比機制，改善了解的質量，同時引入算法因子，更好的保證算法的搜索能力，從這兩個方面解決了原ABC算法易早熟的問題，提高了算法的全局搜索能力。由實驗的數據對比也說明了提出的算法在尋優精度和尋優效果上更好于原始算法。在今后的研究工作中，要集中于多目標優化問題和實際應用的研究上，更好地改善蜂群算法。