基于Herschel-Bulkley 流變模型的盾構螺旋輸送機保壓性能

楊益，李興高?，李興春，蘇偉林

（1.北京交通大學 土木建筑工程學院，北京 100044；2.城市地下工程教育部重點實驗室（北京交通大學），北京 100044；3.五邑大學 信息工程學院，廣東 江門 529020）

隨著我國城市軌道交通建設的快速推進，在實踐中土壓平衡式盾構穿越區的地質水文條件愈加復雜，這對盾構螺旋輸送機的排土、保壓及調壓作用提出了更高的要求.土壓平衡式盾構施工時要求開挖的土體通過螺旋輸送機以膏體的形式從壓力土倉輸送至盾構主機外的常壓環境中.在輸送過程中，渣土需要提供足夠的保壓能力來平衡螺旋輸送機兩側的壓力，以實現對土倉壓力的控制，進而保證開挖面土體的穩定.因此，準確預估其保壓性能對盾構安全掘進的控制起著至關重要的作用.

在螺旋輸送機內壓力分布特征的理論研究方面，Chung[1]假設作用在螺旋葉片及筒壁上的剪切應力為常數，得到螺旋輸送機沿程壓力梯度呈線性規律.Yoshikawa[2-3]分別假定渣土為摩擦型材料和塑性材料，依據提出的螺旋輸送機壓力梯度理論計算模型，得到了螺旋輸送機沿程壓力梯度分別呈現非線性和線性趨勢，并深入探討了不同轉速條件及不同幾何參數下的沿程壓力梯度分布規律.Talmon 和Bezuijen[4]假設渣土為均勻塑性糊狀介質，并且其剪切應力為常數，推導出螺旋輸送機壓力梯度具有線性分布的特點.隨著試驗手段的進步，通過模型試驗探究螺旋輸送機工作機制已成為可能.Peila 等[5]利用螺旋輸送機模型裝置，對泡沫改良中等粒徑砂土進行了排土試驗.Merritt 和Mair[6]針對黏土類渣土，利用螺旋輸送機模型進行了排土試驗，證實總應力沿螺旋輸送機呈線性分布的規律.Kim 等[7]通過模型試驗探究了螺旋輸送機的螺距、葉片角度及轉速等參數對出土量的影響.近年來，為進一步了解螺旋輸送機內渣土的運動狀態，渣土被假定為黏塑性流體用于數值計算中，為方便計算，目前常用的黏塑性流體模型為Bingham 模型[8-9].

綜上所述，雖然目前的研究成果已較為豐富，但現有理論模型中，關于螺旋葉片及筒壁上的剪切應力的假設尚存在爭議，而模型試驗存在操作難度大、成本高且流動狀態不可見等問題，因此，通過理論分析及模型試驗估計螺旋輸送機的保壓性能仍十分困難，數值手段成為解決該問題的新途徑.本文基于Herschel-Bulkley 流變模型（H-B 模型），探究了渣土流變參數及螺旋輸送機工作參數對螺旋輸送機保壓性能的影響規律，并通過模型試驗驗證了計算結果的準確性，以期為更好地解釋螺旋輸送機的保壓機制并準確預估及優化其保壓性能提供理論依據.

1 理論基礎

1.1 渣土流變模型

為滿足盾構施工時建立土壓平衡、防噴涌、防泥餅以及設備減磨的技術需求，開挖下來的渣土需呈塑性流動狀態[10].同時，合理的渣土狀態能為螺旋輸送機提供均勻的壓降梯度[9].近年來，隨著對塑性流動狀態的深入認識，渣土被認為是一種黏塑性流體[11-12].當剪應力小于屈服應力時，黏塑性流體表現出類似于固體的行為；但是，當超過屈服應力時，它將類似于流體流動[13].工程中常用的黏塑性模型包括Bingham 模型和H-B 模型.其中Bingham 模型最常見[14]，而H-B 模型由于其廣泛的適用性，常被用來描述新拌混凝土[15]、泥漿[16]、含顆粒懸浮液[17]等材料，其剪應力τ 與應變率的關系可以寫成：

式中：τ0為屈服應力；k 為黏度指數；n 為冪律指數.Bingham 模型是H-B 模型在n=1 時的特例.

孟慶琳等[12]通過自制的土體旋轉流變儀證實泡沫改良砂土的流變行為可用Bingham 模型描述.但除泡沫外，膨潤土和高分子聚合物也是常用的改良劑[18]，根據Yang 等[19]和Jeong 等[20]的研究，若土樣或改良劑中存在黏土成分，則其流變行為更符合H-B模型.因此，采用H-B 模型能夠更加準確地描述更多種類渣土的流變行為.

1.2 螺旋輸送機保壓原理

土壓平衡式盾構屬于閉胸式隧道掘進設備，開挖后的渣土經過改良形成良好的傳力介質，將來自千斤頂的推力傳遞至開挖面，用以平衡開挖面的土壓力ps和水壓力pw.螺旋輸送機有兩方面的作用：①從土倉內排出渣土；②通過渣土的運動使土倉壓力pe沿螺旋輸送機逐漸衰減，以實現保持土倉內壓力的穩定，即保壓作用；③通過調節轉速，控制出土量，調節土倉壓力pe，即調壓作用.圖1 所示為螺旋輸送機工作機制示意圖.

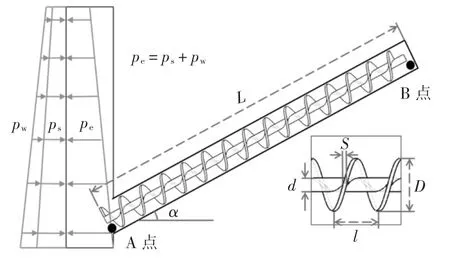
圖1 螺旋輸送機工作機制示意圖Fig.1 Working mechanism of screw conveyor

渣土壓力從螺旋輸送機入口A 到出口B 逐漸下降，在出口處降低為零或較小的量值，保證出渣過程穩定可控.假定渣土在螺旋輸送機內的流動連續且恒定，同時忽略渣土的壓縮性，則根據伯努利方程，圖1 中A 點與B 點的機械能應遵循：

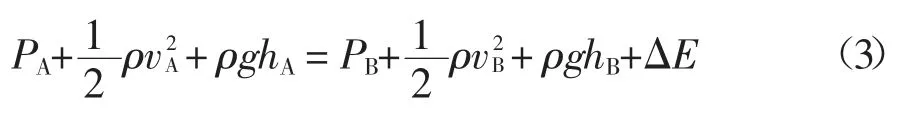
式中：P 為渣土壓力；ρ 為渣土密度；v 為渣土運動速度；h 為高度；ΔE 為機械能損失項.由于螺旋輸送出入口面積相等，因此，根據連續性原理，出入口的渣土速度vA和vB相等，公式（3）可變形為：

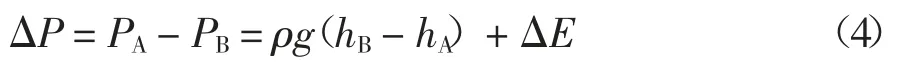
由公式（4）可知，螺旋輸送機的保壓能力來源于兩方面：①通過向上的輸送，將壓能轉化為重力勢能；②通過渣土的摩擦消耗，將壓能最終轉化為內能.ΔP 越大，則表明螺旋輸送機的保壓性能越優異.

重力勢能的大小取決于渣土的密度ρ 以及出入口的高度差hB-hA，高度差可根據螺旋輸送機長度L以及安裝角度α 計算：

渣土本身黏性摩擦力的存在是產生ΔE 的根本原因.若將螺旋輸送機內的渣土看作控制體，則ΔE可表示為：

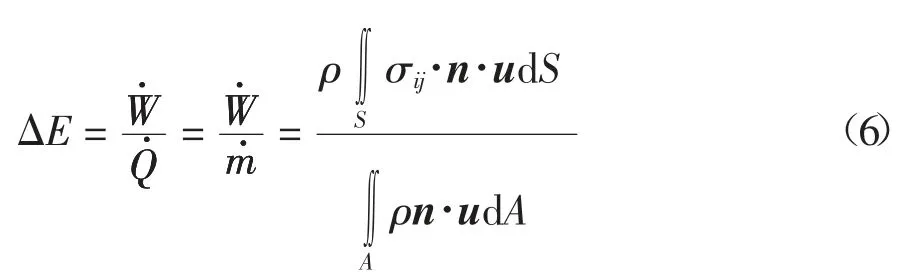
當忽略渣土壓縮性時，根據廣義牛頓內摩擦定律，應力張量σij與應變率張量sij的關系可表示為：

式中：p 為壓力函數；δij為克羅內克符號；μ 為渣土的動力黏度.

由公式（6）（7）可知，ΔE 由渣土的應力場及速度場決定.渣土的應力場與渣土材料本身的動力黏度μ 直接相關.但是，由于螺旋輸送機本身復雜的結構型式，無法通過解析方法求得ΔE，需要借助數值模擬的手段.在模擬過程中，μ 為非定值，可用H-B 流變模型進行描述：

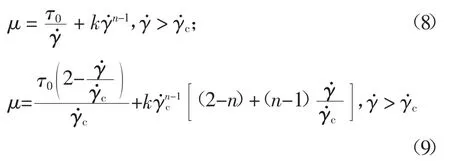
渣土的速度場則與螺旋輸送機的轉速及出渣效率有關.根據圖1 所示的螺旋輸送機的幾何結構，實際出渣體積流量為：

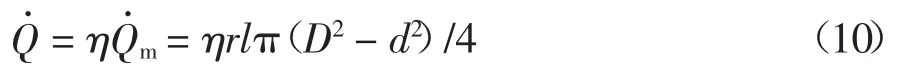
2 數值建模

2.1 計算模型及網格劃分

為盡量貼合實際，本文選取的計算模型為直徑6 m 的盾構機的螺旋輸送機模型.如圖1 所示的幾何結構，總長度L=10 m，螺旋直徑D=0.8 m，螺旋軸直徑d=0.2 m，螺距l=0.7 m，葉片厚度s=60 mm，共14節螺旋.采用Solidworks 軟件建立螺旋輸送機的三維幾何模型，并將其導入Fluent 軟件中進行網格劃分.模型采用多面體網格，由四面體網格轉化而成，在保證網格質量的基礎上，極大地提高了計算效率.整個流體域網格數目約為19 萬，網格密度如圖2 所示.

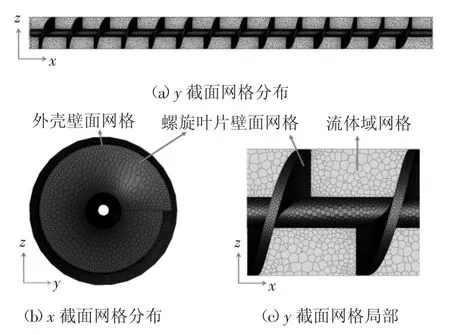
圖2 網格密度分布Fig.2 Grid distribution

由于數值建模的目的在于求解螺旋旋轉條件下渣土的機械能損失ΔE，模型中的螺旋葉片及流體域的網格均假定為勻速旋轉狀態，因此采用多重參考系法（MRF）對模型進行定常流計算.螺旋輸送機內的流體域設置為動區域，其他區域為靜區域；螺旋葉片為動壁面，外殼為靜壁面.動區域及動壁面按照螺旋輸送機轉速設置旋轉.

2.2 計算條件

本文算例選用層流模型，入口條件設置為壓力入口，壓力值為0.2 MPa，出口采用流量出口，流量值根據公式（10）計算，壁面均采用無滑移壁面條件，即默認渣土在壁面處與壁面的相對速度為零.內迭代步設置為300 步，可滿足殘差下降兩個量級.

由1.2 節的分析可知，影響ΔE 的因素來自兩個方面：①渣土的H-B 流變模型參數，即屈服應力τ0，黏度指數k，冪律指數n；②螺旋機工作參數：轉速r，出渣效率η.根據文獻[12，19]的流變試驗測試結果，表1 給出了不同類型的渣土流變參數的取值參考.計算參數具體取值見表2，所有工況中臨界剪切率均取0.01 s-1.轉速r 的取值則依據實際螺旋輸送機的設計工作參數.出渣效率η 為非人為調控參數，其取值可通過施工監測獲得，依據現有的報道[21-22]，本文中η 取值40%～100%，涵蓋了大部分的螺旋輸送機工作狀態.計算中考慮重力的影響，渣土密度為2 000 kg/m3，重力方向按照螺旋輸送機安裝角度α=20°進行設置.

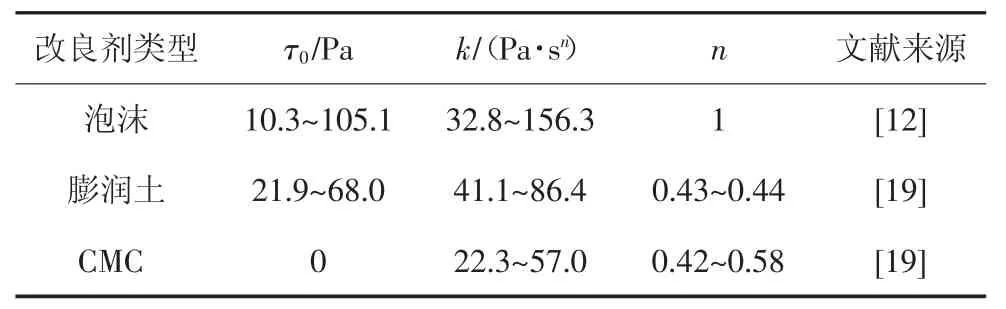
表1 渣土流變參數取值參考Tab.1 Reference value of rheological parameters

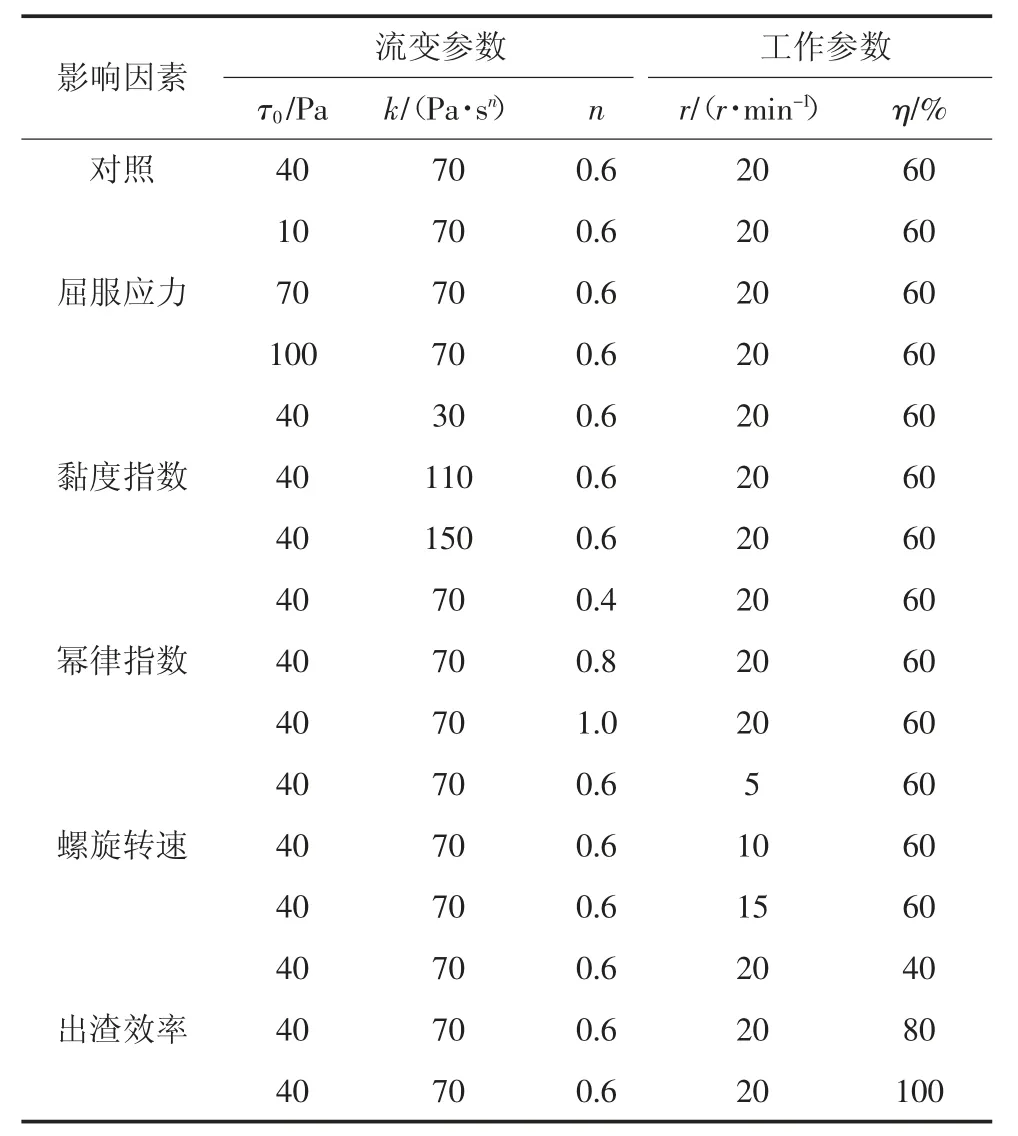
表2 計算工況Tab.2 Simulation cases

3 結果分析

3.1 渣土流動規律

以表1 中的對照組為例，計算結果如圖3 和圖4所示.圖3（a）（b）（c）分別為渣土的壓力、速度、剪切率分布云圖.

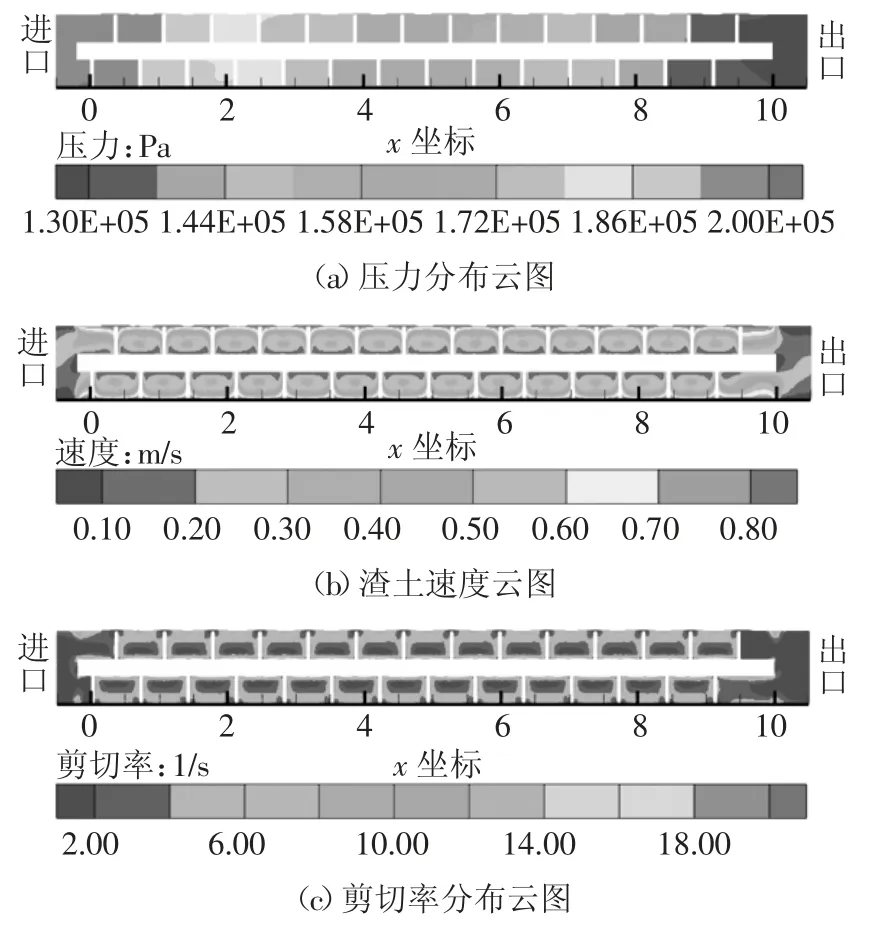
圖3 對照組渣土的計算結果Fig.3 Results of conditioned soil in control group

由圖3（a）可知，渣土壓力沿x 正方向遞減，螺旋輸送機內同一x 截面處壓力值相差不大.數值計算中的壓力為位置勢能與壓能的總和，因此進出口的壓差即為公式（3）中的ΔE，而非ΔP.由圖3（b）可知，螺旋輸送機內渣土的流動速度并不均勻，在螺旋葉片的帶動下，越靠近葉片外緣，渣土的流速越大，渣土流速的變化范圍為0～0.9 m/s.由圖3（c）可知，螺旋輸送機內渣土的剪切率并不恒定，由于渣土被假定為H-B 塑性材料，這意味著渣土內部剪應力隨螺旋位置產生變化.剪切率主要變化范圍為10 s-1以下，僅在轉軸附近局部超過10 s-1.

圖4 為螺旋葉片的壓應力、剪應力分布云圖.由圖4（a）可知，在旋轉狀態下，越靠近葉片外緣，剪應力越小，而葉片內緣及轉軸位置剪應力較大，每節螺旋葉片的剪應力分布基本相同.由圖4（b）可知，螺旋葉片的壓應力分布與圖3（a）中渣土壓力分布呈現相同的規律，壓應力沿x 軸線方向線性遞減.

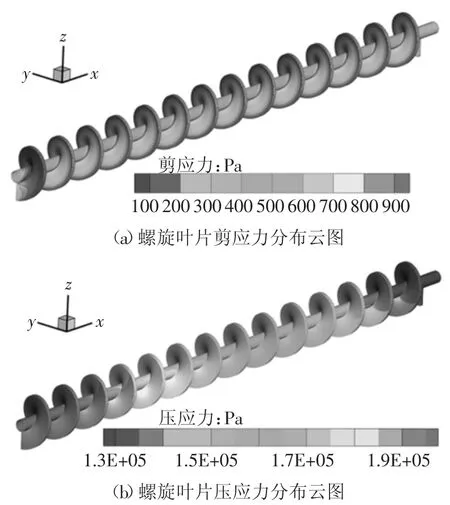
圖4 對照組螺旋葉片的計算結果Fig.4 Calculation results of screw in control group

3.2 渣土流變參數對保壓性能的影響

在螺旋輸送機轉速為20 r/min、出渣效率為60%的條件下，選取輸送機外殼某位置沿x 軸線方向的壓力變化為對象，探究不同渣土流變參數對保壓性能的影響.圖5（a）（b）（c）分別為屈服應力τ0、黏度指數k 及冪律指數n 對螺旋輸送機保壓性能的影響.由圖5 可知，輸送機外殼處壓力沿x 方向呈階梯狀下降的分布規律.由于螺旋葉片的阻隔作用，導致壓力在葉片位置產生明顯下降，形成階梯曲線的梯面部分；而在相鄰兩節葉片間的空隙處，壓力下降不明顯，形成階梯曲線的踏面部分.螺旋輸送機的壓降值越大，表明其保壓性能越優異.同一工況條件下，單節螺旋的壓降值相同，因此，增加螺旋輸送機的長度可提高螺旋輸送機的保壓性能.

從圖5 可看出，τ0、k、n 越大，壓力下降越顯著.其中，τ0每增加30 Pa，進出口壓差增加8.9 kPa；k 每增加40 Pa·sn，進出口壓差增加33.1 kPa；n 值越大，螺旋輸送機保壓性能的提升幅度越大.三者中k 和n值對保壓性能的影響較為明顯，而τ0的影響較小.因此，為提高螺旋輸送機的保壓性能，可通過渣土改良提高其流變參數中的k 和n 值.

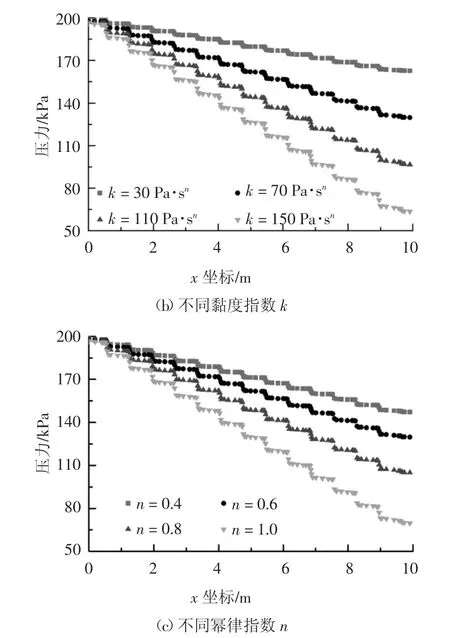
圖5 不同渣土流變參數下壓力隨x 坐標的變化Fig.5 Changes of pressure with x-coordinate under different rheological parameters of soil

3.3 螺旋輸送機工作參數對保壓性能的影響

當保持渣土流變模型參數恒定時，不同螺旋轉速r 和出渣效率η 對螺旋輸送機機械能損失ΔE 的影響規律如圖6 所示.由圖6 可知，螺旋轉速r 越大，出渣效率η 越高，則機械能損失ΔE 值越大，螺旋輸送機保壓性能越好.當η 固定不變時，隨著r 增加，ΔE 基本呈線性增加，但增長幅度略有下降.由此可知，在實際施工過程中，可通過提高轉速來增加螺旋輸送機的保壓能力.而當轉速r 固定不變時，隨著出渣效率η 增加，ΔE 也基本呈線性增加，并且r 值越高，ΔE 的上升幅度越大.在施工過程中，出渣效率η 并非人為可控因素，其大小與螺旋輸送機進出口壓差有關.當壓差較大時，進口處壓力推動渣土向外排出，此時出渣效率η 較高，渣土的機械能損失ΔE也較大，說明螺旋輸送機的保壓能力具有隨土倉壓力大小而自我調節的特點.

為更直接地表達ΔE 與r、η 間的對應關系，對圖6 中的計算結果進行二元多項式回歸，結果如圖7所示.由圖7 可知，二次多項式的回歸結果與計算數據的擬合優度極高，確定系數R2高達0.999；而一次多項式的回歸結果與計算數據的擬合優度相對略差，確定系數R2為0.970.為方便實際應用，一次多項式的回歸模型亦可滿足工程估測需要，即ΔE 與r、η 之間的關系可以表達為：

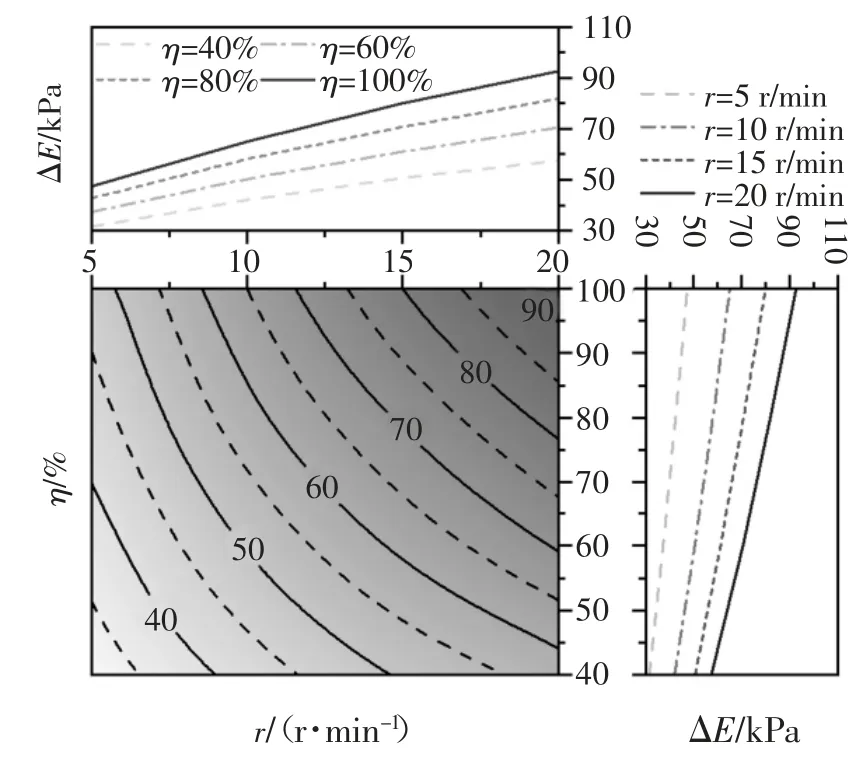
圖6 機械能損失ΔE 與r、η 的關系Fig.6 The relationship between ΔE and r，η

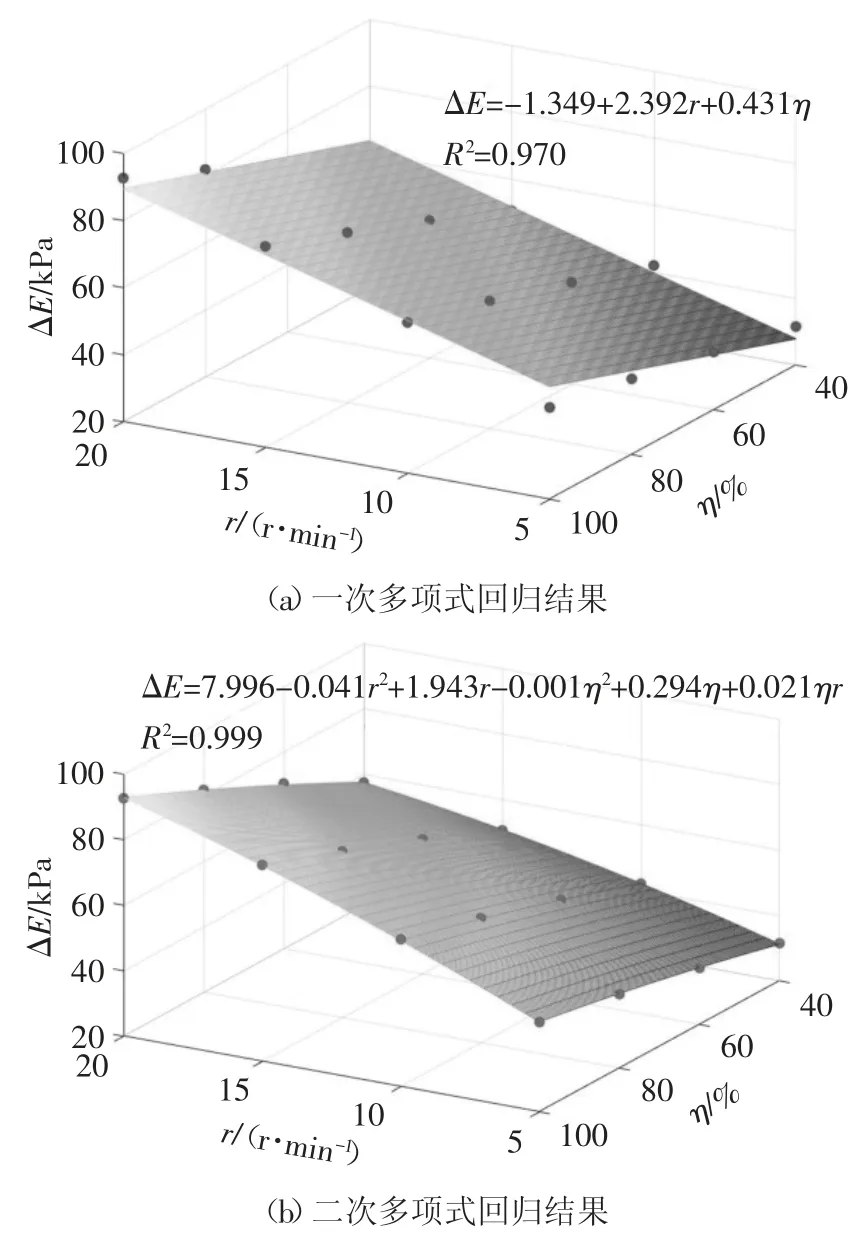
圖7 ΔE 的二元多項式回歸估測結果Fig.7 Results of ΔE by binary polynomial regression

由于渣土的流變參數保持不變，因此螺旋轉速r是通過改變渣土的速度場來影響機械能損失ΔE.螺旋轉速越快，渣土的運動速度越快，摩擦力做功越高，進出口壓差則越大.圖8 和圖9 分別為不同螺旋轉速下螺旋輸送機中心位置x 截面的流速與剪切率分布云圖.由圖8 可知，轉速5 r/min 和20 r/min 條件下渣土的流速具有相似的分布規律，在螺旋葉片的帶動下，越靠近圓筒外緣，渣土流速越高.但二者流速大小有明顯區別，轉速5 r/min 時最大流速僅0.2 m/s，而轉速20 r/min 時最大流速為0.8 m/s.由圖9可知，不同轉速下渣土剪切率的分布規律幾乎完全一致，剪切率大小與螺旋轉速大小成正比.由此可知，當螺旋轉速增加時，渣土的流速及剪切率隨螺旋轉速成比例增加，但由于公式（8）中H-B 模型的動力黏度μ 與剪切率之間為非線性關系，因此圖6 中ΔE 值不隨螺旋轉速r 增加而線性增長.

圖8 不同螺旋轉速下x 截面渣土流速分布云圖Fig.8 Velocity distribution of soil in x cross section under different screw rotation speeds

圖9 不同螺旋轉速下x 截面渣土剪切率分布云圖Fig.9 Shear rate of soil in x cross section under different screw rotation speeds

圖10 所示為不同出渣效率η 下x 截面渣土流速分布云圖.由于螺旋轉速r 相同，因此出渣效率η不同的成因是渣土的流速不同.由圖10 可知，隨著出渣效率增加，x 截面中出現月牙形的加速區，出渣效率η 越高，加速區越明顯.出渣效率η 的影響因素較為復雜，顯然僅依靠螺旋旋轉產生的“抽力”難以在渣土中心區域形成加速區，加速區是在土倉壓力的推動作用下形成的.當出渣效率在40%～60%之間時，加速區不明顯，此時渣土的輸送由螺旋旋轉主導；當出渣效率在80%～100%時，加速區明顯，此時渣土的輸送受螺旋“抽力”及進出口壓差共同作用.在實際應用中，出渣效率的確定可通過統計出渣量和螺旋輸送機轉速進行估計.

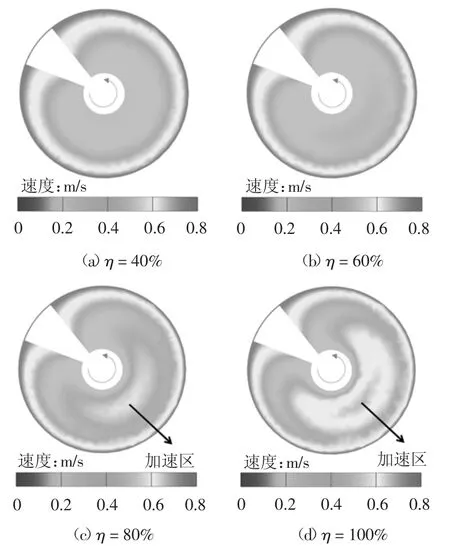
圖10 不同出渣效率下x 截面渣土流速分布云圖Fig.10 Velocity distribution of soil in x cross section under different soil conveying efficiency

圖11 所示為不同出渣效率下x 截面渣土剪切率分布.由圖11 可知，隨著出渣效率η 增大，渣土剪切率整體呈增大趨勢，局部區域出現明顯增大.其中，轉軸及外殼壁面附近剪切率增長最為明顯，最大剪切率始終維持在20 s-1以內.因此，在進行渣土改良時，應重點關注剪切率在0～20 s-1范圍內渣土的流變行為.

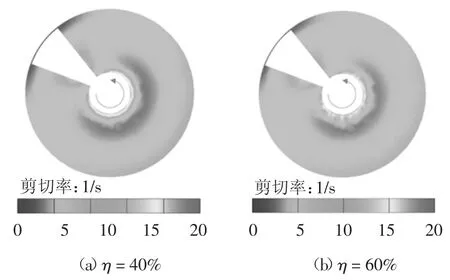
圖11 不同出渣效率下x 截面渣土剪切率分布云圖Fig.11 Shear rate of soil in x cross section under different soil conveying efficiency

3.4 螺旋輸送機保壓性能優化流程

根據以上分析，螺旋輸送機的保壓性能與渣土的流變行為及螺旋輸送機的工作狀態均密不可分.因此，在計算螺旋輸送機保壓性能時，需依據實際情況逐一判別，不可一概而論.圖12 提供了螺旋輸送機保壓性能的優化流程，流程詳細說明如下：

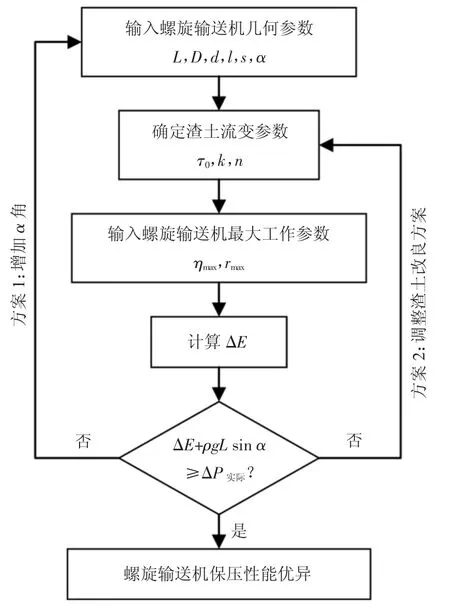
圖12 螺旋輸送機保壓性能優化流程Fig.12 Optimization flow chart of pressure maintaining performance of screw conveyor

1）確定螺旋輸送機的相關幾何參數以用于數值建模.若螺旋輸送機為雙節螺旋結構，則也應按實際尺寸建立幾何模型.

2）通過流變試驗確定隧道穿越地層所產生渣土的H-B 流變模型參數，由于隧道可能穿越多種地層，應分別對經渣土改良后的不同類型渣土進行流變測試，取所有結果中的最小參數值作為最不利工況.

3）確定螺旋輸送機的最大工作參數，其中最大轉速rmax應依據螺旋輸送機設計參數選取，而最大出渣效率ηmax宜取100%，當η 超過100%時，則可認為實際出渣量大于螺旋輸送機自身的輸送能力，此時螺旋輸送機保壓功能失效的風險將大大增加.

4）利用CFD 方法計算機械能損失ΔE.

5）若ΔE+ρgL sin α≥ΔP實際，即計算保壓能力大于實際螺旋輸送機進出口壓差，說明保壓性能優異.反之，則需要對保壓性能進行優化，方案1 為增加輸送機仰角α 值，若仍無法滿足判定條件，則需要采取方案2，調整渣土改良參數，如更換改良劑種類或調整改良劑用量，直至滿足判定條件.

4 試驗驗證

在數值計算中，渣土被假定為符合H-B 流變模型的假塑性流體，為驗證這一假定的可靠性，特將計算結果與室內試驗結果進行對比驗證.采用如圖13所示的螺旋輸送機模型試驗裝置，螺旋機長度1.0 m，直徑108 mm.模型機系統由渣土倉、傾斜螺旋機、聯軸器、減速電機、變頻器及水平方向加壓系統組成.其中螺旋機外殼處分別等間距安裝有6 個土壓力計和6 個空隙水壓力傳感器，如圖13 所示，用于測量法向應力和孔隙水壓力.在試驗過程中，當土倉內渣土逐漸減少時，加壓系統的水平方向氣缸以恒定壓力向前推進，氣缸始終與大型儲氣罐相連接，保證了螺旋輸送過程中土倉壓力始終維持恒定.根據土倉內渣土輸送情況，可計算出渣土的出渣效率η.

圖13 螺旋輸送機模型試驗裝置Fig.13 Screw conveyor model machine

由于模型試驗僅用于驗證理論計算中基本假設的可靠性，因此試驗中無需配置相似材料，試驗材料為經改良后的普通渣土，改良渣土的配比及相關力學參數如表3 所示.膨潤土漿液選用膨化24 h 的鈉基膨潤土漿液.改良渣土的塌落度值為190 mm，屬于典型的“塑性流動狀態”.根據文獻[19]所述的測試方法，采用Brookfield R/S+型流變儀的十字板型轉子系統VT-40-20 測試試驗所用改良渣土的流變參數.渣土的流變試驗結果如圖14 所示，采用最小二乘法進行擬合，分別得到Bingham 模型和H-B 模型的擬合曲線，其中H-B 模型的確定系數R2高達0.998，而Bingham 模型僅為0.937，說明在模擬渣土流變行為方面，H-B 模型更為精確.螺旋輸送機排出的渣土與試驗前的狀態基本一致，僅有少量膨潤土漿液析出.試驗共設置兩種工況：工況1 螺旋輸送機運行轉速為16 r/min，渣土倉工作壓力為200 kPa；工況2 螺旋輸送機運行轉速為6 r/min，渣土倉工作壓力為100 kPa.待盾構螺旋機模型工作狀態穩定后，根據渣土倉內的土樣體積及出渣口排出的渣土體積，計算出兩種工況下模型機平均出渣效率分別為79%和63%.

表3 改良渣土的質量分數及力學參數Tab.3 Mass fraction and mechanical parameters of conditioned soil

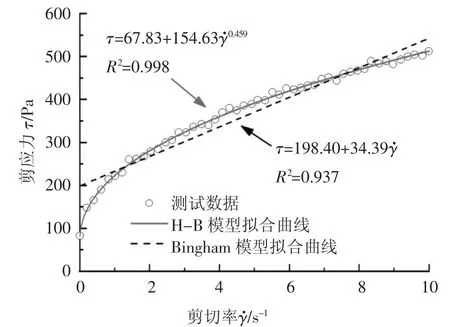
圖14 改良渣土的流變試驗結果Fig.14 Rheological test results of conditioned sand

依據模型試驗機尺寸及參數進行數值建模和計算，理論計算與試驗結果對比見圖15.整體來看，兩種工況下的理論計算結果與試驗結果均較為吻合，說明H-B 模型用于模擬螺旋輸送機內渣土的流動及力學性能是較為可靠的.工況1 中當x 坐標在0.6 m 和1.0 m 時，理論壓力值較實測值偏大，其可能的原因為，理論計算中假設渣土為均質的黏塑性流體，忽略了渣土與管壁的相對滑移，而實際渣土中的固體顆粒與管壁存在摩擦，增加了機械能的消耗.此外，當x 坐標為1.0 m 時接近螺旋輸送機出口處，兩種工況下的實測壓力值均存在突變，原因是螺旋機出口處突然泄壓導致實測壓力值較理論計算值更小，以致螺旋輸送機保壓性能的理論計算結果偏保守.

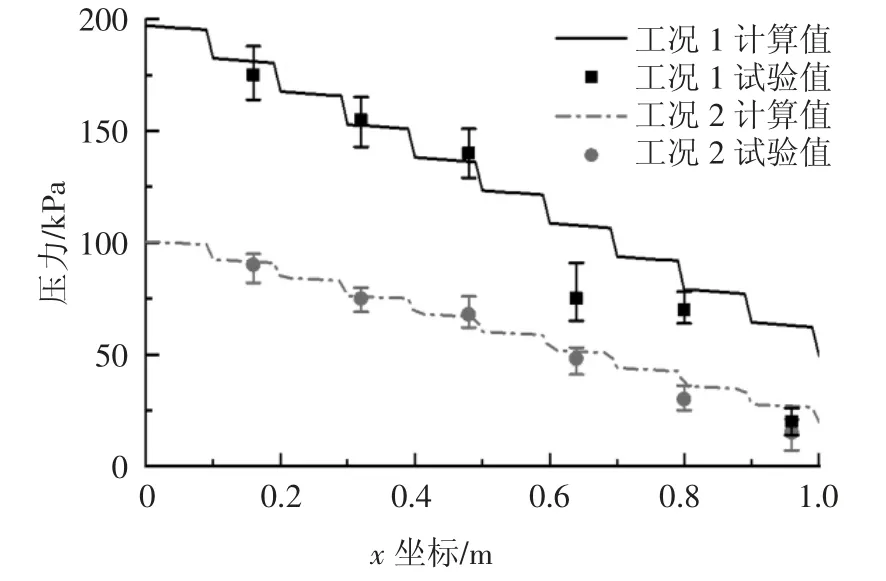
圖15 計算與試驗結果對比Fig.15 Comparison of calculation and experimental results

5 結論

1）螺旋輸送機存在2 個保壓途徑，一是將土倉內的壓能轉化為渣土的重力勢能，二是通過渣土的摩擦消耗，將壓能最終轉化為內能.重力勢能轉化量與螺旋輸送機的長度L 及安裝角度α 的正弦值線性相關，而因摩擦消耗產生的機械能損失ΔE 與渣土流變參數τ0、k、n 及螺旋輸送機轉速r、出渣效率η均密切相關.

2）采用CFD 方法在評價螺旋輸送機保壓性能方面有很大潛力.渣土的流變參數對螺旋輸送機保壓性能有較大的影響，其中H-B 模型的k 和n 值的影響最為顯著.k 每增加40 Pa·sn，機械能損失ΔE 增加33.1 kPa；n 值越大，保壓性能的提升幅度越大.

3）渣土摩擦消耗的機械能損失ΔE 與r 和η 基本呈線性關系，但隨著轉速r 增加，ΔE 的增長幅度略有下降.ΔE 與r、η 間基本符合一次多項式回歸模型，在本文選取的計算條件下，函數形式可表示為ΔE=-1.349+2.392r+0.431η.

4）通過數值模擬結果與試驗結果的對比，驗證了H-B 模型用于模擬渣土流動和計算螺旋輸送機保壓性能的可靠性.依據數值計算結果，給出了螺旋輸送機保壓性能的優化流程，以期為施工過程中提高螺旋輸送機保壓能力以及渣土改良參數優化提供指導和依據.