基于特征工程的重要節點挖掘方法

潘 侃，尹春林，王 磊，陳端兵,3*

（1. 云南電網有限責任公司電力科學研究院 昆明 650217；2. 成都數之聯科技有限公司 成都 610041；3. 電子科技大學大數據研究中心 成都 611731）

現實生活中的復雜系統（如交通運輸系統、生物系統）可以很自然地用圖表示，其中節點表示系統中的各個要素，邊表示要素之間的關系[1]。復雜網絡的研究逐漸從宏觀層面深入微觀層面[2]。節點作為系統中最小的元素，不同節點在系統中的地位是不同的。重要節點是指相比于網絡中其他節點，能更大程度地影響網絡功能的一些特殊節點。這種節點數量不多，但是其影響力卻可以快速波及網絡中大部分節點，如社交網絡中權威賬號的輿論引導，交通網路中重要路口堵塞導致交通系統癱瘓等。節點重要性排序[1]和相對重要節點的挖掘[3-4]對現實生活有著重要的指導意義。在網絡分析中，節點的重要性通常用中心性[5]來度量，其主要目的是為基礎網絡的每個節點分配一個實值，用于度量該節點對其他節點的影響力。目前已有不少成熟的節點中心性計算方法，主要分為兩類[3]：1） 基于網絡結構特征的指標和方法；2） 基于隨機游走的指標和方法。

基于結構特征的指標和方法主要根據其他節點與已知節點之間的網絡結構特征設計相對重要指標。這些方法通過捕捉節點之間的局部連邊信息或路徑信息，衡量節點的重要性。度中心性（degree）是最簡單的中心性度量方法，主要利用網絡節點的連邊信息刻畫節點的重要性。度中心性認為一個節點鄰居數目越多，該節點影響力就越大。但若節點在網絡中屬于核心位置，即使它本身度很小，也有較高的影響力。基于此，文獻[6]提出了基于K-殼分解（K-shell decomposition）的K-shell 中心性，該中心性將外圍的節點層層剝去，使處于內層的節點擁有較高的影響力。還有一些基于路徑的中心性計算方法，如節點的接近中心性（closeness）[7]考慮將節點與其他節點的測地距離之和的倒數作為節點重要性。而介數中心性（betweenness）[8]認為經過一個節點的最短路徑越多，這個節點就越重要。受到介數中心性啟發，流介數中心性（flow betweenness）[9]、連通介數中心性（communicability betweenness）[10]、隨機游走介數中心性（random walk betweenness）[11]和路由介數中心性（routing betweenness）[12]相繼被提出。除此以外，H-index[13]作為評價學者學術成就的權威方法，也能很自然地延伸到復雜網絡的重要節點挖掘任務中。

上述方法能夠很好地捕捉節點周圍的局部結構信息。除此之外，很多學者采用基于路徑和隨機游走的方法，利用整個圖的拓撲信息挖掘圖中的重要節點。在不考慮時間開銷的前提下，從初始節點出發將信息傳播出去，當隨機游走趨于穩定時，信息保留越多的節點越重要。特征向量中心性（eigenvector）傳播時不僅考慮節點的鄰居數目，也同時考慮每個鄰居節點的重要性。另外，學者們還提出了HITs[14]、LeaderRank[15]、PageRank[16]、Vote Rank[17]等 其 他全局游走的方法。總體而言，這些基于全局游走的方法計算成本較高，不能有效地應用于超大規模網絡。文獻[18]考慮四階鄰居，提出了局部中心性方法LocalRank，在時間復雜度和準確率之間找到了一個較好的平衡點。

雖然復雜網絡中檢測節點重要性的方法很多，但它們都試圖找到能反映節點重要性的某種因素。但節點重要性之所以不同，是因為不同節點周圍的結構是異質的[19]。因此，本文利用機器學習方法挖掘節點結構特征與節點重要性之間的關系。首先基于二步可達子圖的節點信息，采用特征工程中的特征提取、特征重構方法，提出能描述節點周圍信息的特征集合。再利用簡單的線性回歸模型（linear regression model）[20]，學習節點局部結構與節點重要性之間的關系。在13 個真實網絡中，將訓練所得模型與度中心性、介數中心性[8]、K-shell[6]、H-index[13]和DynamicRank[21]中心性進行了比較。實驗結果表明，本方法能更準確、更有效地識別出復雜網絡中對信息傳播影響較大的重要節點。

1 基于特征工程的重要節點挖掘方法

重要節點挖掘是網絡攻擊和信息傳播及控制等領域中的核心問題之一。網絡中的少數節點具有非常高的影響力。而造成網絡中節點重要性差異的根本原因是節點周圍的結構差異[19]。閉塞的局部結構會阻礙節點影響力的傳播，而好的局部結構會促進信息在網絡中傳播。

本文研究主要針對無向無權圖G(V,E)，其中V={v1,v2,···,vn}是 節點集合，E={e1,e2,···,em}是邊集合，n和m分別是節點數量和邊數量。為了提取和重構節點鄰居信息得到節點的局部結構特征，首先拓展兩個鄰居的定義。

定義1 二階鄰居

若網絡中節點u的一階鄰居定義為 Γ1(u)，那么節點u的二階鄰居可定義為：

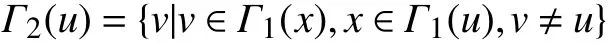
定義2 二階外聯鄰居

二階外聯鄰居屬于二階鄰居的子集，區別在于二階外聯鄰居是二階鄰居與一階鄰居的差集，定義如下：

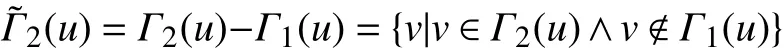
從局部角度考慮，節點的度以及節點鄰居的度最能反映節點的局部結構特征。除此以外，現有的中心性算法中，H-index 和K-shell 也是能較好反映節點重要程度的中心性指標。然而這些中心性指標對節點周圍復雜多樣的局部結構還是很難刻畫。

度中心性可以廣泛地概括簡單圖中重要節點的規律，一般來說，節點的鄰居越多，影響力越大。現實網絡中節點的局部結構非常復雜，單獨用某一種復雜網絡指標無法準確地刻畫節點周圍的結構信息。如圖1a～1d 中，節點A、B、C、D具有不同的局部結構，相應的中心節點的影響力也有差異，使用傳統的中心性方法無法準確區分這4 個節點的真實重要性。如采用度中心計算時，A、B、C、D屬于同一類型節點（dA=dB=dC=dD=2）。而Hindex 無法判斷節點A、C、D（hA=hC=hD=2）。另外K-shell 中心性也無法判斷A、B和C、D（kA=kB=1,kC=kD=2）。可以看出，傳統方法在節點重要性分析中還屬于粗粒度方法，對于不同的微觀局部結構有時很難區分。

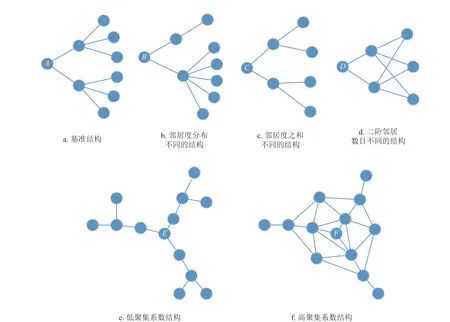
圖1 復雜網絡中節點的局部結構示例

1.1 特征提取

由于傳統的基于中心性的方法不能很好地刻畫節點的局部結構，特別是對于二階鄰居結構信息的刻畫過于粗糙。因此本文主要以節點的鄰居信息為基礎，提取和重組能刻畫節點局部結構的特征。

課堂中的所有元素都應該相互協同合作的，教師和學生作為課堂中的兩個參與者，師生之間的互動交流是不可缺少的。縱觀當前的高中英語課堂，教學氛圍比較壓抑，師生之間的交流不多，一般總是教師單方面的滔滔不絕的講述，學生沒有參與其中，只是被動的接受知識灌輸，實際上只有在師生之間友好交流的過程中，才能帶動學生參與學習，達到高效教學的效果，同時也增進了師生感情。因此，教師應該注重搭建師生互動平臺，在教學中要設計更多師生之間交流反饋的機會，比如可以開展小組合作學習，讓學生自主討論出一篇課文中比較難以理解的詞匯釋義或者句型語法，然后教師再引導他們進行解決，這有助于鍛煉學生的感知力和表達能力，真正實現師生協調發展。

1.1.1 一階鄰居特征

從一階鄰居開始，一般而言，度越大，信息越有可能傳播出去，因此，節點的度是刻畫信息傳播能力的一個重要特征。除此以外，一階鄰居度的分布一定程度上反映了節點二階鄰居的結構信息。如圖1 中，雖然節點A、B、C、D的度都為2，但是它們的一階鄰居度分布相差卻很大。特別地，A的一階鄰居度分布為[4,4]，而B的分布是[2,6]。顯然，A的一階鄰居度的分布更加均衡，而B的鄰居度分配不均衡。由于這兩個一階鄰居度的分布對應的局部結構不同，導致節點的影響力也不同。在低感染率下，鄰居度分布越均勻，信息往外傳播能力越強。若度分布極度不均衡，在圖1b 中，若度為6的節點沒有被感染，B節點的傳播能力會大打折扣。

為了描述鄰居度的分布均衡性，本文引入國際通用的，用以衡量一個國家或地區居民收入差距的常用指標：基尼系數（Gini coefficient），基尼系數最大為1，最小等于0。系數越大說明該分布越不均勻，系數越接近0 表明收入分配越是趨向平等。對給定的序列x=[x1,x2,···,xn]，該序列數據平均值為 μ，可采用下式直接計算序列的基尼系數：

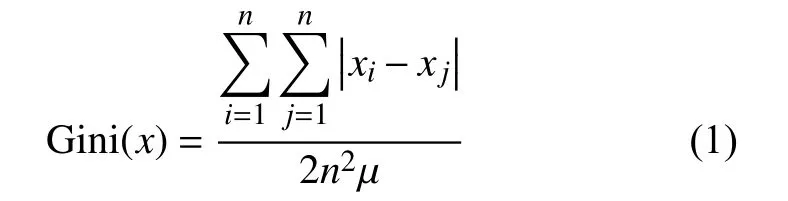
如圖1 所示，B的一階鄰居度的差距很大，而A的一階鄰居相對平衡。給定節點u，其一階鄰居為 Γ1(u)， 一階鄰居度的集合為D1(u)={dv|v∈Γ1(u)}。為了刻畫節點u的一階鄰居度分布的平衡度，定義節點u的一階鄰居度的基尼系數：

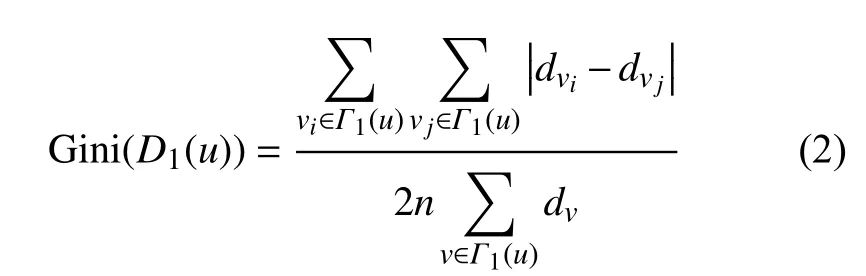
然而，只有基尼系數還不能完全反映節點一階鄰居局部結構。如圖1 中A和C，一階鄰居的基尼系數都為0 且中心節點的度都為2，僅靠這兩個特征還不能很好區分相同度節點重要性的差異，有時小度節點甚至比大度節點具有更高的傳播影響力。為了體現這種差異性，引入特征2 區分這種情況，特征2 為一階鄰居度之和，定義如下：

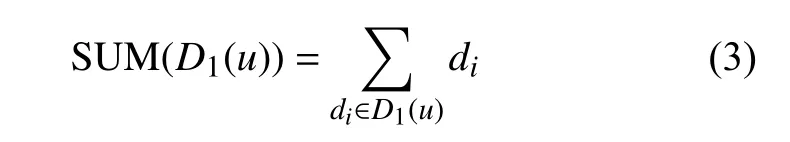
1.1.2 二階鄰居特征

有時僅用一階鄰居的特征還不能很好地刻畫節點周圍的局部特征，如圖1 中的節點A和D，Gini(D1(A))=Gini(D1(D))=0 且 SUM(D1(A))= SUM(D1(D))=0，僅從這兩個角度還是無法區別A、D兩種局部結構。針對上述情況，本文將二階鄰居數目作為特征，記為 Len(Γ2(u))， 其中 Len(Γ2(A))=6，Len(Γ2(D))=3。

在對一階鄰居的規模和分布進行分析后，將基尼系數和規模作為二階鄰居的特征。但與一階鄰居不同的是，一階鄰居與二階鄰居會出現重疊鄰居的情況。如圖1f 中的F節點，其周圍很多一階鄰居之間存在連接。在獲取二階鄰居時，很多一階鄰居還會被判定為二階鄰居。重疊的鄰居越多，節點聚集系數越大，節點的影響力在局部區域內能充分地傳播，但這種結構會導致信息很難再往外傳播[22]。如圖1 所示，在鄰居節點數目一致的情況下，E節點往外傳播的能力大于F節點。因此中心節點的二階外聯鄰居Γ ?2(u)度的分布和規模反映了信息從中心節點向外傳播的能力。基于此，本文提取二階外聯鄰居度的基尼系數和SUM 值作為節點的局部結構特征。

表1 節點局部結構特征度量

至此，本文從局部結構的規模和平衡性兩個角度，針對一階、二階鄰居，提取了共8 個特征，具體計算方法和描述總結在表1 中。除上述特征外，還有其他類型的特征對排序結果也有影響，如鄰居度的最大值、平均值、方差等。這些特征都會對節點重要性判斷帶來影響，本文僅作為一種算法思路，通過重構二階鄰居內的度信息，得到刻畫節點鄰居結構最主要的8 個特征用于節點重要性排序。

1.2 節點重要性學習建模

節點的重要性與節點周圍的局部結構有著緊密的關系。本文根據表1 列出的特征，采用線性回歸（linear regression）模型對節點局部特征與節點重要性關系進行建模。定義一個線性回歸函數f:x→s，將節點的結構特征映射為節點的相對重要性，具體可表示為：

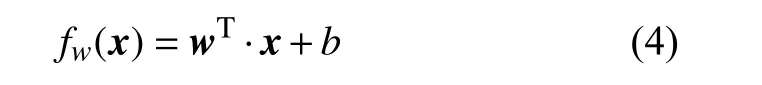
式中，w為特征向量的權重向量；x是特征向量；b是誤差項。

圖2 節點局部特征生成示例

至此，在獲得了節點v的歸一化結構特征xv和真實重要性sv后，采用線性回歸模型，選取均方誤差（mean squared error, MSE）建立目標函數以學習節點局部結構特征與真實重要性之間的關系：

為了獲得模型最優的回歸系數，本文采用Adam 優化器[27]優化目標函數。

1.3 模型訓練

本文用LastFM[28]作為訓練網絡對節點重要性挖掘模型進行訓練學習。LastFM 是一個2020 年3 月從公共API 收集的社交網絡，節點代表亞洲的用戶賬號，邊代表它們之間相互關注的關系，其節點規模為7 624，邊數量為27 806，最大度為216。首先從LastFM網絡中提取節點的特征向量；同時，以LastFM 網絡中每個節點為初始感染節點，進行1 000 次獨立的SIR 傳播仿真，將1 000次的平均sv作為每個節點的標簽；最后，將標簽和特征向量作為訓練集輸入線性回歸模型，訓練得到節點重要性度量模型，用于預測其他網絡中每個節點的重要性。

2 實驗與討論

本文用13 個不同類型的真實網絡對本文提出的方法進行測試，并和度中心性、介數中心性、Kshell 中心性、H-index 中心性和DynamicRank 中心性進行對比。

2.1 評估指標

2.2 數據集

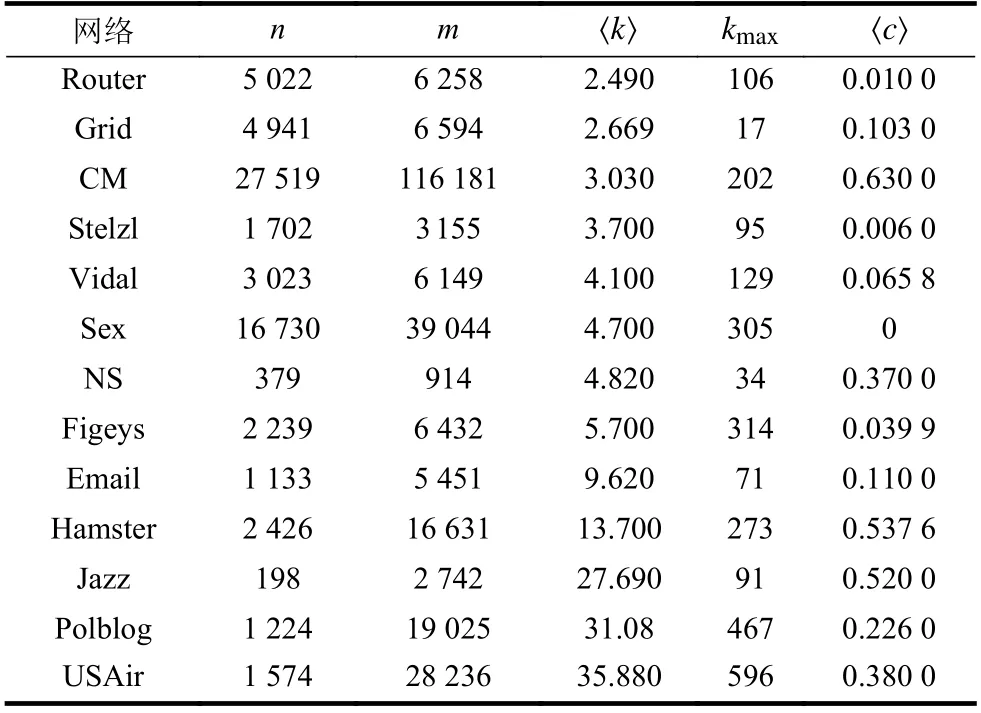
表2 13 個真實網絡的基本特征數據

本文采用的13 個真實網絡中，包括了規模較小的網絡（如Jazz），也有規模較大的網絡（如Cond-Mat, CM），其平均度的范圍為2～35。其中，1） Jazz 是爵士樂手之間的協作網絡，每條邊表示兩個樂手在一個樂隊中一起演奏；2） NetScience（NS）是發表關于復雜網絡主題論文的科學家之間的合作者網絡；3） Email 是Rovirai Virgili 大學成員之間的電子郵件交換網絡；4） Sex 是研究男女性伙伴的網絡；5） Polblog 是2004 年美國大選中博客之間的超鏈接形成的網絡；6） USAir 是2010 年美國機場之間的航空網絡；7） Router 是由Rocketfuel 項目收集的互聯網路由器拓撲網絡；8） Cond-Mat（CM）是1995 年-1999 年arXiv 出版物的科學家合作網絡；9） Grid 是美國西部的某電力網絡；10） Figeys、Stelzl 和Vidal是3 個蛋白質-蛋白質相互作用網絡；11） Hamster是一個包含網站用戶之間的友誼和家庭關系的網絡。以上數據集可從網站（http://konect.cc/networks/）獲得，這13 個真實網絡的詳細特征如表2 所示，其中，n是節點數目，m是邊數目，表示所有節點的平均度，kmax代表節點的最大度，所有節點的平均聚集系數為。

2.3 實驗及分析

為了檢測模型預測的準確性，本文首先對測試網絡中每個節點作1 000 次SIR 傳播仿真，將1 000次的平均sv作為測試網絡節點的真實影響力。再根據節點影響力的預測值和真實值的Kendall Tau 系數評價模型的預測效果。本文方法和其他基準方法的對比結果如表3 所示。

從表3 可以看出，本文提出的方法在大部分網絡中表現非常好，13 個網絡中有10 個網絡都好于對比方法，尤其在NS 網絡中，相比于表現第二好的DynamicRank 中心性方法，相關系數提升了0.2456。在平均度比較高（平均度大于20）的網絡中，由于訓練集中缺少類似的大度點的局部結構，無法學習到大度節點的重要性，極大影響了模型的判斷，如在Polblog 網絡中，最大度為467，遠高于訓練網絡的最大度216。另一方面，平均度反映網絡中常見的局部結構。如訓練網絡LastFM 的平均度為7.294，雖然也存在度為20 的局部結構，但這種結構在訓練網絡中并不常見，轉換得到的訓練集會極不平衡。模型對度為20 的局部結構無法充分學習，因此模型在度大于20 的網絡表現也就較差。

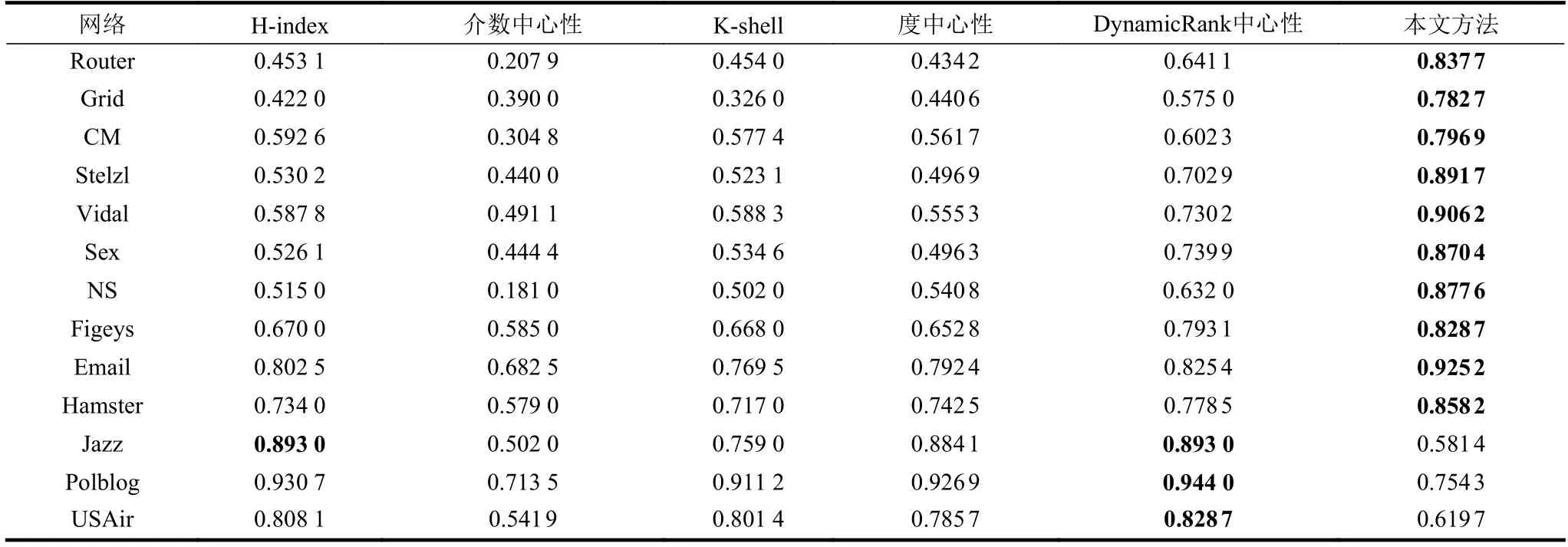
表3 不同方法與SIR 模型仿真結果的Kendall Tau 相關性系數

為了驗證本文學習模型的魯棒性，本文在不同感染概率下對模型效果進行了分析。設置 β=cβc，選取不同c值用于分析選取不同傳染概率對重要節點挖掘的影響。

如圖3 所示，在不同感染概率β=βc、1.5βc、2βc、2.5βc下，本文利用特征工程的方法提出的特征能夠很好地描述節點在網絡中的重要性。在不同的感染概率下，本文方法依舊能在低平均度的網絡中取得最好的效果。圖3 的結果表明，雖然基于特征工程的方法在訓練時依賴于感染概率，但訓練得到的重要性評估模型對感染概率并不敏感，適用于對不同感染概率下，節點重要性的挖掘。

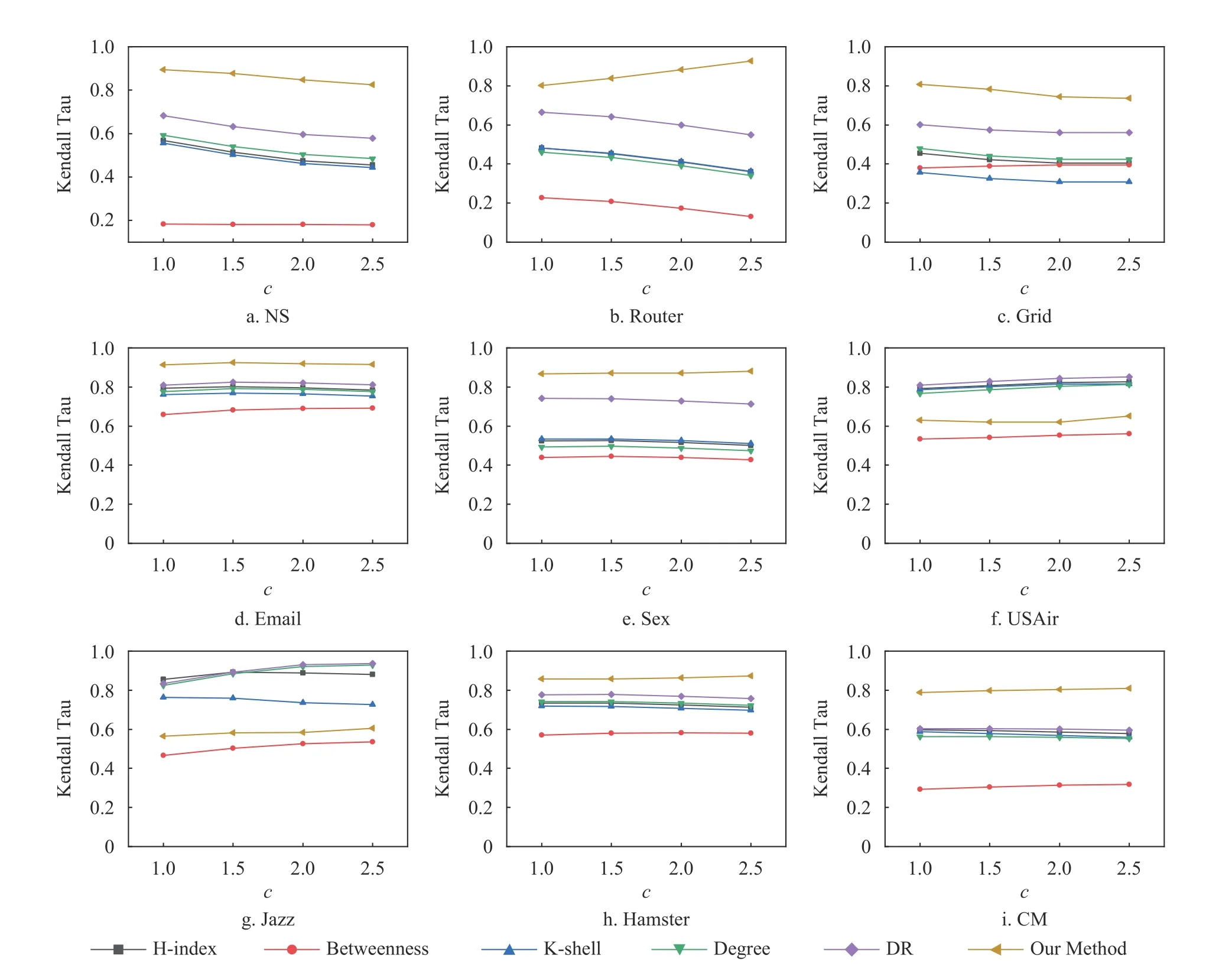
圖3 本文方法與其他基準方法在各網絡中不同感染概率下的Kendall Tau 相關性系數對比

進一步，為了驗證這8 個特征的有效性，本文在不同網絡上選取不同特征組合進行實驗分析。

1） 在Figeys 網絡中去除特征1 后，算法排序結果和實際仿真排序結果的Kendall Tau 相關性系數從0.83 下降到0.77。

2） 在NS 網絡中去除特征1 后，Kendall Tau 相關性系數從0.879 下降至0.872，若去除特征2，Kendall Tau 相關性系數下降更為明顯，降至0.861。

3） 若在Grid 網絡中去除特征2，Kendall Tau相關性系數從0.775 下降至0.728。若再進一步去除特征7，Kendall Tau 相關性系數大幅降低至0.688。

4） 在Stelzl 網絡中，若同時去除特征3 和7 時，Kendall Tau 相關性系數從0.89 大幅下降至0.79。

從上面的分析可以看出，8 個特征在不同網絡的重要節點排序上相互補充和促進，去掉某個或某組特征，對節點重要性研判將帶來直接影響。而完整的8 個特征，模型更穩定，也能更準確地判斷網絡中節點的重要性。

同時，根據信息傳播理論，節點對三階鄰居以外的影響已經很小，更高階的鄰居信息趨于同質化[30]。為了驗證更高階鄰居對模型的影響，根據特征4-8，拓展三階鄰居的特征9-13（三階鄰居的度之和、三階鄰居數目、三階鄰居度的基尼系數、三階外聯鄰居度之和、三階外聯鄰居度的基尼系數）。選取email 作為測試網絡，發現8 個特征訓練所得模型的排序結果與仿真結果的Kendall Tau 相關性系數為0.925，而13 個特征的相關系數為0.927，提升并不明顯。實驗表明，選取二階鄰居以內的信息已足夠。

3 結 束 語

本文利用特征工程方法對節點的鄰居信息進行提取和重構，提取更能反映節點局部結構的特征向量。根據節點的局部結構特征信息，建立了用于挖掘網絡中重要節點的機器學習模型。用13 個實際網絡對本文所提方法的有效性進行了測試，并和典型的基準方法進行了對比。實驗結果表明，本文提出的機器學習模型能有效地挖掘網絡中的重要節點，13 個網絡中有10 個網絡的效果顯著地優于已有方法。由于本文方法一定程度上依賴于訓練網絡的局部結構，對于訓練數據中出現較少的局部結構，由于訓練不充分，在測試時表現出的效果整體欠佳。在未來的研究中，一方面是構建更加豐富多樣的訓練集，另一方面，需提取更為豐富的局部特征，提升模型的預測能力。近年來，隨著深度學習的發展，尤其是圖神經網絡的研究深入，如何利用圖神經網絡訓練泛化性能更好的復雜網絡局部結構特征的表達模型[31]，從而提高重要節點識別的準確率也是一個重要的研究方向。