指向數學關鍵能力培養的深度思考實現路徑

陳賽

摘? ?要：深度思考是數學課堂的靈魂，是培養學生數學關鍵能力的核心要素。要培養學生數學關鍵能力，教師就需要從引發學生深度思考的角度設計和實施教學，通過創設有思考價值的問題情境，開展思行結合的自主探索，實施有教師指導的合作交流，展開有梯度的引導質疑等路徑促進學生深度思考。

關鍵詞：小學數學;深度思考;數學關鍵能力;核心素養

中圖分類號：G623.5? ?文獻標識碼：A? ?文章編號：1009-010X（2021）28-0031-03

數學關鍵能力是數學核心素養的核心成分，它主要包括運算能力、空間觀念、推理能力、抽象能力等等，培養數學關鍵能力是數學核心素養培育的重點，也是數學課堂教學的重要任務。因此，一線數學教師要在培養學生的關鍵能力時，讓學生反復經歷從事物的外部現象逐步深入事物內部本質層面，掌握知識的核心概念，并運用概念和深化概念的過程。在這個過程中深度思考，促進學生更深入地理解、溝通知識間的聯系，建立起良好的知識結構，同時形成數學關鍵能力。可以說，深度思考是數學課堂的靈魂，它貫穿高效課堂的始終，是培養學生數學關鍵能力的核心要素。在數學教學中，教師要創造有利于啟發學生深度思考的場域，讓學生在深度思考中培養數學關鍵能力。

一、深度思考源于情境——創設有思考價值的問題情境，讓思考從模糊走向清晰

（一）營造情景體驗場，開啟深度思考的閥門

小學生注意力容易被有趣的問題情境吸引。在教學時教師要密切聯系學生的生活經驗，創設具有思考價值而又有趣的問題情境，讓學生在認知沖突中激發探索問題的興趣，開啟深入思考的閥門。

在教學“分數的初步認識”時，教師創設了豬八戒吃餅的故事情境：豬八戒到一個農民家里要餅吃，吃了三個餅，還沒有吃飽。接下來，豬八戒想好了一個形狀，但不知如何表達，只是說“我只要一小塊兒”。教師適時問道：“一小塊兒究竟是多大呢？”，學生默想一會，接著出示3張同樣大的圓形紙片，讓三位學生上來撕一撕。經過比較同學發現，雖然都表示“一小塊兒”，但是三位學生撕的形狀有別、大小不一。為什么會這樣？

（二）設置問題驅動鏈，建構個性化知識結構

深度思考使他們不斷地找出有聯系的信息并進行整合、遷移、轉化，讓思考逐漸從模糊走向清晰，最終完成個性化的知識建構。

思考后他們明白了由于“一小塊兒”說的太模糊了，表達不清晰，加上每個人對一小塊兒的理解不一樣，所以撕出來的紙片大小也不一樣。緊接著，教師再出示一個圓形圖，平均分成四塊，其中一份涂上顏色，這時教師問：“你能夠用精確的語言或者用一個數，把現在涂色的這一塊表示出來嗎？”學生陷入了深度思考。

認識分數，是數概念的一次拓展，對于三年級學生而言，難度較大，但教師呈現豬八戒要餅的問題情境，讓學生置身于認識的沖突與困惑之中，從而感受到這“一小塊兒”不能再用原來學過的數表示，必須用一種新的標準或者數來表示。當出示“一小塊兒”圖形后，學生們得以從不同的視角去解釋，表達對一小塊圖形（就是四分之一的圓）的認識與理解。這個學習情境中，既有動手操作，也有比較分析，同時貫穿著學生積極的深度思考，達成了理性與感知的對接。學生認識由原來的模糊，經過點撥和引領，學會了從數學的視角去觀察和思考，從而逐漸接近分數意義的核心部分，走向數學化的清晰。

二、深度思考融于探索——開展思行結合的自主探索，讓思考從片面走向全面

把思考融入到動手操作和自主探索中，能夠促進學生在體驗中從感性走向理性，結合具體的分析問題、探索問題和解決問題的過程，逐漸地打開思路，在已知和經驗基礎上，不斷完善知識網絡，形成良好的知識結構。在不斷的甄別、論證、探索過程中，他們的思考也會由片面走向全面，合情推理能力得到有效提升。

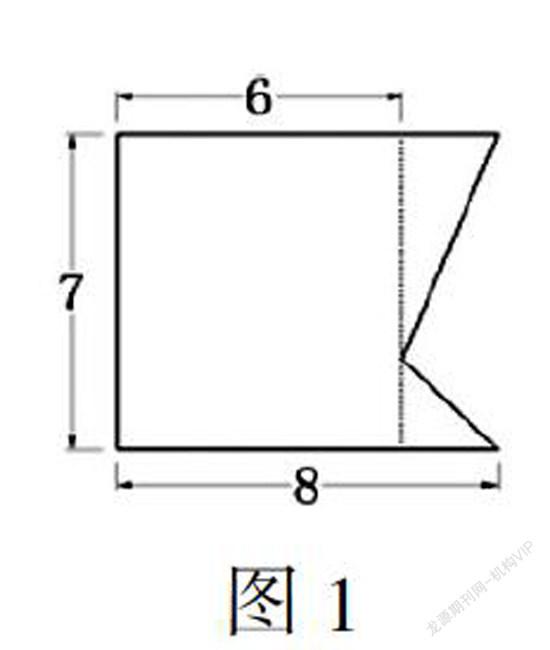
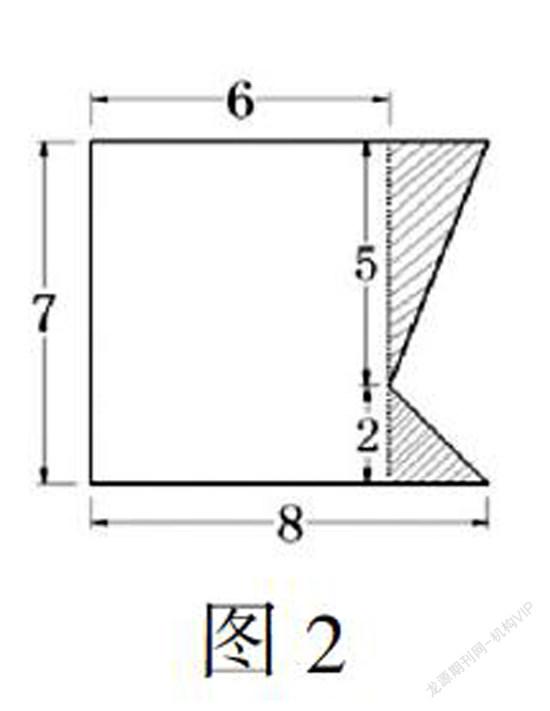
在計算下面圖形（單位厘米，如圖1）的面積時，學生先獨立嘗試計算，小組交流后匯報。匯報中出現了很多不同的算法，其中一種把圖中右下角的小三角形看成底和高都為2厘米的等腰直角三角形來計算（如圖2），教師提出質疑：這種做法結果是對的，但是有沒有道理呢？

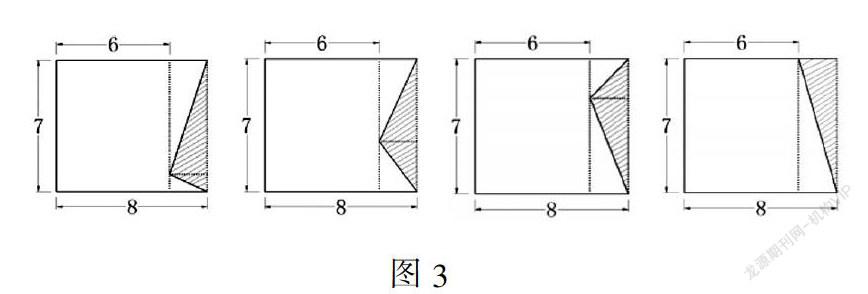
在辯論和深度思考中，學生借助畫圖和列舉，計算發現了下面的小三角形高即使不是2厘米，而是3厘米、4厘米或者5厘米，結果面積都一樣。還有學生出示了以下幾個圖形（如圖3～6），并介紹：如果增加一條輔助線，兩個三角形和涂色部分正好組成了一個小長方形。這樣，不論把涂色三角形的頂點移到哪里，涂色大三角形面積都與兩個小三角形面積的和一樣多，涂色部分三角形的底和高是不變的，它的面積是組成的長方形面積的一半。

學生通過自己動手實踐，親歷了探究和論證一個與眾不同做法的對與錯。從把小三角形看成高是2厘米的片面認識中，通過列舉和畫圖的辦法逐步發現各種不同圖形中的內在聯系，借助直觀操作把復雜的問題簡單化，讓思考從片面走向全面，在這樣的教學中，學生不僅能夠提高解決問題的能力，還能夠發展他們的幾何直觀與合情推理能力。

三、深度思考精于對話——實施有教師指導的合作交流，讓思考由無序走向合理

教師指導下的交流對話能夠讓學生互相分享體驗、交流感悟，從而產生智慧的碰撞。面向全班的展示匯報，能夠示范好的做法，也能夠暴露出學習中存在的障礙，讓教師及時了解和掌握學生的思維狀況，然后根據學情及時點撥引導，有的放矢地持續推進學生對問題的思考，讓學生的思考從無序走向合理，在自我建構整體知識結構的過程中培養學生關鍵能力。

教學“解決問題的策略——列舉”時，在學生自主學習階段，有的學生把題意理解錯誤，把“用22根1米長的小棒圍成一個長方形”理解成一個長加一個寬就等于22米;也有的只畫了幾個長方形，并沒有列舉完全，就在畫的圖形中選出最大的一個面積作為結果;還有的學生知道周長一定的時候，長和寬最接近時面積最大，一步想到最大的長方形長6米，寬5米。總之，大部分學生還只停留在問題解決的表層，并沒有深入地去思考該如何更合理有效地解決類似問題，也沒有激起用列舉方法去解決這類問題的需求，更沒有思考如何列舉才能夠既不重復，也不遺漏。

在匯報展示環節，教師有意識安排學生從錯誤到正確，從重復遺漏到完整全面，從無序到有序來依次匯報。在匯報過程中，教師針對學生出現的思路上無序、混亂等問題，適時地加以引導、追問、點撥，幫助學生體會和理解，從而明確這類問題該如何進行思考，如何避免重復和遺漏，使學生的思考逐漸地由無序散亂走向有序合理，從而真正體會到一一列舉的價值。

四、深度思考深于質疑——展開有梯度的引導質疑，讓思考由膚淺走向深刻

教學中教師通過主問題+問題串的方式，對核心問題展開有梯度的質疑，引導學生專注于核心問題去靜思反省，讓學生經歷猜測、比較、判斷、甄別、感悟等深度信息加工過程，促進思考由膚淺走向深刻，從而深入到數學靈魂深處，感知到數學思想，體悟到數學方法，培育學生的關鍵能力和思維品質。

在教學“分數的初步認識”的練習環節中，教師先出示平均劃分好份數的長條（圖4），先讓學生說出其中涂色部分占這根長條的幾分之一，然后出示沒有顯示分成幾份的長條、（圖5），鼓勵學生猜測。在猜測時，由于受到慣性思維影響，大部分學生會認為是六分之一。這時教師采取一系列質疑追問來幫助學生建立數感：這個分數確定是六分之一嗎？有沒有其他可能？為什么？如果接著再往下分，就這樣一直分下去，分到的數會越來越接近哪個數呢？

在圖形演示和問題串的一再追問之下，學生關注于涂色部分的變化，逐漸地發現了變化的趨勢，想到如果一直分下去，分到的分數會逐步變小，直至小到無限地接近0，但又不是0，這時學生就會對極限思想有一種切身的體驗和感悟。這樣的追問不僅激發了學生刨根問底的欲望，也激活學生的思維，讓其在深度思考中領悟到數學思想方法的奧妙，在探究知識的過程中積淀了數學思想方法，培養了數學關鍵能力。

總之，在以培養學生核心素養為教育總目標的背景下，教師要從引發學生深度思考的角度設計和實施教學，創設具有思考價值的問題情境，去開啟學生深度思考的閥門，讓學生的思考在自主探索、合作交流、質疑提升的過程中逐步深入，從而想得更清晰、更全面、更深刻、更合理，有效地提升他們的關鍵能力和思維品質。