形式三角矩陣半環的自同構與反自同構

張源野， 譚宜家

福州大學 數學與計算機科學學院，福州 350108

半環理論是代數理論研究的一個重要內容，應用很廣泛[1-4]．半環上的自同構和反自同構是半環理論中的最基本的研究內容之一．對于自同構，文獻[5]證明了交換環上嚴格上三角矩陣代數的自同構可以表示成一個對角自同構、一個中心自同構和一個內自同構的乘積；文獻[6-11]研究了矩陣環和矩陣代數的導子和自同構．文獻[12]探討了形式三角矩陣環的導子和自同構．文獻[13]研究了形式三角矩陣環的反自同構．

本文在上述基礎上進一步研究形式三角矩陣半環的自同構和反自同構，所得結果拓廣了文獻[12-13]的重要結論．

定義1[1]一個半環是一個代數系統(R，+，·)，其中(R，+)是一個帶有恒等元0的交換幺半群，(R，·)是一個帶有恒等元1R的幺半群，乘法對加法滿足左右分配律．同時，對于任意a∈R，0a=a0=0．0≠1R，元素0，1R分別稱為半環R的零元和單位元．

設R是一個半環，如果對于任意a，b∈R，由a+b=0可推出a=b=0，則稱R為零和自由半環[1]或反環[14-15]．設a∈R，如果果a2=a，則稱a為一個冪等元．顯然0，1都是冪等元，稱為平凡冪等元．

設(R，+，0)是一個交換幺半群，a∈R，如果存在b∈R，使得a+b=0，則稱a為一個可反元，此時b稱為a的一個反元．不難驗證，如果元素a有一個反元，那么這個反元是唯一的，a的反元記為-a．設a，b∈R，且b是可反元，我們定義a-b=a+(-b)．不難驗證，對于半環R中的任意元a，b，如果b是可反元，那么a(-b)=-ab，(-b)a=-ba．顯然，一個半環R是一個環當且僅當R的每一個元都是可反元；R是零和自由半環當且僅當R中只有零元是可反元．

半環是相當豐富的．例如，每一個帶有單位元的環是一個半環；每一個布爾代數、每一個有界分配格都是半環，并且是零和自由的；整數環Z(有理數域Q，實數域R)的正錐Z0(Q0，R0)是一個零和自由半環；Max-Plus代數(R∪{-∞}，max，+)是一個零和自由半環．

(a)r(m+m′)=rm+rm′；

(b) (r+r′)m=rm+r′m；

(c) (rr′)m=r(r′m)；

(d) 1Rm=m；

(e)r0=0=0m．

類似地，可定義半環S的右S-半模．一個交換幺半群(M，+)如果既是左R-半模又是右S-半模，并且?a∈R，m∈M，b∈S，均有(am)b=a(mb)，則稱M為(R，S)-雙半模．

注1如果φ是半環R到S的一個同構映射(或反同構映射)，那么φ(0)=0，φ(1R)=1S．

定義6設R，S是兩個半環，M是(R，S)-雙半模，則集合

在通常的矩陣加法和乘法下構成一個半環，稱之為形式三角矩陣半環．

注2在定義6中，當R，S是環時，半環Tri(R，M，S)就是形式三角矩陣環[16]．

(1)

證充分性 通過直接驗證可得φ是半環Tri(R，M，S)的一個自同構．

必要性 設φ是半環Tri(R，M，S)的任一自同構．對于任意X，Y∈Tri(R，M，S)，設

則有

再設

那么，由

φ(X+Y)=φ(X)+φ(Y)φ(XY)=φ(X)φ(Y)

得

(2)

(3)

下面分3步來完成必要性的證明．

步驟1證明φ11(1R，0，0)=1R，φ11(0，0，1S)=0，φ22(1R，0，0)=0，φ22(0，0，1S)=1S，f12(1R，0，0)是M中的可反元．

用φ作用于

可得

(4)

所以

φ11(1R，0，0)=φ11(1R，0，0)2φ22(1R，0，0)=φ22(1R，0，0)2

由于半環R，S的冪等元都是平凡的，所以φ11(1R，0，0)=0或φ11(1R，0，0)=1R，φ22(1R，0，0)=0或φ22(1R，0，0)=1S．

如果φ11(1R，0，0)=0，φ22(1R，0，0)=1S，那么由(4)式，得

(5)

(6)

比較(5)式與(6)式，得

φ22(1R，m，s)=1S

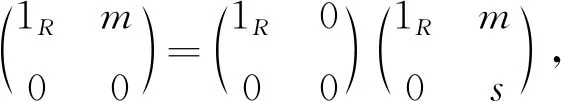
(7)

比較(5)式與(7)式，得

這與φ是半環Tri(R，M，S)的自同構相矛盾．

因此φ11(1R，0，0)=1R．于是

類似可證φ22(0，0，1S)=1S，于是

于是

φ11(0，0，1S)=0φ22(1R，0，0)=0f12(0，0，1S)+f12(1R，0，0)=0

設f12(1R，0，0)=m0，則m0是M中的可反元，并且f12(0，0，1S)=-m0．

步驟2證明分別存在半環R，S的自同構φR，φS，使得對于任意r∈R，m∈M，s∈S，均有

φ11(r，m，s)=φR(r)φ22(r，m，s)=φS(s)

φ11(1R，0，0)=1Rφ22(1R，0，0)=0f12(1R，0，0)=m0

可得

所以

φ11(r，0，0)=φ11(r，m，s)φ22(r，0，0)=0

f12(r，0，0)=φ11(r，m，s)m0

類似可證

φ22(0，0，s)=φ22(r，m，s)，f12(0，0，s)=-m0φ22(r，m，s)，φ11(0，0，s)=0

從φ11(r，0，0)=φ11(r，m，s)，φ22(0，0，s)=φ22(r，m，s)看出，φ11(r，m，s)與m，s無關，φ22(r，m，s)與r，m無關．

f12(r，0，0)=φR(r)m0f12(0，0，s)=-m0φS(s)

(8)

由(2)式與(3)式，得

φR(r+r′)=φR(r)+φR(r′)φS(s+s′)=φS(s)+φS(s′)

φR(rr′)=φR(r)φR(r′)φS(ss′)=φS(s)φS(s′)

對于任意r，r′∈R，當r≠r′時，有

即

那么φR(r)≠φR(r′)，所以φR是單射．

步驟3證明存在(R，S)-雙半模M的一個(φR，φS)-半線性自同構f，使得對于任意r∈R，m∈M，s∈S，均有

f12(r，m，s)=φR(r)m0-m0φS(s)+f(m)

由(2)式和(8)式，得

f12(r，m，s)=f12(r，0，0)+f12(0，m，0)+f12(0，0，s)=φR(r)m0-m0φS(s)+f12(0，m，0)

下證f是M的一個(φR，φS)-半線性自同構．

用φ作用于等式

得

f(m+m′)=f(m)+f(m′)

再用φ作用于等式

得

f(rms)=φR(r)f(m)φS(s)

對于任意m，m′∈M，當m≠m′時，有

即

由此可得

φR(r)=0φS(s)=0f(m)=m′

所以f是滿射，從而f為(R，S)-雙半模M的一個(φR，φR)-半線性自同構．

綜上所述，必要性得證．

注3在定理1中，當R，S是兩個環，M為(R，S)-雙模時，可得文獻[12]的定理2．

(9)

證類似于定理1，從略．

注4在定理2中，當R=S是環，M為(R，S)-雙模時，可得文獻[13]的定理．

定義7設M是一個半模．如果?m，m′∈M，由m+m′=0可推出m=m′=0，則稱M為零和自由半模．

由定義7知，一個半模M是零和自由的當且僅當M只有零元是可反元．

由定理1和定理2得：

定理3設R，S是兩個半環，并且所有冪等元是平凡的，M為非零的(R，S)-雙半模，且是零和自由的，φ是形式三角矩陣半環Tri(R，M，S)到自身的一個映射．那么

(10)

(11)